几种滤波算法的分析与比较

陈菘 卢敏

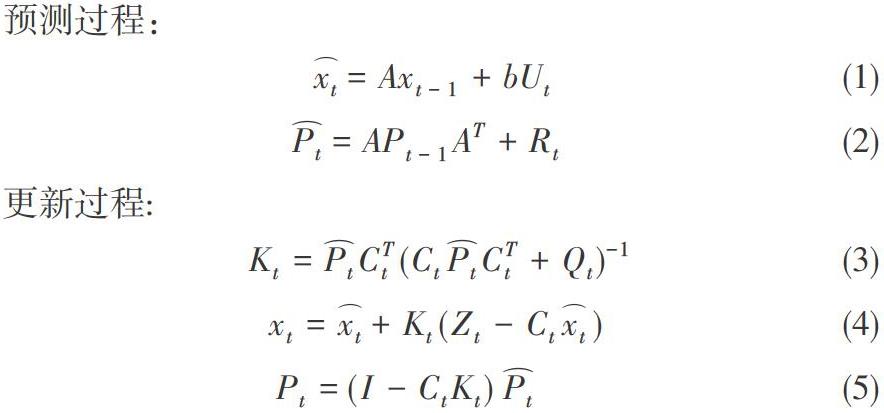
摘要：滤波算法常用来解决对系统状态估计的问题，主要有卡尔曼滤波、粒子滤波以及在此基础上改进的扩展卡尔曼，无迹卡尔曼，无迹粒子滤波算法等。对于线性高斯系统模型，卡尔曼滤波有着极强的处理能力，因此得到了广泛的应用。粒子滤波无须对系统状态做线性高斯假设，其应用范围大于卡尔曼滤波，但时间的消耗要远远大于前者。在介绍了常见滤波算法的原理与应用后，通过仿真实验对比了上述几种常见滤波方法的跟踪效果。实验表明，上述算法在非线性高斯模型下均有较好的准确性与较低的误差。

关键词：卡尔曼滤波;扩展卡尔曼滤波;无迹卡尔曼滤波;粒子滤波;高斯噪声

中图分类号：TP391.9    文献标识码：A

文章编号：1009-3044（2020）32-0023-03

Abstract： Filtering is used to estimate the system state， including Kalman filter（KF）， particle filter and  extended kalman（EK）， unscented kalman（UK）， unscented particle filter algorithm. For linear Gaussian system， Kalman filter has a strong processing ability， so it has been widely used in the field. Linear and Gaussian assumption is not necessary in particle filter contrast to KF， the application range is larger than t-he latter and the time consumption is stronger than the latter. introducing the principle a=nd application of filtering algorithms， the tracking effect are compared through simulation experiments. Experimental resultsshows that improved algorithm have better accuracy and lower error in the model of nonlinear gaussian.

Key words： kalman filter; extended KF; unscented KF; particle filter; gaussian noise

1 引言

滤波问题是求解感兴趣分布的后验概率分布[1]。求解后验概率分布问题有两种方法，第一种是基于贝叶斯理论求解出具体的解析解，贝叶斯滤波通过结合先验概率密度与观测似然函数来求解估计问题[2]。这一方法主要包括卡爾曼滤波、扩展卡尔曼滤波。第二种方法是基于蒙特卡罗与大数定理的思想从原分布中采样从而估计系统真实的状态[3]。蒙特卡罗思想指的是用一系列抽样样本值模拟原分布。这一方法主要包括无迹卡尔曼滤波与粒子滤波[4]。表1是上述几种滤波方法应用条件的对比。

由表1可得，卡尔曼滤波只能应用在线性高斯过程中，其改进方法扩展卡尔曼滤波与无迹卡尔曼滤波对非高斯噪声有一定的处理能力，但是三者均不能很好地处理非线性系统。无论系统线性与否，噪声是否服从高斯分布，粒子滤波均可以处理，因此粒子滤波算法获得了广泛的应用。

2 卡尔曼滤波及其变形

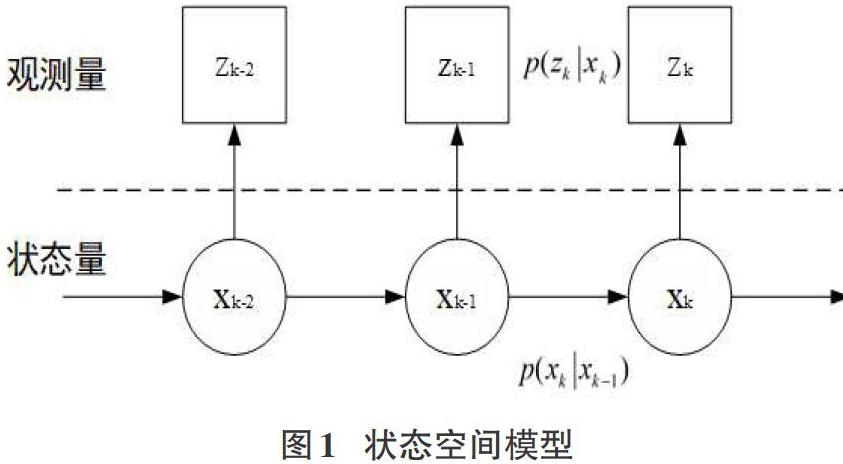
状态模型由状态转移过程和观测过程两部分组成，如图1所示。

应用这个模型有两个前提：（1）观测独立假设[5]，系统当前的观测量只与当前时刻的状态量有关，与其余时刻的状态无关;（2）一阶马尔可夫过程[6]，即系统当前时刻的状态量只与上一个时刻的状态量有关，与其余时刻的状态量无关。

2.1 卡尔曼滤波

卡尔曼滤波的状态方程与观测方程必须是线性的，即图1中的[xk-2，xk-1，...zk-2，zk-1]是线性关系。即状态量之间的关系，状态量与观测量之间的关系可以用矩阵来表示。同时，观测噪声与状态噪声的统计分布须满足高斯分布。在这两个前提下，图1所表示的状态空间模型可以使用卡尔曼滤波算法来处理。卡尔曼滤波由预测和更新两个步骤构成，预测是根据系统上一时刻的状态预测系统下一时刻的状态，更新则是结合最新的观测值数据对预测的状态值进行修正从而得到系统的估计值。

式（1）到（5）中，[xt]表示状态的预测量，[xt]表示真实的状态量，[Ut]表示控制量[7]，[Pt]表示预测误差的估计值，[Rt]表示过程噪声，[Kt]表示卡尔曼增益，[A]表示状态转移矩阵，[Zt]表示观测值，[Pt]表示预测误差的真实值，[Q]表示观测噪声。

2.2 扩展卡尔曼滤波

当系统不满足线性条件约束时，即状态量与状态量，状态量与观测量之间无法用矩阵关系表达，但过程噪声与观测噪声仍满足高斯分布时，此时可通过泰勒公式近似某点处的状态方程实现非线性方程的线性化，同时为了避免计算的复杂性，扩展卡尔曼滤波只近似到泰勒方程的一阶项[8]。由于忽略了高阶项，不可避免地引入了误差，当非线性过强时，往往估计的效果比较差，甚至可能导致发散。在扩展卡尔曼滤波过程中，状态转移矩阵[A]与观测矩阵[Z]要通过计算雅克比矩阵与海塞矩阵得到。因此，相比卡尔滤波，增加了计算的复杂度。

2.3 无迹卡尔曼滤波

无迹卡尔曼滤波引入了无迹变换。对于非线性模型，直接用解析的方式来求解贝叶斯递推公式比较困难，各个概率分布的均值和方差比较难求，无迹变换通过一定规律的采样并赋予采样值权重近似获得均值与方差。通过无迹变换近似值得到的估计状态精度相当于二阶扩展卡尔曼的精度。

3 粒子滤波及其变形

3.1 粒子滤波

粒子滤波是基于蒙特卡罗仿真的递归贝叶斯算法，通过从后验概率密度中采样对状态进行数值求解。粒子滤波将状态矢量表示为一组带有权值的随机样本，并且基于这些样本和权值可以计算出状态估值。该方法没有线性模型与高斯噪声的限制，因此可以处理用任何状态模型描述的系统。但粒子滤波多次迭代后权值高度集中，导致了粒子退化，针对粒子退化的问题，可以采用重采样的方法来解决，重采样过程主要有多项式重采样，系统重采样[9]，即复制权重大的粒子，并用这些粒子替代小权重粒子。粒子滤波的过程如表2所示。

3.2 扩展卡尔曼粒子滤波

擴展卡尔曼滤波是一种局部线性化的方法，它通过一阶泰勒展开式实现。由于使用了扩展卡尔滤波，系统噪声须满足高斯分布。

扩展卡尔曼结合粒子滤波思路如下：在采样阶段，利用扩展卡尔曼滤波为每个粒子计算均值与协方差，然后利用均值与协方差信息进行采样。在扩展卡尔曼滤波计算均值与方差的过程中利用到了最新时刻的观测值数据，因此，相比基本的粒子滤波算法，估计的精度有了一定程度的提高。

3.3 无迹粒子滤波

无迹粒子滤波是一种递归的最小均方误差估计。与基本的粒子滤波算法相比，无迹粒子滤波在计算均值与方差的过程中利用到了最新的观测信息[Zk]，因此估计的精度要优于粒子滤波算法。与扩展卡尔曼粒子滤波相比，通过使用无迹变换，后验方差与均值的估计能够精确到二阶及以上，因此估计精度也要优于扩展卡尔曼粒子滤波。

4 仿真

本实验中所采用的非线性观测模型与量测模型来自文献[10]，如下所示：

图2与图3的跟踪时长设置为50，过程噪声方差为3，观测噪声方差为1，采样的粒子数目为100。由图2可知，扩展卡尔曼滤波（EKF）、无迹卡尔曼滤波（UKF）、粒子滤波（PF）、扩展卡尔曼粒子滤波（EPF）、无迹粒子滤波（UPF）均有比较好的跟踪精度，大部分时段的估计状态与真实状态相接近，EKF在3时刻有一个较大的误差出现。由图3可知，在上述几种滤波方式中，UPF的误差在整个跟踪过程中都比较小，大部分时间都接近于0，说明UPF的误差稳定性优于其他的滤波方式。EKF与PF的误差起伏比较大，误差的稳定性不如其他的滤波方式，但是总体的误差水平也比较小。通过对比图2与图3，可以得出EKF，UKF与PF，EPF，UPF在该模型下有着较好的跟踪效果与较小的误差。

5 结论

本文首先对卡尔曼滤波、粒子滤波及基于前者改进的滤波算法进行了理论介绍，然后通过仿真实验对比了扩展卡尔曼滤波、无迹卡尔曼滤波、粒子滤波、扩展卡尔曼粒子滤波、无迹粒子滤波算法的跟踪效果与误差，得出在非线性高斯模型下卡尔曼滤波算法与粒子滤波算法均能达到比较好的估计效果，估计值与状态真实值比较接近。下一步将研究这些滤波算法在具体场景中的应用。

参考文献：

[1] 苏续军，吕学志.基于贝叶斯推断的复杂系统可靠性分析[J].计算机应用与软件，2019，36（3）：219-226，294.

[2] 黄小平，王岩，缪鹏程.粒子滤波原理及应用：MATLAB仿真[M].北京：电子工业出版社，2017.

[3] 王法胜，鲁明羽，赵清杰，等.粒子滤波算法[J].计算机学报，2014，37（8）：1679-1694.

[4] 乔少杰，韩楠，朱新文，等.基于卡尔曼滤波的动态轨迹预测算法[J].电子学报，2018，46（2）：418-423.

[5] 孟庆旭.粒子滤波算法研究及其在非线性估计中的应用[D].武汉：华中科技大学，2019.

[6] 董俊松.基于扩展卡尔曼滤波的单目标跟踪算法研究[D].兰州：西北师范大学，2019.

[7] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].2版.西安：西北工业大学出版社，2012.

[8] 周雪，张皓，王祝萍.扩展卡尔曼滤波在受到恶意攻击系统中的状态估计[J].自动化学报，2020，46（1）：38-46.

[9] 冯驰，吕晓凤，汲清波.粒子滤波理论及其在目标跟踪中的应用[J].计算机工程与应用，2008，44（6）：246-248.

[10] 王航星，潘巍.基于自适应吸引半径的萤火虫算法的粒子滤波[J].计算机应用研究，2019，36（12）：3632-3636.

【通联编辑：梁书】