一种改进的锁相环用于抑制三相不平衡和直流偏移

杨旭红， 郝鹏飞， 姚凤军， 陆 浩

(上海电力大学自动化工程学院， 上海 200090)

近年来，中国新能源发电(如太阳能、风能)大规模发展，为了实现逆变器高效高质量的并网，通常采用锁相环对电网基波分量的相位和频率进行锁相，达到与电网同步[1-2]。

目前，中外学者已对锁相环开展了大量研究。文献[3]提出了同步参考系锁相环(synchronous reference system phase-locked loop,SRF-PLL)，在理想电压下，对相位和频率可快速、精确地锁定，但在电网电压畸变以及存在谐波等不平衡情况下，SRF-PLL不能准确地进行锁相，影响逆变器并网性能。针对此缺陷，文献[4]提出了一种基于双二阶广义积分器锁相环的设计方法，解决了在电网电压三相不平衡下锁相失败的问题，但是在电网含高次谐波的时候，检测到的相位和频率存在很大的波动。文献[5]对双二阶广义积分器锁相环进行了改进，引入了一个调节参数，虽然能够抑制直流偏移，提高锁相精度，但是对该参数的依赖性较高。文献[6-7]提出了解耦双同步参考坐标系锁相环(DDSRF-PLL)，在不平衡三相系统中实现了正、负序电压的解耦，消除了负序电压对锁相的影响，但当电网存在直流偏移时，锁相精度不够高。文献[8-9]提出了基于二阶广义积分器的双同步解耦坐标系锁相环，同时消除了谐波和电压不平衡以及畸变带来的影响，提高了锁相的快速性和精准性，但锁相环设计还面临一个主要问题，就是直流偏移给频率和相位估计带来的误差，上述研究没有将其考虑在内。为此，文献[10]提出了基于带通滤波器(bandpass filter, BPF)的锁相环技术方法，在电网电压含直流偏移时具有比较好的锁相效果。文献[11]为消除直流偏移对锁相环性能的影响，采用自适应最小均方算法对电网电压中的直流偏移分量进行滤除，但是，算法复杂，计算量较大。文献[12]提出一种基于复变陷波器的直流分量抑制方法(direct current offset rejection method using complex notch filter, DCCNF)，能够完全消除直流分量造成的影响，且具有较好的动态性能，但是对谐波比较敏感。

为了提高复杂电网情况下锁相的整体性能，提出基于混合二阶和三阶广义积分器正交信号发生器(MSTOGI-QSG)的改进型DDSRF-PLL结构，主要利用混合二阶和三阶广义积分器良好的滤波器能力，实现对谐波和直流偏置分量的滤除。同时，基于解耦双同步参考系锁相环，加入非线性函数来调整PI控制器的参数，快速准确跟踪电网电压，提高对电网基波电压频率和相位检测的精确性[13]。

1 解耦双同步参考系锁相环

如图1所示，解耦双同步参考系锁相环结构中含有两个旋转坐标系，正、负序坐标分别以角速度ω和-ω沿逆时针方向和顺时针方向旋转，角度分别为θ和-θ。

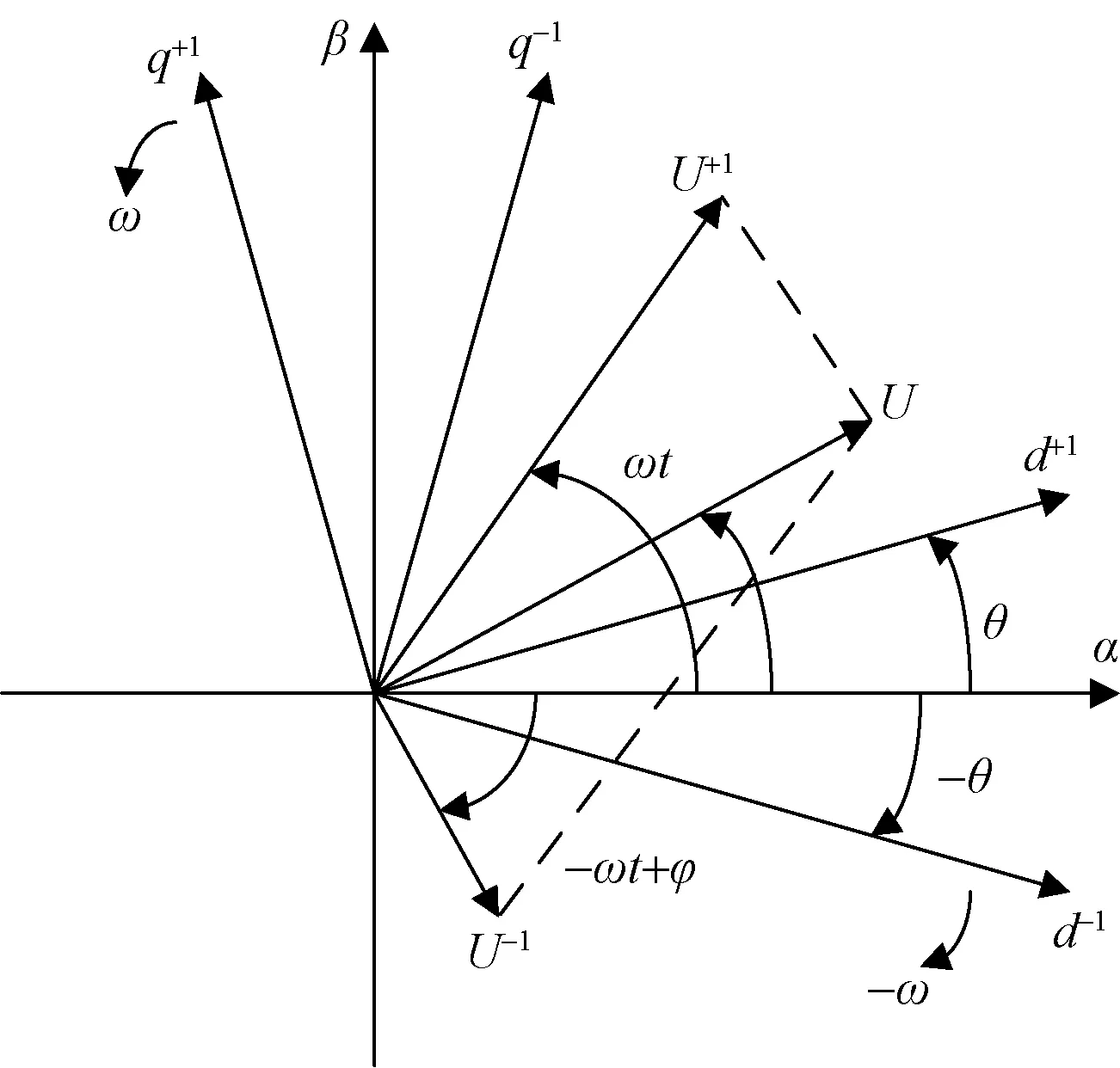
d+1q+1、d-1q-1分别为正序和负序dq轴坐标； ω为电网电压基波角频率；φ为初始相位；θ为角度估计； U为电压模值，U+1、U-1分别为正、负序电压幅值分量图1 双同步参考系电压矢量图Fig.1 The diagram of double synchronous reference frame voltage vector

dq坐标系下正负序电压udq+1和udq-1分量分别为

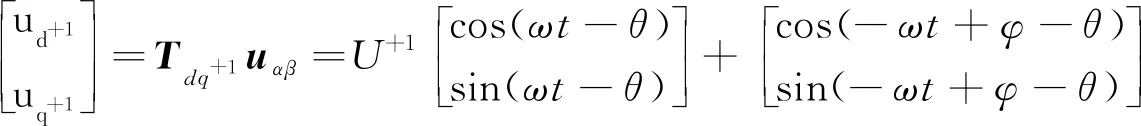
(1)

(2)

式中：ud、uq分别为d轴和q轴电压分量；+1，-1分别表示正负序；Tdq为αβ坐标轴到dq坐标轴转换矩阵。

正负序矩阵关系为

在PLL中适当调整PI控制器参数可实现θ=ωt，假设：

(3)

在式(3)假设条件下，式(1)、式(2)化简为

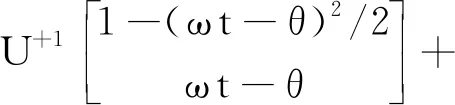
(4)

(5)

从式(4)、式(5)不难看出，正、负序分量都含2次谐波，且存在耦合，所以当电压不平衡时，由于负序分量的存在，会造成锁相误差，可以通过解耦网络来得到抑制。假设任一个输入电压Uαβ由正、负序分量构成，分别以角速度+ω和-ω旋转。

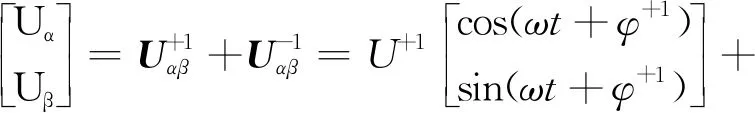
(6)

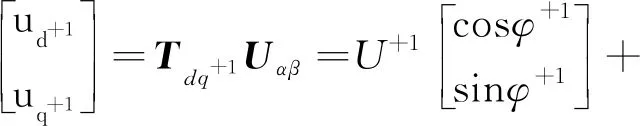
(7)

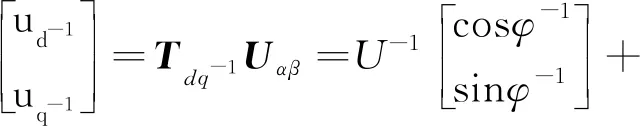
(8)

由式(7)、式(8)可知，dq坐标系下正负序电压存在耦合，为了消除负序分量的影响，故而引入解耦网络，如图2所示。图3中n=+1，m=-1(分别代表正、负序)实现正、负序电压解耦。

DDSRF-PLL整体控制结构如图3所示，在电网三相电压不平衡的情况下，该方法可有效分离正序分量中的负序分量，提取基波正序分量，完成锁相。但是，在高畸变率的三相不平衡电压下，DDSRF-PLL检测到的相位和频率畸变严重且存在严重的振荡。为解决这个问题，需要在两相静止坐标系上加入额外的滤波器以消除谐波和直流偏置分量的影响，提高锁相精度。

2 基于混合二阶和三阶广义积分器的滤波器

二阶广义积分器(SOGI)可以有效地滤除电压中的谐波，已被广泛应用于并网逆变器实现电网同步。然而，如果电网电压中存在直流偏置分量，那么

为正序d、q轴电压；为解耦后正序 d、q轴电压；为解耦后经过滤波的负序电压图2 正序解耦单元Fig.2 The decoupled unit ofpositive sequence

为负序d、q轴电压；为解耦后负序 d、q轴电压；为解耦后经过滤波的正序电压； f、θ分别为输出频率和相位，LPF为低通滤波器图3 DDSRF-PLL模型Fig.3 Block diagram of DDSRF-PLL

传统的SOGI的性能就会受到直流偏置分量影响。为此，采用二阶和三阶混合广义积分器正交信号发生器(MSTOGI-QSG)，结构如图4所示，以消除电网电压直流偏置引起的这种影响。MSTOGI-QSG是在传统SOGI上增加了一条积分回路以消除直流分量。

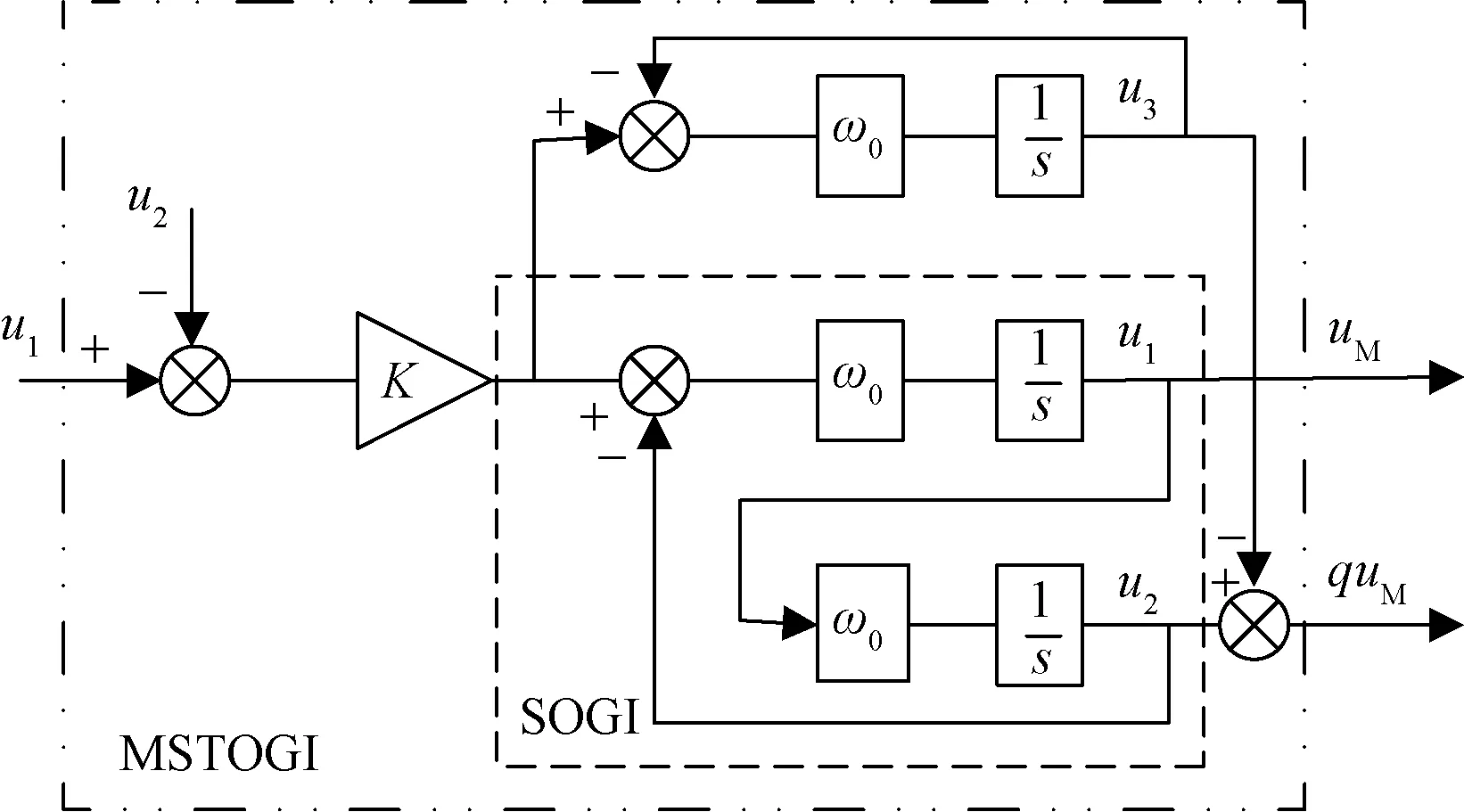
u、ω0、k分别为输入信号、谐振角频率、阻尼因子；u1、u2、u3为 SOGI输出正交信号；u3为增加的积分回路的输出；uM和quM分别 表示 MSTOGI-QSG 的正交输出电压图4 MSTOGI-QSG结构图Fig.4 Block diagram of the MSTOGI-PLL

由图4得MSTOGI-QSG的闭环传递函数:

(9)

(10)

(11)

(12)

式中：G1(s)和G2(s)为SOGI的闭环传递函数；G3(s)为增加的积分回路的闭环传递函数，将这条积分回路的输出连接到u2上，此时，得到MSTOGI的两个闭环传递函数G1(s)和G4(s)。由文献[14]可知，要使正交信号发生器能够滤除谐波和直流偏移分量，闭环传递函数应为带通滤波器。由式(8)、式(9)可知，G1(s)是二阶带通滤波器，可以滤除直流分量，而G2(s)是二阶低通滤波器，一旦u包含任何DC偏置分量，u2就会产生带k增益的DC偏移，从而导致u的幅值检测出现误差，同时也会影响PLL跟踪电网电压。所以SOGI不能够有效地消除直流偏移的影响。由式(11)可知，G4(s)是带通滤波器，故采用的混合二阶和三阶广义积分正交信号发生器(MSTOGI-QSG)可以有效滤除谐波和直流偏移。

图5、图6为具有不同阻尼因子(k)的G1(s)和G4(s)的伯德图，其中当谐振角频率(ω0)等于电网角频率(ωs)时，从图5可以清楚地看到，G1(s)在谐振角频率(ω0)处具有单位增益和零相移，G4(s)在谐振角频率(ω0)处具有与G1(s)相似的性质，并且uM和quM正交。此外，G4(s)在低频带和高频带中都具有较大的衰减，这可以有效消除输入信号存在的直流偏移和高频谐波。当谐振角频率(ω0)不等于电网角频率(ωs)时，G1(s)和G4(s)均与阻尼因子(k)有关系，由图5、图6分析可知，取k=1.414。

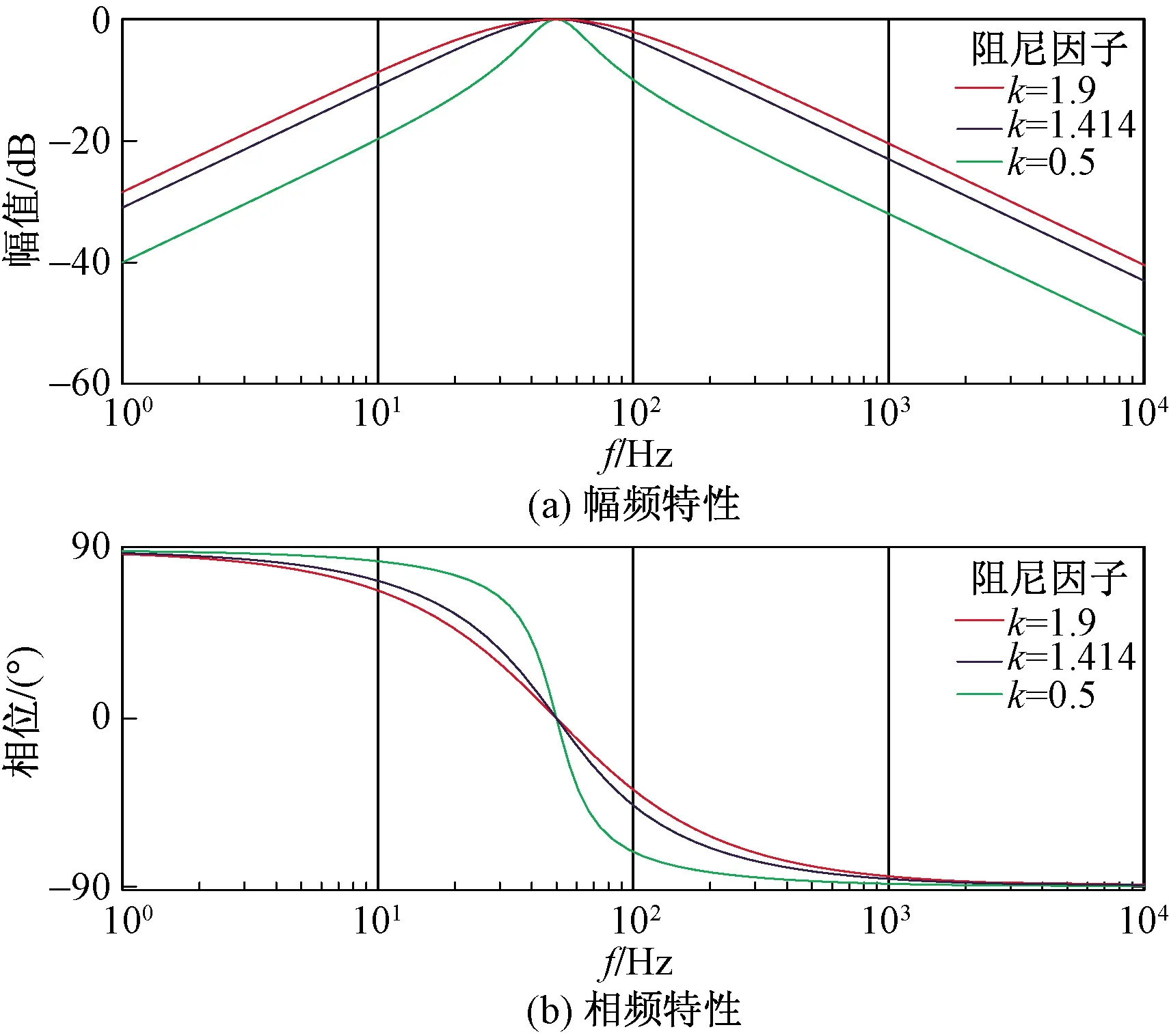
图5 不同k值下传递函数G1(s)的伯德图Fig.5 Bode plot of G1(s) with different k values.

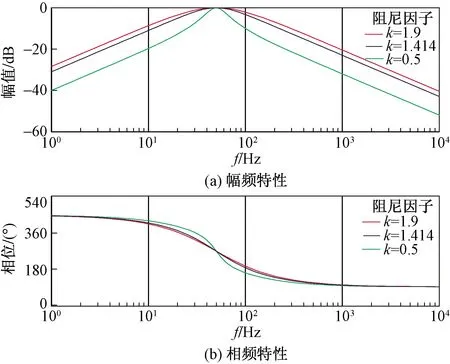
图6 不同k值下传递函数G4(s)的伯德图Fig.6 Bode plot of G4(s) with different k values.

3 基于MSTOGI-QSG的DDSRF-PLL

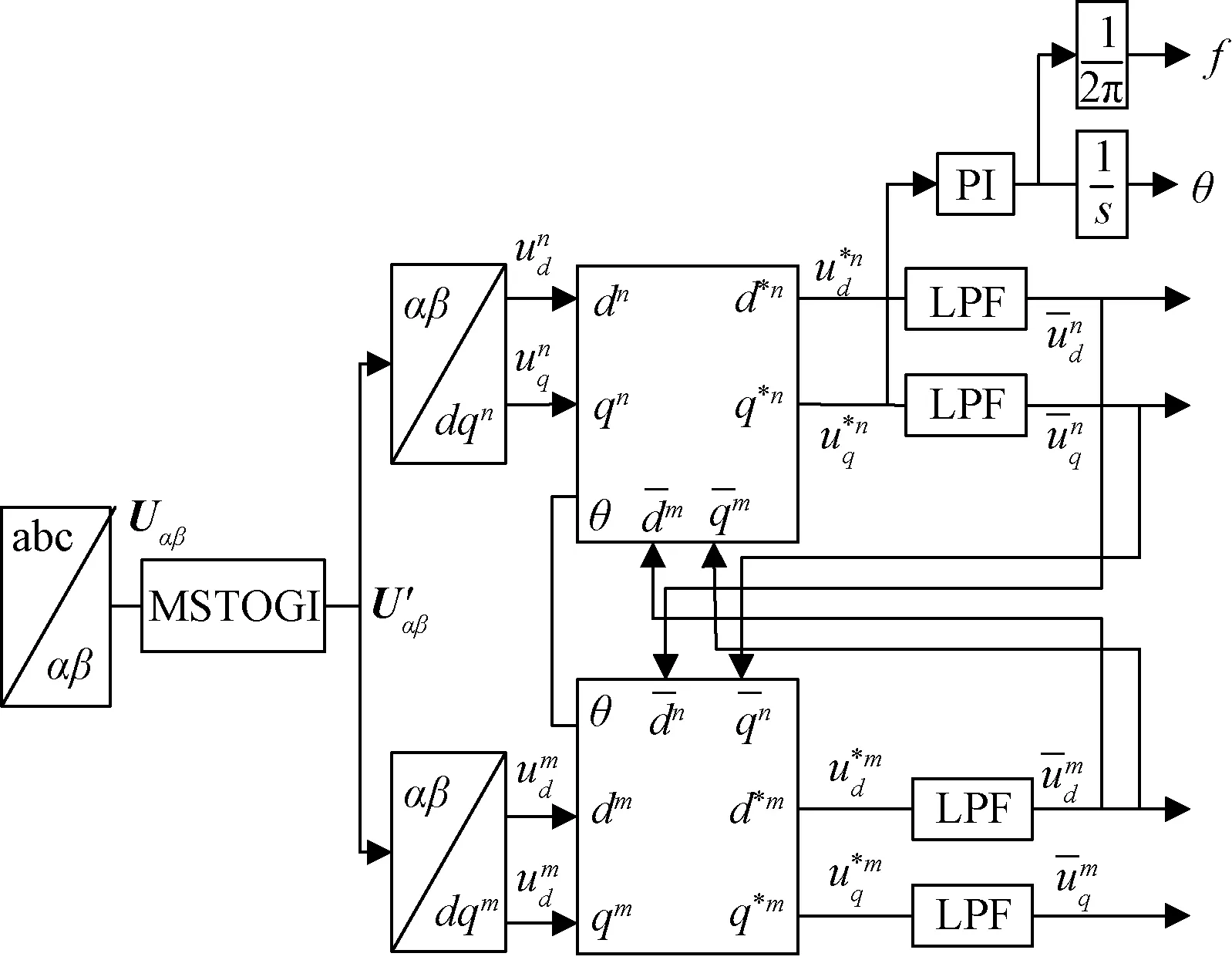
图7 提出的改进锁相环结构Fig.7 Block diagram of improved phase-locked loop

如图7所示,改进的锁相环结构是在DDSRF-PLL前增加了两个MSTOGI，整个锁相环原理为：三相电压经过Clark变换得到两相静止坐标系下电压矢量uαβ，然后经过MSTOGI对多次谐波和直流偏置分量进行滤波，得到稳定的电压信号u′αβ，再通过park变换得到两相旋转坐标系下电压信号，经正负序解耦网络进行正负序提取和分离，最后将正序电压引入PLL完成锁相。

4 非线性PI控制器设计

电网的实际运行状况比较复杂，而对锁相的速度与精度要求较高，传统的PI控制很难满足电网的实际运行状况，故而，引入非线性PI控制器。图8为系统的阶跃响应曲线，据此，利用反馈误差与时间的关系设计比例系数和积分系数。

图8 系统阶跃响应Fig.8 Step response of system

4.1 比例系数(kp)的设计

在响应时间[0t1]段，为了使系统有快的响应速度，比例系数(kp)在初始时刻应较大，但为了减小超调，使误差e较小，故比例系数随之减小；在[t1t2]段，为了增大系统反向控制作用，同时有小的超调，kp应逐渐增大；在[t2t3]段，为了使系统尽快达到稳定状态，且不再产生较大的惯性，kp应逐渐减小；在[t3t4]段，kp应逐渐增大，作用与[t1t2]段相同。根据上述变化规律，kp随误差(e)的变化趋势如图9所示，构造非线性函数为

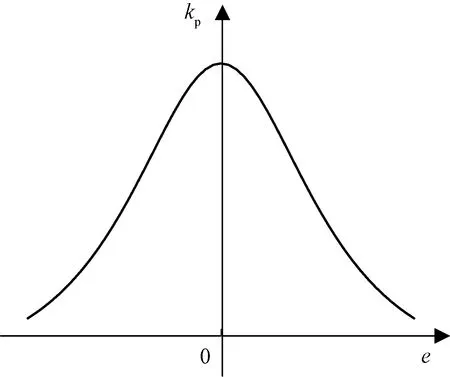
图9 kp随误差变化曲线Fig.9 kp curves with error variation

kp[e(t)]=ap+bp{1-sech[cpe(t)]}

(13)

式(13)中：sech为双曲正割函数；ap、bp、cp为正实常数；当e趋向于无穷大时，kp取得最大值ap+bp；当e等于零，kp为最小值ap；bp为kp的变化区间，调整bp的区间范围可以改变kp的变化速率。

4.2 积分系数(ki)的设计

当误差信号e较大时，为了防止响应产生严重震荡，同时保持小的超调量，积分系数不应该太大；当误差信号e较小时，应该增大积分系数，以消除系统的误差。根据上述变化规律，积分系数ki随误差e的变化趋势如图10所示。构造非线性函数为

ki[e(t)]=aisech[cie(t)]

(14)

式(14)中：ai、ci为正实常数；ki取值为(0，ai)，当e等于零时，ki取最大值ai；通过改变ci的大小可调整ki的变化速率。非线性PI控制器的控制输入为

(15)

为了得到比常规PI控制更快的响应速度与更小的超调，通过恰当设计非线性函数的参数，达到电网电压在不同运行状况下能更快、更精确地锁定电网电压相位、频率和幅值。

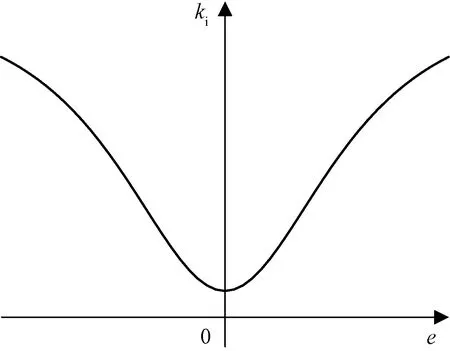
图10 ki随误差变化曲线Fig.10 ki curves with error

5 仿真研究

通过MATLAB/Simulink建立基于MSTOGI的解耦双同步参考系非线性PI控制锁相环的仿真模型，基于MSTOGI的解耦双同步参考系传统PI控制锁相环的仿真模型与传统解耦双同步参考系锁相环的模型，并将它们的仿真结果进行比较。

仿真的主要参数设置为：三相交流电压幅值为1 000 V，频率为50 Hz，传统PI控制器比例参数kp=4，积分参数ki=1，非线性PI控制器参数分别为：ai=132,ci=1,ap=26,bp=8,cp=0.8。

仿真结果如下：方法一为改进的基于MSTOGI的非线性PI控制解耦双同步参考系锁相环，方法二为基于MSTOGI的传统PI解耦双同步参考系锁相环，方法三为传统解耦双同步参考系锁相环。

5.1 电网电压幅值突然跌落

电网电压跌落时仿真波形如图11所示。图11(a)中，三相电网电压a相在0.05 s时跌落50%，其余两相保持不变。由图11(c)可得，在电压骤降后，方法一的频率波动幅度最小，最大幅值也仅为50.013 Hz。方法二为50.021 Hz，方法三为50.041 Hz，而且方法一能够更快地趋于稳定。

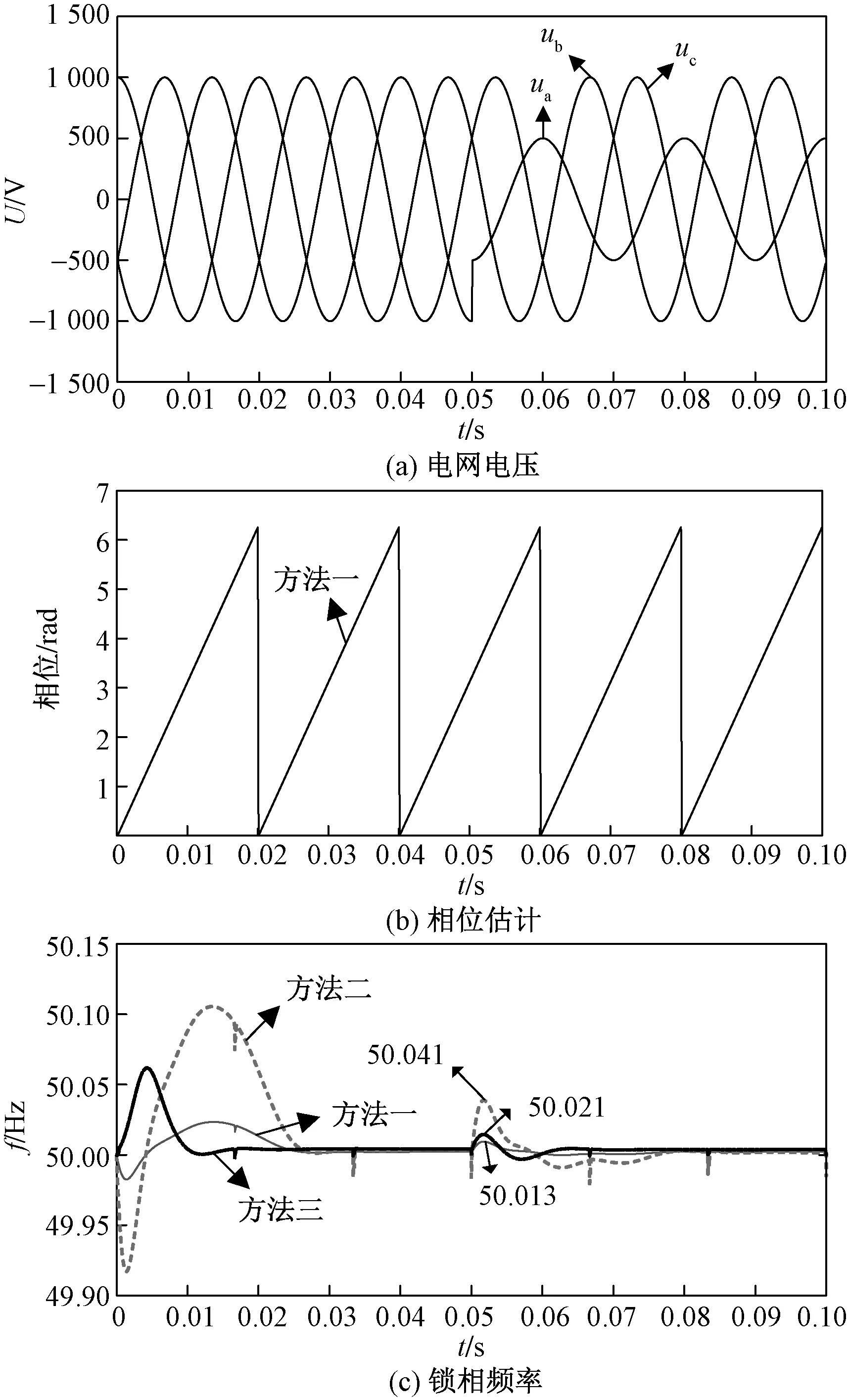
图11 电压幅值突变的仿真波形Fig.11 Simulation waveforms when voltage drops

5.2 含负序电压时仿真波形

含负序电压时的仿真波形如图12所示。图12(a)中，三相电网电压在0.05 s时引入0.2(标幺值)的负序电压，并且基波电压幅值跌落50%。从图12(c)中可以看出，在加入负序电压后，方法三频率振荡最严重，最大幅值为50.14 Hz；方法二最大振荡幅值为50.06 Hz，而方法一最大震荡幅值仅为50.01 Hz,并且在很短的时间内稳定在50 Hz。

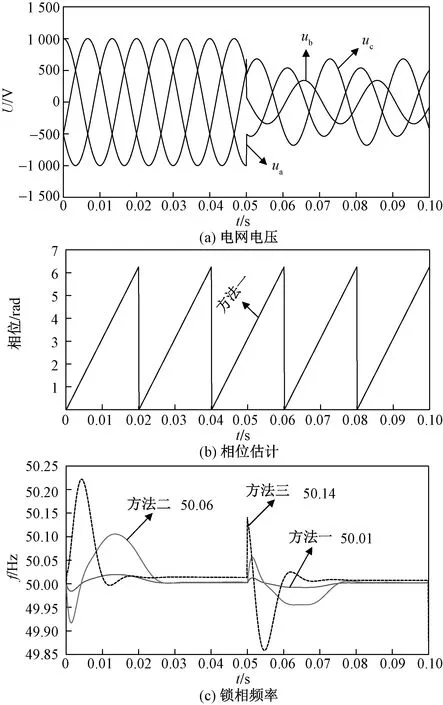
图12 含负序电压的仿真波形Fig.12 Simulation waveforms when negative voltage

5.3 电网电压含有谐波

电网电压含谐波时的仿真波形如图13所示。图13(a)中，三相电网电压a相在0.05 s 时引入0.06(标幺值)的5次谐波，b相引入0.05(标幺值)的7次谐波，并且基波幅值跌落50%。由图13(c)可以看出，方法一的频率振荡最小，最大幅值为50.01 Hz，方法二次之，最大幅值为50.02 Hz，方法三最大，幅值为50.04 Hz。显而易见，方法一最优。

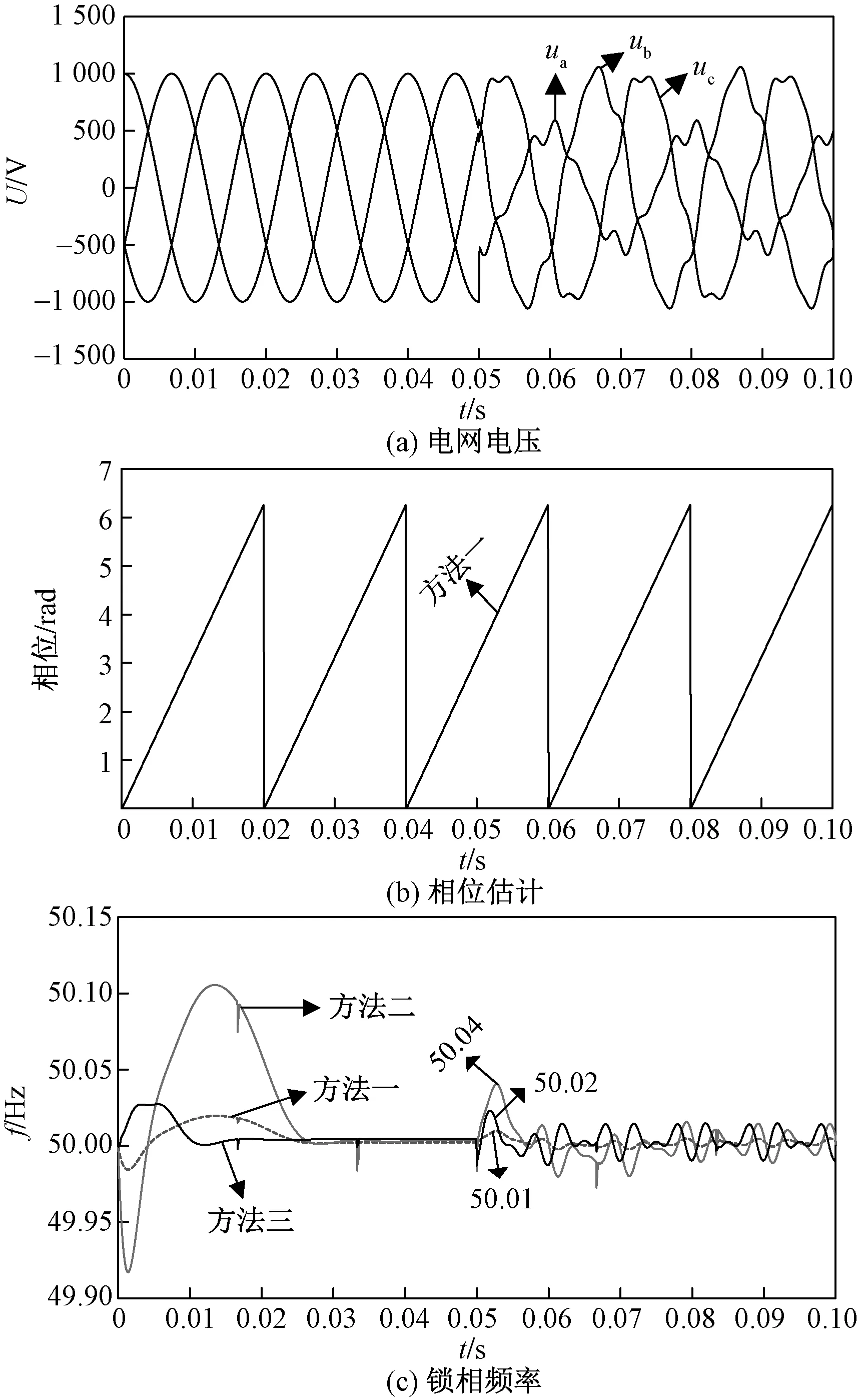
图13 电压含谐波的仿真波形Fig.13 Simulation waveforms with harmonic voltage

5.4 含直流偏移分量

电网电压含直流偏移分量时的仿真波形如图14所示。如图14(a)中所示在0.05 s给a相电压加入100 V的直流偏移分量。由图14(c)可以看出在电网含有直流分量后，较方法一而言，方法二和方法三波动比较大，而且最后频率的稳定值都低于50 Hz，而方法一估计的频率为50 Hz。故而，方法一能够完全消除直流偏置分量的影响，对相位和频率实现精确锁定。

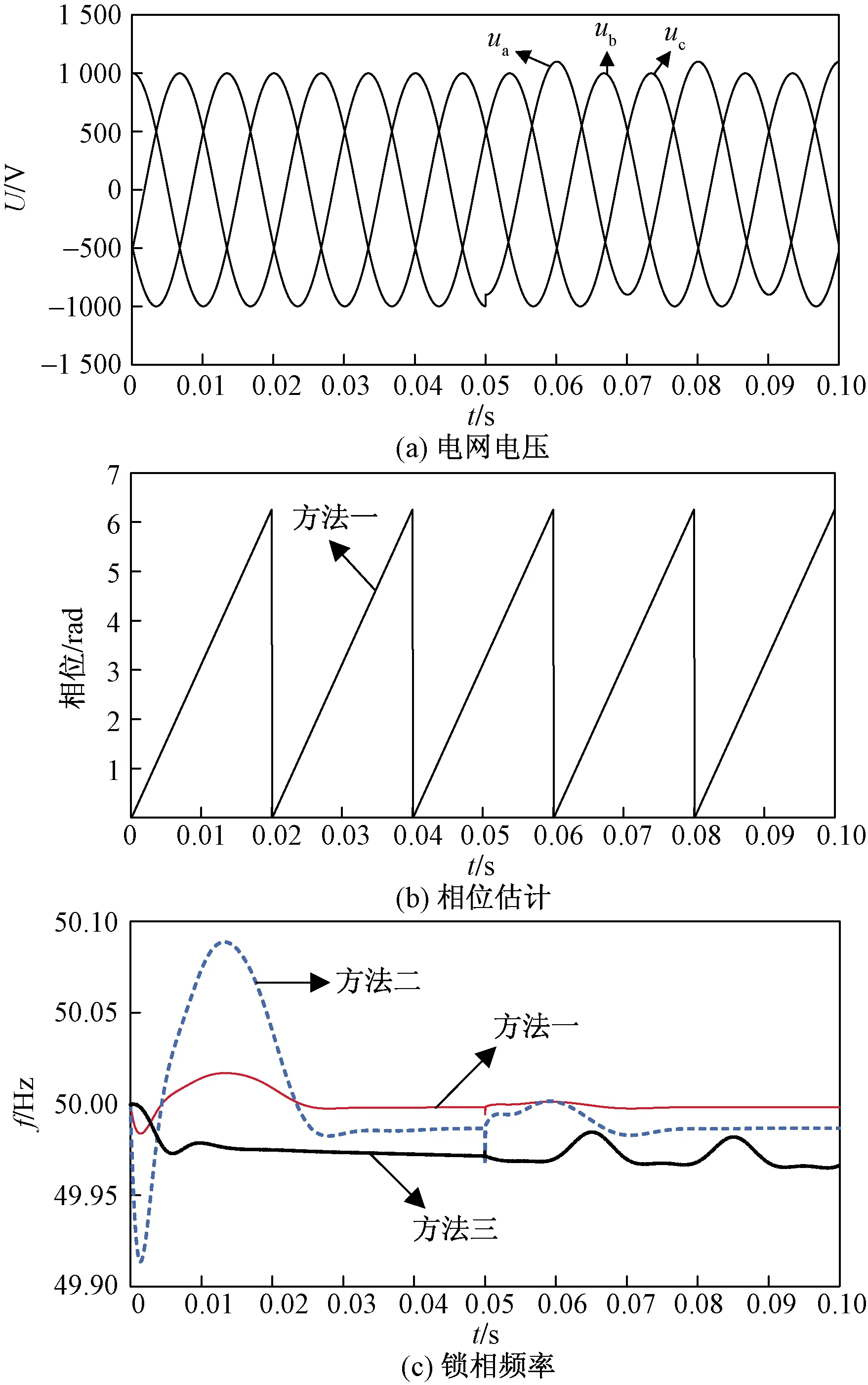
图14 电压含直流偏移的仿真波形Fig.14 Simulation waveform when the voltage contains DC offset

6 结论

分析了DDSRF-PLL的锁相原理，针对DDSRF-PLL在复杂电网电压(三相不平衡、含谐波和直流偏置分量等)情况下检测到的相位频率存在严重畸变和振荡等问题，结合MSTOGI-QSG具有对直流偏移分量和谐波良好的滤波能力，提出了一种基于MSTOGI-QSG的改进DDSRF-PLL设计方法，同时，在PI控制器加入了非线性函数。通过MATLAN/Simulink仿真分析可得到以下结论。

(1)当电网含有谐波和直流偏移，改进的DDSRF-PLL具有良好的抗干扰能力。

(2)当电网电压三相不平衡，改进的DDSRF-PLL能够对相位和频率进行精确地锁定，而且超调更小，达到稳态的时间更短。