计及需求侧响应指标的微电网经济排放调度

张 娟

(东北电力大学电气工程学院，吉林 吉林132012)

近年来，为了能有效缓解能源危机和环境问题，可再生能源发电逐步受到关注[1-2].孤岛微电网由于其独立组网的特点，为高原、海岛等偏远地区分散电力提供了有效的解决方法.然而，由于可再生能源出力的随机性和波动性给电力系统安全运行带来较大挑战[3]，这使得微电网的经济调度难度大大增加，而合理的调度微网内资源将有助于提高微网的运行经济性.因此研究微电网内源储荷协调优化意义重大.传统模式下的微电网大多从供应侧研究能源优化分配，然而随着电能需求的日益增长，负荷峰谷差逐渐被拉大，这使得需求侧响应得到广泛关注[4-5].需求侧响应是指用户根据价格信号或激励机制做出响应，改变其固有用电模式的行为，可分为价格型需求侧响应和激励型需求侧响应[6].伍惠铖等[7]针对含有多个售电商的智能住宅小区，提出了一种考虑负荷转移和多重博弈的智能小区需求侧响应策略，算例结果验证了所提策略可以有效提高系统运行的经济性.罗鑫等[8]为了实现微电网源-网-荷的综合优化，采用混沌烟花算法对微电网中需求侧负荷与电源侧功率进行综合优化，算例结果表明此模型使得微网系统运行的经济性有所提高.陈厚合等[9]综合考虑风电预测误差、负荷波动等因素，将需求侧响应与旋转备用联系起来建立优化模型.刘宝林等[10]提出了一种售电收益最大化和需求侧补偿成本最小化为目标的微电网能量优化调度策略，算例结果表明所提调度策略提高了系统运行的经济型.黄焘等[11]在考虑大电网分时电价的基础上引入需求侧管理，建立了含风光燃储的微电网优化调度模型，降低了用户的购电成本，同时也提高了用户的舒适度.

然而到目前为止，对于需求侧响应的探讨都集中于研究需求侧响应带来的经济优势，但是文献中很少尝试量化需求侧响应的经济效益.Dharme等[12]量化了需求侧响应的经济效益，但是仅仅考虑了单个指数，对于需求侧响应的其他效益并未做出评估.因此，本文在已研究基础上对含风力发电机、光伏发电机、柴油发电机以及蓄电池储能组成的微电网作为研究对象，提出了孤岛微电网的优化调度模型.该模型综合考虑了微电网直接经济成本、需求侧响应成本以及综合碳排放治理成本，同时提出了量化需求侧响应的三个指标，可用于确定特定需求侧响应对于微电网系统的可用性，同时也可以为调度人员工作提供参考依据.最后采用CPLEX对所提模型分别在四种模式下进行算例求解，验证了所提模型的有效性.

1 微电网系统模型

微电网是一个把各个分布式电源及负荷、储能设备结合在一个系统里的小型可控电力系统.一般的微电网系统如图1所示，包括风力发电系统、光伏发电系统、蓄电池储能系统、柴油发电机以及负荷.负荷作为分布式电力系统中的重要组成部分，可分为可控负荷和不可控负荷，不可控负荷为一些基础性用电设备，如照明用电、通信用电等，在调度时段内优先满足其供电；可控负荷为一些用电时段具有一定灵活性的用电设备，如洗衣机、可定时电饭煲等，在调度时段内采用激励型需求响应直接控制方式进行负荷转移，并给予补偿.本文所研究的需求侧响应模型主要是以可控制负荷为研究对象.

1.1 光伏发电模型

光伏发电系统的输出功率与外界的温度Tamb和光照度R有关，关系为[13]

(1)

(2)

在公式(1)和公式(2)中：PPV，STC为标准测试条件下最大功率；RSTC为标准测试条件下光照度值；γ为一个系数；Tr、Ta和TNOC分别为光伏单元的参照温度，光伏单元的实际温度和在正常运行条件下光伏单元的温度.

1.2 风力发电模型

对于风力发电机，风能转化为风机功率输出的能量转换公式为

(3)

公式中：ρ为空气密度；R为风机叶片的半径；V为叶尖来风速度；CP为风能转换效率，是叶尖速比λ与叶片桨距角θ的函数，表达式为

Cp=f(θ，λ).

(4)

叶尖速比λ定义为

(5)

公式中：Ww为风机机械角速度(rad/s).

1.3 柴油发电机模型

柴油发电机的燃料消耗量[14]是其输出功率的线性函数，即

F=F0×Ygen+F1×Pgen，

(6)

公式中：F为燃料消耗率；F0为截距系数；F1为斜率；Ygen为柴油发电机额定功率；Pgen为实际输出功率.

柴油发电机运行功率约束为

(7)

公式中：Lmin为柴油机最小负载率.

此部分中柴油发电机产生的碳排放CO2(Pd)可以表示为[15]

(8)

公式中：a、b和c分别为碳排放系数，它们的值分别设定为28.144 4、1.728和0.001 7.

1.4 蓄电池模型

对容量为Cb额定电压为Ub的单体铅酸蓄电池，假设其允许的最大放电深度为D，放电效率为μb，则每次充放电蓄电池可提供的电能为

Eb=CbUbDμb×10-3.

(9)

一般情况下，蓄电池工作电压稳定，工作电流控制在 0.1 CA 左右，故蓄电池的输出功率为

Pb=CbUb×10-4.

(10)

2 基于低碳效益的微电网调度模型

2.1 微电网运行的低碳综合成本模型

微电网运行的低碳综合成本包括三部分：直接经济成本CZ、需求侧响应成本CX和综合碳排放治理成本CP.

2.1.1 微电网直接经济成本

微电网的直接经济成本包括分布式电源运行成本以及蓄电池储能系统运行成本两部分.

(1)分布式电源运行成本分析

风机、光伏发电系统和柴油发电机的运维成本相似，因为风和光都是清洁能源，不计发电成本，所以风机和光伏发电系统主要考虑设备维护成本，如公式(11)和公式(12)所示.柴油发电机运行需要考虑其发电成本和运维成本两部分，其发电成本与火电机组的发电成本类似，是与其输出功率的二次方相关；其维护成本与风、光发电系统相似，都与输出功率正相关，如公式(13)所示.

Com-pv=Cm-pv·Ppv，t，

(11)

Com-wt=Cm-wt·Pwt，t，

(12)

(13)

公式中：Cm-pv、Cm-wt和Com-de分别为光伏发电单元、风力发电机和柴油发电机的单位功率维护成本；Ppv，t、Pwt，t和Pde，t分别为光伏发电单元、风力发电机和柴油发电机在t时刻输出的额定功率；a、b、c分别为柴油发电机的发电拟合系数.

(2)蓄电池储能系统运行成本分析

蓄电池储能系统的运行维护成本可以分成固定部分和可变部分，前者与蓄电池储能系统的额定容量有关，后者与蓄电池储能系统的累积发电量有关，可表示为：

Com-ess=Cm-ess·Rr-ess+Cme-ess·Ea，

(14)

公式中：Cm-ess·Rr-ess为蓄电池储能系统运维成本的固定部分；Cm-ess、Rr-ess分别为蓄电池储能系统的单位运行维护成本和额定容量；Cme-ess·Ea为蓄电池储能系统的可变运维成本；Cme-ess、Ea分别为蓄电池储能系统的单位运维成本和统计周期内的总充放电电量.

Cz=Com-pv+Com-wt+Cde+Com-ess.

(15)

2.1.2 需求侧响应成本分析

可转移负荷主要是根据供需双方事先签订好的协议，由调度中心向用户发出信号，将用电高峰时期的某些比较灵活的负荷转移到用电低谷期或者新能源出力的高峰期，经过用户的响应之后，主动转移部分负荷，按照协议用户会得到一定的费用补偿，其补偿费用为

(16)

公式中：ρ为可转移负荷的补偿系数；Lin，t为t时刻转入的负荷量；Lout，t为t时刻转出的负荷量.当分布式出力大于负荷的时候，Lin，t0，Lout，t=0；当分布式出力小于负荷的时候，Lout，t0，Lin，t=0.

2.1.3 综合碳排放治理成本分析

柴油发电机发电运行过程中会消耗燃料产生污染气体，例如CO2、SO2、NOx等.为了统计并减少这些气体的排放，就应该减少柴油发电机启动运行，依据不同气体对大气污染的程度不同，从而设置单位气体排放治理费用，类似于罚函数的形式从而产生环境保护成本，表达式如下所示：

(17)

2.2 基于低碳综合成本的微电网调度模型

2.2.1 微电网优化调度的目标函数

微电网利用大量的清洁能源，促进了用电、发电过程的低碳化，根据上文建立的微电网低碳综合成本模型，调度的目标是使低碳综合效益最大，低碳综合成本最小，微电网优化调度的目标函数为

minC1=min(Com-pv+Com-wt+Cd2+Com-ess+CDR+Cpol).

(18)

2.2.2 微电网优化调度模型约束条件

功率平衡约束

PL+Pde+Ppv+Pwt+Pat+Punmet，

(19)

公式中：PL为负荷功率；Punmet为未满足的负荷功率；Pde、Ppv、Pwt、Pbat分别为柴油发电机、光伏、风机和蓄电池功率，其中Pbat为正表示放电，为负表示充电.

设备级约束条件

(1)风机光伏输出功率约束

(20)

公式中：Pwt-max为当前风机最大可输出功率；Ppv-max为当前光伏最大可输出功率.

(2)柴油发电机功率约束

kde-minPde-rate≤Pde≤Pde-rate，

(21)

公式中：Pde-rate为柴油发电机额定功率；kde-min为柴油发电机最小功率比例系数，通常可设为0.3.

(3)蓄电池功率和SOC约束[16]

(22)

公式中：Smax和Smin分别为蓄电池SOC的上下限值；Pmax-charge和Pmax-discharge分别为设定的蓄电池最大充放电功率；η为蓄电池转换效率，充电时取充电效率ηc，放电时取放电效率ηd的倒数1/ηd；Rbat为蓄电池总容量；Δt为时间步长.

系统规划约束条件

(1)可转移负荷的限值约束为

(23)

(24)

(25)

(2)未满足负荷率约束

(26)

公式中：funmet为未满足负荷比例，可用于表征离网型微电网的供电可靠性.离网型微电网未与大电网相连，其负荷需求全部由系统自身独立供应.在进行优化配置时，未满足负荷比例通常小于一定的限值f1.

(3)碳排放约束

为了严格控制碳排放量，减少温室气体的排放，碳排放需要低于碳排的最大值CO2max，即

CO2(Pd)≤CO2max.

(27)

2.3 需求侧响应评价指标

电力需求侧响应是通过改变用户用电方式、提高终端用电效率等手段对终端电能使用进行控制，在满足用户电能使用效用的同时降低电力消耗.微电网优化调度的主要目标是消减高峰负荷同时提高新能源消纳率.因此可以提出三个指标来量化需求侧响应结果.

(1)峰值消减指数

需求侧管理如果合理规划，可以减少一些高峰时段负荷，从而减轻操作员的压力.峰值消减指数可表示为

(28)

公式中：LFDSM是考虑需求侧响应时的电网负载系数，LFWDSM是在没有计及需求响应的情况下运行的电网负载系数.如果需求侧管理成功削减了在高峰时段的负载，峰值功率削减指数会增大.

(29)

(30)

(2)可再生能源消纳率

需求侧管理如果合理规划，可以在可再生能源出力峰值时刻多转移一些负荷来消纳风光等能源，所以可再在能源的消纳率应该会增加.可再生能源消纳率指数Mrei可表示为

(31)

公式中：Pgr为由可再生能源提供的有功功率；Pgt为所有微源提供的有功功率.

(3)用户舒适度

用户各时段的用电量同用户的舒适度密切相关，一般来讲，考虑到用户对电价的自适应性，可以认为，在相对稳定的电价水平下，用户将会自主选择其舒适度最大的用电方式.需求侧响应的投入会改变系统中负荷结构，使用户舒适度降低.因此用户舒适度也是需求侧响应的一个评价指标，其可表示为

(32)

3 算例分析

3.1 算例设置

以某孤岛微网为例，该微网内有2台柴油发电机160 kW，蓄电池容量为800 kW，风电机组装机容量为350 kW，光伏装机容量为250 kW.柴油发电机和可再生能源的功率限值如表1所示；污染物对应环境价值如表2所示.储能电池SOC初始值为0.4，最大值为0.9，最小值为0.2.蓄电池充电效率为1，放电效率为0.96.其中表1为风机、光伏和柴油发电机参数，表2为污染物对应环境价值[17].在此微电网配置下，本节以微电网直接经济成本、需求侧响应成本以及综合碳排放治理成本为目标函数，考虑功率平衡约束、设备约束以及系统规划约束条件对此微电网进行优化调度，并通过峰值消减指数、可再生能源消纳率以及用户舒适度三个需求侧响应指标来量化需求侧响应效益.

表1 风机、光伏和柴油发电机参数

表2 污染物对应环境价值

3.2 仿真结果分析

区域光伏功率、风电功率以及负荷的预测值，如图2所示.系统负荷、新能源总出力以及净负荷对比情况，如图3所示.净负荷表示的是WT、PV满足负荷后的剩余功率.从图2可以看出新能源出力与用电负荷的时序性并不一致.0时到下午4时系统中存在过剩功率，而在4时之后又出现功率不足的现象.为了保证该地区的供电可靠性，同时最大程度的利用本地风光等可再生能源，需要通过增加储能装置或者实施需求侧响应措施.为了研究储能系统和需求侧响应在微电网中削峰填谷能力和可再生能源消纳率的影响，分别设计了4个情景进行对比优化分析：

情景一：系统中不含储能和需求侧响应.

情景二：系统中只含储能装置.

情景二：系统只考虑需求侧响应.

情景四：系统中同时采用储能装置和需求侧响应，两者联合运行.

图2 光伏风电以及负荷的预测值 图3 各种负荷对比情况

3.2.1 情景1调度结果分析

场景一中各微电源出力情况如图4所示；从图4可以看出，下午4时之后尽管柴油发电机以最大功率供负荷，系统中仍存在大量负荷未得到满足.运行成本为7 949.7元，碳排放治理成本为998.5元，峰值功率消减指数为0.524，新能源消纳率为77.6%，由于未进行负荷转移，用户舒适度为1，未满足负荷占比为14.6%.

图4 场景一各微电源出力情况图 图5 场景二各微电源出力情况

3.2.2 场景2调度结果分析

场景二中各微电源出力情况如图5所示；加入蓄电池之后蓄电池充放电功率如图6所示.从图5可以看出在净负荷为负的时刻仍有部分未满足的负荷.从图6可以看出在净负荷为正时，多余的功率对蓄电池充电而在净负荷为负时蓄电池放电.与情景一相比，由于加入蓄电池储能运行成本增加为7 536.4元，新能源消纳率增加为81.2%，未满足负荷占比降低为3.4%，碳排放治理成本为849.5元；由于未进行负荷转移，峰值功率消减指数为0.628，用户舒适度仍为1.

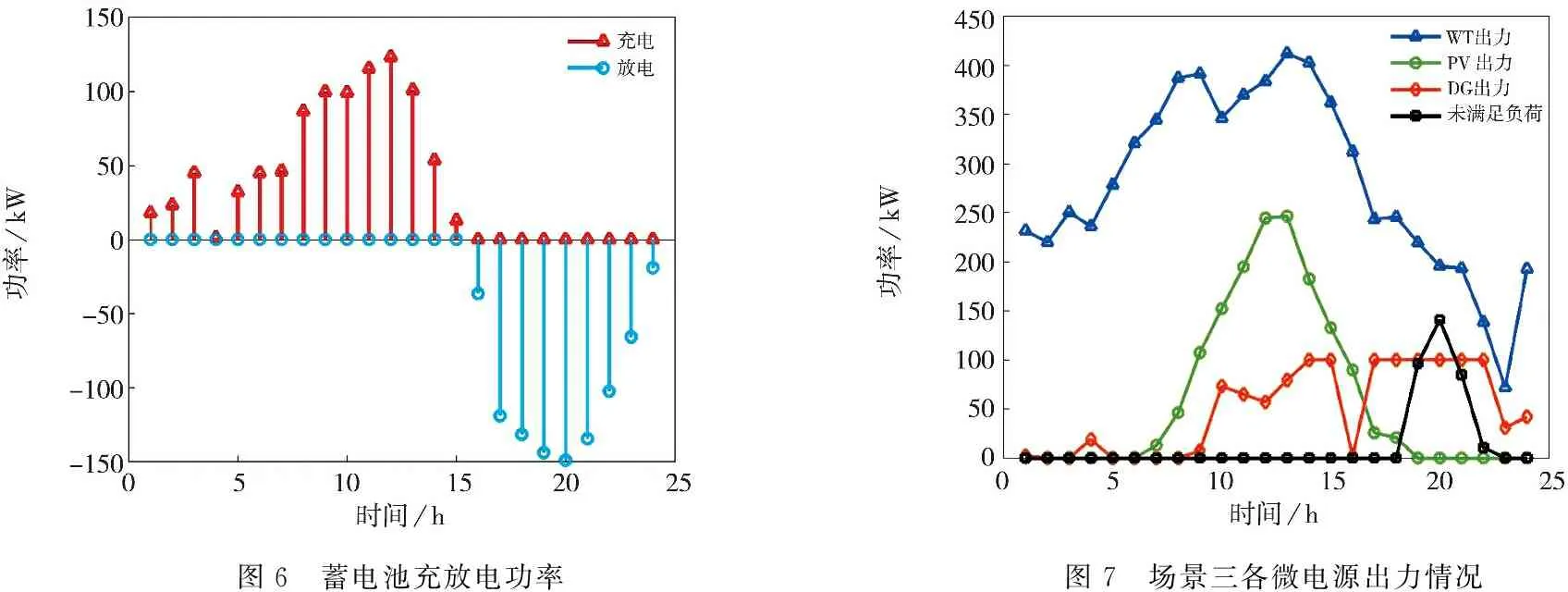
图6 蓄电池充放电功率图7 场景三各微电源出力情况

3.2.3 场景3调度结果分析

场景三中各微电源出力情况如图7所示；需求侧响应前后负荷对比情况如图8所示；负荷转入转出情况如图9所示.从图7可以看出在净负荷为负的时刻仍有部分未满足的负荷.与情景一相比，由于增加了需求侧响应措施，运行成本增加为7 754.9元，碳排放治理成本为734.5元，新能源消纳率增加为84.7%，未满足负荷占比降低为4.1%；由于进行了负荷转移，峰值功率消减指数增加为0.634，用户舒适度降低为0.684.

图8 需求侧响应前后负荷对比情况图9 负荷转入转出情况

3.2.4 场景4调度结果分析

场景四各微电源出力情况如图10所示；加入蓄电池之后蓄电池充放电功率如图11所示；需求侧响应前后负荷对比情况如图12所示；负荷转入转出情况如图13所示.从图10可以看出系统中没有未满足的负荷.从图11可以看出在净负荷为正时，多余的功率对蓄电池充电而在净负荷为负时蓄电池放电.由于同时增加了蓄电池储能和需求侧响应措施，较情景二和情景三，运行成本降低为6 985.6元，新能源消纳率为93%，系统中未满足负荷为0，碳排放治理成本为649.8元；较情景三负荷峰值功率消减指数增加为0.812，较情景三相比，由于负荷转入转出时间段减少，因此用户满意度增加为0.896.

表3 四种模式下的各个参数值

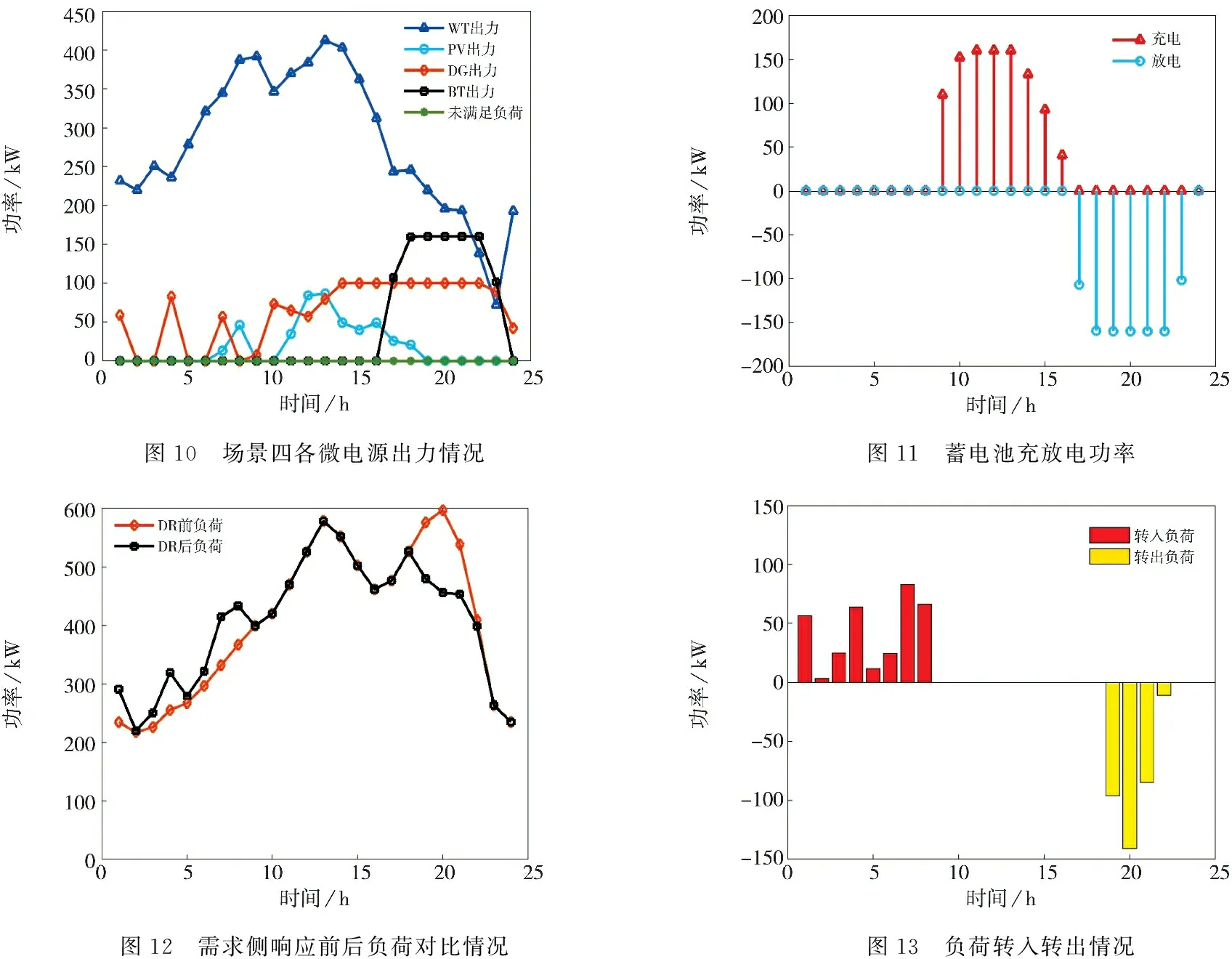
图10 场景四各微电源出力情况图11 蓄电池充放电功率图12 需求侧响应前后负荷对比情况图13 负荷转入转出情况

4 结 论

本文考虑需求侧响应，构建了包含储能系统的微电网“源-储-荷”优化模型，同时设置了两个评价指标来评估需求侧响应效益.为了验证储能和需求侧响应的作用，设立了4种情景，通过对比分析进行验证.结果表明：

(1)储能系统将可再生能源消纳率从77.6%提高到81.2%，同时降低了系统中未满足负荷占比，提高了微电网系统用户用电的可靠性.

(2)需求侧响应的引入也能够在一定程度上降低未满足负荷占比，同时可以改变负荷结构，使负荷曲线在时序上更加贴近新能源发电曲线，从而将可再生能源消纳率从81.2%提高到84.7%.

(3)同时引入储能系统和需求侧响应可以使二者对提高可再生能源消纳率的作用更为明显，即将该数值从84.7%提高到93.7%，比二者单独作用时的效果更佳，同时降低微电网内未满足负荷为0，增加了微电网的运行可靠性.