数学课程思政的探索与实践

陈航

摘 要：思想政治教育在高校立德树人过程中占据着重要地位。微分几何是一门具有重要理论研究价值和应用价值的数学专业课程。本文主要分享了在全方位育人导向下，将思想政治教育元素融入微分几何课程教学过程的探索和实践。

关键词：课程思政;立德树人;微分几何;教学方法

一、引言

高校肩负着培养社会主义事业接班人的重要使命。在专业课程中践行课程思政，是每位大学教师都应该思考的问题。教师应明白，教书育人的目的在于“知识传播、能力培养、价值塑造”。知识传播是教学的应有之义，考验了教师的专业知识水平;而能力培养、价值塑造则属于课程思政的范畴，需要教师在本专业知识的基础上进一步深入思考并发掘。这对教师的综合教学能力提出了更高的要求。

笔者自2016年以来一直为数学系本科学生讲授微分几何课程。该课程内容属于数学中具有悠久历史和丰富内容的一门分支——几何学，除了具有重要的基础理论研究价值，在工程建设、工业设计以及计算机图像处理等方面均有着广泛的应用。在教学实践中，笔者初步探索了将思想政治教育元素引入课堂教学的方法和路径，希望在传授学生理论知识的同时，提升学生分析问题、解决问题的能力，培养学生独立思考、敢于质疑、不畏困难的科研精神，陶冶学生的情操，进而帮助学生树立并完善正确的人生观、世界观和价值观。

二、课程思政的教学内容

要开展好课程思政工作，首先需要发掘课程中的思政元素。下面以微分几何为例，重点阐述一系列课程思政的教学内容。需要强调的是，同一个内容或知识点可以发掘出不同的思政元素，同一个思政元素也可能蕴含于不同的内容或知识点（见表1）。

1.建立马克思主义哲学的世界观和方法论

（1）实践论：从实践中来，到实践中去。几何学（Geometry）是数学中一门具有悠久历史的分支。早在2000多年前，古希腊数学家欧几里得著成了流传至今的数学经典《几何原本》，系统讲述了“数”与“形”。其中，“形”的内容就是如今的欧几里得几何。几何学源于人类在认识世界过程中对测量（如长度、面积、夹角）的需求，其英文词根“geo-” 和“-metry”分别来源于古希腊语中的“大地”和“测量”。人们在生产生活实践中产生了测量的问题和需求，而后进行归纳抽象，将其转化为数学语言，再通过逻辑推理得到各種定理，最后将定理运用到实践中去，在实践中得到验证。

（2）认识论：事物发展的螺旋式。列宁指出：“人的认识不是直线（也就是说，不是沿着直线进行的），而是无限地近似于一串圆圈、近似于螺旋式的曲线。”[1]人类对数学的认识、数学学科的发展也是如此。到目前为止，人类在数学上经历了三次数学危机，每经历一次，认识就会加深一层。在几何学上，经历了从欧几里得几何学到非欧几何学的曲折历程。在对几何学本质的认识上，也经历了从“朴素的形——点、线、面、体及其测量”到“变换下的不变量”的升华。从经典的三维空间中的曲线曲面论到更加抽象的黎曼几何，体现了人类从外蕴到内蕴、从低维到高维的认识过程。

（3）现象和本质的辩证统一。任何现象都是本质的某种表现，任何本质都要通过某些现象表现出来。现象是表面的、具体的、易感知的，如人们能直观感受到半径越大的圆周越平坦、球面如果不允许拉伸等操作是不能展为平面的。本质则是隐藏在事物内部的、相对稳定的、具有一般性的根本属性，往往只能依靠抽象思维来把握，这正是数学尤其是几何学的特点。我们通过引入曲率这一几何不变量，可以定量地反映光滑曲线在某一点处弯曲程度;通过证明“能够建立局部等距的两个曲面其Gauss曲率在对应点处相等”，反证球面和平面不能局部等距，从而解释为什么不能制作出一张“完美”的平面世界地图。

马克思在《资本论》中写道：“如果事物的表现形式和事物的本质会直接合而为一，一切科学就都成为多余的了。”[2]因此，我们需要透过现象去认识本质，这在人们对几何学本身的认识上有着直接的体现。到19世纪后期，除了古老的欧几里得几何，仿射几何、射影几何已得到发展，非欧几何（椭圆几何、双曲几何）也已诞生。德国数学家菲利克斯·克莱因于1872年发表了著名的埃尔朗根纲领，将这些形形色色的几何学统一了起来。该纲领的核心思想是，将不同的变换群和不同的几何学对应起来，各种几何学主要研究的就是几何对象在群作用下的不变量。这让我们加深了对几何学本质的认识。

（4）整体和部分的辩证统一。在讲解曲面的定义时，我们先后给出曲面的局部定义和整体定义，指出可以将局部的曲面片“拼接”为整体曲面，也可以将整体曲面化为部分的曲面片。另一方面，通过对比圆柱面和莫比乌斯带、环面和克莱因瓶等例子可以看出，即使部分（局部）一样，形成的整体也可能不同。一般来说曲面的局部性质不能完全刻画整体性质。

（5）绝对与相对的辩证统一。在讲解曲面的第一、第二基本形式时，我们强调，当曲面参数发生变化时，其作为二阶对称张量，在自然基底下的分量会相应变化，但带上基底之后整体是不变的。分量是相对的，依赖于参数选取;但第一、第二基本形式是绝对的，不随参数选取的变化而变化。

在计算曲面上曲线的曲率时，我们通过将曲线的曲率向量分解为沿曲面的切向和法向部分，分别引出（内蕴的）测地曲率和（外蕴的）法曲率两个概念。曲线的曲率反映了曲线本身的绝对弯曲程度，而测地曲率和法曲率分别反映了曲线相对于曲面的弯曲程度和曲面相对于三维欧氏空间的弯曲程度。严格来说，曲线本身的绝对弯曲程度其实是曲线相对于三维欧氏空间的弯曲程度。

2.锻炼优秀品质，陶冶高尚情操，塑造健全人格

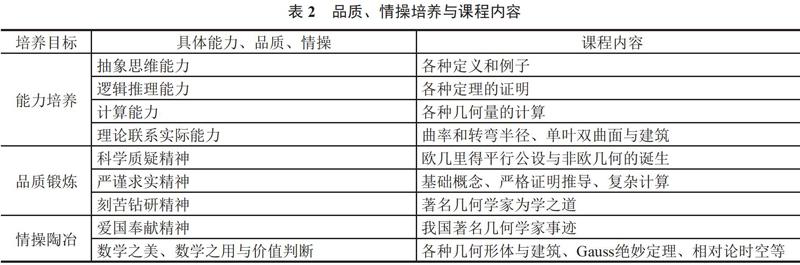
我们希望学生在本门课程中除了学习专业知识外，还能够跳出知识本身，发现具有普适性的、能够全面提升自己的教育元素（见表2）。

（1）能力培养。数学学科的一个重要特点，就是把具体事物抽象为数学语言。在本门课程中，我们可以通过介绍曲线、曲面的具体例子及其严格的数学定义等内容，培养学生提取事物共性的抽象思维能力。

数学研究的另一个重要特点，就是通过严密的推导得到重要结论。我们通过如曲线论基本定理、全脐点曲面分类定理、Gauss绝妙定理、Gauss-Bonnet定理等课程核心定理的证明，训练学生的逻辑推理能力。

几何课程涉及大量计算，有的计算还比较复杂，比如Christoffel符号、Riemann曲率张量的计算。我们通过课上例题和课后习题，训练学生的计算能力。

微分几何同实际生产生活有着紧密的联系。我们适当介绍相关内容，如建筑设计、地理测量等，培养学生理论联系实际的能力。

（2）品质锻炼。中国有句古话：“尽信书不如无书”（《孟子·尽心下》）。在科学研究中，质疑精神是科学发展的推动力。如果没有质疑精神，就会故步自封，不可能取得进步。以几何学为例，如果没有人们对欧几里得第五公设（平行公设）的持续质疑，就不可能由高斯（1777—1855）、黎曼（1826—1866）、罗巴切夫斯基（1792—1856）等人开创的非欧几何学。

这里说的质疑，是建立在科学基础之上的合理质疑，而非毫无科学依据地怀疑一切。在提出质疑之后，我们应当通过科学的研究方法，验证或推翻某个命题。这一切都要经过严格的训练，因此我们需要通过前面提到的基础概念、证明、计算，培养学生严谨求实的作风。

数学专业课的一大特点是抽象，相较其他专业课程更难学、更枯燥。教师除了通过改善讲课语言风格、适当增加互动性等方式引导学生，还应该要求学生克服拈轻怕重的畏难情绪，迎难而上，勇攀高峰。只有经过“山重水复疑无路”的迷茫，才能体会“柳暗花明又一村”的欣喜。教师可以结合课程内容，适当介绍著名数学家特别是华人几何学家陈省身先生、丘成桐先生的为学之道来激励学生。

（3）情操陶冶。除了为学之道，值得学生学习的还有数学大师们致力于中国数学发展、培养本土人才的故土情结和爱国奉献精神，这是陶冶学生情操、培养学生正确价值观的重要一环。

在数学类课程教学中，很多学生会问老师“这个有什么用、那个有什么用”。诚然，数学之用在生产生活各个方面都有体现，关键是要引导学生去发现。另外，学生提出的“有用”，很多时候是从一种略带功利主义色彩的实用性、技术性角度去考虑，这在工科学生中体现得尤为明显。教师需要引导学生思考的是，如果某个数学真的“无用”，是否就不值得花时间学习？

数学源于生活，但很多时候，数学是超前于生活的。我们看待事物，不应该只看短期利益，而要把目光放长远，不能以短期的“无用”判断长远的“有用”，即使这个“有用”可能几代人都见不到。以几何学为例，古希腊几何学家阿波罗尼乌斯（公元前262年—公元前190 年）就已著成《圆锥曲线论》，但1000多年后德国天文学家开普勒（1571—1630）才提出包含“行星绕太阳运动轨道是椭圆”在内的行星运动三定律，揭示了圆锥曲线在天文学上的运用。1854年黎曼为申请哥廷根大学职位而做的开创性演讲“论作为几何学基础的假设”，被视为黎曼几何学的开山之作。尽管黎曼几何纯粹基于数学提出，但几十年后在广义相对论中却得到了极其重要的应用。

即使人们具备了“风物长宜放眼量”的思考方式，很多时候也不具备洞见某种东西长远是否“有用”的能力。那么，就需要在当下从其他方面重新审视“有用”和“无用”。如果仅从工程技术的实用性出发，哲学、文学、艺术、法律等学科都是无用的，但它们都是人类文明的重要组成部分，一旦缺失将会带来非常可怕的后果。俄国唯物主义哲学家、文学评论家车尔尼雪夫斯基（1828—1889）说：“科学书籍让人免于愚昧，而文艺作品则使人摆脱粗鄙;对真正的教育和对人们的幸福来说，二者同样的有益和必要。”英国著名数学家哈代（1877—1947）在《一个数学家的辩白》中写道：“用实践的标准来衡量，我的数学生涯的价值是零;而在数学之外，我的一生无论如何都是平凡的。”[3]数学就像科学中的艺术，即使真的没有“实用”价值，人们也可以学会从纯粹美学角度去欣赏数学。大道至简，好的数学定理有一种简洁之美，能用最简单的语言描述最深刻的道理，如高斯絕妙定理、Gauss-Bonnet定理，这些简洁而深刻的定理无不体现着人类智慧的结晶。即使从纯粹的美学角度，也是值得人们花时间去学习的。此外，“他山之石，可以攻玉”。理工科学生在保证学业的前提下，应该尽可能涉猎哲学、文学、艺术、法律等人文学科知识，这无论对提升专业学问水平、还是塑造健全人格都具有促进作用。丘成桐先生在多个公开演讲中提到，文学艺术和感情培养在其科研历程中起到了重要作用[4]。

三、课程思政的教学方法

对课程思政来说，发掘出课程的思政元素仅仅是准备工作，更重要的是在教学过程中将其传递给学生。为了更好地将思政元素与专业知识相结合，教师需要进一步优化教学内容、创新教学方法和改革教学模式。笔者认为，将思政元素融入教学过程要自然，要水到渠成地娓娓道来，不要高高在上地强行说教，更不能为了思政而思政，强行将风马牛不相及的内容拉到一起。

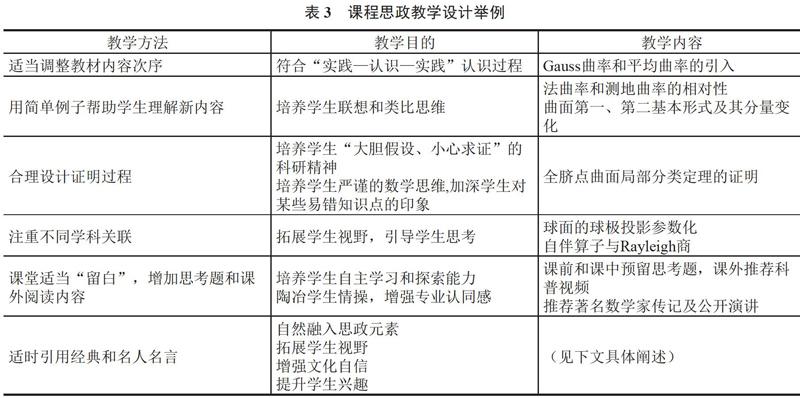
下面笔者分享一些微分几何课程思政的教学设计，并具体阐述各种教学方法（见表3）。需要指出的是，表中的教学方法应根据不同授课内容或知识点灵活运用，并非一成不变。对同一知识点，还可以综合运用不同的教学方法讲授，融入不同思政元素。

1.适当调整教材内容次序

现行数学教材内容大多按照“定义—例子，定理—证明”顺序编排，是一种演绎的方法，与科学探索中“从实践到认识、从具体到抽象”的归纳方法相反。我们在具体授课过程中不能照本宣科，而是要尽量还原科学探索的本来顺序，从具体问题和例子入手，引导学生探索其共性特征和本质，从而归纳提取出抽象定义与重要结论。例如，在引入Gauss曲率和平均曲率时，我们通过探索Weingarten变换在不同参数下的矩阵表示是相似矩阵，得到矩阵的特征值是不同参数下的不变量，进而自然地引出Gauss曲率和平均曲率这两个几何量，同时也印证了几何学就是要寻找变化中的不变量这一核心主题。

2.用简单例子帮助学生理解内容

为了达到更好的教学效果，教师可以也应该通过简单的、直观的、较为熟悉的概念，帮助学生理解一些专业的、抽象的、初次接触的概念。例如，为帮助学生理解曲面上曲线的弯曲程度由曲线相对于曲面的弯曲程度（测地曲率）和曲面相对于三维欧氏空间的弯曲程度（法曲率）叠加而成，我们举了“人在汽车上转动90度和车头相对地面转90度，从而人相对地面转180度”的例子作为类比。

3.合理设计证明过程

科学探索的一个基本步骤是“大胆猜测、小心求证”。求证好比是一个探路并到达终点的过程，我们需要先有一个大致方向（思路），然后再设定几个途经点（分解步骤），通过寻找能够到达下一个途经点的方法（补充完善细节），完成最终的证明。另外，在很多情况下，求证过程不可能一蹴而就，需要经历一次或多次试错，找到“此路不通”的根源，进而打通道路或者另寻他路。以讲授全脐点曲面的（局部）分类定理为例，我们先有平面和球面作为例子，然后“大胆猜测”全脐点曲面仅有这两种，进而“小心求证”。但在证明过程中，我们没有按照正常的证明顺序，而是跳过了学生最容易忽略的地方，先给出一个有“漏洞”的证明，然后引导学生发现并补全漏洞，从而完成整个定理的证明。这种故意留错、让学生寻找的教学设计，有助于加深学生对某些易错知识点的印象，培养学生严密的逻辑思维能力。

4.注重不同学科关联

我们在讲授过程中除了反复提到所用的微积分、线性代数知识作为研究几何的工具外，还注重与数学其他分支、其他学科之间乃至实际生产生活的联系。一个典型例子是，球面的球极投影参数化可以和拓扑学中的单点紧致化定理、复分析中的扩充复平面联系起来，同时指出其在制作地球南北极附近的地图时非常有用。

5.课堂适当“留白”，增加思考题和课外阅读内容

我们在讲授“刚体运动”这部分内容前，先让学生提前思考三维空间旋转的自由度和理论力学欧拉角之间的关系;在讲授“主曲率是法曲率的极值”时，布置线性代数练习题，让学生回顾Rayleigh定理并了解一般的自伴算子特征值的min-max原理;在讲解球极投影参数化时，推荐科普视频《数学漫步——维度》，让学生进一步了解球极投影的性质，以及3Blue1Brown的科普视频，培养学生自学和探索的能力。我们通过推荐著名数学家特别是几何学家的传记以及公开演讲，如陈省身先生的生平事迹[5]、丘成桐先生关于“为学与做人”[6]、“数学与人文”[7]的演讲，陶冶学生情操，增强专业认同感。

6.适时引用经典和名人名言

在教学过程中引用经典和名人名言，可以使课程更自然地融入思政元素，并在拓展学生视野、提升学生兴趣的同时，让学生接受经典文化的熏陶，增强文化自信。

我们一直向学生强调动手演算在数学学习中的重要性，并引用《荀子·儒效篇》中的“不闻不若闻之，闻之不若见之，见之不若知之，知之不若行之”加以佐证。我们还引用《论语·雍也》中的“知之者不如好之者，好之者不如乐之者”，让学生在学习中充分发挥其主观能动性。

教师的一言一行都在影响着学生。《世说新语·德行》记载：“谢公夫人教儿，问太傅：‘那得初不见君教儿？（谢安）答曰：‘我常自教儿。”这充分说明了言传身教的重要性。我们在教学过程中所引用的图片、动画及演示程序等，哪怕是可以公开自由引用的，都会尽量指明出处，潜移默化地向学生传递版权意识与学术道德规范。

参考文献：

[1] 列宁全集：第55卷（第2版）[M].中共中央马克思恩格斯列宁斯大林著作编译局，编译.北京：人民出版社，1990：311.

[2] 马克思恩格斯全集：第25卷[M].中共中央马克思恩格斯列宁斯大林著作编译局，编译.北京：人民出版社，1974：923.

[3] Hardy G H. A mathematicians apology[M].长沙：湖南科学技术出版社，2007：128.

[4] 丘成桐.研学之乐——“数学与人文”系列演讲之一[N].光明日報，2011-01-10（5）.

[5] 张奠宙，王善平.陈省身传[M].天津：南开大学出版社，2004：314-349.

[6] 丘成桐.为学与做人[N].光明日报，2011-12-12（5）.

[7] 丘成桐.数理与人文[EB/OL].[2015-01-09].http：//www.intlpress.net/mh/essay.php？id=357.

[基金项目：中央高校基本科研业务费专项资金“子流形的指标与特征值相关问题 ”（310201911cx013），陕西省自然科学基础研究计划“子流形上椭圆算子的特征值及指标估计”（2020JQ-101）]

[责任编辑：夏鲁惠]