基于多重共线性的气象观测站优化模型

梁素梅

摘要：气象观测站优化问题已成为实际生活中的热点问题，文章根据已有的降水量数据对该市气象观测站之间的相互关系和拟合程度进行了分析;借助EXCEL，EVIEWS3.1，MATLAB等软件进行数据的预处理，对气象观测站问题进行更加深入讨论和相关的分析研究，使得站点的选择问题得到了很好解决。

Abstract： The optimization of meteorological observation stations has become a hot issue in real life. Based on the existing precipitation data， this paper analyzes the relationship and fitting degree between the meteorological observation stations in the city; With the help of EXCEL， EVIEWS3.1， MATLAB and other software for data preprocessing， it conducts more in-depth discussion and related analysis and research on the problems of meteorological observation stations， so that the problem of site selection is well resolved.

关键词：气象观测站;多重共线性;多元统计;回归分析;降水量

Key words： meteorological observation station;multicollinearity;multivariate statistics;regression analysis;precipitation

中图分类号：O212.1                                     文獻标识码：A                                  文章编号：1006-4311（2020）32-0157-04

0  引言

某市有10个县，每个县有一个气象观测站，每个气象观测站测得的年降水量即为该县的年降水量。30年来各观测站测得的年降水量[1]中的B题。为了节省开支，想要适当减少气象观测站，那么减少哪些观测站既可以节省开支，又可以使得该市年降水量的信息量损失较小即信息量足够大？我们究竟应按什么标准来减少观测站呢？这个标准是主观还是客观的呢？如果是客观的，那么减少观测站时应考虑哪些影响因素呢？有没有可能根据这些影响因素来构建一个气象观测站标准的量化模型或定性模型呢？如果可能具体操作又如何呢？如①有人认为第7个观测站和第8个观测站观测到的数据之间有相关关系，第7个观测站可以减少，第7个观测站的年降水量信息可以从第8个观测站观测到的数据中获取。②还有哪些观测站可以减少，减少的观测站的年降水量信息如何获取。③如果以10个县年降水量的平均值为该市年平均降水量。在减少观测站以前，每个县年降水量都是观测数据。在减少观测站以后，被减少的观测站的年降水量只能从其它观测站观测到的数据中获取。减少观测站以前和减少观测站以后是用两种不同测量计算方法得到该市年平均降水量。两种不同测量计算方法得到的该结果会有误差，试预测误差的绝对值小于10mm的概率是多少？误差的绝对值大于20mm的概率是多少？

1  模型假设

①该市的地理特性具有一定的均匀性，即地理因素对气象的影响可忽略不计;

②不考虑该区以外的其它因素对本地区的气象的影响;

③各县建气象观测站的花费是相同的，不随地理的不同而改变;

④信息量足够大是指可预测性在95%以上;

⑤假设预测误差的绝对值服从正态分布，当m值比较大时服从中心极限定理。

2  符号说明

3  减少气象观测站的模型

通过软件EViews3.1分析降水量数据得到各观测站之间的相关系数如表1所示。

从表1中我们可以看出x7和x8的相关系数为0.952268，具有高度相关性，其中x2和x3，x6和x7，x6和x8之间都存在较强的相关性。这反映出它们之间可能存在多重共线性[2-3]。

下面通过软件EViews3.1用VIFi法来诊断多重共线性问题。通过软件EViews3.1算出各变量xi的VIFi值如表2。

从表2中可以看出，VIF8=19.7776，这个数值是很大的，当变量间出现共线性时，可以设法将其消除，用其他变量来表示它，通常选择VIFi值最大的变量进行剔除，所以我们首先可以将x8即第8个观测站减去。它们之间的相关系数为0.952268，具有高度相关性，认为第8个观测站的年降水量信息可以从第7个观测站观测到的数据中获取。但是x2，x3，x6，x7的VIFi值同样也比较大，尤其是x7的VIF7值仅次于VIF8，所以x2，x3，x6，x7中还有可能减少。

当第i个特征值λ≈0时，表示与其对应的主分量对总体的贡献很小，若λi所对应的特征向量vi中第k个分量所占的权重最大，则说明在贡献很小的主成份中起主要作用的是第k个观测站，因此可把第k个观测站剔除掉，剔除它所损失的信息量就是这个主成份的贡献率。对剩下的p-1个观测站的n年观测数据再按上述方法进行计算，看是否需要再剔除另一个观测站;依此进行有限次计算，直到没有特征值近似为0时为止。

在上述过程中剔除了3个测站即x3，x6，x8。因为其剩下的7个观测站就基本上保留了原来气象测站的信息，这样就达到了节省开支，优化测站的目的。

由表2可见λ1=0.0321，λ2=0.0571，λ3=0.0933都是约等于0，第一次计算结果与它们相对应的特征向量v1，v2，v3中，只有v1中的第8个分量的绝对值最大，这时在不损失信息量的情况下删除站x8。由于各测站之间存在相关关系，所以每次只可删除一个测站，再将余下的9个测站30年来的数据按上述方法计算剔除测站x3。第三次将余下的8个测站到按上述方法计算剔除测站x6此计算结束。

综上所述第7个观测站可以减少，第7个观测站的年降水量信息可以从第8个观测站观测到的数据中获取。

4  优化气象观测站模型与回归模型

4.1 模型的分析

要减少观察站，肯定会对降水量信息量有一定的影响，但要求降水信息量损失较小。因此，此处不妨将预测的可靠性设置为95%。首先对表中数据进行分析，可以得出各数据之间的线性相关性[4]，根据95%的可信度，查“检验相关系数ρ=0的临界（rα）表”，可得：

用EVIEWS3.1[7]求的各個相关系数β0，β1，并建立相关的一元线性函数和二元线性函数，再通过F检验线性系数的正确性。过后对模型的建立求解，最后检验模型。并通过误差分析判断出所测数据的置信区间。

4.2 模型的建立

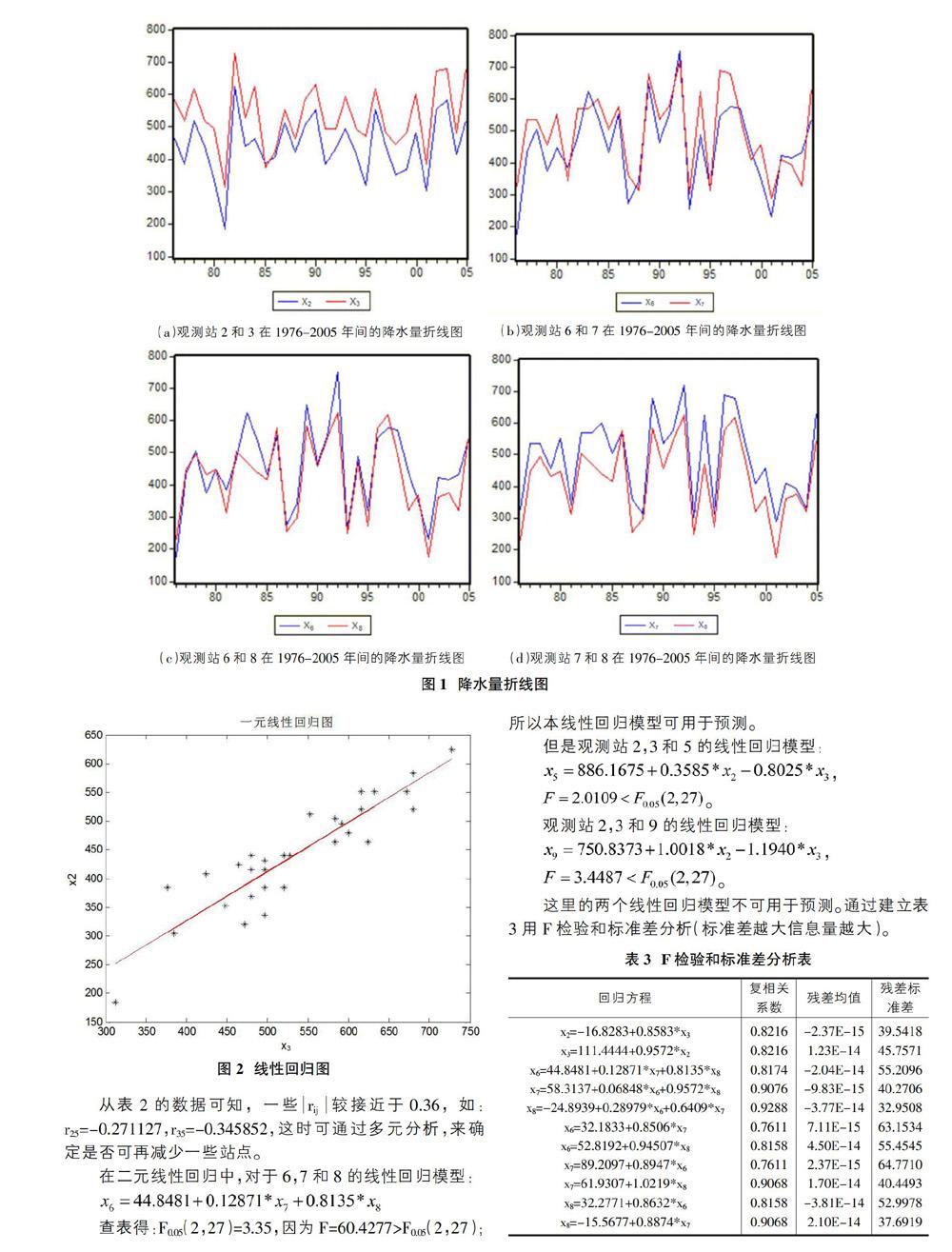
4.2.1 将表中的数据进行折线图的绘图，如图1。

根据图1可知，各观测站之间存在着一定的线性关系，再通过求各观测站之间的线性相关系数，判断是否可以进行各个观测站的线性拟合;又由表2可知：根据95%的可信度，查“检验相关系数ρ=0的临界（rα）表”，可得r0.05（30-2）≈0.36，从表1可查得，rij>0.36的观测站组合：

说明了这四个组合的线性相关性是显著的。

4.2.2 建立一元线性回归模型

对于观测站2和3的线性回归模型为

4.2.3 建立了多元线性回归模型

因为在一元线性回归中，只考虑两者间的相关性，而没有考虑用多个观测站来预测一个站点的情况，因而我们须再进行多元线性回归分析。

从表2的数据可知，一些rij较接近于0.36，如：r25=-0.271127，r35=-0.345852，这时可通过多元分析，来确定是否可再减少一些站点。

在二元线性回归中，对于6，7和8的线性回归模型：

③通过优化模型可以解决第三个问题。

方案1）当建立7个站时候，由于我们选择了x1，x2，x4，x5，x8，x9，x10则预测误差绝对值的均值可用模型2得到误差绝对均值=19.9，方差=227.6，又预测误差的绝对值满足正态分布当θ=10时候根据公式可得：p=2.5，即预测误差的绝对值小于10mm的概率为0.25。

当误差的绝对值大于20mm的概率同理可得p=0.5。

由于m值为30较大，故可以用中心极限定理来求：可知预测误差的绝对值小于10mm的概率p=0.3667。误差的绝对值大于20mm的概率p=0.5。

方案2）当建立8个站时候，由于我们选择了x1，x2，x4，x5，x7，x8，x9，x10则预测误差绝对值的均值可用模型2得到误差绝对均值=10.8，方差=58.1，又预测误差的绝对值满足正态分布当θ=10时候根据公式可得p=0.4602，即预测误差的绝对值小于10mm的概率为0.4602。当误差的绝对值大于20mm的概率同理可得p=0.1736。

由于m值为30较大，故可以用中心极限定理来求：可知预测误差的绝对值小于10mm的概率p=0.53。

误差的绝对值大于20mm的概率p=0.1。

④对②中的两种方案进行讨论

对②中1）虽然建立观测站的开支减少了，但是使得该市的年降水量损失比较大，而对于4中的2）虽然观测站的开支相对1）多了点，但是使得该市的年降水量的信息损失减小了。从上述的讨论，可以看出在开支和信息损失两个角度，如果开支大，得到的信息准确，那么宁愿要选择信息准确的方案。因此，对上述的讨论，采取方案2）是最优的，即在即在市内x1，x2，x4，x5，x7，x8，x9，x10建立气象观测站。

5  结论

依据以上的两种模型，可以对某市的气象站进行一个比较好的规划。气象站的建立固然重要，但是有些不应该建立的站点，应该从费用和实用性双方面来考虑。信息的准确性对于一个市的经济有重要的影响，同时建立的站点并不是越多就越好，对于有些没有必要的站点，可以通过采用就近的方案近似的估计它当年的降水量。通过合理规划既可以节省开支又比较准确地获得了降水量的信息。

参考文献：

[1]http：//www.doc88.com/p-304514289238.html.

[2]周品，赵新芬.数理统计分析[M].北京：国防工业出版社，1989.

[3]于秀，任秀松.多元统计分析[M].北京：中国统计出版社，1999.

[4]袁卫，等.统计学[M].北京：高等教育出版社，2000.

[5]刘来福，曾文艺.数学模型与数学建模[M].北京：北京师范大学出版社，2002.

[6]求是科技，MATLAB7.0从入门到精通[M].北京：人民邮电出版社，2001.

[7]易丹辉.数据分析与EVIEWS应用[M].北京：中国人民出版社，2008.

[8]袁曾任.人工神经元网络及其应用[M].北京：清华大学出版社，1999.