育肥猪舍中的猪叫声端点检测算法
2020-12-27熊梓奥苍岩
熊梓奥,苍岩
哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001
2019 年,由于非洲猪瘟的影响,我国生猪市场遭受冲击,各地养猪场大量生猪病死。在养殖户经济损失巨大的同时,也造成了猪肉价格飙升的情况[1]。猪在患上非洲猪瘟后,最显著的病状就是咳嗽[2]。为预防相关呼吸道传染疾病,提高人工诊断效率,可通过监测猪舍中猪的咳嗽情况,报告给饲养员进行预警。猪咳嗽声监测系统是一个端对端系统,需要对猪舍的声音长时间采集,再来识别其中的猪咳嗽声。由于长时间采集的声音数据量大,包含没有猪叫声的部分,所以在对猪咳嗽声识别之前,需要对采集得到的音频数据进行端点检测。在冗长的音频中确定猪叫声的起点与终点,提取出猪叫声,从而提高系统的检测效率。同时,端点检测算法的检测效果也会直接影响监测系统后续咳嗽声识别的准确率。因此,一个有效且鲁棒的端点检测算法是整个猪咳嗽声监测系统的关键之一。
现阶段端点检测算法大致可分为2 类:第一类是基于阈值比较的方法。这类方法提取样本每帧的特征参数,将其与人为设定的阈值进行比较,然后判定得到语音帧,其最为经典的是基于短时能量和短时过零率的双阈值端点检测算法[3]。它使用短时能量与短时过零率作为特征参数,具有计算量小,检测速度快的特点,但在低信噪比条件下算法的性能急剧下降。由于语音的特征参数易受背景噪声影响,有些研究者便尝试找到更抗噪的特征,文献[4]将子带能量与子带谱熵相结合,提出一种新型语音特征参数——子带能量熵比。除此之外,文献[5]引入了特征组合的方法,以改善单一特征易受噪声影响的问题。第二类是基于模型匹配的方法。这类方法通过样本构建语音模型,再与测试样本进行匹配。在低信噪比情况下,第二类方法比第一类方法的检测结果更准确,但是它需要大量数据进行训练,而且算法相对复杂,计算量大。早期有研究者使用隐马尔可夫模型(hidden Markov model, HMM)算法[6]、支持向量机算法(SVM)[7]以及单一的神经网络作为端点检测的模型。文献[8]对单一神经网络的检测效果做了比较。随着深度学习研究的快速发展,对于端点检测算法的探究从单一神经网络,转向多算法融合。文献[9]将深度神经网络(deep neural networks,DNN)与维特比算法结合,进一步提高检测的准确率。文献[10]提出了一种增强统计噪声抑制算法,并将其作为一个模块,应用于在卷积神经网络前。除此之外,文献[11]搭建了复杂的神经网络模型,将卷积神经网络(convolutional neural networks, CNN)与循环神经网络(recurrent neural network, RNN)结合,进行特征学习。模型输入语音样本原始波形,实现了端到端的端点检测系统。
综上,本文以生猪养殖场育肥舍的应用场景为背景,提出一种基于长短时记忆(LSTM)网络单元的端点检测算法。算法首先通过分析猪舍中的猪叫声信号,提取其梅尔频率倒谱系数(MFCC)与对数能量特征作为模型的输入,再搭建以LSTM为主体的神经网络对猪叫声信号进行端点检测,探究了算法在猪舍风扇噪声下的鲁棒性。
1 算法总述
本文端点检测方案本质上是对猪叫声音频样本进行逐帧判断,确定每一帧是猪叫声还是非猪叫声,从而得到猪叫声的起点和终点。相比于人类,猪叫声种类较少,主要有正常的哼叫声、打架的嚎叫声、患病的咳嗽声,而育肥猪舍的背景噪声也相对单一,大部分情况为风扇声、水声以及猪撞击猪栏的金属声。因此,可以针对猪舍的特点设计整个检测方案。由图1 所示,猪叫声端点检测方案由预处理、特征提取、模型训练、模型检测4 部分组成。
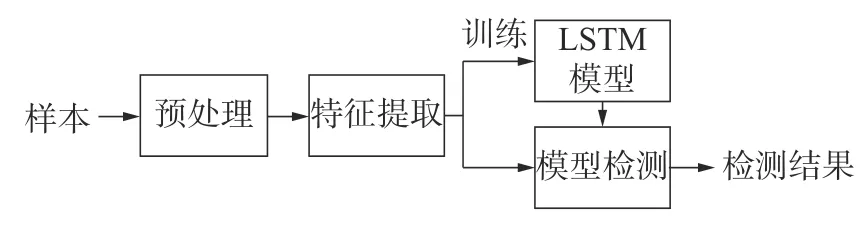
图1 猪叫声端点检测方案
预处理阶段:将样本按比例分为训练集、验证集、测试集,并对每个样本进行预加重、分帧、加窗处理。
特征提取阶段:对预处理后的训练集、验证集中的样本提取可以表征样本的特征参数,即MFCC 和对数能量的组合,减少原始样本的冗余信息,提高训练效率。
模型训练阶段:根据LSTM 可以对样本时间信息学习的特点,搭建以LSTM 为主的神经网络,将提取的特征参数输入网络中训练,并保存训练完成的网络。
模型检测阶段:对测试集样本进行特征提取,输入训练好的神经网络中,输出结果,最后判定得到猪叫声的起点和终点。
2 基于LSTM 的猪叫声端点检测算法
2.1 预加重
语音信号有着低频信噪比大、高频信噪比小的特点。为了改善高频信噪比,需要对猪叫声样本进行预加重处理,提升其高频部分,从而增加高频分辨率。将样本信号通过一个高通滤波器即可实现预加重,高通滤波器的传递函数如下

假设第n时刻的语音采样值为x(n),经过预加重处理后的信号如下
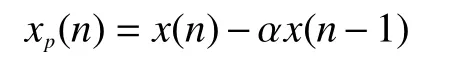
式中α为预加重系数,通常取0.97。
2.2 加窗分帧
语音信号是一种时变信号,但它具有短时平稳特性。在一个较短的时间内,语音信号特性基本保持不变即相对稳定,可以将其视为一个准稳态过程。MFCC 特征参数提取采用短时谱分析,因此对猪叫声信号进行分帧。分帧时相邻帧之间应有部分交叠,以保证帧与帧之间的连贯性。由于分帧后语音帧的两端急剧变化,会导致频域中帧与帧之间过渡时信号发生丢失。将每个语音帧乘以Hamming 窗,使两端平滑过渡到零,从而减小语音帧的截断效应。Hamming 窗函数如下
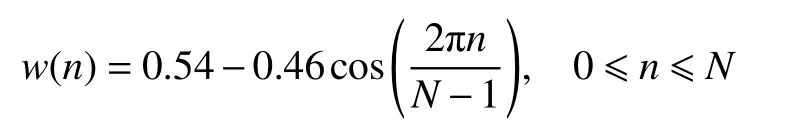
式中N为窗的长度。
2.3 特征提取
MFCC 是 由Davis 和Mermelstein[12]在1980 年提出。研究表明,人耳对低频信号更加敏感。当频率小于1 kHz 时,频率与人耳感知能力呈线性关系;当频率大于1 kHz 时,其呈对数关系。梅尔(Mel)频率就是将实际频率由线性转换为非线性的方法,转换公式如下
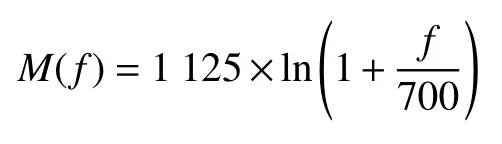
式中f为实际频率。
作为语音信号常见的特征之一,MFCC 模拟了人的听觉特性,适合于语音信号处理的相关工作中。此外,能量也是有效衡量语音和非语音的有效特征。因此,本文选择MFCC 加对数能量作为表征猪叫声样本的特征参数,特征提取步骤如图2 所示。
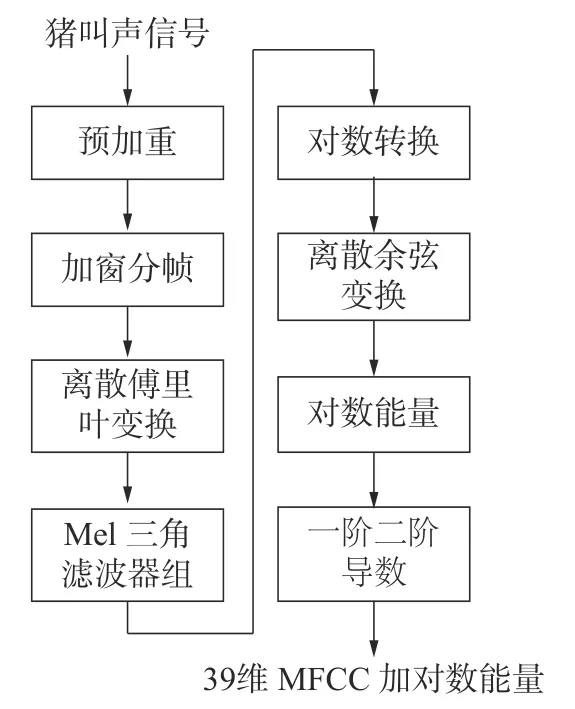
图2 MFCC 加对数能量特征提取步骤
1)将之前预加重、分帧加窗后的猪叫声信号,按帧进行离散傅里叶变换(discrete Fourier transform,DFT)得到样本的频谱

计算功率谱为
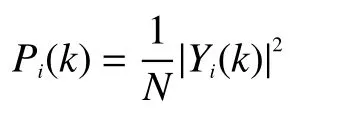
式中:yi(n)为预加重、分帧后的信号;k为傅里叶变换的点数;n表示第i帧中的第n个采样点。
2)将上面的功率谱通过Mel 滤波器组,得到Mel 频谱,公式如下

式中:M为滤波器组中三角滤波器的个数;Hm(k)为Mel 滤波器的频率响应。
3)计算每个滤波器组输出的对数能量,再通过离散余弦变换(discrete Cosine transform,DCT)得到MFCC 系数C,公式如下

式中:M为滤波器组中三角滤波器的个数;I为MFCC 维数。
4)取DCT 后的第2 个到第13 个系数,组成12 维MFCC,再与这一帧的对数能量组合,最终得到这帧语音的13 维特征。
5)通常情况,由于MFCC 与对数能量的组合只能反映猪叫声的静态特征,为了提高模型的检测效果,在13 维特征的基础上计算得到其一阶和二阶导数,组成39 维特征阵。
图3(a)、(b)分别为猪叫声与风扇噪声MFCC加对数能量前13 维特征矩阵的三维特征图,图3(c)、(d)分别为对应的三维特征图的正视图。由于风扇噪声波形幅值随时间变化较小,相对猪叫声更平稳。从图3(c)、(d)中可以看出,每帧的风扇噪声相比于猪叫声,特征值方差更小,特征曲线重合度更高。
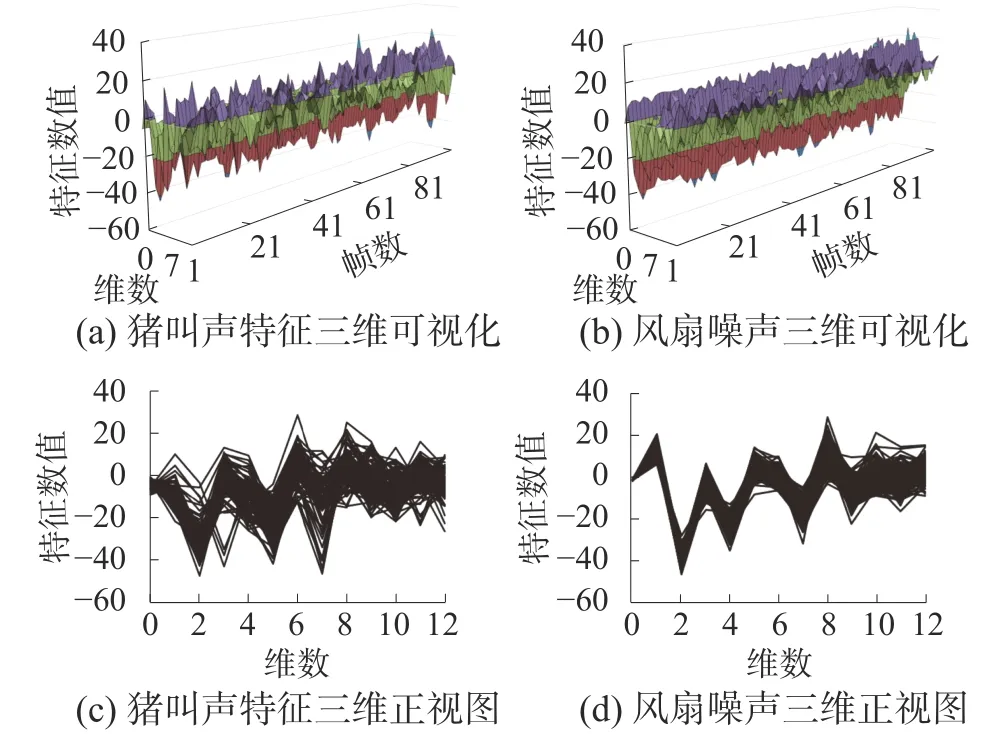
图3 猪叫声与风扇噪声特征对比
2.4 检测模型
长短时记忆(LSTM)网络单元在1997 年由Hochreiter 等[13]提出,它是一种特殊的RNN 结构。它能够对输入的长时依赖关系进行建模,同时在一定程度上解决了RNN 在较长的时间序列上反向传播时带来的梯度消失问题。
在LSTM 的模块中,包含一个输入门,一个输出门和一个遗忘门,通过3 个门的协作来学习权重,达到能够存储长期信息的效果。LSTM 网络单元的结构图如图4 所示。
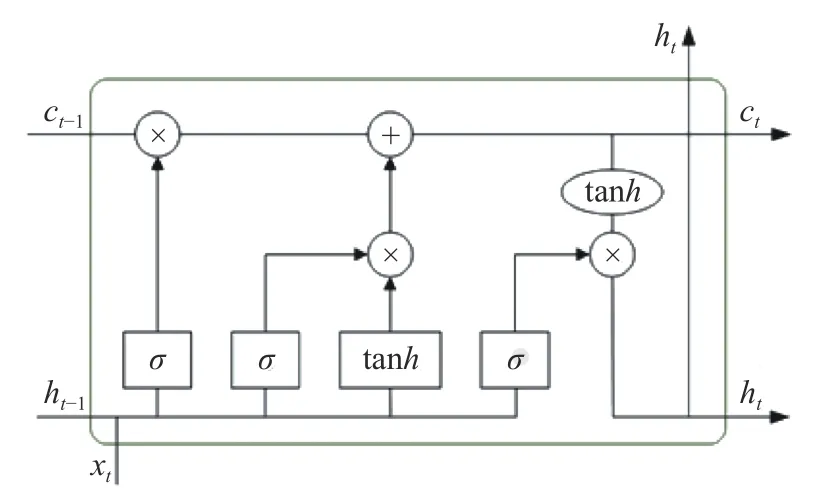
图4 LSTM 网络单元结构
LSTM 内部相关计算公式为
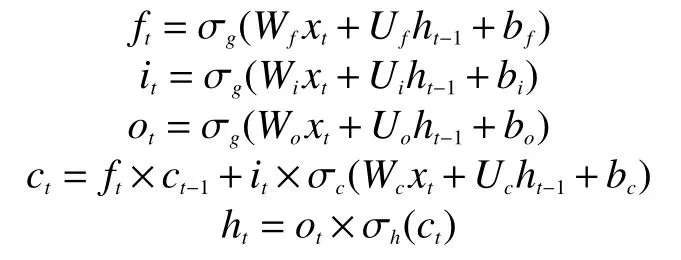
式中:ht是隐藏状态;ct是单元状态;W、U、b为训练中需要学习的参数;ft为遗忘门、it为输入门、ot为输出门,三者的输入均为ht-1和xt,经过激活函数,将值缩放至0 和1 之间。当遗忘门的值取0 时,单元状态ct的值也变为0,相当于遗忘掉上一时刻的状态,只关注此时刻的输入。输入门决定是否接收此时刻的输入,输出门决定是否输出单元状态。
图5 为LSTM 检测模型的网络结构。其中,Linear 表示线性层,ReLU 和Sigmoid 为激活函数。
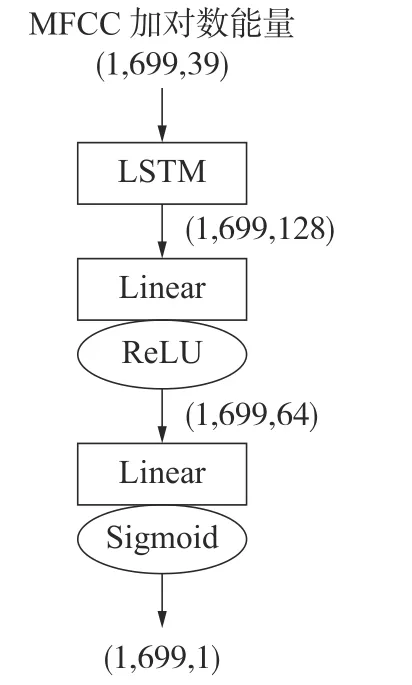
图5 LSTM 检测模型结构
2.5 算法实现步骤
1)对训练集样本进行预加重、分帧和加窗处理。其中,预加重系数α为0.97,帧长为25 ms,帧移为10 ms,窗函数为Hamming 窗。将时长为7 s的音频样本转换成699 个语音帧,得到(1,699)的一维帧矩阵。
2)将人工标记的猪叫声起止时间点,转换为(1,699)的帧标签,语音帧的值为1,非语音帧的值为0。
3)计算训练集样本的39 维MFCC 加对数能量特征。得到尺寸为(39,699)的特征矩阵。
4)将每个特征矩阵转换为(1,699,39)的张量,送入LSTM 模型中训练,模型的输出为(1,699,1)的张量。
5)对模型的输出进行判定,大于阈值判定为语音帧,小于阈值判定为非语音帧,得到检测结果。
3 实验结果及分析
3.1 实验过程
3.1.1 实验数据
本文实验采用的猪叫声数据来自吉林省某生猪养殖场育肥舍,由工作人员使用手机录制。猪舍内有用于控制温度的风扇,当室内温度达到一定程度便自动开启。样本的采集时间是冬季,风扇转动的频率较低。相比于夏季,采集数据没有被风扇噪声干扰的情况更多。数据经过截取处理,去除被风扇声干扰的数据,组成由200 个时长为7 s 的样本构成的数据集。样本的采样频率为16 kHz,采样精度为16 bit。使用Audacity 软件标记样本中猪叫声的起止点,并保存为json 文件,作为语音标签。最后把实验数据按8∶1∶1 的比例分为训练集、验证集、测试集。此外,还额外录制了不含猪叫声的风扇噪声,用于算法的鲁棒性验证。
3.1.2 实验内容
实验1对于端点检测算法,根本目标是要完整检测出猪叫声。模型在输出时由Sigmoid 函数将输出值映射到(0,1),因此需要进行判别,使其值转换为代表语音帧的1,非语音帧的0。如大于阈值0.5 的概率值,则判别为语音帧,反之则判别为非语音帧。这里阈值可以视为一种容忍度,即在保证准确率的前提下,接受一定的误检,而避免漏检,保证检测猪叫声的完整性。为探究判别阈值大小对模型准确率的影响,本实验多次改变阈值的大小,将阈值设置在0.3~0.7,步长为0.1。先使用训练集和验证集训练模型,再使用测试集对训练完成的模型进行评估。
实验2使用基于短时能量和短时过零率的双阈值端点检测算法、基于SVM 的端点检测算法作为对照实验。双阈值算法先提取样本的短时能量和短时过零率,分别设置2 个特征阈值,再沿着时间方向将2 种特征和阈值做比较,得到检测结果。阈值的计算采用自适应方法,对不同的样本选取不同的阈值,以确保算法的检测效果。SVM 算法通过提取样本的多种时频特征构成组合特征,来训练SVM 模型,再使用训练好的模型对测试样本的每一帧进行语音、非语音的二分类,最终得到整个样本的检测结果。SVM 的核函数采用线性核,经过多次实验测试,惩罚因子C选取最优值1,实验结果见图6。

图6 SVM 在不同C 情况下的检测结果
为验证本文算法的鲁棒性,本实验对比3 种算法在加入不同信噪比噪声的数据集下的检测效果。将风扇噪声分别以10、5、0、-5、-10 dB 的信噪比,加入到数据集中,再使用加噪的数据集训练模型。图7 显示了一个样本的原始波形图及其加噪后的波形图。
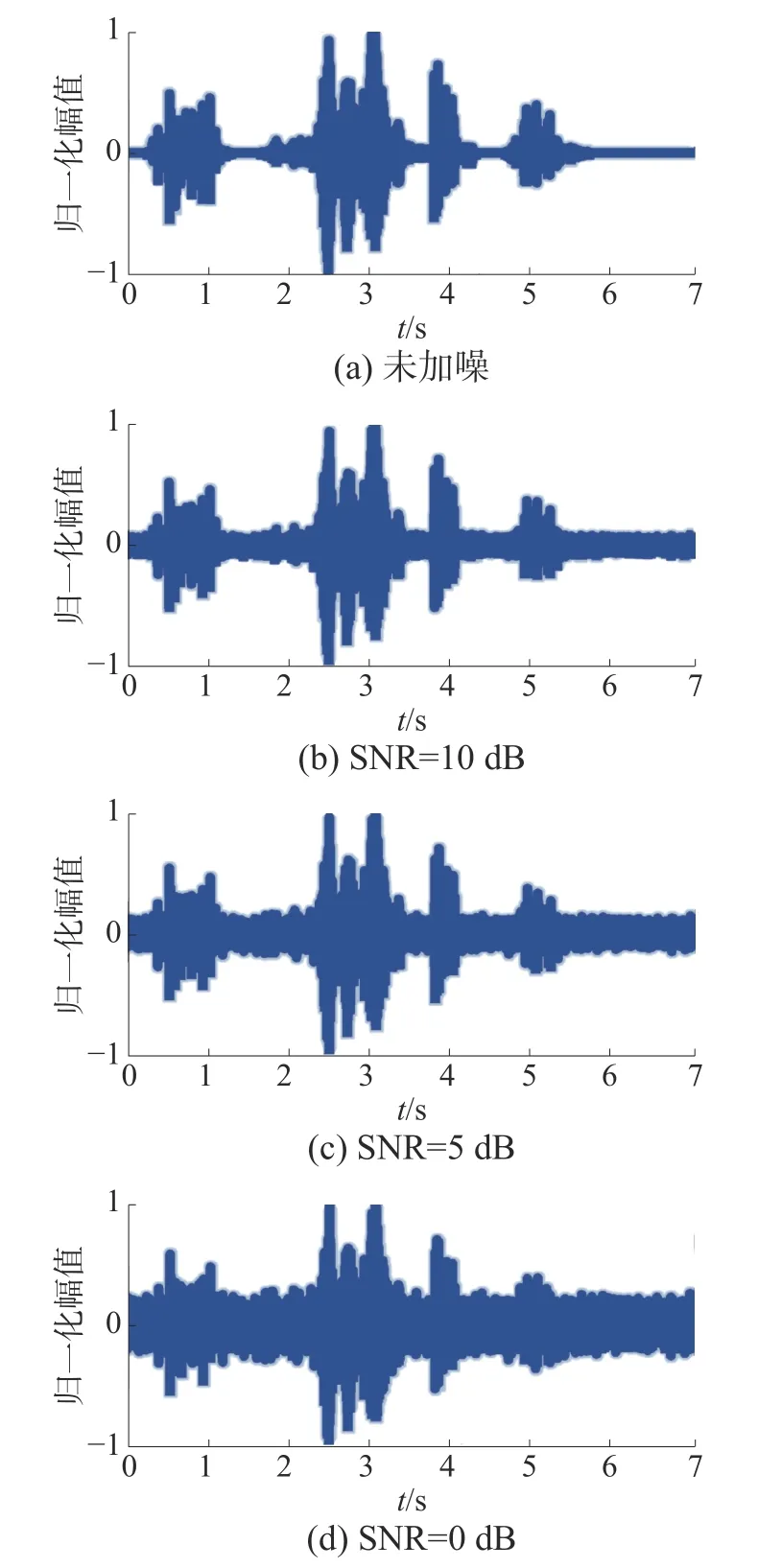

图7 样本的原始波形图及其加噪后的波形
3.2 实验评价指标
为客观评价算法的性能,实验需要比较算法的检测结果与人工标记的起止点,并从以下3 个方面对算法进行评估,

式中:Ns为总帧数;NT为检测正确的帧数;NFR为检测为非语音帧的语音帧数量;NFA为检测为语音帧的非语音帧的数量。
3.3 实验结果分析
3.3.1 实验1
表1 显示了LSTM 模型在不同阈值下,在各个数据集上的表现。
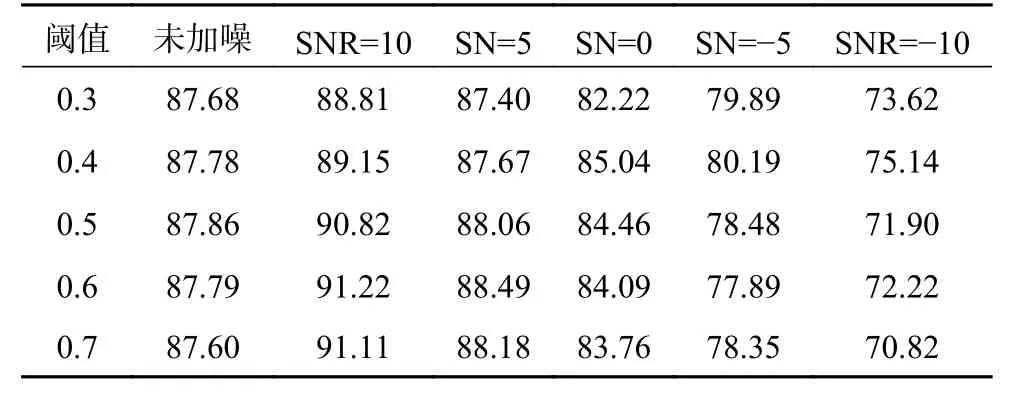
表1 LSTM 模型在不同判定阈值情况下的准确率 %
可以看出,未加噪时,阈值对准确率的影响相对较小;在信噪比较大(10、5 dB)的情况下,最佳阈值等于0.6;信噪比较小(0,-5,-10 dB)时,最佳阈值等于0.4。在测试样本未加噪的情况下,样本中的猪叫声容易被模型检测出来,因此语音帧对应的输出更接近标签值1,准确率没有因为阈值的变化而大幅改变。当测试样本加噪后,在信噪比较大的情况下,猪叫声的幅值远大于风扇噪声的幅值,噪声对检测结果有一定干扰,但干扰相对较小,漏检情况较少。此时,非语音帧对应的输出值会大于0,但又不会大很多,因此较大的阈值会将这类输出值判定为非语音帧,降低了误检率,使得准确率提高。在信噪比较小的情况下,风扇噪声会淹没部分猪叫声,检测结果会受到噪声的严重干扰,语音帧的输出值会更接近非语音帧输出值。此时,较小的阈值会降低检测标准,增加误检率,但保证了更多的猪叫声不被噪声影响而漏检,反而增加了整体的准确率。
3.3.2 实验2
表2 显示了3 种算法在添加了不同信噪比风扇噪声的数据集上的表现,图8 显示了3 种算法在不同信噪比风扇噪声下的准确率。由图8 可以看出,3 种算法的准确率会随着信噪比的减小而降低。
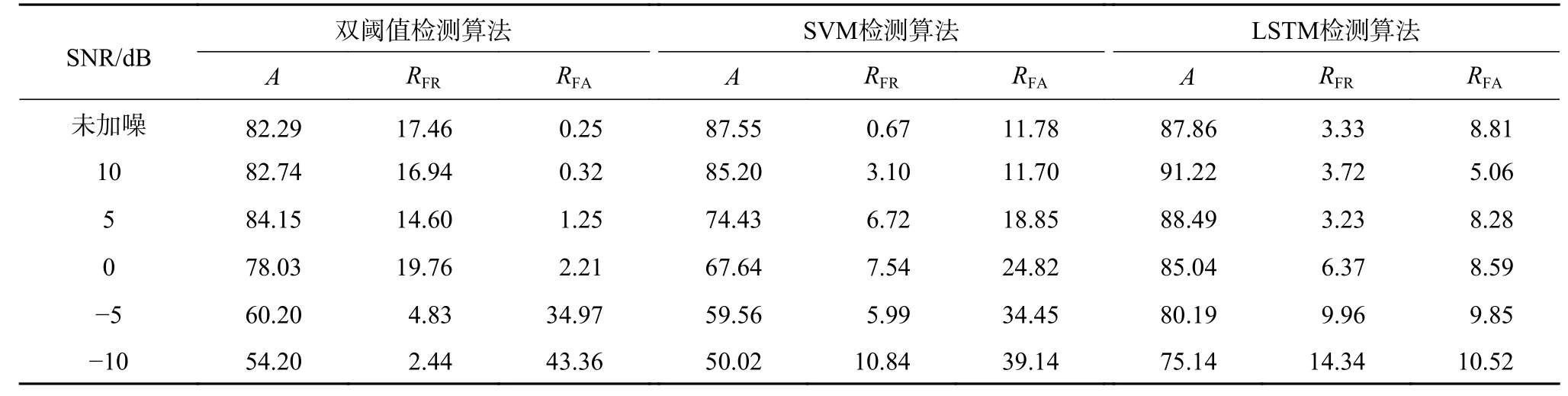
表2 3 种算法在不同信噪比的风扇噪声下的检测结果 %
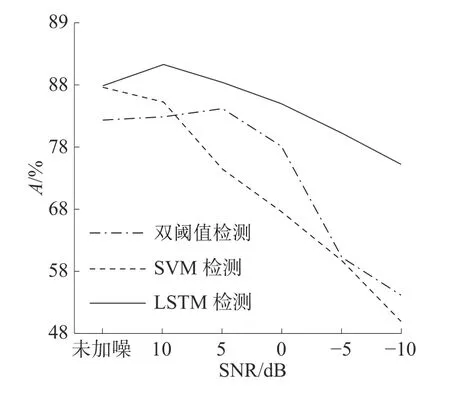
图8 3 种算法在不同信噪比的风扇噪声下的准确率
双阈值检测算法在高信噪比(10、5 dB)的情况下检测效果较理想。但当风扇噪声强度增加,信噪比小于0 时,部分猪叫声被风扇噪声所淹没,猪叫声的短时能量与短时过零率便没有了区分度。这使得算法几乎将整个样本都判定为猪叫声,更少的猪叫声被漏检,更多的风扇噪声被判定为猪叫声,造成了漏检率RFR大幅降低与误检率RFA的激增。图9 为图7(d)样本的双阈值检测结果,从图中可以看出,由于噪声影响,双阈值检测算法将部分噪声误判为猪叫声。

图9 SNR=0 dB 时双阈值检测结果
SVM 算法在信噪比降低的过程中,整体的检测效果变差,A的变化几乎是呈线性降低,RFR和RFA一直增加。这说明了随着噪声强度的增加,猪叫声的时频特征与风扇噪声的时频特征区分度越来越低,SVM 模型很难对猪叫声和风扇噪声进行正确分类。图10 为图7(d)样本的SVM 检测结果,在信噪比为0 dB 的情况下,SVM 模型已无法对样本正确检测。
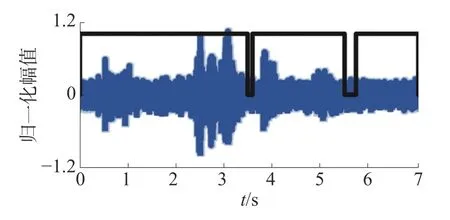
图10 SNR=0 dB 时SVM 检测结果
LSTM 算法相比于其他2 种算法,A、RFR、RFA三者的变化幅度更小,检测结果更加稳定。在信噪比高的情况下,算法检测结果优于其他,即便在较低的信噪比(-5、-10 dB)下也仍有一个理想的检测效果。这说明LSTM 模型通过训练样本学习到了猪叫声的特征,即使在低信噪比时,也能从含噪样本中判定得到猪叫声。因此也证明了LSTM 算法在猪舍的风扇噪声下有着更好的抗噪鲁棒性。图11 为图7(d)样本的LSTM 检测结果,由图可以看出LSTM 模型在较低信噪比时仍然能检测出猪叫声。
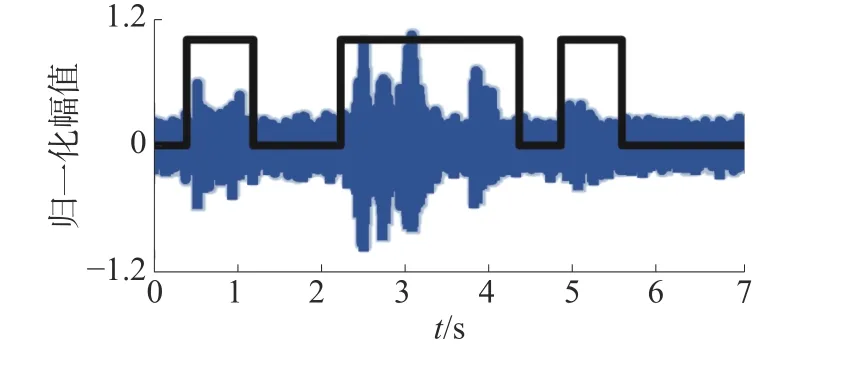
图11 SNR=0 dB 时LSTM 检测结果
4 结论
1) 传统端点检测算法在高信噪比情况下,检测效果良好,但随着噪声强度的增加,算法的准确率也随之大幅降低。本文提出了一种基于LSTM网络单元的端点检测算法,针对风扇噪声的环境,通过大量猪叫声数据训练得到更精准的端点检测模型。
2) 本文进行了2 组实验,实验1 为测试得到LSTM 端点检测模型的最佳判决阈值;实验2 在这个阈值的基础上与双阈值端点检测和SVM 端点检测进行比较。仿真实验结果表明,在猪舍中不同信噪比的风扇噪声下,相比于传统端点检测算法,提出算法的检测效果稳定、鲁棒性好。
本文所提出的LSTM 模型较小,可以通过搭建较复杂的模型,进一步提高检测的效果。未来也可以在数据集中增加其他猪场的猪叫声,以提高模型的泛化能力。
