引入平滑迭代的骨架提取改进算法

袁良友，周 航，韩 丹，许国梁

北京交通大学 电子信息工程学院，北京100044

1 引言

作为计算机视觉领域提取目标特征的处理步骤之一，细化已经广泛应用于指纹识别、字符处理、运动人体分析、测绘信息提取[1-4]等各种应用场景。细化是指在不影响原图像拓扑连接关系的条件下，保持其目标骨架或中轴线，将图像的线条由多像素宽度减少至单位像素宽度，极大消除图像冗余信息的过程，也称骨架化。具有良好效果的细化算法须具有以下特点：迭代收敛、骨架可连通、拓扑结构不变、细节特征可保持、无冗余像素、骨架中心化、实时性好等。细化算法作为一个活跃的研究领域，目前已有一些经典的成果。整体而言细化算法可分为迭代以及非迭代两类，迭代算法分为串行[5]、并行以及串并行混合算法，而非迭代算法基于距离变换或其他原理，处理后的骨架通常缺乏整体连通性。在此背景下，速度快、条件简单的并行算法得到了更广泛应用，代表之一便是Zhang和Suen在文献[6]中提出的ZS细化算法。

ZS算法对拐角、T型交叉点以及直线的结构细化效果较好，能保持其整体连通性以及较快的细化速度。但是大量的实验表明，ZS 算法普遍存在三种处理不当的问题[7]：

问题1 二像素宽度斜线细化出现结构全丢失。

问题2 2×2正方形结构细化后拓扑结构全丢失。

问题3 细化后大量存在二像素宽度的冗余像素。

细化过程中局部信息的丢失将导致可提取特征点的减少，冗余信息会混淆和误导特征点提取的结果，微小结构的丢失则严重影响某些微型结构场景下的细化效果。如何同时处理结构丢失、像素冗余的细化问题显得尤为重要。

因此，产生了各种ZS算法的改进形式，Lu和Wang[8]提出LW 细化算法，去除了B(P0)=2 的删除判定条件，使得二像素斜线结构得到保留，但细化结果出现大量冗余分叉。牟少敏等人[9]通过制作像素周围8邻域的十进制模板，增加了特定模板删除条件，一定程度上解决了冗余像素问题。包建军等人[10]提出EPTA 的鲁棒算法，增加了是否结束第一阶段扫描的判断条件并增加一个二阶段扫描过程，有效改善了局部信息丢失和冗余像素等问题，但其依然存在斜线细化畸变以及冗余消除不完全的问题。赵丹丹等人[11]提出IEPTA 算法，在EPTA 算法的基础上增加了两个对称的映像迭代过程，获得了更加接近中心线的骨架图像，但并没有实现完全对称的细化效果。文献[12]提出了MZS算法，能够完整保留2×2正方形结构，但像素的坐标索引值的奇偶性会对细化结果有直接影响。

好的细化算法应能改善图像线条纹路信息，而不仅仅是消极地进行数据压缩。对于线状图形信息丰富的图像，细化之后除了骨架的大小、形状与原图像保持一致，一般也会存在原图像的表面噪声信息。文献[13]指出，在足够多的迭代次数下，不平滑的表面轮廓会使得细化结果存在第四种问题：

问题4 图像出现较多受噪声影响的轮廓分叉。

文献[14]通过改进删除规则，提出了一种基于轮廓筛检的骨架细化算法，并应用于交通指挥动作骨架提取过程中，但其删除规则的制定依据于人体骨架而不具普遍性。文献[15]提出了一种基于笔划连续性检测的并行细化算法，可以控制笔划交叉或交叉处的大变形，免受表面噪声干扰，但其适用范围局限于字符图像。对于不同类型的二值图像，细化时若能够在删除冗余像素和保留特定结构的前提下减少其表面噪声信息，将大大提高后期特征提取的效果和精度。

为了解决细化过程出现的以上问题，本文在细化过程中加入保留模板和消除模板以处理冗余与结构丢失现象；同时在进行全局的细化迭代前引入一定次数的轮廓平滑迭代过程，有效抑制了实际二值图像的表面噪声带来的分支效应。

引入通用的并行计算平台和编程模型可以加快算法的运算速度[16]。目前，各个并行细化算法的CUDA并行编程模型正在成为研究热点，其算法的并行版本平均可比传统的CPU顺序版本快几十倍以上。

2 细化算法基本原理

2.1 基本定义

规定二值图像的前景点像素为1，背景点像素为0。对某一像素点P0，其8 邻域与24 邻域的像素点集合如图1 所示，P0为扫描点像素，P1～P8为其8 邻域像素，在周围扩展一层像素集合P9～P24得到其24 邻域像素。在细化的迭代过程中，每次迭代的次序记为N，子迭代次序记为S。像素P0的交叉数A(P0)定义为沿其八邻域顺时针环绕一周像素由1变为0的次数，P0的连接数B(P0)定义为其八邻域中像素为1的总数。

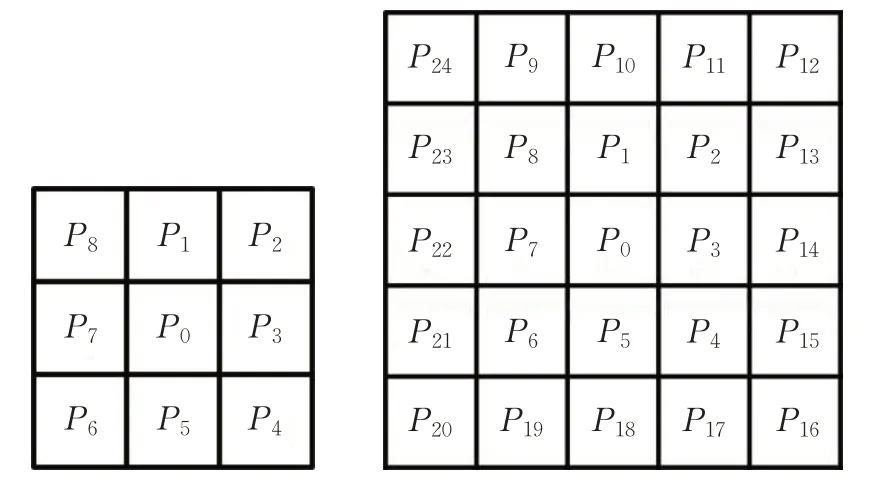
图1 像素8邻域与像素24邻域

2.2 细化约束条件

对于ZS 细化算法，子迭代次数S的奇偶性决定了不同的判断条件。若S为奇数，当每次判断像素点P0满足下列4 个条件，标记为待删除点，并在该子迭代结束时统一删除。

若S为偶数，公式（3）、（4）变为：

当某次迭代中不存在满足删除条件集合的像素，算法结束。

2.3 平滑像素点的判定条件

迭代次数较多的二值图像通常存在不光滑的轮廓，由于目标各处由表面到内部的细化速度是均匀的，最终在各不平滑轮廓的突起处将会形成不同长度的分支。可以推想，当待细化图像拥有平滑程度更高的轮廓，将会得到更少分支的细化结果。

满足公式（1）的目标轮廓像素点可分为平滑像素点与非平滑像素点。如图2，像素点1～4 依次代表了斜方向与水平方向上的平滑像素点，它们满足公式（2）和（7）。

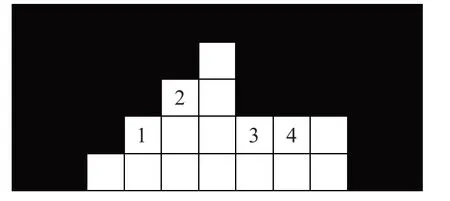
图2 光滑像素点1～4

2.4 保留与删除模板

24邻域可以划分出4个不同方向上的4×4子域，如图3 中的M1～M4 所示，它们适合用来区分不同方向上的特定结构。

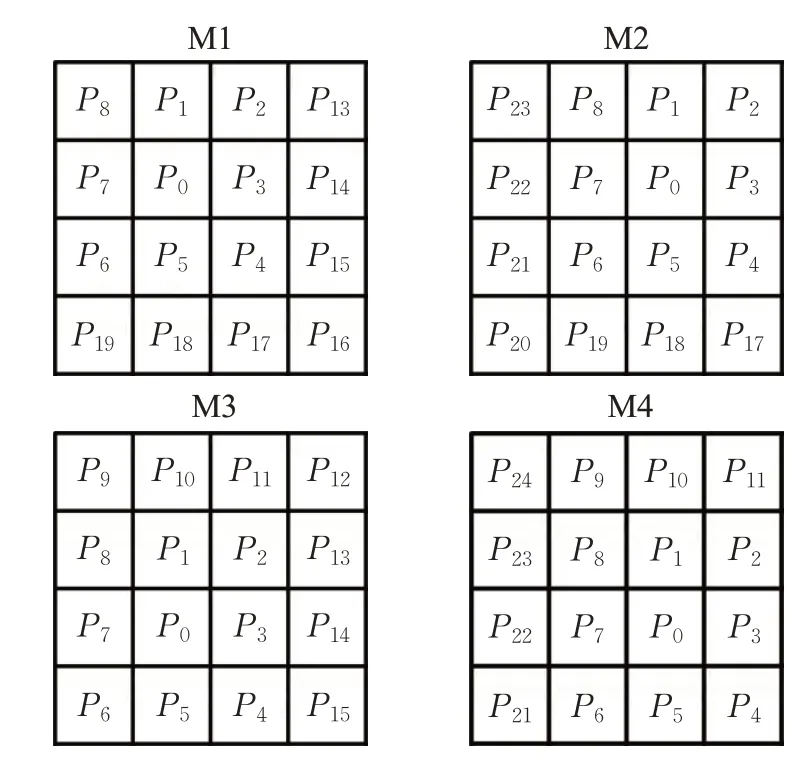
图3 4×4子域

为处理细化过程中的结构丢失与冗余像素问题，分别设计了24 邻域子域下的保留模板以及8 邻域下的删除模板[17]，如图4、图5。模板中的像素点Px可为1也可为0。

3 骨架提取改进算法

3.1 改进算法整体描述

引言中论述的四种问题在不同的细化场景下其处理的优先级是不同的。目标像素总数与迭代次数较少时，问题1～3所代表的拓扑结构丢失与像素冗余问题应当被优先考虑。而当像素总数与整体迭代次数较多时，问题4 中不光滑轮廓引起分支问题的解决对于目标特征提取更加关键。

因此，在进行全局迭代前，本文引入一定次数的平滑迭代过程，用以解决不同场景下的细化问题。在平滑迭代过程中对平滑像素点进行保留，抑制了平滑轮廓出像素点集合的细化速度。同时，为了解决结构和冗余问题，在前期的迭代过程中引入保留模板，而在后续的二阶段扫描过程中引入删除模板。

图4 保留模板

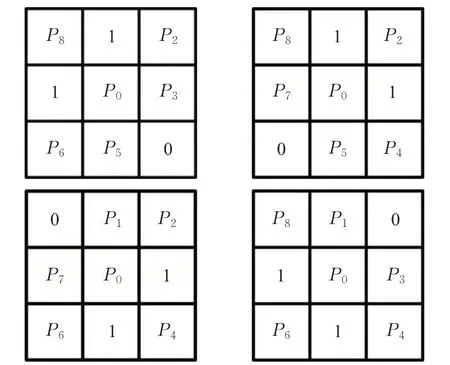
图5 删除模板

3.2 算法细节描述

如图6所示，改进算法将整个细化过程分成三种迭代流程：平滑迭代、全局迭代以及二阶段扫描。针对问题1 和2，在平滑迭代与全局迭代中加入保留模板的判定条件，保留所有既有删除标记又满足保留模板的像素点，从而避免了一些拓扑结构的删除。其中，图4（a）～（h）用来保持二像素宽度斜线，图4（i）用于保持2×2 正方形结构。针对问题3，在二阶段扫描中加入删除模板（图5）的判定条件，挑选出那些不满足删除条件但满足删除模板的像素点进行单独删除，可避免细化结构出现冗余点。不同于全局迭代中添加删除标记的处理过程，直接删除满足删除模板判定条件的像素点，能有效避免拓扑结构的断裂情况出现。对于问题4，引入的K次平滑迭代可以很好地抑制轮廓噪声。在每次迭代过程中，满足公式（1）、（2）的像素点集合代表了所有的目标边缘像素，满足公式（7）的像素点集合代表了轮廓上的所有平滑像素。仅标记所有的不平滑像素点，意味着直接对轮廓噪声进行过滤，使得目标图像在后续的全局迭代过程中能得到更整体化的细化结构。

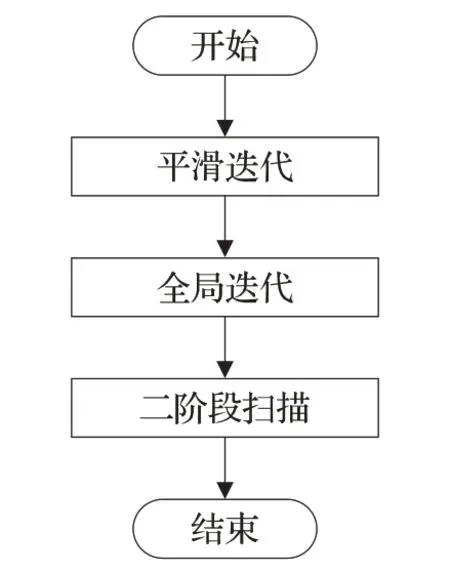
图6 改进算法整体框图

此外，过多的或者不合适的平滑迭代次数会导致提取的骨架出现结构变形。K值的选取应由实际图像的轮廓平滑程度以及前景像素点总数决定。轮廓平滑程度较高，对平滑迭代的要求降低；前景像素点总数较少，对判定条件的敏感度提高，两种情况下K值均应该取较小。

3.3 改进算法流程

修改后的细化算法方案流程如下：

步骤1 根据待细化图像的像素总数和轮廓平滑情况选定平滑迭代次数K，初始化N=0,S=0。

步骤2N＜K时，进行平滑迭代。首先对同时满足公式（1）、（2）的像素点进行删除点标记，再在这些像素集合中除去满足公式（7）以及满足保留模板图4（a）～（i）之一的像素点。每次迭代结束时删除掉有删除标记的像素，N=N+1。

步骤3N≥K时，进行全局迭代。奇数次子迭代对同时满足公式（1）～（4）的像素点进行删除点标记，偶数次子迭代对同时满足公式（1）、（2）、（5）、（6）的像素点进行删除点标记，然后在这些像素集合中除去满足保留模板图4（a）～（i）之一的像素点，每次迭代结束时删除掉所有删除标记的像素，N=N+1,S=S+1。当某次迭代后无删除标记像素时，进入步骤4。

步骤4 进行一次全局迭代的二阶段扫描。扫描过程中直接删除满足删除模板（图5 后两个）的像素点。当迭代后无删除标记像素时，细化结束。

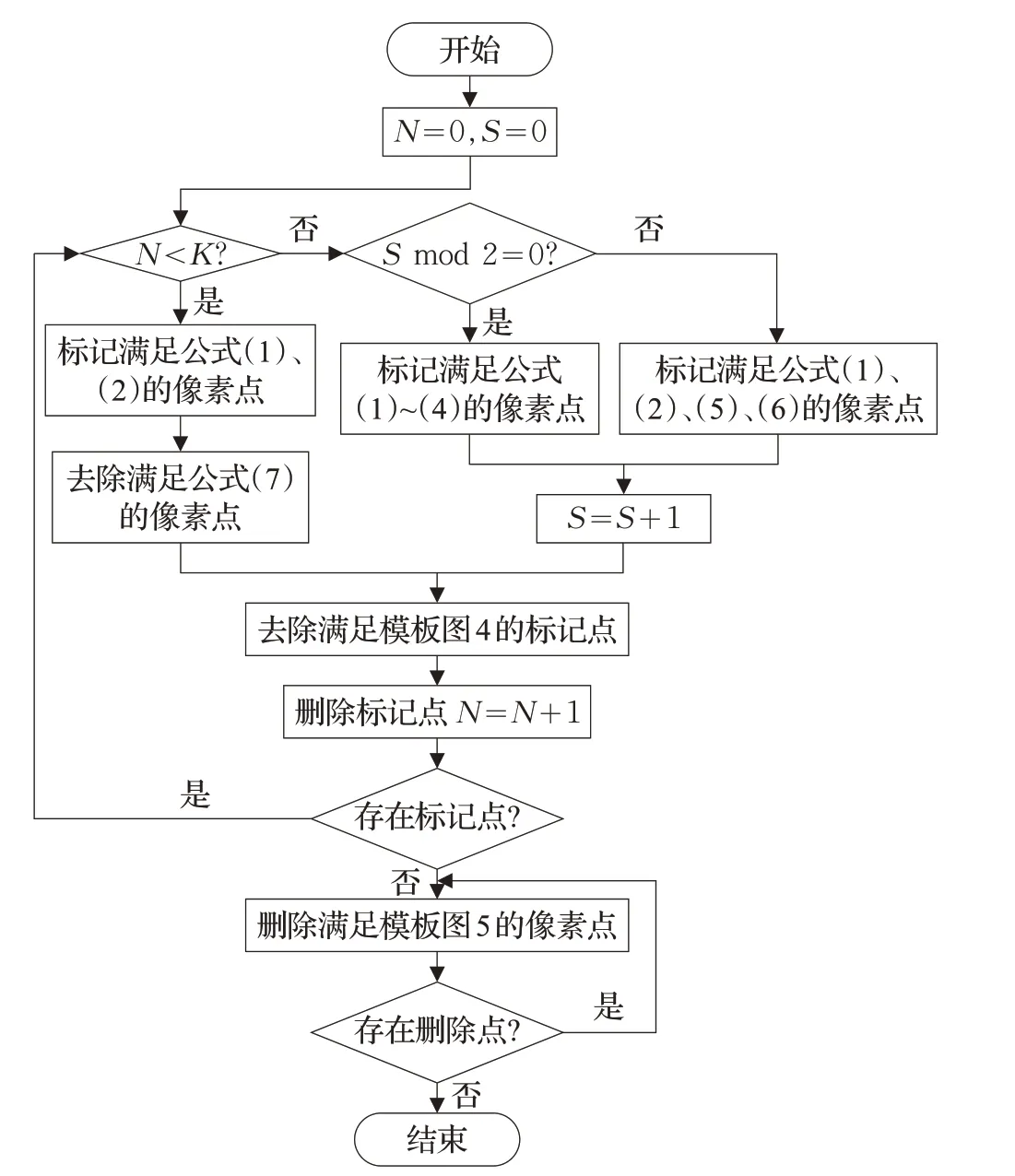
图7 改进算法流程图

图8 二像素宽度斜线细化效果对比

4 改进算法效果及性能

为了检验改进算法对问题1～4的改善效果，本文在Visual Studio 2019 环境下，分别对二像素宽度斜线结构、正方形结构、人体结构以及字母结构进行细化，并将改进算法、经典ZS算法与较新的IEPTA算法、MZS算法细化结果进行比较。考虑到细微结构对平滑迭代的敏感度高，仅在字母结构细化过程中加入平滑迭代。

如图8 所示，相比ZS 算法无法有效保持二像素宽度结构，IEPTA 算法与MZS 算法均解决了二像素斜线细化畸变的问题，但前者细化后的斜线长度有所减少，后者由于判断条件的不对称其结果出现了上下两部分结构的中心偏移。这两种情况在改进算法中均有所改善。

如图9所示，ZS算法和IEPTA算法无法保留左边的2×2 正方形拓扑结构。而MZS 和改进算法均能克服该缺点，同时也能完整保留图右边的两正方形交叉结构。

如图10 所示，ZS 算法处理后人体的右腿部出现较多的冗余像素，而IEPTA、MZS 以及改进算法均实现了对冗余像素的去除。其中，IEPTA 算法由于从4 个方向上进行迭代且加入删除冗余信息的消除模板，处理后的人体骨架较为光滑，但其手部区域也相应地出现了结构丢失。MZS 算法保留的骨架具有较好的连通性，但没有充分删除诸如右脚处的分叉像素点，易受表面噪声的影响。改进算法保持了具有良好连通性的ZS算法细化后的主干结构，同时对噪声点像素也能合理的去除。

图9 正方形细化效果对比

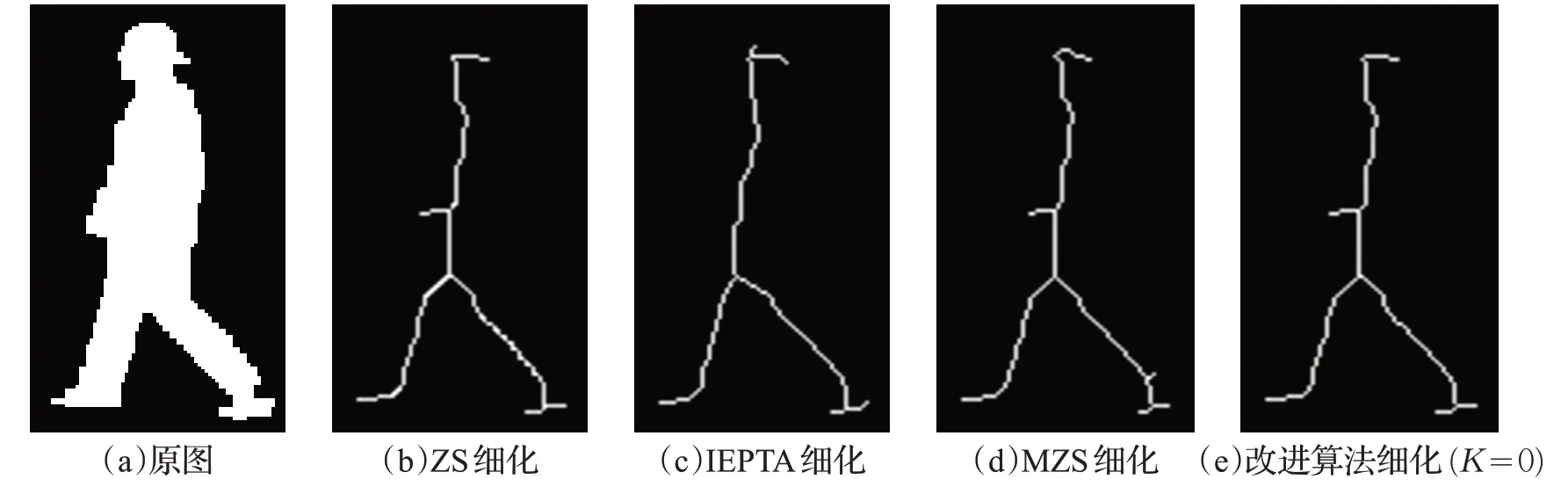
图10 人体结构细化效果对比

图11 字母结构细化效果对比

图12 仿真实验细化图片示例对比

如图11 所示，对字母图片进行细化处理后，ZS 算法、IEPTA 算法、MZS 算法的效果图均出现端点和边缘处的较大分叉。受到不平滑轮廓的干扰，未加入平滑迭代的改进算法也出现了边缘分叉，通过取一定大小的K值，有效去除了上下两处分叉，同时整体的骨架更加光滑。

以上4组图片的实验结果分别展示了改进算法对4类问题的展示效果。为了对各算法的细化程度进行精确的评估，对MPEG7 图像数据集进行细化仿真实验，图12展示了仿真实验的一个示例。

用于细化的目标图像应该具有整体的线条化结构，且所细化目标应具有可提取的特征及一定的现实意义。细化性能往往受到图像大小和图像内容的影响。因此从全部1 402张二值图像中选取适合细化的527张图片作为仿真对象。同时，在细化仿真前，进行必要的滤波和形态学预处理[18]，首先对数据集中的原始图像进行背景像素点填充，使其符合模板匹配的要求。然后针对图像中大量存在的边缘噪声和孔洞结构进行适当的形态学开操作与闭操作[19]。定义细化率为算法细化过程中删除掉的前景像素点数占原有前景像素点数的比例，各算法细化率结果和冗余像素情况在表1～表3中给出。

表1 各算法细化率对比

表2 不同K 值下的改进算法细化率对比

表3 各算法冗余像素情况对比

表1 展示了ZS、IEPTA、MZS 以及改进算法(K=0)的细化率仿真情况，其中改进算法的细化程度最高，其细化率比前三种算法分别高出0.23%、0.05%、0.11%，说明改进算法能够高效滤除图像中的冗余信息。表2 比较了不同平滑迭代次数下的改进算法的细化率，验证了增大平滑迭代次数将会进一步提高其细化程度，同时能提高对轮廓噪声的改善效果。表3 表明改进算法的细化结果无冗余像素，很好处理了像素冗余与结构丢失的矛盾问题。

5 结论

本文针对二像素宽度斜线结构全删除、正方形结构丢失、大量斜线冗余像素存在以及不平滑轮廓带来大量分叉四类问题，在原始ZS 细化算法基础上引入了平滑迭代流程以及后续的扫描过程，并在其中加入保留模板和删除模板条件的判定。通过针对性地保留和删除一些特定的拓扑结构，有效保留了二像素宽度斜线结构和正方形结构，并完全删除了斜线上的冗余像素，引入的平滑迭代能有效减少骨架轮廓的噪声分叉。仿真实验数据表明，不引入平滑迭代阶段的改进算法的细化率相比ZS、IEPTA、MZS算法提高了0.05%～0.25%不等；而平滑迭代次数的增加，能进一步提高细化程度，减少大量的轮廓分叉，完整保留了目标图像的骨架信息和拓扑性。

本文解决了现有细化算法在细化过程中的局部结构丢失、冗余像素以及轮廓分叉的问题，但没有对具体细化背景下合理的平滑迭代次数的选取做出精准估算，同时受到匹配模板及平滑迭代次数的影响其算法的实时性并不稳定。后期将就确定自适应的K值以及提高算法实时稳定性做进一步研究，完善其改进算法性能。