邻域近似条件熵的特定类属性约简及启发算法
2020-12-26张贤勇姚岳松
牟 恩,张贤勇,姚岳松,邓 切
1.西南医科大学 医学信息与工程学院,四川 泸州646000
2.四川师范大学 智能信息与量子信息研究所,成都610066
3.四川师范大学 数学科学学院,成都610066
1 引言
粗糙集属性约简能够有效实施降维优化与规则推理[1]。传统“决策分类约简”追求所有决策类的全局优化,而Yao和Zhang[2]提出的“特定类约简”涉及特定类的局部优化,两类属性约简分别位于决策表的宏观高层与中观中层[3]。当前,特定类约简主要立足于经典粗糙集[4-5],故值得推广。邻域粗糙集推广了经典粗糙集,但相关属性约简集中于决策分类约简(如文献[6-7]),还未见特定类约简的报道。
信息度量广泛应用于不确定刻画与属性约简。对于经典粗糙集,苗夺谦[8]建立信息熵、条件熵、互信息体系,而条件熵刻画了属性约简[9-10]。对于邻域粗糙集,Hu等[11]建立对数函数信息体系进行特征选择,Chen等[12]提出邻域精度、邻域熵、信息粒度及相关粒化单调性,Chen等[13]利用联合邻域熵来设计基因选择算法,Yuan等[14]采用邻域熵变种度量来进行离群点检测;进而针对属性约简,谢玲玲等[15]提出近似条件熵来进行属性约简,张宁和范年柏[16]提出邻域(近似)条件熵来构建启发式属性约简,赵小龙和杨燕[17]提出邻域粒化条件熵来设计增量约简算法,姚晟等[18]基于邻域粗糙互信息来进行非单调属性约简。
本文拟从邻域近似条件熵的信息角度,构建邻域粗糙集的特定类约简。从经典条件熵推广后的邻域近似条件熵出发,分解提取关于特定类的邻域近似条件熵,证明信息粒化非单调性,建立特定类约简及其启发算法,并提供实例分析与实验验证。
2 邻域粗糙集及高层邻域近似条件熵
决策表NDT=<U,C,D >包括有限论域U、条件属性集C={c1,c2,…,cl}、决策属性集D。邻域体系涉及距离函数d与半径参数δ。本文采用Manhattan 距离可得邻域nC(x)={y∈U|dC(x,y)≤δ}、邻域关系NC={(x,y)∈U×U|dC(x,y)≤δ}、邻域覆盖U/NC={nC(x)|x∈U} 。任意条件属性子集B⊆C可以产生相关概念,如邻域采用nB(x)或(x)并设邻域粒数为n。设决策分类U/IND(D)={Dj|j=1,2,…,m}具有m个决策类。
定义1[7]决策类Dj关于B⊆C的邻域上下近似为:

基于文献[8-9,15-16],下面自然建立邻域(近似)条件熵,其中邻域及其粒数采用不重复规则,有利于覆盖粒结构推理;当覆盖退化到划分时,它们将退化到经典粗糙集的(近似)条件熵。
定义2 决策属性集D相对于B⊆C的邻域条件熵为:


邻域条件熵CE(D|B)采用经典条件熵公式,将等价剖分结构泛化推广到邻域覆盖结构,具有相应不确定性语义。邻域近似条件熵ACE(D|B)引入邻域近似粗糙度ρB(Dj)作为权重系数,有效融合覆盖结构信息与近似逼近信息,变得更为强健。
3 中层邻域近似条件熵
上述高层邻域(近似)条件熵适用于整个决策分类。下面对它们施行“求和换序”与“分解提取”,得到中层相应概念,以适用于特定决策类。
定义3 决策类Dj相对于B⊆C的邻域条件熵为:

中层邻域条件熵CE(Dj|B)对所有不重复邻域粒实施信息集成,表征邻域覆盖结构对于特定决策类的不确定性程度。基于信息融合[15-16],ACE(Dj|B)集成了信息度量CE(Dj|B)与结构度量ρB(Dj)的不确定性信息,有效用于邻域粗糙集的特定类约简构建。下面揭示CE(Dj|B)、ACE(Dj|B)的上下界与粒化非单调性。为此,提取定义3公式内层,记

定理1(1)CE(Dj|B)∈[0,|Dj|lb|U|]、ACE(Dj|B)∈[0,|Dj|lb|U|] 。(2)若BndB(Dj)=∅,则CE(Dj|B)=0 、ACE(Dj|B)=0 。(3)若U/NB={U} 且Dj={x}⊂U,则CE(Dj|B)=(1/|U|)lb|U|、ACE(Dj|B)=(1/|U|)lb|U|。
证明(1)对特定类Dj,若邻域)满足)⋂Dj=∅则p(Dj|))=0、CE(Dj|))=0。下面考虑交Dj的邻域并,设Sj={i∈{1,2,…,n}x)⋂Dj≠∅}则|Sj|≤n≤N(这里N=|U|)。 ∀i∈Sj有p(Dj|))∈[1/N,1]与lbp(Dj|))≥lb 1/N。因此:
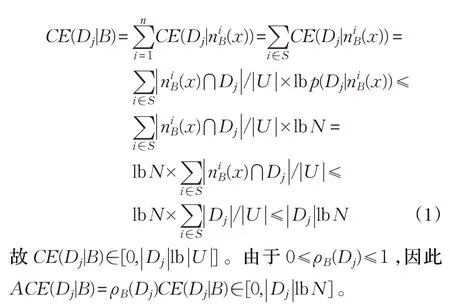
(2)若BndB(Dj)=∅,这意味着∀nB(x)∈U/NB,nB(x)⋂Dj=∅、p(Dj|nB(x))=0 或nB(x)⋂Dj=nB(x) 、p(Dj|nB(x))=1,即CE(Dj|nB(x))=0。从而CE(Dj|B)=0;进而ACE(Dj|B)=0,其中ρB(Dj)=0。
(3)若U/NB={U} 且Dj={x}⊂U,即只存在唯一邻域U,且其满足p(Dj|U)∈(0,1)、lbp(Dj|U)=lb(1/N),根据公式(1)有CE(Dj|B)=(|Dj|/|U|)lb|U|=(1/|U|)lb|U|。进而ACE(Dj|B)=(1/|U|)lb|U|,其中ρB(Dj)=1。
定理2 设属性子集A,B⊆C诱导的邻域覆盖U/NA、U/NB具有粒化关系U/NA-≺U/NB(即∀x∈U有nA(x)⊆nB(x)),则CE(Dj|A)与CE(Dj|B)、ACE(Dj|A)与ACE(Dj|B)无必然大小关系。
证明因为U/NA-≺U/NB有nA(x)⊆nB(x) 。该嵌套邻域结构与决策类Dj具有三种相交情况。
(1)若nA(x)⋂Dj=nB(x)⋂Dj=即p(Dj|nA(x))=p(Dj|nB(x))=0,则可以得到:

(2)若∅=nA(x)⋂Dj⊆nB(x)⋂Dj则0=p(Dj|nA(x))≤p(Dj|nB(x))≤1。由于上凸函数-plbp的非单调性,不能确定p(Dj|nA(x))×lbp(Dj|nA(x))与p(Dj|nB(x))×lbp(Dj|nB(x))的大小关系。从而,也不能确定CE(Dj|nA(x))与CE(Dj|nB(x))大小关系。
(3)若∅⊂nA(x)⋂Dj⊆nB(x)⋂Dj,但两个非0 概率p(Dj|nA(x))与p(Dj|nB(x))之间的大小不确定[18],故CE(Dj|nA(x))与CE(Dj|nB(x))大小关系也是不确定的。
综上,CE(Dj|nA(x))与CE(Dj|nB(x))无必然大小关系。后续粒化结构的重复计数消除过程也具有不确定性,故基于U/NA与U/NB结的CE(Dj|A)与CE(Dj|B)无必然大小关系。进而,ACE(Dj|A)与ACE(Dj|B)也无必然大小关系。
4 基于邻域近似条件熵的特定类属性约简
基于中层邻域(近似)条件熵及其不确定性语义、粒化非单调性,本章构建相应的特定类属性约简及其启发算法,主要采用具有信息修正的邻域近似条件熵。
定义4 基于邻域近似条件熵,B⊆C称为C相对于决策类Dj的一个约简,若如下两条成立:

这里的约简目标追求更大的邻域近似条件熵值,这种单向方案已经实际使用[18]。定义中的两条分别对应“联合充分性”与“个体必要性”。接下来,类似于文献[18],引入属性重要度并构建启发式约简算法。
定义5a∈B关于B的内属性重要度为:

内重要度sigin(a,B,Dj)表示在B中删除属性a产生的关于邻域近似条件熵的信息减量,而外重要度sigout(a,B,Dj)表示在B上增加属性a产生的信息增量,两者提供了快速约简的属性选择机制。若a关于B是重要的,那么邻域近似条件熵满足关系ACE(Dj|B)>ACE(Dj|B-{a}), 因此sigin(a,B,Dj)>0, 反之sigin(a,B,Dj)<0 ;对于a∈(C-B) ,若a关于B是重要的,则ACE(Dj|B⋃{a})>ACE(Dj|B),因此有sigout(a,B,Dj)>0,反之sigout(a,B,Dj)≤0。由此,下面采用这两种重要度来设计一个启发式搜索算法,以快速得到一个特定类约简。
算法1 基于邻域近似条件熵的特定类属性约简启发算法。
输入 决策表NDT=<U,C,D >,邻域半径δ;
输出 基于邻域近似条件熵的特定类约简R。
步骤1 设置R=。
步骤2 计算∀a∈C的内属性重要度sigin(a,C,Dj),满足sigin(a,C,Dj)>0 的属性a均加入R(即实施循环更新R←R⋃{a})。
步骤3 计算子集R与全集C关于特定类Dj的邻域近似条件熵ACE(Dj|R)与ACE(Dj|C)。若ACE(Dj|R)≥ACE(Dj|C),则进入步骤5,否则进入步骤4。
步骤4 计算∀a∈(C-R)的外属性重要度sigout(a,R,Dj),并选择属性重要度最大的属性a*并入R(即施行一次更新R←R⋃{a*}),并进入步骤3。
步骤5 ∀a∈R,若属性a满足ACE(Dj|R-{a})≥ACE(Dj|R),则从R中删除a(即采用循环更新R←R-{a})。
步骤6 返回R。
算法1 优化了文献[18]的非单调性算法结构,并主要采用邻域近似条件熵。步骤1是初始化。步骤2是启发搜索过程,主要在条件属性全集C中选取对类Dj具有相关模式识别功能的属性。步骤3是一个评估过程,若步骤2 得到的子集R的邻域近似条件熵小于全集C的(即ACE(Dj|R)<ACE(Dj|C)),则需要利用步骤4 进行剩余属性的启发式搜索,并加入最优属性以快速完成添加。可见,邻近步骤5 的R必然满足约简“联合充分性”,但不一定满足约简“个体必要性”。由此,步骤5采用反向冗余删除,最终获得约简“个体必要性”。基于文献[18]的算法分析过程与结果,这里的算法1 计算量仍旧主要集中在步骤2,因此整个的时间复杂度为O(|C||U|lb |U|)。该算法是有效的,能够得到一个基于邻域近似条件熵的特定类属性约简。
5 决策表实例
本章提供一个实例,说明度量性质与属性约简。决策表NDT=<U,C,D >如表1,其包括两个决策类:D1={x1,x2}、D2={x3,x4}。

表1 实例决策表
基于Manhattan 距离与邻域半径δ=0.4,下面聚焦属性增链

该链诱导出邻域覆盖及其粒化关系:

由此,可得两个特定类的邻域粗糙度:

上述所有值均隶属理论双界范围[0,|Dj|lb |U|=4](定理1)。4个不等式验证了粒化非单调性(定理2)。
最后分析特定类约简,主要采用决策类D2来说明算法1。步骤1 赋值R=∅。步骤2 计算3 个条件属性的内重要度:

由此没有属性满足加入条件sigin>0,故R=∅。此时R达不到约简第一条,在步骤3 中判断后需要转入步骤4,计算3个条件属性的外重要度:

基于最大值随机选取一个属性如c1并入R,有R={c1}。此时,用更新的R={c1}进入步骤3,检验有:

即{c1} 满足约简第一条从而进入步骤5。基于步骤5,单属性c1不能被删除,即{c1} 满足约简条件第二条,并最终在步骤6中输出作为约简结果。
6 UCI数据实验
本章实施数据实验来验证邻域(近似)条件熵及其特定类约简,主要是粒化非单调性(定理2)与启发式约简算法(算法1)。下面从UCI 机器学习知识库(http://archive.ics.uci.edu/ml)中选取5 组数据集,如表2。首先采用最大-最小标准化数据预处理,仍用Manhattan距离函数,邻域半径参见表2。

表2 5类UCI数据集的基本描述
为表现度量变化,特选取自然属性增链{c1}⊂{c1,c2}⊂…⊂C。针对所有的13 个决策类,进行了完全实验计算;这里提供代表呈现,对此前3 个数据选取D2而后2 个数据集选取D1,相关度量结果参见图1。在图1 中,横坐标整数标识属性增链元B,纵坐标实数标识邻域条件熵CE(Dj|B)、邻域近似精度αB(Dj)(即1-ρB(Dj))、邻域近似条件熵ACE(Dj|B)。观测可见,αB(Dj)很接近于0,CE(Dj|B)与ACE(Dj|B)具有细微调整差距,它们的粒化非单调性非常明显。基于这些非单调变化曲线,追求邻域近似条件熵大值的特定类约简是合理的,其可以得到适当长度的约简结果。
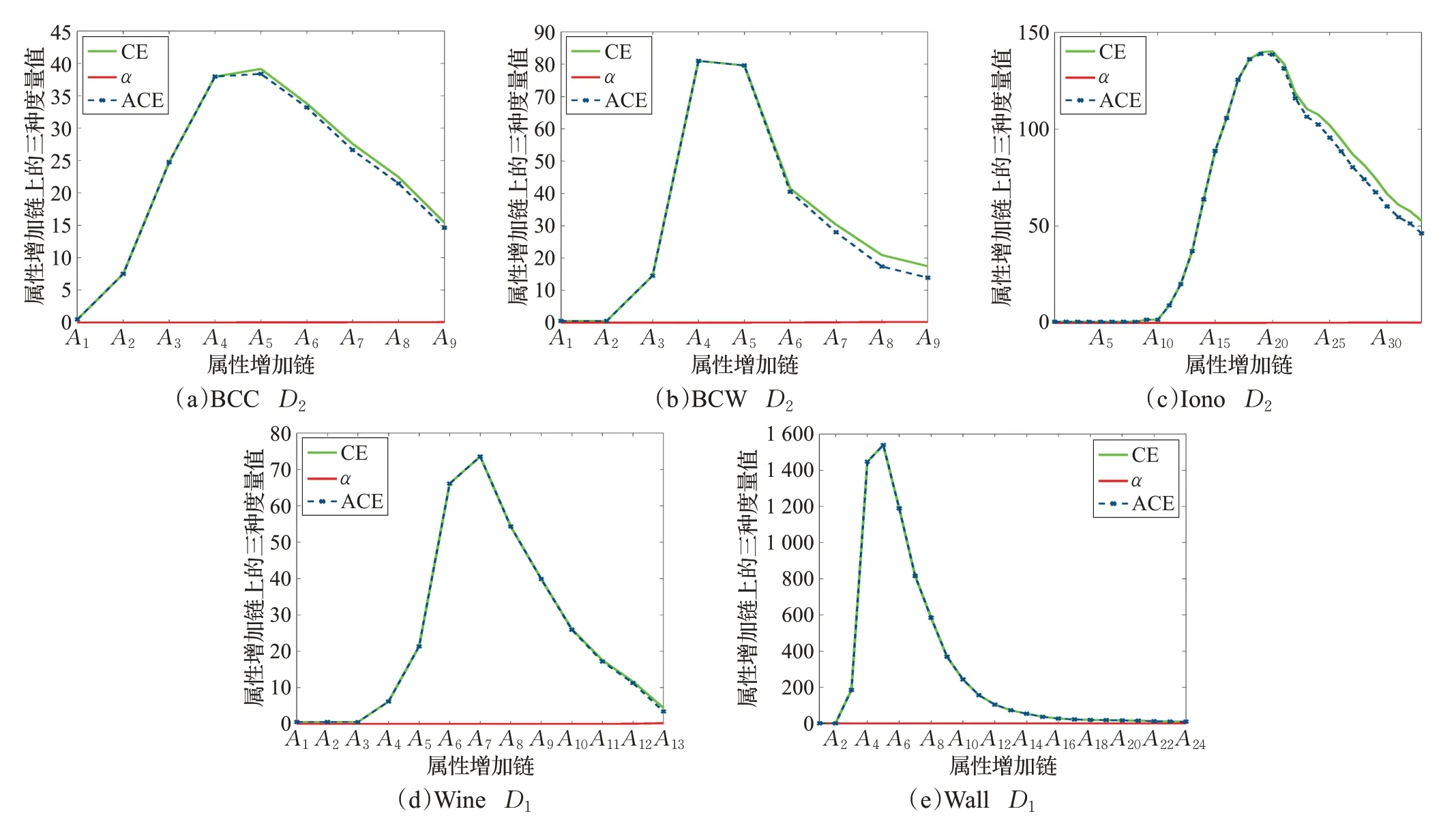
图1 5类UCI数据集关于属性增链的三种度量变化
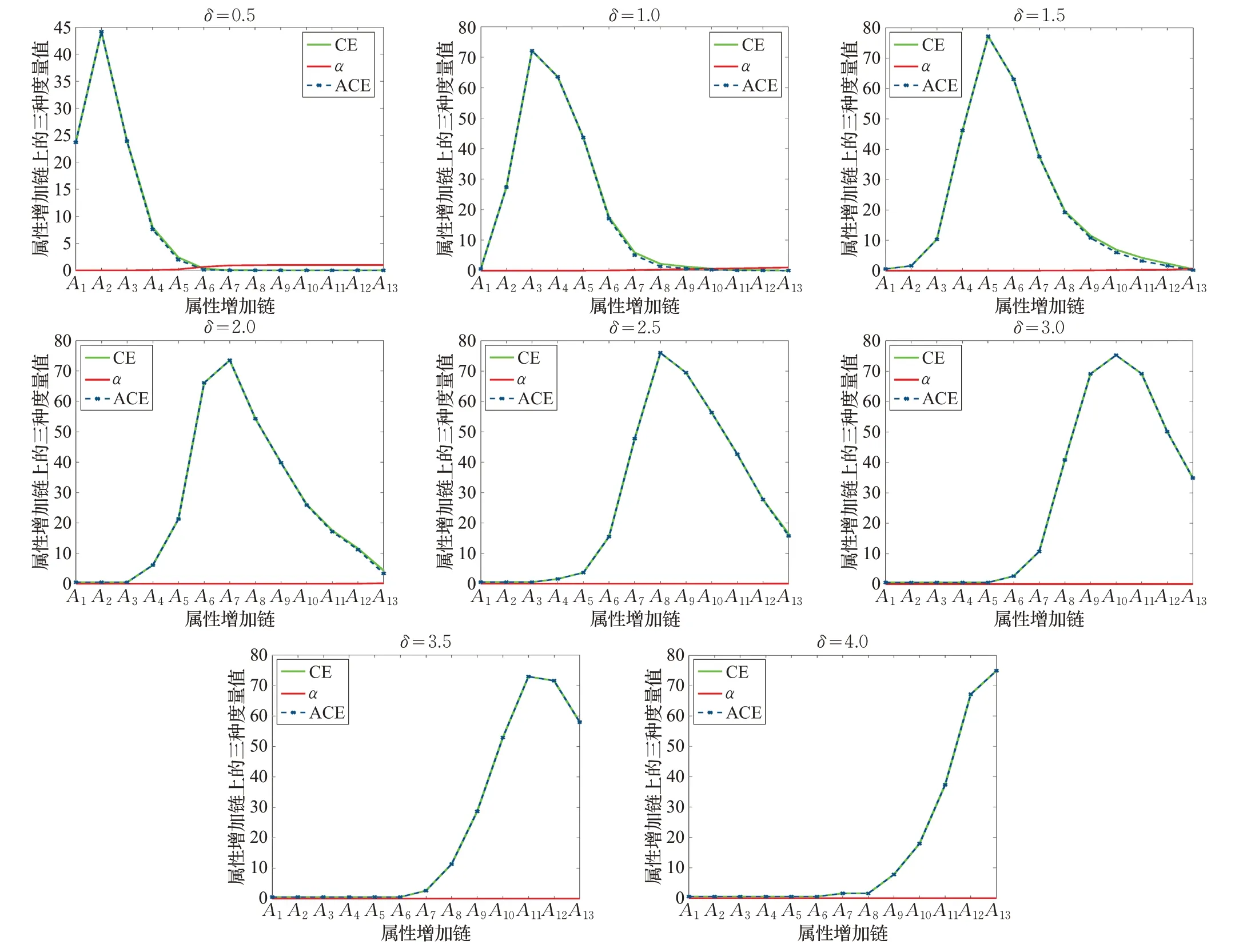
图2 Wine数据集D1 类关于属性增链与半径增链的三种度量变化
最后分析邻域半径对度量与约简的结果影响。作为代表,选取数据集Wine 的D1类,以δ=0.5 为初始值并以0.5 为步长构造半径增链。图2 提供了CE(Dj|B)、αB(Dj)、ACE(Dj|B)在半径增链与属性增链上的变化。基于图2,对于邻域近似条件熵,通常的半径能够较好表现粒化非单调性,而波峰或最大值随着半径增大而右移;可见,半径取值决定着度量数值以及后续约简。
进而,表3提供了特定类约简结果,验证了算法1的有效性。表4 则提供了Wine 数据集D1类相关半径增链的约简结果。基于表4,约简具有随半径变大而属性增多的大体趋势;邻域半径过小(如0.5)会导致属性约简太单一,半径过大(如4.0)则约简太冗余,即这两种极端情况下的约简结果都不太理想;当δ取2.0、2.5、3.0时,约简结果较好。此外,其他数据集实验都表现出类似结果,即适中的邻域半径能够有效表现粒化非单调性并获取较好属性约简,而表2中的半径取值正是经过实验分析所得的较好参数设置。

表3 5类UCI数据集的特定类约简

表4 Wine数据集D1 类关于半径增链的约简
7 结束语
本文粒化分解决策表高层的邻域(近似)条件熵,提取出中层的邻域(近似)条件熵,获得信息上下界与粒化非单调性,进而构建特定类属性约简及其启发式约简算法。本文构建邻域(近似)条件熵深化了文献[15-16]的相关度量,后续特定类属性约简推广了文献[2]的经典特定类约简,而相关启发式约简算法模拟并优化了文献[18]的算法。所得结果有利于特定类模式识别的不确定性度量与优化应用,值得深入探讨。
