节点传播能力的偏好随机行走的信息传播方法

李维勇，孔 枫，张 伟，陈云芳

1.南京信息职业技术学院 网络与通信学院，南京210023

2.南京邮电大学 计算机学院，南京210023

1 引言

近年来，随着社交网络的发展，对于社交网络中的信息传播的研究一直很活跃。在实际的在线社交网络中，用户活动一直是呈现出爆炸式的增长的，例如在Facebook、Twitter 和Google+这些网络和微博中，十几亿的用户每天都处在分享热点信息的过程中。使用这些交流工具，人们可以和世界各地的朋友和追随者在圈子中交流想法、观点、视频和照片等等。这些互动产生了空前的数据量，这些数据量可以作为衡量社交的观察容器，并通过定量的方法来阐明人类社交的交流机制[1-6]。

如何在复杂的社交网络中找到最大的传播范围已成为许多领域的热门话题，包括社会学、生物信息学和物理学。目前关于社交媒体的研究主要包含2个主题：传播以及它的社会网络结构。大多数网络模型都将重点放在系统的结构增长（称之为网络的动态）或信息传播过程（在网络上发生的动态）上。社交网络中的节点往往具有共同的兴趣或背景，那么当热点信息吸引网络中的用户时，会导致网络中的信息以一定的规则在用户中进行传播，这些被传播的网络用户集合可以简化对整个网络的功能分析。

现有的很多模型都在描述消息的传播过程，例如独立级联模型[7]、线性阈值模型[8]、基于数据的信用分部模型[9]和线性社交影响模型[10]等。在这些模型中，独立级联模型和线性阈值模型是随机扩散模型。上述模型中的节点只存在两种状态：活跃和非活跃。活跃节点可以被视为接受了这条消息并会再次传播这条消息的节点；而非活跃节点则是未被激活且不会传播这条消息的节点。然而，在实际传播中非活跃节点也存在两种类型。例如，对于一条发布在Twitter 上的消息，有些用户会转发这条消息，有些用户则不会。但是在没有转发的用户中，有些人由于邻居节点的转发而得知了这条消息成为消息节点，其余节点为真正的非活跃节点。可以推断，一个节点想要成为消息节点，那么它的邻居节点中至少有一个为活跃状态；相反，如果一个节点的全部邻居节点都为非活跃状态，那么此节点永远不可能成为消息节点。现实世界中消息节点的数量非常庞大，但是由于影响力最大化问题只考虑活跃节点而忽略了消息节点，所以它不能很好地模拟现实世界。为了更好地衡量信息覆盖范围，应将这两类不会再次传播消息的节点都列入考虑范围。因此，考虑从非活跃节点中找出消息节点，并发掘消息节点的价值，以更好地衡量信息覆盖范围。

而随机行走是一种不规则的、布朗运动的数学理想状态，在许多领域都有重要的应用，其中在计算机领域一个很有名的例子就是Google的PageRank算法。近年来，在信息传播领域中加入了一种基于随机行走的概率方法，但是当随机行走偏向于远离稳定状态所占的区域方向时就产生了一个有趣的问题，在什么条件下传播速率和偏向会导致传播的结果停滞不前呢。或者从相反的方向来说，当普通的随机行走在不同的方向上具有偏差时，维持正常的传播速率的偏差临界值是多少呢。因此，本文提出了一种基于节点传播能力的偏向性随机行走的信息传播方法，该方法的创新性体现在以下3个方面：

（1）将每个节点的信息传播能力，即网络中节点能承受的传播的信息的内容量，纳入信息传播的关键因素。

（2）提出了一种新的随机行走方法，即偏向性随机行走，通过偏向性参数来控制随机行走的方向，使得随机行走不再是漫无目的的无规则行走。

（3）利用以上两个参数结合作为衡量节点成为活跃节点和消息节点的重要属性，得到信息传播范围最大化函数来使得活跃节点和消息节点的集合达到最大。

2 相关研究

随着社交网络的发展，对于信息传播模型的研究一直很活跃，社会网络是由许多节点构成的一种社会结构，节点通常是指个人或组织，商业领域中的“口碑营销”是社会网络中重要的应用场景，该种形式同样适用于信息和影响力的传播过程，因此，社会网络在信息的传播中起到至关重要的媒介作用[11]。其中通过在社会网络中找到一个具有一定影响力的个体组成的小群体继而能够影响社会网络中数量最多的人是以“口碑”[12-15]形式的信息传播的根本目的。

Gomez 等[16]提出了依据激活节点和其每个邻居节点之间的相关性，从而推断出传播级联的结构。假设活跃的节点以一定的概率影响其每个邻居节点，并且节点之间是相互独立的影响，他们称其为NETINF方法。该方法构建一个概率模型，该模型需要解决在一个固定的假想网络中，级联是如何作为有向树来传播的（扩散级联即在一棵有向树中，激活序列的第一个节点称其为有向树的根节点，由于一个网络中的节点不会被重复感染，所以消息传播的路径中不存在回路，此时的消息传播就可以被视为一种有向树的传播形式）。

后来Gomez 等人又扩展了NETINF 算法[17]，称为NETRAT 算法，通过观察传染性来推断底层传播的过程，传播的过程发生在未知的网络图中，节点是否感染只有2种状态（1或0），即一个节点受到感染或未受到感染，不存在部分感染或信息的部分传播概念，感染发生在不同的时间并且沿着网络的边彼此独立的发生，最终推断网络的连通性，以及观察节点被感染后，推断通过边传播的可能性。

为了能够观察到网络的动态变化，如网络的边和边的动态变化，Gomez 等人又扩展了NETRAT 算法，提出了一个随时间变化的推论算法——INFOPATH[16-17]，这种算法使用随机梯度来提供网络结构的在线估计和随时间变化的状态，它记录了节点感染时间和传播的事件，允许信息通过数据驱动的方法以不同的速率在网络中不同的边缘传播。

Saito等人提出了AsIC模型[18]，解决IC模型和LT模型存在的一个问题，它们把信息传播看作是节点的一系列状态变化，而实际的传播是沿着连续时间轴以异步方式进行，并且观察到的数据的时间标记并非等距。

Guille 等人为在一个封闭环境中，用户通过社交网络交互，如何模拟这种环境并且预测传播特性，提出了T-BaSIC模型[19]，它主要考虑传播扩散过程的时间动态，能够从一种更实际的角度出发通过机器学习的算法建立模型，预测社交网络的信息传播过程。它假设社交网络中的信息传播依赖于用户之间的连接图，并且是根据局部特性由节点之间的微相互作用解释的。之后根据图中个人的行为进行统计分析，而非全局行为。

Leskovec 等为找到最简单、直观的模型，并且参数尽可能少的模型，提出了一个简单而直观的SIS 模型[20]（其中S 代表“敏感（或易感染）”，I 代表“感染”（接受了某信息），在SIS 情况下，在I 状态的节点会以固定概率变回状态S），仅需要一个参数。它假定所有节点都以相同的概率β被感染（激活），被感染的节点在下一时间段重新成为敏感节点。

在许多情况下，网络上发生的传播行为实际上是隐式的，甚至是未知的。Yang等人[21]为面对现实世界中的网络进行建模，提出了一种LIM 模型，它关注于模拟一个节点对全局的影响力，而不是预测哪个节点会感染其他节点，或是节点感染哪一个节点。它虽忽略时间和在离散时间段内的工作，但是准确模拟了每个节点的影响力并且描述了整个传播扩散过程。

本文提出了一种基于节点传播能力的偏向性随机行走的信息传播模型，该模型结合了IC模型，与IC模型不同的是，一个节点w在第t被激活，其中v节点是w节点的某个邻接点，当节点v的活跃邻居节点w尝试激活节点v时，即使没有激活成功，v节点也会得到该消息，故称v节点为消息节点。另外还加入了节点传播信息的能力，更加符合真实的社交网络交往。

3 偏向性随机行走的定义

图上的随机行走是马尔科夫链的一个子类，传统的方法都是用来处理无偏向随机行走特性以及计算与网络相关的转移概率，一般使用G=(V,E)来表示一个网络图，其中V={v1,v2,…,vn} 和E={e1,e2,…,en} 分别表示节点集合和边的集合，图G的邻接矩阵为W ，其中wij=1 表示节点i和节点j之间存在连接的边，wij=0 表示不存在。在这里图G被认为是无向网络图，所以邻接矩阵W 是对称矩阵。d(i)=表示节点i的邻接点的个数。根据随机行走是由一系列无规则的步数形成的路径的数学化形式，假设节点i的邻接点是节点j，那么节点i到节点j一步转移概率即为Pij，此时Pij=为图G的无偏向性随机行走的一步转移概率矩阵。

在真实的社会网络中，不同的节点所具有的重要性也不相同，这就导致了每个节点也具有不同的传播能力。很多文献在研究社区结构的发现和信息传播的过程中，会倾向于先通过某些方法去寻找社会网络中的某些节点，这些节点在社会网络中有着一定的影响力，例如：Saito等人[22]就是通过社会网络中具有的特定社区结构，从而发现了k个最具影响力的节点，他们认为这k个最具影响力的节点会使得网络中信息传播的范围达到最大化，但是在信息传播的过程当中，社区中还有一些节点往往是不可忽视的，和那些具有影响力的活跃节点相比，即使它们的传播能力可能较弱，然而往往这些节点在信息传播的过程中起着至关重要的作用。因而，与其耗费大量的时间去寻找网络中最具有影响力的节点，不如随机在网络中选择任意一个节点作为传播源，故基于现实的社交网络，假设存在任意的一个传播源节点a,m表示它的所有邻接点的个数，K={k1,k2,…,km}是邻接点度的集合，k1,k2,…,km分别是a的邻接点的度，根据偏向性随机行走的机制[23]，定义偏向性随机行走的转移概率为：

其中，节点i为传播源节点a的其中一个邻接点，Pai为节点i成为活跃节点或者消息节点的概率；α为偏向性随机行走的控制参数。当α=0 时，所有邻居节点都有平等的机会接收从节点a传播过来的信息，这意味着它们被传播到的可能性相同。当α＞0 时，度数较大的节点更有可能接收到被传播的信息，当α＜0 时，度数较小的节点更有可能接收到被传播的信息。

4 DCID算法

社交网络影响力最大化研究，其目的是选择一组种子节点，使得传播结束后获得的活跃节点数最多，达到影响范围最大化。但是最后的活跃节点数并不能完全代表真实的信息覆盖情况。一种常见的情况是，当某个节点的活跃邻居节点尝试激活它时，即使没有激活成功，该节点也会得到该消息，故称之为消息节点。因此，当研究社交网络中信息覆盖最大化时，除了需要考虑活跃节点的数量，消息节点的影响也不能忽略，进而产生了信息覆盖最大化的问题，这个问题的目的是找到最多的活跃节点和消息节点。

在本文中，每一次一个被传播到的节点通过偏向性随机行走将连续不断地发送C个要传播的信息给它的邻接点，如果一个节点已不具有消息节点或者活跃节点的价值，那么该节点将永远不会被激活。如果一个节点接收到了被传播的信息C，那么它会将该信息C在下一步继续传播下去。在已经成为消息节点和活跃节点的这些节点中，依然会有某些节点有λ的概率被重复传播，那么这些被重复传播的节点应该被剔除。

对于传播源节点a，每次传播信息C，节点i无法被传播到的概率为：

假设Xi是一个随机变量，代表节点i被传播到的事件，Xi=0 表示节点i完全没有从节点a收到任何传播信息，Xi=1 表示节点i从节点a至少收到了一条被传播的信息：

假设一个随机变量Y代表被节点a传播到的邻接点的个数的事件，得到Y的平均值为：

其中，m是指节点a的所有邻接点，但是在信息传播的过程中，节点a的邻接点并不仅仅是易被传播的节点，为了有效地估计被节点a传播到的邻接点个数，还需要知道在节点a的所有邻接点中容易被传播到的节点的个数，为了估计在t步随机行走后被传播到的所有节点的个数，计算网络中被传播到节点的邻居节点中易被传播节点的个数为：

其中，nj是被传播到的节点j的邻居节点中易被传播节点的个数，I(t)表示节点j的邻居节点在t步随机行走之后被传播到的节点个数，N(t)表示在t步随机行走之后，被传播到的所有节点的邻接点中易被传播到的节点个数，那么t步随机行走后，被传播到的节点总数为：

算法1记录了DICD算法的整个过程，首先，在整个网络图中选择一个初始的传播源节点，然后根据公式（3）用偏向性随机概率以及节点的信息传播能力衡量一个节点是否能够成为消息节点或者是活跃节点，最后根据公式（8）利用信息传播最大化函数使得网络中的消息节点和活跃节点的集合达到最大。

算法1 信息传播最大化

输入：图G，初始传播源节点a，被传播节点的传播能力C，偏向性随机行走参数α

输出：消息节点和活跃节点总和I

1. for a do

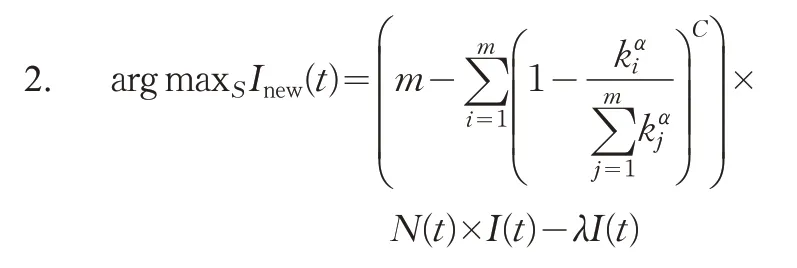
3. End for

4. 输出I

从公式（8）中很明显可以看出，被传播节点的传播能力C是本文的关键参数，已被传播到的活跃节点或消息节点的传播能力越大，那么易被传播的节点被传播的可能性就越大。参数α是本文传播模型中的另一个关键因素，它决定了当传播能力C是一个有限常数时被传播到的节点（即已成为活跃节点或消息节点）的邻居节点被传播的可能性。

5 实验分析

实验采用的电脑是英特尔第八代酷睿处理器，内存为16 GB DDR3，Windows 10 操作系统以及Matlab R2012a数据分析工具。

为验证本文提出的DCID 算法的准确率以及算法运行时间，实验选用Facebook 网络以及Google+网络，这2 个网络都是描述人与人之间关系的友谊网络，其中节点表示用户，边代表用户与用户之间的关系，在Facebook网络中包含了2 888个节点和2 981条边；其次选用Google+网络作为大规模社交网络，它包含了23 628个节点和39 242 条边。使用1，2，3，…，来对网络Facebook网络以及Google+网络进行节点进行编号。通过与KK（Kemple 和Kleinberg，KK）算法[24]以及ICGreedy算法[25]进行对比，验证本文提出的DCID 算法在准确率和运行效率上有所提升。

5.1 确定随机行走的偏向性参数

本文中，根据公式（8）可以看出信息传播最大化的关键在于2个参数，被传播节点的传播能力C以及偏向性随机行走的参数α，下面对传播能力C以及偏向性随机行走的参数α进行选取。

从Facebook 网络中随机选取一个节点作为信息传播源，然后利用公式（8），对公式（8）用微积分的方式进行求解最大化问题，公式（8）转化为：

为了使传播的曲线更加平滑，选取λ=0.05，然后从被传播节点的传播能力C以及偏向性随机行走的参数α两个方面分别对Facebook 网络进行这2 个参数的选取，首先选取了C=1,α=-1、C=1,α=-5、C=1,α=-10 以及C=1,α=-15 得出在Facebook 网络中信息传播的范围，如图1所示。

图1 Facebook网络中C=1 对应的不同α 值的传播范围

从图1 中可以看出C=1,α=-10 时信息传播的范围最大，但是由于无法从一种固定的参数选取中确定这2 个参数的值，因此又选取了C=2,α=-1、C=2,α=-5、C=2,α=-10 以及C=2,α=-15 得出在Facebook网络中信息传播的范围，如图2所示；最后选取了C=5,α=-1、C=5,α=-5、C=5,α=-10 以及C=5,α=-15得出在Facebook网络中信息传播的范围，如图3所示。

图2 Facebook网络中C=2 对应的不同α 值的传播范围

图3 Facebook网络中C=5 对应的不同α 值的传播范围

从图1、图2 和图3 可以看出，首先C的值越大，信息传播的范围会越来越小，即当节点传播的信息量越大时，随着随机行走的步数增加时信息传播的范围会越来越小；其次在节点具有同样的传播能力下，当α=-10时，随着随机行走的步数增加，信息传播的范围达到最大。此时在Facebook网络中选取的参数为C=1,α=-10。

下面在大型网络Google+网络中用同样的方法来进行参数的选取，利用公式（8），同样选取λ=0.05，从被传播节点的传播能力C以及偏向性随机行走的参数α两个方面分别对Google+网络进行这2 个参数的选取，首先是选取了C=1,α=-1、C=1,α=-5、C=1,α=-10 以及C=1,α=-15 得出在Google+网络中信息传播的范围，如图4所示。

图4 Google+网络中C=1 对应的不同α 值的传播范围

同时又选取C=2,α=-1、C=2,α=-5、C=2,α=-10 以及C=2,α=-15 和C=5,α=-1、C=5,α=-5、C=5,α=-10 以及C=5,α=-15 得出在Google+网络中信息传播的范围，如图5和图6所示。

图5 Google+网络中C=2 对应的不同α 值的传播范围

图6 Google+网络中C=5 对应的不同α 值的传播范围

从图4、图5 和图6 中可以看出，在Google+网络中同样是随着随机行走的步数增加，C的值越大，信息传播的范围会越来越小；其次在节点具有同样的传播能力下，当α=-10 时，随着随机行走的步数增加，信息传播的范围达到最大。因此通过在中等网络以及大型网络的实验中，确定出被传播节点的传播能力C=1 以及偏向性随机行走的参数α=-10。

但是此时只能确定被传播节点的传播能力C=1 时的确是能够使得信息传播的范围达到最大，但是上文中提到当α＞0 时，度数较大的节点更有可能接收到被传播的信息，当α＜0 时，度数较小的节点更有可能接收到被传播的信息。α=-10 只能说明此时度数较小的节点更有可能接收到被传播的信息，所以同样也要选取α＞0 时的信息传播的范围，如图7和图8所示。

图7 Facebook网络中不同α 值对应的传播范围

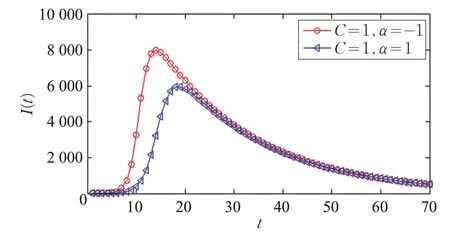
图8 Google+网络中不同α 值对应的传播范围

从图7 和图8 中可以看出，当C=1，α=-1 时，信息传播的范围比α=-1 时信息传播的范围更小，此时，才能真正确定出被传播节点的传播能力C=1 以及偏向性随机行走的参数α=-10 时，在Facebook 网络中和Google+网络中的信息传播范围达到最大。

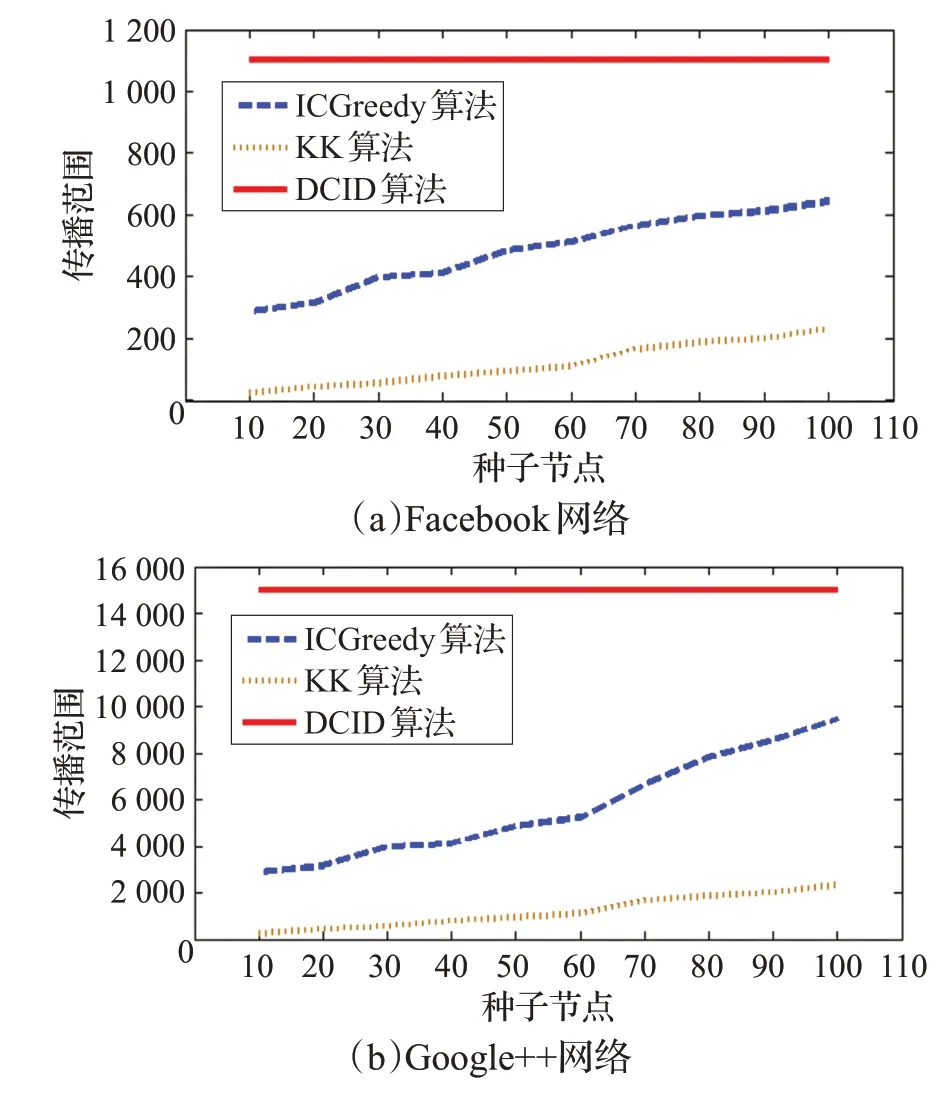
图9 DCID算法和其他2个算法的传播范围对比

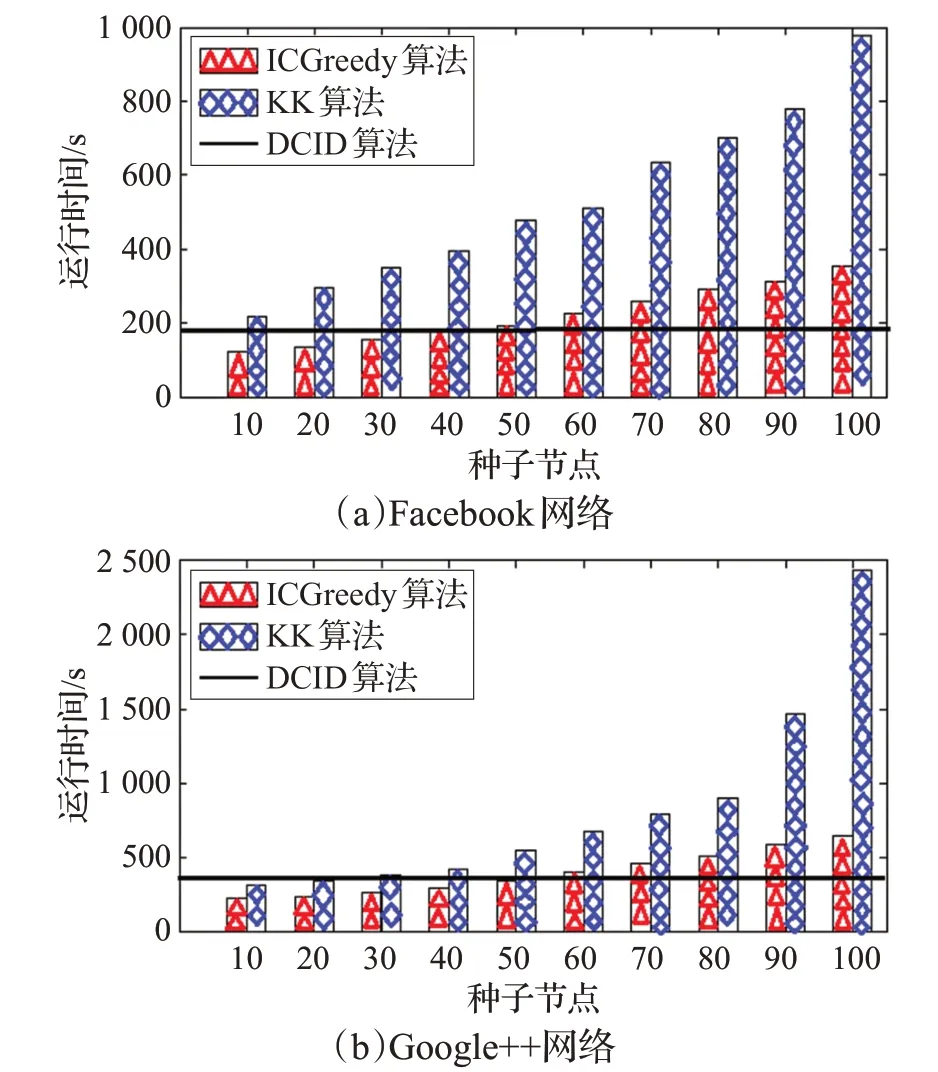
图10 Facebook网络、Google+网络中三种算法的运行时间对比

5.2 算法的精确率

由上文中选取的参数确定的传播范围，将本文算法和KK算法以及ICGreedy算法分别在Facebook网络中和大规模的Google+网络进行传播范围的对比，如图9所示。

由于本文算法和初始的种子节点无关，所以选取在DCID 算法传播范围最大的情况下和ICGreedy 算法以及KK算法进行对比，图9（a）记录了在Facebook网络中不同的初始种子节点下，KK 算法、ICGreedy 算法和DCID算法的传播范围，从图9（a）中可以明显地看出，随着初始种子节点的数量增加，DCID 算法的传播范围已远远超过KK算法、ICGreedy算法的传播范围。图9（b）记录了在Google+网络中不同的初始种子节点下，KK算法、ICGreedy算法和DCID算法的传播范围，同样地，从图中可以看出DCID算法的传播范围明显优于KK算法和ICGreedy算法。

此外，还比较了本文算法和ICGreedy算法以及KK算法的运行时间，图10记录了在Facebook网络和Google+网络中三种算法的运行时间，从图10中可以看出，由于本文提出的DICD算法与初始的种子节点无关，所以选取了本文算法在两种不同规模的网络中达到传播范围最大时的运行时间与ICGreedy 算法以及KK 算法的运行时间进行对比，因而，从图10中看到在Facebook网络和Google+网络中的运行时间没有发生改变，是一条没有波动的直线。图10（a）记录了在中等规模Facebook网络中ICGreedy算法和KK算法与DCID算法的运行时间的对比，ICGreedy算法和KK算法在随着初始节点增加的情况下，运行的时间也随之增大，初始种子节点个数小于40的情况下，本文的算法优势并不明显，运行的时间略大于ICGreedy算法，但始终低于KK算法的运行时间，随着初始种子节点个数不断增加，ICGreedy 算法和KK算法的运行效率明显低于本文算法。图10（b）记录了在大规模Google+网络中ICGreedy算法和KK算法与DCID 算法的运行时间的对比，ICGreedy 算法和KK算法在随着初始节点增加的情况下，运行的时间也随之增大，在初始种子节点个数小于60的情况下，本文算法的运行时间同样地略大于ICGreedy 算法；初始种子节点个数小于50的情况下，本文算法的运行时间也略大于KK算法，但随着初始种子节点个数不断增加，ICGreedy算法和KK算法的运行效率明显低于本文算法。因此，可以看出本文算法在大规模的网络中具有更快的运行效率和更大的传播范围。

6 结束语

在本文中，提出了一种基于节点传播能力的偏向性随机行走的信息传播方法，使用偏向性随机行走参数和节点传播能力参数来进行网络中的信息传播，当传播的关键不再仅限于开始选取的种子节点，而是利用节点本身所能够传播的信息的数量以及随机行走具有的偏向特性，选择网络中的任意一个节点作为信息源的传播节点，结合影响力最大化的传播函数，最终通过选取最优的被传播节点的传播能力C以及偏向性随机行走的参数α来达到网络信息传播范围的最大化，最优参数的获取让本文的算法得到了较好的实验结果。在今后的工作中，将更加着重利用网络的具体特点，选取更符合偏向性随机行走的偏向性参数以及网络中节点能够传播的信息的个数来获取最大的信息传播范围。