雾无线接入网中基于神经网络的资源分配方案

曾舒磊，李学华，潘春雨，王亚飞，赵中原

1.北京信息科技大学 信息与通信工程学院，北京100101

2.北京邮电大学 信息与通信工程学院，北京100876

1 引言

近年来，随着5G 移动通信业务的全面展开，B5G（Beyond 5G，B5G）将进一步扩展支持的通信场景与性能。面对B5G更多样化与更高的性能需求，雾无线接入网正在受到业界的广泛关注[1]。为充分挖掘雾无线接入网的性能潜力，需要对光谱等资源进行适当的管理和分配。资源分配方法，如发射功率控制，波束赋形（Beamforming）设计，边缘缓存控制等，对5G 的推广应用及B5G的进一步演进极为重要。

在传统资源分配方法中，数值优化在解决无线资源管理问题中发挥了重要作用。文献[2]提出一种迭代注水算法；文献[3]采用加权最小均方误差算法（Weighted Minimum Mean Square Error，WMMSE）来设计波束赋形器；文献[4]考虑前传链路（fronthaul）成本，提出一种基于迭代的波束形成设计方案；文献[5-6]考虑联合边缘缓存，提出一种自适应传输选择算法。在此类方案中，算法收敛前必须进行多次迭代，无法适配于实际应用中的实时操作需求。并且，随着用户数量的增加，算法需要更多次数的迭代[7]。

基于深度神经网络的深度学习技术已在许多领域得到应用，如图像分类等，并且已有部分研究证明该方案与传统方案相比性能更优[8-9]。DNN可以通过简单的反向传播算法来解决复杂的非线性问题，而无需推导复杂的数学模型。文献[7]采用深度神经网络来拟合文献[3]中提出的WMMSE 的发射功率控制策略，从而解决了基于WMMSE方案的主要缺点，也就是大量迭代导致的计算时间过长。然而，考虑到这种情况下的主要目标是基于WMMSE 的方案的拟合，基于DNN 方案的可实现容量受限于WMMSE 方案。为突破传统WMMSE方法的性能限制，文献[10]提出基于CNN的功率分配方案。文献[11]考虑全局最优的EE，提出基于DNN 的功率分配方案，文献[12]提出一种基于BP神经网络的移动网络物理层安全方法，然而文献[10-11]所提方案都是基于单对单收发器模型的简单网络，随着5G 移动网络商用，早已无法适配复杂网络及新兴的5G 网络架构所带来的需求与挑战。

为了解决上述算法中暴露出的传统数值优化算法耗时过长、机器学习算法中网络结构无法适配5G 系统等问题，本文提出基于DNN 的F-RAN 资源分配方法。本文的主要贡献概括如下：

（1）运行凸优化迭代算法得到算法输入的波束赋形向量，并提出基于DNN 的F-RAN 资源分配方案。在所提出方案中，通过深度学习技术，以最大化经济频谱效率（ESE）为目标进行自主学习，有效地确定波束赋形方案。本文中的研究是将DNN 应用于F-RAN 中波束赋形设计的初步尝试。

（2）本文创新性地分别使用基于监督学习的归一化均方误差（Normalized Mean Square Error，NMSE）和基于非监督学习的ESE作为损失函数进行训练。

（3）本文在计算机仿真的基础上对所提出方案的性能进行评估。结果表明，相比传统的迭代算法，该方案在实现计算时间大幅度缩短的前提下，SE 和ESE 也能够得到一定的性能增益，此外，本文提出的方案比传统的迭代方案具有更低的时间复杂度。

（4）本文对不同机器学习方案的性能进行评估。结果表明，相比基于监督学习的CNN，本方案的SE和ESE能够得到一定的性能增益。

（5）本文将NMSE和基于非监督学习的ESE作为损失函数应用于CNN，结果表明，本方案与使用相同损失函数的CNN方案具有相似的性能。

2 系统模型

考虑如图1 所示的下行（downlink）F-RAN 场景，该场景包含N个F-AP（Fog Access Point，F-AP）、K个单天线终端（User Equipment，UE）和一个虚拟化基带单元（Building Base band Unite，BBU）池，其中，每个F-AP包含M个天线。所有调度与波束形成都在BBU 池中处理。每个F-AP通过有线或者无线的前传链路连接到BBU池。N个F-AP均匀覆盖在D×D的范围中，并分别使用有线和无线两种典型的前传载波技术[13]，K个单天线终端随机分布在该小区内。将终端与F-AP的集合分别记为K={1,2,…,K}和N={1,2,…,N}，本文假设下行F-AP 通过有线前传链路连接于BBU 池的信道集合为N1={1,2,…,N1}，而通过无线前传链路连接于BBU 池的信道集合记为N2={N1+1,N1+2,…,N} 。假设BBU 池已访问所有终端的数据，并通过前传链路将终端数据分发给F-AP集群。

图1 雾无线接入网架构

将F-APn到终端k的波束形成定义为wkn∈ℂ1×M,终端k的波束形成向量可以表示为wk=[wk1,wk2,…,wkn]∈ℂM×N。则终端k的理论数据速率为：

其中，hk∈ℂM×N为终端k与所有F-AP 天线之间的信道信息（Channel State Information，CSI）矩阵[14-16]，σ2为噪声能量。

模型中F-AP的总容量受到单个链路瓶颈容量的限制[13]，且BBU 池与F-AP 间有线与无线传输方式有不同的限制容量，分别记为R1n(∀n∈N1)与R2n(∀n∈N2)。因此，F-AP需满足的前传链路容量限制可表示为：

频谱效率与能量效率（Energy Efficiency，EE）分别定义为[4，7]：

其中，ak为终端k的权重向量，ξ为功率放大器效率常量，Pc表示F-AP 的静态功率损耗。本文中使用‖ x ‖0表示x 的l0范数，‖ x ‖2表示x 的l2范数，则‖可记为F-APn到终端k的发射功率。

考虑到有线和无线前传链路有不同的成本，将F-APn到BBU 池记为成本系数cn，在此基础上，本文将经济光谱效率定义为[4]：

本文考虑资源分配的经济频谱效率最大化问题，即ESE最大化。为了实现上述目标，须解决以下优化问题：

其中，约束条件C1为F-AP的最大发射功率约束，C2表示BBU池与F-AP间有线传输方式的容量限制，C3表示BBU 池与F-AP 间无线传输方式的容量限制。但是，由于问题（8）的Rk中包含形如等非凸项，为非凸问题，难以直接求得全局最优解。因此，本文采用深度神经网络方法通过数值拟合与优化对问题（8）进行求解。

为方便阅读，本文中使用的仿真参数符号说明表示在表1中。

表1 仿真参数符号说明

3 基于深度神经网络的波束赋形方案

采用传统优化算法（如WMMSE和凸优化迭代算法等）[3-4，17]，时间复杂度高、给系统带来的计算压力大，因此，本文提出使用深度神经网络解决问题（8）中的优化问题。深度神经网络可以针对任意信道条件训练得到一个通用的波束赋形器策略，从而大幅度降低时间成本。在本章中，首先考虑使用DNN 网络拟合文献[4]提出的凸优化迭代算法。这里并不需要对算法每次迭代过程进行拟合。DNN 具备多层隐含层，因此可以以任意精度拟合任意复杂度的函数。

3.1 深度神经网络的结构

这里使用的DNN 结构包含一个输入层、一个输出层和Q个隐藏层，算法结构如图2所示。由于使用多个隐藏层可以显著减少隐藏单元的总数，在保持拟合精度的同时提高计算效率，因此，本文所提的算法中使用多个隐藏层（相比于单隐藏层），同时，将第q个隐藏层记为Dq。在每个隐藏层的输出使用非线性校正函数ReLU（Rectified Linear Unit，ReLU）作为激活层：

这里x,y分别表示ReLU 激活层的输入、输出。此外，为了使DNN 的输出归一化，将输出层的激活函数设为截断的ReLU：

图2 DNN架构

3.2 数据生成

本文中使用的数据按以下方式生成：首先，生成信道矩阵{hk}(i)（遵循第2、4章所提到的信道条件）；然后，运行凸优化迭代算法[4]，导入信道矩阵{hk}(i)，得到算法输出的波束赋形向量{wk}(i)。由于终端的位置和多径衰落不同，因此每个信道样本的信道矩阵和最佳波束赋形向量也不一样。

为方便神经网络计算，将信道矩阵hk进行标准化（normalization），将表示为标准化输出，则有=同时，将波束赋形向量wk进行归一化，将表示为归一化输出，即：

3.3 训练

准备好训练样本后，使用NMSE作为损失函数进行训练。将神经网络的输出记为yk，此时损失函数为：

因此，拟合训练后的结果是凸优化迭代方案的近似值。随后，神经网络可以使用优化目标作为损失函数做进一步训练。把最大化ESE 作为优化目标时，损失函数为：

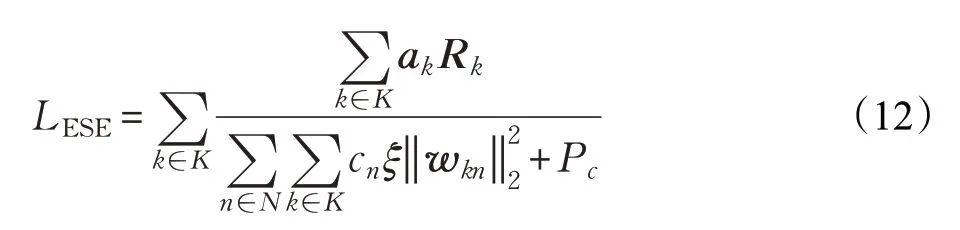
值得注意的是，使用ESE 作为损失函数训练时，没有监督项，此时的神经网络是非监督学习。

本论文使用的优化算法为RMSProp。其中，衰变率为0.9，通过交叉验证选择合适的batch 大小和学习率。DNN 模型是按照顺序分别使用Lfit和LESE进行训练的，这样DNN模型首先使用Lfit进行训练，并且在训练后使用LESE进行训练。为了进一步提高训练性能，首先使用截断正态分布初始化权值，然后将每个神经元的权值除以其输入个数的平方根，使每个神经元输出的方差归一化。

3.4 测试

根据当前的信道条件，采用训练后的DNN 来确定波束形成向量，将DNN的输出记为{ yk}(i)。用作标签的数据是被做归一化处理后的数据，因此，要将输出的{ yk}(i)进行还原，将还原后的数据记为，则

图3 输出算法流程图

经过处理后的数据虽然无法保证训练对所考虑的优化问题的最优解的收敛性，但与传统的优化方案相比，此处提出的优化方案在F-AP的最大发射功率值Pmax较大可以获得更好的解，仿真结果可以证实这一点。

图4 CNN结构

3.5 基于CNN的波束赋形方案

CNN 算法同样可用于解决式（8）中提出的优化问题，从而根据信道条件决定波束赋形。

这里使用的CNN 结构包含一个卷积部分，一个全连接层（Fully Connected，FC）和一个激活层（Activation Function），详情可见图4。

卷积部分由串联的Nc子块组成，每个子块包含一个卷积层和一个ReLU层。卷积核（filter）的大小设置为2×2，步长（stride）设置为1，并使用0填充，以便输出的大小与输入的大小保持一致。第i个子块的卷积核数量设置为Ci。每个卷积层的输出被送入ReLU层，以防止负值。

在FC 层，卷积部分的输出被合并减少至K×N×M，用于确定波束赋形。随后，将FC层的输出导入激活层，这里使用截断的非线性函数ReLU（10）作为激活函数，使CNN的输出归一化。

与DNN相似，这里将标准化信道矩阵hk作为CNN的输入，将CNN 输出记为yCk。首先使用NMSE 作为CNN的损失函数进行训练：

CNN训练将使用与DNN相同的优化方法和权重初始化方法，并在随后的仿真结果中分别展示损失函数为L(C)fit与L(C)ESE时的算法性能。

4 实验结果与分析

本章比较了深度神经网络与凸优化迭代算法、WMMSE 方法等方案的性能。在仿真中，考虑一个F-RAN 小区，F-AP 数量N=3，小区范围D=0.5 km 。这里需要指出的是，更多的F-AP 只将带来更高的计算复杂度，而所提出的解决方案仍然可以在保持类似的性能趋势下工作。在三个F-APs中，假设其中一个通过无线前传链路连接至BBU 池，另外两个使用有线前传链路。每个F-AP天线数M=2。假设该F-RAN小区包含的 终 端 数 为K=9 ，噪 声 功 率 谱 密 度σ2=-174 dBm/Hz[18]。从F-AP 到终端的路径损耗指数为4，衰弱系数为单位方差的同分布瑞利随机变量（Rayleigh random variables）。假设所有F-AP具有相同的最大发射功率，即max,∀n。对于前传连接，有线与无线前传连接容量约束值分别为10(bit ⋅s-1)/Hz与5(bit ⋅s-1)/Hz 。F-AP 的静态能量损耗Pc=30 dBm，功率放大器的功率效率为ξ=2。由于有线前传传输比无线前传传输带来更高的开销，因此前传链路成本系数被设置为满足cwl＜cw＜1，在本文中，cw=0.5 ，cwl=0.25。

为考虑计算机效率，神经元数量最好为输入的2n倍[19]，因此，在本文所用的DNN 中，隐藏层数量Q=3，D1=216，D2=432，D3=432。此外，为训练（训练集，training dataset）和验证（验证集，validation dataset）分别生成20 000 个通道样本，初始学习率设置为0.000 1，训练batch 大小设置为50。另外，在本文所用的CNN中，卷积层数量Nc=7，卷积核数量Ci=8。

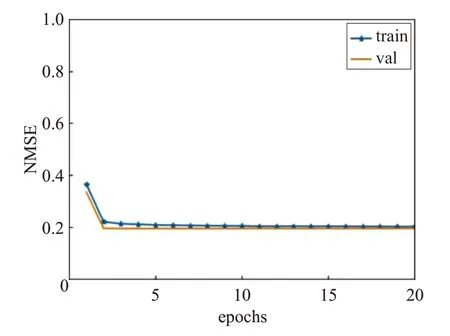
图5 训练集和验证集的损失率变化

4.1 拟合性能

图5 展示了损失函数为Lfit时DNN 的性能。用Ltrain与Lval分别表示Pmax=15 dBm 时训练集和验证集随着训练循环次数（epoch）的增加所对应的Lfit值。可以观察到，Ltrain与Lval很快接近于0.2。此外，随着训练循环次数（epoch）继续增加，Ltrain与Lval都没有增加，从而可以得出结论，即训练程序可以很好地适应训练集，而不存在过拟合（overfitting）或者欠拟合（underfitting）的情况。

4.2 SE与ESE性能

考虑优化目标为最大化ESE的神经网络，在图6中表示为DNN，并分别与WMMSE方案、凸优化迭代方案和两种CNN方案进行比较。图中CNN（fit）表示损失函数为L(C)fit时的SE 和ESE 性能，CNN（ESE）表示损失函数为L(C)ESE时的SE和ESE性能。

图6（a）和（b）分别展示了不同F-AP 最大发射功率下五种算法的SE 与ESE 性能。可以看出，使用LESE作为损失函数下的DNN 网络都能获得接近于或者超出凸优化迭代算法的性能；损失函数为L(C)fit时，CNN性能差于DNN 和凸优化迭代算法，而损失函数为L(C)ESE时，CNN 性能与DNN 相似。需要指出的是，在实际仿真过程中，由于有时间复杂度限制，凸优化迭代算法会设置有限的迭代次数上限与一定的迭代精度，并且将非凸问题变换为迭代的凸问题求解，使得凸优化迭代算法只能求得局部解，而本文采用的神经网络拟合方法在F-AP 最大发射功率Pmax较大时性能可以超出凸优化迭代算法，在Pmax=20 dBm 点时ESE 的增益为20%。

图6（a）不同前传链路设置下SE对比

图6（b）不同前传链路设置下ESE对比

4.3 时间复杂度

图7 表明了不同终端数量下各种算法所需的计算时间。从图中可以看出，DNN 的计算时间要远远短于WMMSE 方法与凸优化迭代算法，并且DNN 的计算时间与WMMSE、凸优化迭代算法的计算时间之间的差距随着终端数量的增加而增大，而CNN 的计算时间与DNN相似。

图7 不同算法计算时间对比

5 结论

本文提出了基于神经网络的优化方案，主要解决F-RAN下的ESE性能优化问题。通过训练，本文提出的神经网络方案能够自主学习任意信道条件下的资源分配策略，训练后的神经网络相比传统采用凸优化的迭代方案来说，具备更小的时间复杂度。为验证算法性能本文还提出一种具备相同损失函数的基于CNN的优化方案。仿真结果表明，神经网络与传统的凸优化方案具有更好的ESE 性能，并且，本文提出的算法具备更低的时间复杂度，与此同时，使用相同损失函数的CNN方案具备与DNN相似的性能与时间复杂度。