可实现时分复用的CNN卷积层和池化层IP核设计

张 卫，刘宇红，张荣芬

贵州大学 大数据与信息工程学院，贵阳550025

1 引言

当前，深度学习（Deep Learning）得到了广泛的应用与发展[1-2]，而CNN也在越来越多的场景中被使用，诸如在视频分析[3-4]、人脸识别[5-6]等领域都得到了广泛的应用，尤其是在图像识别场景中取得了突破性的进展。

CNN 是一种拥有多层感知器、局部连接和权值共享的网络结构[7]，有较强的容错、学习和并行处理能力[8]，从而降低了网络模型的复杂性和网络连接权值的个数。虽然CNN 的应用广泛，但需要大量时间来训练其模型的参数，特别是在参数数据量很大时。现阶段实现CNN主要采用消费级的通用处理器（Central Processing Unit，CPU）来实现[9]，数据量过大时会采用图形处理器（Graphics Processing Unit，GPU）来实现。近年来，基于FPGA 实现的方式凸显出巨大的优势[10]。CNN 是典型的并行运算模型，在CNN的卷积层和池化层中，每一层的卷积运算都只与当前层的特征运算核相关，与其他层相比具有独立性和不相关性。而FPGA 作为一种高度密集型计算加速器件，其硬件结构有助于算法中并行运算的加速[11]。当前，利用FPGA 实现CNN 的方式以Verilog HDL 和HLS 为主。北京大学软件与微电子学院采用Verilog HDL语言来设计IP核[12]，并根据CNN模型设置了多种不同种类的IP 核，可实例化不同的CNN网络，充分利用FPGA 的并行性提升了CNN 运算速度和效率，但IP核设计过于复杂，通用性不强，并且需要具备一定的硬件逻辑知识才能使用这些IP核。而HLS实际上是把高层的C、C++或SystemC的代码综合成Verilog HDL 描述，具有易于理解与使用、开发时间短等特点，故本文采用HLS来设计CNN中的卷积层和池化层的IP核，进而利用IP核来搭建整个系统。

本文首先对深度学习中的CNN算法模型及结构进行介绍和研究，然后将CNN 模型中的卷积层和池化层设计为IP 核，通过将函数的运算规模参数协议设为axi_master，减少了模型分类的时间，提升了模型运算性能。为了验证IP核的功能性，本文进一步采用时分复用技术在FPGA平台上对MNIST数据集进行了系统验证。

2 CNN算法模型

2.1 CNN模型

神经网络是一种模仿生物的神经网络结构和功能的数学模型，可以模拟人的判断能力。CNN 是神经网络的一种，在图像和语音识别方面能够给出更好的判断结果。

CNN 包含卷积层、池化层和全连接层。典型的卷积神经网络结构如图1所示。一个卷积块为连续M个卷积层和个b池化层，一个卷积网络可以堆叠N个连续的卷积块，然后再接着K个全连接层。其中，卷积层通过“卷积核”作为中介。同一个卷积核在所有图像内是共享的，图像通过卷积操作后仍然保留原先的位置关系，能得到图像中的某些特征。但通过卷积层处理的特征维度大，数据量大，需要使用池化层进行下采样后才可进行分类。池化层保留数据中最显著的特征，不会对数据丢失产生影响。全连接层则是一个完全连接的神经网络，根据权重每个神经元反馈的比重不一样，最后通过Softmax函数得到分类的结果。

图1 典型的卷积网络神经结构

得到分类结果后，CNN 通过误差反向传播算法来进行权重参数和偏置参数的学习，这主要通过计算卷积层中参数的梯度来实现。具体计算过程可由如下公式表示。

第l个卷积层的第p(1 ≤p≤P)个特征映射净输入Z(l,p)可由公式（1）表示：

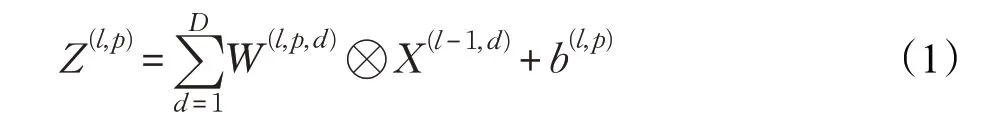
其中，X(l-1)∈R(M×N×D)为第l-1 层的输入特征映射，W(l,p,d)和b(l,p)为第l层的卷积核以及偏置，该层共有P×D个卷积核和P个偏置，可以分别使用链式法则来计算其梯度。

损失函数L(Y,Ŷ)关于卷积核W(l,p,d)和偏置b(l,p)的偏导分别由公式（2）和公式（3）表示：

其中，1 ≤i≤M-l+1,1 ≤j≤N-p+1。可以看出，每层参数的梯度依赖其所在层的误差项δ(l,p)。卷积层和池化层的误差项的计算不同，分别由公式（4）和公式（5）表示：

2.2 本文CNN模型

本文所设计的CNN 模型结构如图2 所示。该结构有10 层，第1 层和最后一层分别是输入层和输出层，输入层完成测试图像数据的输入获取，因为实验中采用MNIST数据集，所以输入数据为784个。输出层与前一层连接的权重个数为20×10=200，输出结果为10种。为了降低过拟合，系统在输出层的前一层还加入了Dropout层。

第1、2、3、4、6、8 层为卷积层，卷积核有5×5 和3×3两种，卷积核移动步长均为1，无填充。第5层和第7层为池化层，池化步长均为2，均采用最大池化。系统设计采用Relu函数作为激活函数。

各卷积层的参数为：

卷积层1 权重为5×5×5=125个，偏置为5个。

卷积层2 权重为5×5×5×5=625个，偏置为5个。

卷积层3 权重为3×3×5×5=225个，偏置为5个。

图2 本文设计的CNN网络层次结构图

卷积层4 权重为3×3×5×5=225个，偏置为5个。

卷积层6 权重为3×3×5×10=450个，偏置为10个。

卷积层8 权重为3×3×10×20=1 800个，偏置为20个。

因此整个卷积层总共有3 270个参数。

3 CNN模型中的卷积层IP核和池化层IP核的设计

图2 模型中卷积层和池化层均采用HLS 来实现。HLS 实际上是把高层的C、C++或SystemC 的代码综合成Verilog HDL描述，然后用下层的逻辑综合来获得网络表，最后生成硬件电路。本文采用C 语言来编写代码，使用Vivado HLS工具来生成IP核。

3.1 卷积层IP核

编写C 语言后，添加人为约束，就可以得到想要的硬件电路。其中，人为约束是设计电路的重点。本文设计的卷积电路是通用的，支持不同规格的输入。用于实现卷积层IP核的Conv函数的表达式如下所示：

void Conv（）

{填充运算

for循环1：遍历CHout

for循环2：遍历Hin

for循环3：遍历Win

{for循环4：遍历Ky

for循环5：遍历Kx

{for循环6：遍历CHin

{tp=feature_in[h*CHin*Win+w*CHin+cin]*

W[ii*Kx*CHin*CHout+jj*CHin*CHout+cin*CHout+cout]；

sum+=tp；}}

sum+=bias[cout]；

feature_out[i*Wout*CHout+j*CHout+cout]=sum；}}

式中，CHin、Hin、Win分别为输入特征的通道数、高、宽，CHout为输出通道，Kx、Ky为卷积核的大小，Sx、Sy为步幅大小，mode是卷积的填充模式，relu_en是relu函数的使能，feature_in[]、feature_out[]、W[]、bias[]是输入、输出特征的运算规模大小。

从Conv 函数的表达式可以看出，tp为输入特征feature_in[h][w][cin] 和权重w[ii][jj][cin][cout] 进行卷积运算的结果，再加上偏置值bias[cout]，即可得到输出特征的值feature_out。对于有不同的高、宽、通道的图像输入、不同大小的卷积核滤波器，均可以使用该函数。通过Export RTL 操作，Conv 函数可生成如图3（a）所示的IP 核，该IP 核的性能指标Latency 和Interval 如图3（b）所示。

图3 卷积层IP核及其性能指标

卷积运算通过6 个for 循环遍历输入输出来实现，基本思想是采用滑窗法，而对其中的参数的优化更为重要。对于函数中的运算规模参数，本文采用s_axilite 协议进行约束优化，可生成s_axi_AXILiteS 接口，用于更快地配置电路。对于函数中的数据来源参数，采用m_axi 协议进行约束优化，可生成m_axi_gmen 接口，这便于卷积层主动从存储器中读取特征数据和写入运算结果，其工作过程如图4所示。这里因为参数可配置导致for循环的边界为变量，所以无法使用pipiline来并行化流水线进行加速，会在一定程度上限制卷积运算的速度。

图4 卷积层IP核在系统中的工作过程

3.2 池化层IP核

池化层的设计原理与卷积层类似。通过Pool 函数生成的池化层IP 核也可对不同规模的输入做池化运算。池化运算通过5 个for 循环来实现，并可选择性地做平均池化、最小池化和最大池化。通过Export RTL操作生成的池化层IP 核如图5（a）所示，该IP 核的性能指标Latency 和Interval 如图5（b）所示。Pool 函数的表达式如下所示：

void Pool（）

{for循环1：遍历CHin

for循环2：遍历Hin/Ky

for循环3：遍历Win/Kx

{for循环4：遍历Ky

for循环5：遍历Kx

判断池化模式：

平均池化：

sum+=（feature_in[h*CHin*Win+w*CHin+c）]/（Kx*Ky）；

最小池化：

sum=min（sum，feature_in[h*CHin*Win+w*CHin+c]）；

最大池化：

sum=max（sum，feature_in[h*CHin*Win+w*CHin+c]；}

feature_out[i*Wout*CHin+j*CHin+c]=sum；}

式中，CHin、Hin、Win分别为输入特征的通道数、高、宽，Kx、Ky为卷积核的大小，mode 是池化的模式，feature_in[]、feature_out[]为运算规模大小。

图5 池化层IP核及其性能参数

图6 给出了池化层IP 核在系统中的工作过程。池化层IP 核接收到CPU 发来的指令后，主动从存储器中读取特征数据，池化运算完成后，将运算结果写入存储器中。

图6 池化层IP核在系统中的工作过程

4 CNN系统实现

4.1 硬件实现

系统的硬件部分包括ZYNQ处理器、两个卷积层IP核、一个池化层IP 核以及连接各部分的axi总线。接收到ZYNQ处理器发来的指令后，IP核自行从存储器中获取神经网络的权重参数、偏置参数[13]以及图像数据，并将神经网络算法分类的结果写入存储器中。使用vivido工具完成的系统硬件图如图7所示，两个卷积层IP核的m_axi_gmen 均连至ZYNQ 处理器的S_AXI_HP0 接口，池化层IP 核的m_axi_gmen 连至S_AXI_HP1 接口，ZYNQ 处理器的M_AXI_GP0 口同时连接三个IP 核的s_axi_AXILiteS接口。

4.2 软件实现

硬件完成后，先生成比特流文件，再使用SDK工具开始软件设计。软件设计主要是搭建CNN 的网络结构，并将其中的卷积层和池化层运算通过调用RunConv和RunPool 函数来实现。RunConv 函数中的InstancePtr参数为卷积层IP核的指针，通过这个指针可以调用不同的卷积层IP 核，当指针指向0 时调用Conv_0 IP 核，指针指向1 时调用Conv_1 IP 核。RunPool 函数中也定义了类似的指针，本文网络中池化电路需求较少，且为了节约资源，本文只定义了一份池化电路，故指针一直指向0，调用Pool_0 IP 核。实际上，Conv_0 IP 核硬件电路用于计算核为5×5 的卷积运算，Conv_1 IP 核用于计算核为3×3 的卷积运算，Pool_0 IP 核硬件电路用于计算最大池化。

利用时分复用技术，可加速整个系统的运算。图8详细阐述了文中时分复用技术的应用。在一张图片的测试过程中，将图片数据输入神经网络后，卷积层C1和C2通过Conv_0 IP核进行计算，卷积层C3、C4、C6和C8通过Conv_1 IP 核进行计算，池化层P5 和P7 均通过Pool_0 IP核进行计算。根据FPGA的并行性[14]，三个IP核硬件电路同时运行，能提升整个CNN 网络的运算性能。

图7 系统硬件图

图8 时分复用技术应用图

5 系统仿真与分析

系统设计中的具体硬件使用Xilinx 公司的ZYNQ-7000 xc7z010clg400-1 芯片作为试验平台，该芯片内部拥有28 KB个逻辑单元，2.1 MB的嵌入式存储器，80个嵌入式乘法器，片内资源较为丰富，基本能够满足该网络模型中硬件设计所需要的资源。CPU 软件训练平台使用Core i7-8700k处理器，主频为3.4 GHz。

该硬件部分的系统资源消耗如表1 所示。系统设计中采用了大量的if语句和for循环语句用来进行卷积运算和池化运算，导致系统中LUT 和FF 以及DSP 的逻辑资源消耗较多，但可以看出本文所使用的ZYNQ器件基本能够满足硬件框架需求。

表1 硬件部分的资源消耗

训练过程中，以学习率为0.5、每次输入批次为50、迭代次数为10 000 在CPU 中进行训练[15]，训练集为MNIST数据集中的60 000张像素为28×28的灰度图片，图像数值范围为0～255，最终对MNIST数据集的10 000张手写数字测试图片进行测试得到的平均识别正确率为96.83%。

测试过程中，先将CPU 中已训练好的网络算法的权值参数、偏置参数以及MNIST 数据集的10 000 张手写数字测试图片存储在SD 卡中，PS 端给出指令后，IP核读取SD 卡内数据，运算完成后再将分类结果存储在存储器中，最后通过串口打印出分类结果。某次测试中串口打印的部分结果如图9所示，其中，第925张图片的预测值为0，实际的数字为2，预测错误，其余图片均预测正确。如表2 所示，经10 000 次迭代测试后，各手写数字的整体识别正确率为95.34%，与软件平台正确率96.83%基本一致。表3 给出了各手写数字的识别正确率，其中手写数字6的正确率最差，为91.57%，但仍在可接受范围内。

FPGA 硬件平台和CPU 软件平台所需的测试用时如表4所示，神经网络在CPU软件平台上迭代1次需要5.633×10-2s，而在FPGA 硬件平台上[16]迭代1 次需要1.941×10-2s，再结合10 000次迭代后的测试用时对比，可以看出采用多个卷积层IP核实现时分复用后对电路的加速效果约为3 倍。但因为实现卷积层和池化层IP的函数参数可配置，导致不能对函数内for 循环做并行优化和流水优化，故算法的加速效果受到一定限制。

图9 串口打印的部分结果

表2 FPGA硬件平台和CPU软件平台的整体识别正确率对比

表3 各手写数字的识别正确率

表4 FPGA硬件平台和CPU软件平台所需的测试用时对比

值得一提的是，由于FPGA与GPU并行处理的机理类同，若采用GPU服务器开展对比，根据文献[17-19]可知，本文最终的识别效果和加速性能与GPU 模式的性能大抵相当，其优势在于基于FPGA 的CNN 系统可以部分替代GPU 服务器开展相应的图片处理工作，在嵌入式应用、边缘计算方面具有更好的应用前景。

6 结束语

本文通过使用HLS 设计了一种可实现卷积运算和池化运算、可配置参数的IP核，并利用时分复用技术和生成的IP 核在FPGA 平台上实现了整个10 层网络的CNN系统算法结构。针对MNIST数据集的实验结果表明，该硬件系统的10 000次迭代的准确率为95.34%，与CPU软件平台准确率基本一致。不足的是，由于实现IP核的Conv 函数和Pool 函数的参数均为变量，无法使用pipeline和流水线技术对函数中的for循环进行加速，导致系统的加速性能受限。但利用时分复用技术使得多个IP 核同时参与运算，最终的加速性能约为CPU 系统的3 倍，能够与GPU 的加速性能大抵相当，在嵌入式应用、边缘计算方面，具有潜在的应用前景。总的来说，利用本文设计的IP核，可以使用FPGA在短时间内实现一个CNN硬件系统，并能部分替代GPU工作，充分体现了HLS的快捷性，对指导基于Verilog HDL的CNN硬件实现也具有重要意义。