基于特征分析的目标仿真模型相似度评估方法研究
2020-12-26张小威王丙乾
李 凡,张小威,王丙乾,耿 旭,李 奇
(上海机电工程研究所,上海 201109)
0 引 言
目标仿真模型相似度评估是在建模与仿真应用目的下确定仿真结果能否准确代表实际系统的过程,是确保建模与仿真可信性的重要途径。目标仿真模型是对真实目标特性的一种近似模拟,通过外场实测数据与内场测试数据的对比分析,可以对内场目标仿真模型的可信度进行评价,分析内场目标仿真模型与外场实际目标的相似度或一致性。国内从80年代开始,对仿真可信性开展了研究,主要围绕校核、验证与验收(verification, validation and accreditation, VV&A)的理论和方法,并对这些方法开展了应用[1-3]。目标仿真模型相似度评估正是利用了VV&A的理论和方法,通过模型校核和验证,使仿真系统能够在一定程度上复现原型系统的行为,从而达到特定的仿真目的。
针对特定的仿真目的,在相同的试验框架下,必须证实模型行为特性与系统行为特性的相似程度是否满足要求。因此,必须开展目标仿真模型相似度分析,从而确保半实物仿真试验结果的置信度。国内在目标红外辐射特性仿真方面尚未建立起一套统一的评估准则来对各种目标的红外仿真模型本身进行评估。目标与环境光学特征国防科技重点实验室的毛宏霞等[4]初步研究了对目标红外特性模型的评估方法;空军工程大学田晓飞[5]等设计了将起始时刻等效逼真和变化过程逼真相结合以评估整个红外目标模拟逼真度的方案,具有一定意义。
本文主要针对红外成像探测器,通过对目标仿真模型的特征分析,建立了目标仿真模型的相似度评估模型,探讨了一种基于特征分析的相似度评估方法。利用实际的飞行数据与半实物仿真数据进行对比,对目标仿真模型可信度进行评估,算例结果表明基于特征分析的相似度评估方法具有一定的实用价值,此方法为同类型的仿真模型相似度评价提供了很好的借鉴价值。
1 目标仿真模型的特征分析
在半实物仿真中,目标按照“相对等效”原理进行模拟。这种等效并不是指模拟的目标直接相似于真实的目标,而是模拟目标信息投射到成像探测器上产生的各种响应逼真于实战应用中成像探测器上产生的各种响应,称为等效逼真。因此,要分析目标模拟场景逼真于实战设置场景的误差程度,必须以成像探测器上采集到的信号信息为依据。成像探测器采集到的信号信息可分为静态信息和动态信息,其中静态信息主要指单帧图像包含的信息,动态信息主要指按仿真时间推进的图像序列包含的信息。
1.1 静态信息
为了评价两幅图像的相似程度,可以通过分析成像探测器所敏感的特征信息,综合这些特征信息,建立相应的评价指标,最终完成静态信息的相似度评价。成像探测器在目标检测、识别与跟踪过程中,所敏感的图像特征信息包含峰值信噪比、图像结构信息(含图像对比度、图像亮度和图像结构)以及图像梯度信息等。
1) 峰值信噪比
峰值信噪比(peak signal-to-noise ratio,PSNR)作为目标检测中的重要指标,基于通信理论而提出,是最大信号量与噪声强度的比值。由于数字图像都是以离散的数字表示图像的像素,因此采用图像的最大像素值来代替最大信号量。PSNR的表达式为
(1)
式中,M、N分别表示图像的长和宽;MSE(mean square error)为图像的均方误差,可以表示为
(2)
式中,f(i,j)为真实图像;f′(i,j)为仿真图像(i=1,2,…,N,j=1,2,…,M)。PSNR值越大,说明两幅图像相似度越高。
2) 图像结构相似度
探测器的主要功能是提取图像中的结构信息,而且能高度自适应地实现这一目标,因此对图像结构失真的度量才是对图像感知质量的最好近似。在此基础上,提出了一种基于图像结构的全参考图像质量评价方法,即结构相似度(structural similarity,SSIM)[6]。测量结构信息的改变可以得到图像失真的近似值。该算法首先计算两幅图像的亮度比较函数l(x,y)、对比度比较函数c(x,y)以及结构比较函数s(x,y).然后将3部分函数利用指数函数进行合并,最后得到一个全局相似性测量的结构相似度,具体过程如图 1所示。
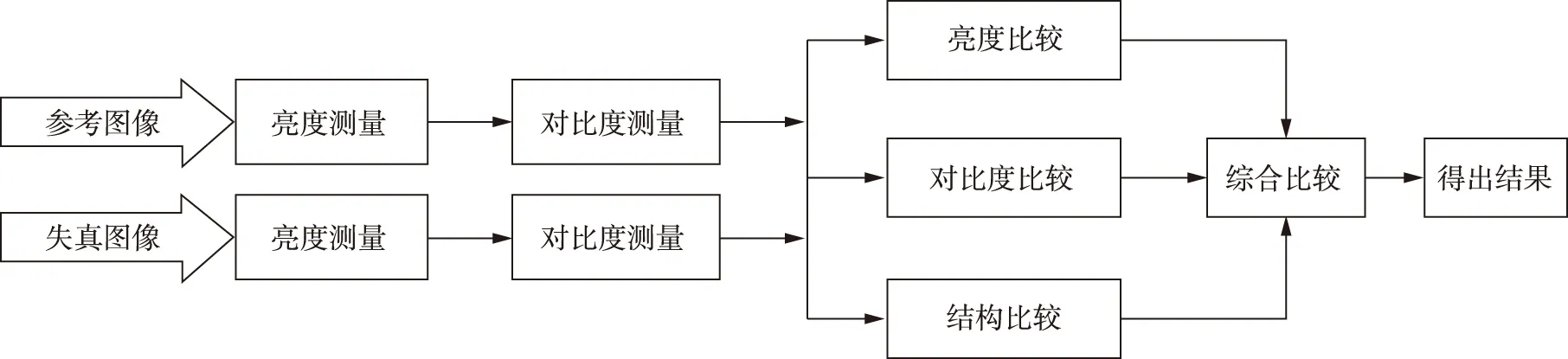
图1 结构相似度计算过程Fig.1 Process of SSIM calculation
假设x,y分别代表原参考图像和待测图像,x={xi|1,2,…,N},y={yi|1,2,…,N}。亮度采用均值(μx,μy)得到,对比度采用标准差(σx,σy)得到,结构相似度采用协方差σxy得到。则亮度对比函数、对比度比较函数、结构比较函数分别表示为
(3)
式中:
由此可得
SSIM(x,y)=[l(x,y)]α·[c(x,y)]β·[s(x,y)]γ
(5)
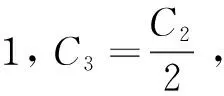
(6)
式中:C1=(K1L)2;C2=(K2L)2;L表示图像像素点的动态范围;K1、K2是两个很小的常数。图像结构相似度的值越大,说明两幅图像的结构相似度越高。
3) 图像梯度
梯度可以很好地反映图像中微小细节的反差和纹理变化,可以用来评价图像的清晰程度,所以将梯度作为图像的主要结构信息,进而提出了基于梯度的结构失真的图像质量评价方法。
对于数字图像一般用差分运算代替微分运算,梯度可用差分公式来近似,采用4邻域绝对值之和表征图像梯度幅度值,设原始图像为x,像素坐标为(i,j),则在坐标(i,j)上的梯度Gx(i,j)的表达式为
Gx(i,j)=|x(i,j)-x(i-1,j)|+|x(i,j)-x(i,j-1)|+
|x(i,j)-x(i+1,j)|+|x(i,j)-x(i,j+1)|
(7)
则图像x与y的梯度相似度(gradient similarity, GSIM)为
(8)
式中,Gx(i,j)、Gy(i,j)分别为图像x与图像y在(i,j)点处的梯度幅度值。梯度相似度的值越大,说明两幅图像的相似度程度越高。
1.2 动态信息
在半实物仿真过程中,成像探测器所敏感到的目标特征动态信息,主要体现在按仿真时间推进时目标的能量信息和目标的面积信息,成像探测器以此为依据对目标进行识别和跟踪。
1) 能量信息相似度
成像探测器通过半实物仿真系统采集到场景信息后,通过图像预处理算法、信号处理算法后,可以获得弹道信息中的目标/干扰/背景能量信息随时间变化的曲线。通过半实物仿真采集到的能量信息随时间变化的曲线与靶试数据中获得的能量信息随时间变化的曲线进行对比,相似度函数ρ(·)如式(9)所示。
(9)
式中:xi|i=1,2,…,N为真实系统输出的时间序列曲线;yi|i=1,2,…,N为仿真系统输出的时间序列曲线。利用式(9)计算得到能量信息相似度ρE(·)。
2) 面积信息误差
成像探测器通过半实物仿真系统采集到场景信息后,通过图像预处理算法、信号处理算法后,可以获得弹道信息中的目标/干扰/背景所占成像像面的面积信息随时间变化的曲线。通过半实物仿真采集到的面积信息随时间变化的曲线与靶试数据中获得的面积信息随时间变化的曲线进行对比,利用式(9)所示的相似度函数ρ(·),计算得到面积信息相似度ρS(·)。
2 基于特征分析的相似度评估方法
2.1 相似度评估指标
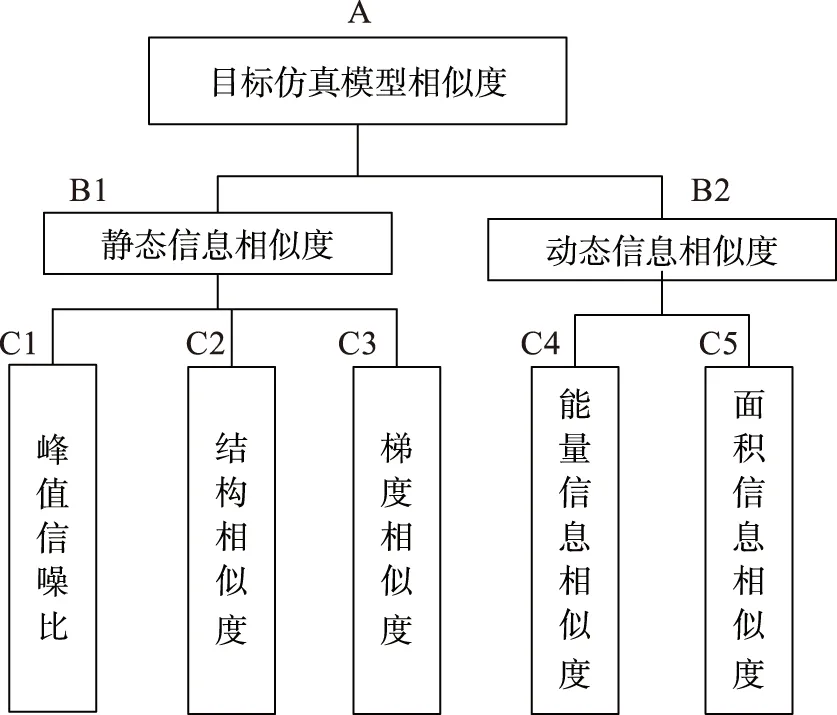
图2 相似度评估指标示意图Fig.2 Similarity evaluation indexes
基于上述分析,构建基于特征分析的目标仿真模型相似度评估指标,如图 2所示。其中,峰值信噪比C1、结构相似度C2、梯度相似度C3、能量信息相似度C4和面积信息相似度C5为底层指标,静态信息相似度B1和动态信息相似度B2为中间层指标,光电信号仿真误差A为顶层指标。
2.2 权重设计
权重是以某种数量形式对比、衡量被评估对象总体中诸要素相对重要程度的量值,也就是各指标对总体目标的贡献大小。指标权重直接影响着误差分析的结果,本文采用AHP[7]计算权重,通过两两比较因素(目标、准则或方案)的相对重要性,给出相应的比例标度;构造上层某要素对下层相关元素的判断矩阵,然后得出相关元素对上层某要素的相对重要性序列;最后综合决策者的判断,确定被选方案相对重要性的总排序。
采用AHP进行权重确定的基本步骤是构造判断矩阵、计算权重、一致性检验。
1) 构造判断矩阵
基于指标体系结构,构造每一子层的判断矩阵,该子层某两个元素相对于上一层某元素的重要性比值便构成该层判断矩阵的各元素,判断矩阵赋值采用10/10-18/2的标度[8]代表元素不同的重要程度,具体描述见表1。

表1 10/10-18/2尺度含义Tab.1 Scale of 10/10-18/2
构建判断矩阵A=(aij)n×n,aij为根据表 1得到的标度量化值。
选择适当的标度方法将判断矩阵定量化后应当满足完全一致性条件如下:
① 判断矩阵A对角线元素应当为1;
② 判断矩阵A的左下三角和右上三角各对应元素应当互为倒数;
2) 计算相对权重
根据某一层次上的某些因素对上一层因素的判断矩阵,计算出该判断矩阵的最大特征值及其所对应的特征向量,所求特征向量也就是各评价因素的重要程度,将其归一化后即为权数向量。
将判断矩阵A=(aij)n×n按列归一化,即
(10)
按行加总,得
(11)
再归一化后即得权重系数

(12)
最大特征根为
(13)
式中,n为判断矩阵的阶次;(Aw)i代表向量AW的第i个元素,W=(ωi)n×1。
3) 一致性检验
建立判断矩阵后还需对其进行一致性检验,以确定人们的判断是否一致。
这里用随机一致性比率(consistent ratio,CR)来检验判断矩阵是否具有满意的一致性,若CR<0.10,判断矩阵具有满意的一致性;否则不满足一致性检验。
随机一致性比率CR是用判断矩阵的一致性指标(consistency index,CI)与同阶次的平均随机一致性指标(random index,RI)之比来定义的,即CR=CI/RI。其中,随机一致性指标RI随判断矩阵阶数n的改变而改变,如表 2所示。判断矩阵的一致性指标CI=(λmax-n)/(n-1),CI越大,判断矩阵的不一致性越严重。

表2 平均随机一致性指标Tab.2 Index of average random consistency
若判断矩阵没有通过一致性检验,那么就需要对矩阵中各元素进行修正重新赋值,即:
1) 将判断矩阵中第n列元素系数归1;
2) 观察判断矩阵各纵列元素大小是否相近,若某列中某些数据与其他数据相差较大,则可以从物理意义上对这些元素进行适当修正;
3) 若判断矩阵各列在同一行上出现偏大或偏小的现象,则可以修正该行在最后一列元素的赋值。
2.3 上层指标综合
根据归一化指标向量以及计算得到的权重向量进行综合评价。此处使用加权平均的方法来计算综合误差,即
(14)
式中:C(S)表示综合误差结果;C(Si)表示各指标误差结果;wi表示权重因子;i为指标数量。
3 算例分析
将通过成像探测器采集到同一条弹道相同时刻半实物仿真的图像信息和实际飞行过程中采集到的图像信息进行对比分析,如图3所示。通过采样两条弹道中相同时刻的图像信息进行对比,取指标均值即可获得该指标的计算数值。

(a) 仿真图像

(b)实测图像
将能量曲线的半实物仿真数据和实测数据绘制在一个时域图中,如图4所示。
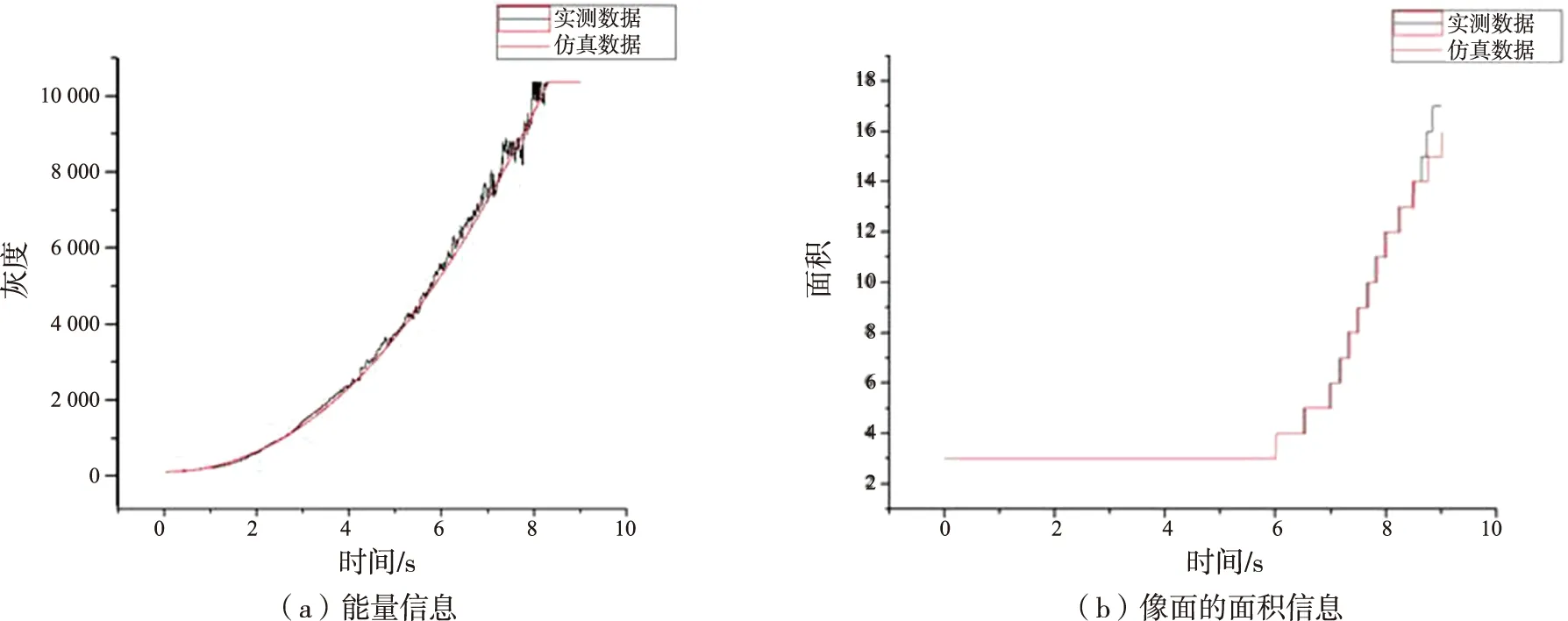
图4 动态信息曲线对比Fig.4 Comparison of dynamic information
根据上述半实物仿真实测数据和第1章中各指标的计算公式,可得到峰值相似度为85.3%,结构相似度为96.1%,梯度相似度为28.2%,能量信息相似度为78.3%,面积信息相似度为88.5%。
根据AHP计算权重值,静态误差所包含的下层指标为C1、C2和C3,动态误差所包含下层指标为C4和C5,根据指标相对上层指标的相对重要性,可以得到在静态误差中4个指标相对上层指标的相对重要程度为峰值信噪比>结构相似度>梯度相似度,能量信息相似度>面积信息相似度。
建立三角形调查表记录专家打分结果,由于每一比较判断栏中左边的因素比右边的因素重要,只需将其判断的重要性程度对应的数字记号填入中间的判断框即可。总体判断由左向右逐列进行,且在判断中始终保持“右边判断栏中的重要程度数字记号应比由‘>’线连接的左边任何一个判断栏中的重要程度数字记号都大”这一逻辑关系。本文选择10位专家根据表 1标度表示法进行三角形调查表的填写,他们的判断结果如图 5所示。
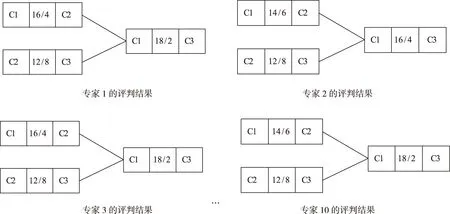
图5 三角形调查表结果图Fig.5 Results of triangle questionnaire
因此,根据各位专家的评判结果,依据少数服从多数的原则,选取专家1、3、4、7、8、9的评判结果,得到的判断矩阵如表 3和表 4所示。
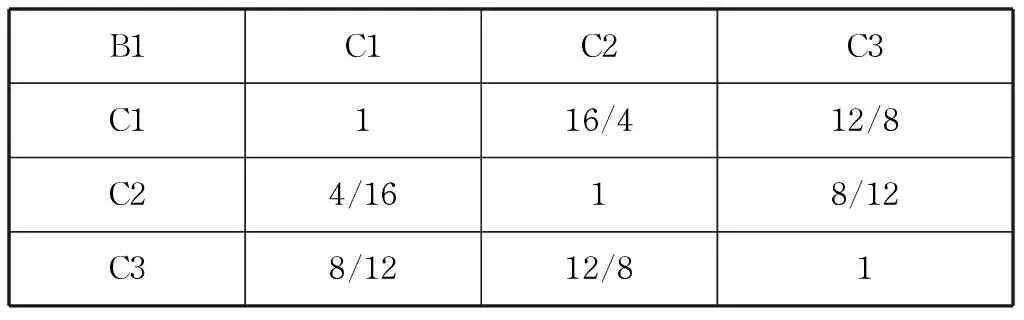
表3 判断矩阵 B1-C和权重Tab.3 Judgment matrix B1-C and indexes’ weight
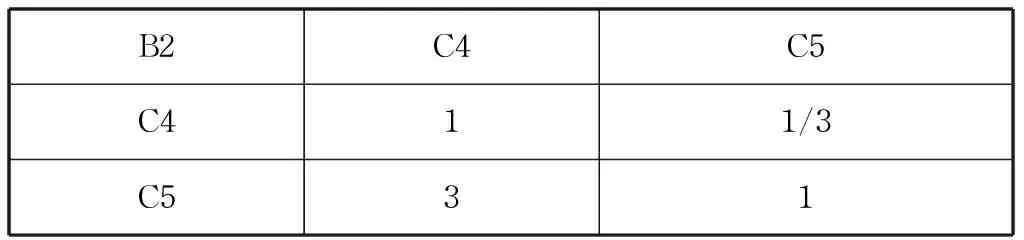
表4 判断矩阵 B2-C和权重Tab.4 Judgment matrix B2-C and indexes’ weight
则有判断矩阵
(15)
按照AHP的步骤计算得到的权重为
(16)
对上述权重做一致性检验,得到的CRB1=0.035 6<0.1。对1阶和2阶矩阵,总是完全一致的,此时CRB2=0。所以该权重是可以接受的。
综上,得到相似度评估模型的指标权重如表 5所示。对上层节点的相似度分析结果使用指标综合方法进行计算,计算结果如表 5所示,得出目标仿真模型的相似度为75.5%。

表5 相似度计算结果Tab.5 Results of similarity calculation
4 结束语
本文根据相似性原理,通过目标仿真模型特征分析,建立了相似度评估模型,研究了基于AHP的相似度评估方法,利用实测数据对半实物仿真系统中的目标仿真模型相似度进行了分析。算例结果表明,该方法能有效降低单一指标进行相似度评估所带来的风险,为仿真模型的验证提供了参考依据。
