基于IFOA算法的路基边坡动态预警研究
2020-12-25朱家剑丁龙亭付林杰王选仓高文泽
朱家剑,丁龙亭,付林杰,王选仓,高文泽
(1.甘肃路桥第三公路工程有限责任公司,甘肃 兰州730030;2.长安大学 公路学院,陕西 西安 710064;3.天津市市政工程设计研究院,天津 300392)
0 引 言
随着我国山区公路里程的增加,出现了大量的高填深挖路段,这对公路边坡稳定性提出了更高的要求,一旦路基边坡失稳,不仅会危及行车安全,而且还会影响道路通行能力,严重影响经济效益。如果在边坡滑坡前能够及时监测到并做出预警,将会有效降低道路行驶车辆所受到的威胁,可极大地减少人员伤亡和财产损失。
目前,我国很多学者都对边坡监测技术进行了研究。霍欣杰等[1],王堃宇等[2]借助三维激光扫描技术获取边坡表面任何时刻的变化状况,通过监测边坡表面的总体变形趋势实现边坡的监测预警;蔡明娟等[3]、代朵等[4]通过北斗系统对边坡进行动态监测,预测灾害的发生。这些技术只能监测边坡表面土体位移变化,无法得知边坡内部土体结构的稳定性。孙健[5]、马豪豪等[6]提出将光纤光栅位移传感器布设在露天矿开采潜在滑动面上对位移数据进行精确采集并预警的方法;路亚妮等[7]、宋丹青等[8]以实测的位移、温度、降雨量和时间作为影响边坡长期变形的因素,根据偏最小二乘法确定各影响因素的权重,基于模糊神经网络方法建立了边坡典型监测预测模型,可以对高边坡施工危险性进行有效预警;孙光林等[9]、王钦亭等[10]运用物联网技术,研发了边坡灾害监测预警物联网系统,解决了倾斜顺层岩质边坡监测预警所面临的预测困难、监测布点繁多等难题,完善了监测预警模式,实现了对灾害的超前预警;王俊等[11]、王俊杰等[12]基于无限边坡算法构建了简单的实验室降雨型滑坡技术性预警系统,通过模型试验结果,对预警系统的预警能力进行了分析,该模型准确性较好;贺可强等[13]、张振华[14]在系统分析蠕滑型边坡不同蠕滑变形阶段的变形演化特征与损伤破坏机制基础上,运用损伤力学基本原理,确定了边坡的蠕滑位移与其坡体损伤变量及其稳定性系数的定量关系,并依此建立了基于边坡蠕滑位移参数确定其动态稳定性系数的方法,对蠕滑性边坡的稳定性评价和预测有一定的实用性和有效性。
国内学者大多将传感器埋置在潜在滑动面上,并没有找到边坡上最危险的滑动面,对传感器监测结果的可靠性有一定影响。因此,本文采用IFOA算法对位移传感器的布设位置进行了优化计算,确定了传感器最佳布设方案,并以此对边坡变形进行监测,实现边坡预警,并针对不同预警级别提出了响应措施。
1 依托工程边坡调查分析
1.1 依托工程概况
渭武高速公路是兰海高速公路在甘肃省境内的重要组成部分,北接在建的临洮至渭源高速公路、已建成的兰州至临洮高速公路,南接已建成的武罐高速(武都至罐子沟),是甘肃省通达四川、重庆、贵州等出海通道的重要南出口公路,也是西北地区与西南地区间最为便捷的交通要道。
试验段沿线主要为构造剥蚀中低山区,地势总体北高南低,地表覆盖中厚层马兰黄土,下部为离石黄土,具孔隙、湿陷性,湿陷等级为Ⅲ级(严重)湿陷,天然含水量平均值为5.3%~21.9%,压缩系数平均值为0.28 MPa-1,压缩模量平均值为8.82 MPa。高边坡路段分布较多,边坡工程统计见表1,试验路现场边坡如图1所示。

表1 边坡工程统计表Tab.1 Slope project statistics table

图1 试验路现场边坡Fig.1 Test road scene slope
1.2 依托工程边坡调查
本文依托工程对边坡监测预警展开研究,通过调查渭武高速K226+369~K234+140路段的边坡土质、高度及分级情况,证明对路基高边坡采取监测措施的必要性。其边坡分布情况见表2和图2。
由表2和图2可知,调查路段挖方边坡高度较大,其中,高20~30 m的边坡占全部挖方边坡的25.71%,高30~40 m的边坡所占比例为22.86%,50 m以上边坡所占比例为31.43%,边坡高度20 m以上的挖方边坡占全部挖方边坡的85.7%。该路段富含Ⅱ级自重湿陷性黄土,大孔发育,植被不发育,因此,在路基开挖过程中要特别注意边坡开挖稳定性,采取必要的加固措施并结合动态监控手段,保证路堑边坡的稳定性。

表2 渭武高速路基边坡汇总Tab.2 Summary of the subgrade slope of Weiwu expressway
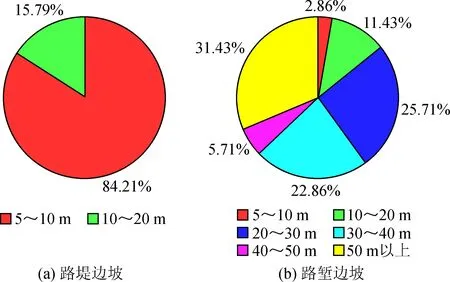
图2 路基边坡高度分布图Fig.2 Height distribution map of subgrade slope
2 边坡监测系统
2.1 IFOA算法
IFOA是基于果蝇觅食行为得到的算法,通常被用于寻求全局最优解[7]。果蝇觅食过程如图3所示。
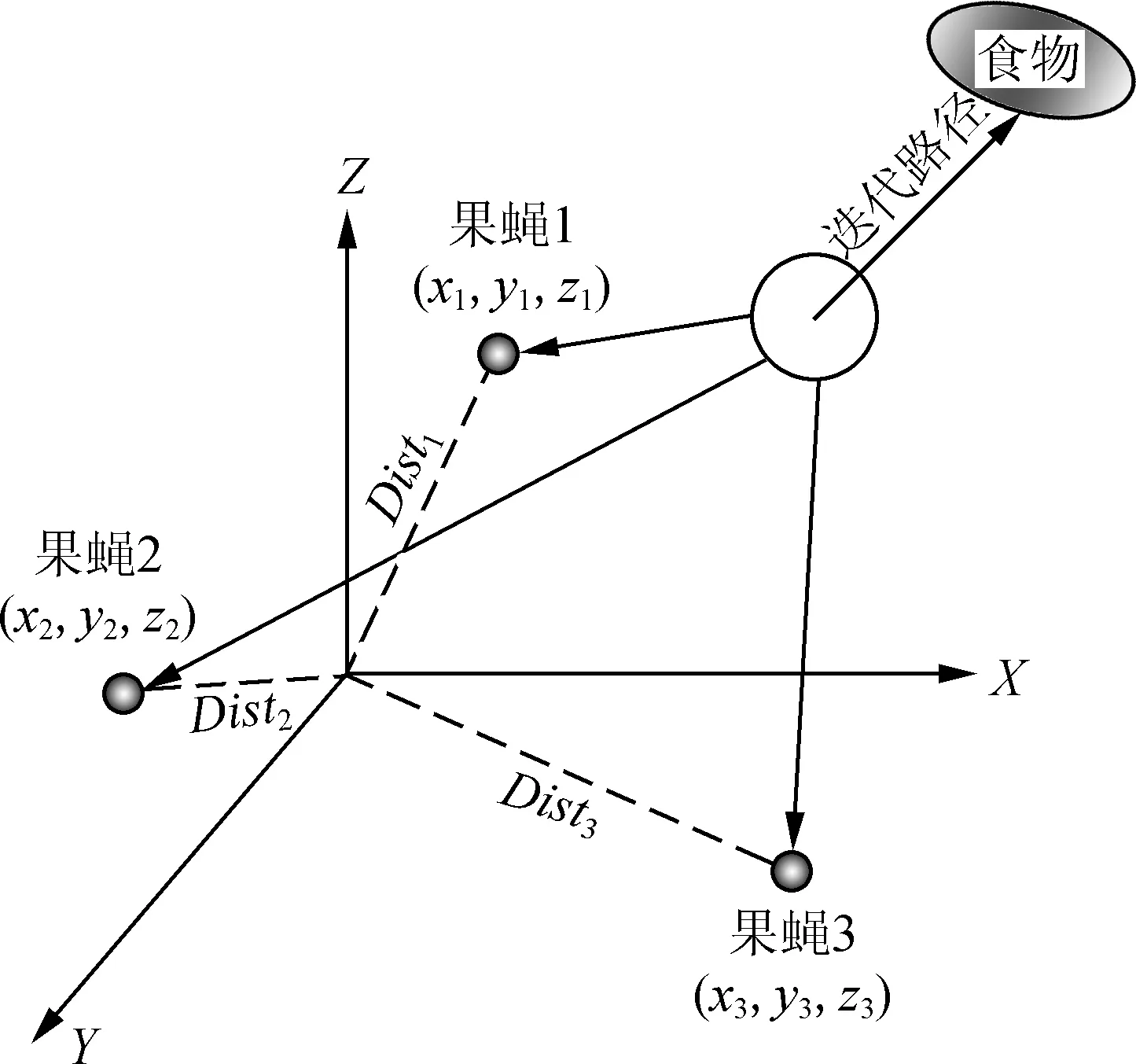
图3 果蝇觅食过程Fig.3 Foraging process of the fruit fly
IFOA算法过程如下:
(1)初始化算法参数。设果蝇规模为Spop,最大觅食代数Mgen,果蝇群初始坐标为(X0,Y0,Z0)。
(2)单个果蝇寻找食物的方向和飞行距离为

(1)
式中:L0为初始步长值,mgen为当前觅食代数,i=1,2,…,Spop。
(3)由于食物源具体位置未知,因此利用式(2)计算第i个果蝇当前位置与原点的距离Disti,从而得到味道浓度判定值Si。

(2)
Si=1/Disti。
(3)
(4)将Si带入味道浓度判定函数中,可得到其当前位置的味道浓度。
Smelli=function(Si),
(4)
(5)根据式(5)得到所有果蝇当前味道浓度最高的个体。
[bestSmell,bestIndex]=max(Smelli)。
(5)
(6)根据当前味道浓度最高的果蝇所在位置坐标,将其作为食物源所在位置,其他果蝇可根据视觉寻找该食物源,食物源位置由式(6)确定,

(6)
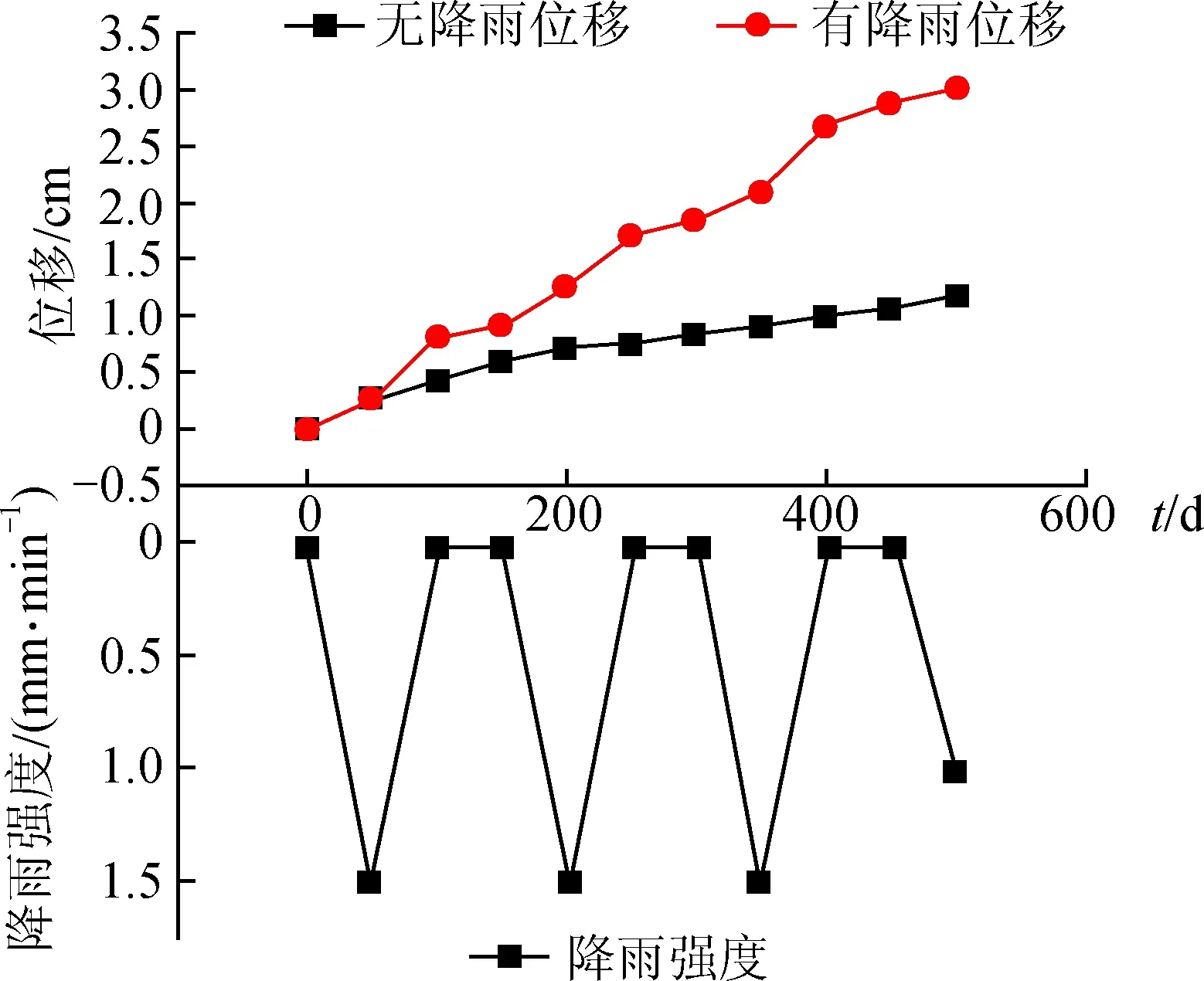
(7)重复步骤(2)~(5),进行寻优迭代过程,并判断当前味道浓度最大值是否大于前一迭代过程味道浓度最大值,同时满足mgen (1)初始化IFOA参数。设有Spop个监测点的最终位置位于边坡最危险滑动面上,其初始坐标为(X0,Y0,Z0),最大迭代步数Mgen,且Spop不小于最终布设的传感器数量。 (2)赋予每个监测点相对初始位置移动的方向和距离,采用递减搜索步长代替固定步长,得到(Xi,Yi,Zi),假设当前各监测点所在曲面为最危险滑动面,其上土体为滑动体,以当前各点为分界将滑动体分成单元体,此时滑动体三维受力图见图4。 根据滑动体受力图可得,第i到第(i+1)个监测点间滑动体在di-1,i方向上抗滑力矢量和为 图4 滑动体三维受力图Fig.4 Three-dimensional force diagram of the sliding body 式中:Σ为滑动面;c为土的黏聚力;φ为土的内摩擦角;δ为极限剪力与位移方向的夹角;di-1,i为滑动方向,由式(8)确定;ni-1,i为其法向量;m为地基比例系数;ω为di-1,i与ni-1,i的夹角,i=1,2,…,Spop。 di-1,i=(Xi-Xi-1,Yi-Yi-1,Zi-Zi-1), (8) 第i个到第(i+1)个监测点间滑动体di-1,i方向上下滑力矢量和为 Ri-1,i=|Ri-1,i|cosν, (9) 式中,Ri-1,i为作用在该滑动体的合外力。 该滑动土体的稳定系数为 (10) (3)根据式(10)得到目标判定函数,见式(11)。 [bestSmell,bestIndex]=min(Fs(i-1,i))。 (11) (4)保留当前各监测点的位置坐标及其对应稳定系数,此时各监测点所在位置是边坡稳定系数最小的位置,即边坡最危险滑动面位置,见式(12)。 (12) (5)进入迭代寻优过程,重复步骤(2)~(3),判断当前稳定系数是否小于前一迭代过程稳定系数,且mgen 利用Spop个监测点确定最危险滑动面后,最终传感器的布设位置可选择在各监测点位置。为了使计算得到的最危险滑动面位置更准确,需要布置尽可能多的监测点,但是若在每个监测点都埋设传感器,一方面需要对边坡岩土体进行多个位置的开挖,这会对边坡原有的岩土体结构造成较大破坏,另一方面部分监测点相距过近,它们对土体的监测范围大部分重合,可以用一个监测点代替。因此有必要在现有监测点中选择最佳监测点,以此作为传感器最终布设位置。 根据式(12)得到各监测点的最终位置坐标和其对应滑坡体的稳定系数后,设s为相邻传感器间的最大布设距离,取值需根据实际使用的传感器型号、边坡土质情况、边坡高度、边坡水文地质条件及气候条件等因素确定。此时,根据式(13)确定传感器布设位置坐标(Xj,Yj,Zj)。 (13) 由式(13)可得到传感器布设最佳位置,此处为距离小于s的所有监测点中稳定系数最小的监测点的坐标。 在确定位移传感器布设方案后,边坡土体内部位移可作为其预警指标,考虑到实际工程中,一方面降雨会在土质边坡表层产生坡面水流,破坏边坡表层土体结构,严重时可能会引起滑坡[15-16];另一方面雨水入渗会造成边坡岩土体孔隙水压力增大,降低其抗剪强度,从而影响边坡稳定性[17-18]。因此,本文在确定边坡监测预警指标时,将降雨强度、边坡位移-时间曲线特征和位移量作为预警指标。 本文利用边坡室内模拟试验,通过监测不同时间、不同降雨强度下的边坡变形进行预警分级。在人工降雨装置下方先砌筑长14 m,宽2.75 m,高1.5 m的矩形实心平台,以便集流。在矩形平台上按相似比1∶1制作试验槽,坡长为8 m,坡度为1∶1.5,采用黄土填筑,顶端设有长1 m近于水平的缓坡段(坡度为3%),用于模拟土路肩冲刷。 试验在西安理工大学人工降雨大厅进行。该人工降雨装置距地面净高12 m,有效降雨范围长14 m,宽2.5 m。由于主要模拟暴雨,采用X型下喷式喷头,并在母管上安装电磁阀以实现快速切换控制。研究区为我国黄土地区,降雨多为集中且雨强较大的暴雨,根据该地区降雨特征,试验中人工模拟降雨也以短历时、高强度暴雨为主,3个基本雨强为0.5,1.0,1.5 mm/min,试验最小雨强为0.26 mm/min(我国气象部门规定60 min降雨量超过16 mm或24小时内降雨量超过50 mm为暴雨),最大雨强为2.6 mm/min。 模拟试验成功与否的理论基础是模型与原型的相似程度。边坡冲刷模拟试验的基本思想是采用与原型物理力学性质相似的材料,按照一定几何比例模拟边坡在降雨情况下发生侵蚀,并满足相似的边界条件和初始条件,在相似时段内形成相似的坡面冲刷现象,通过测量和分析试验结果,以期对边坡冲刷量预测计算、边坡几何设计、防护设计和养护维修提供科学依据。 在规划模拟试验时,应遵守下列相似条件:几何相似;物理现象相似;初始和边界条件相似;各同名无因次参数相等。 (1)黄土物理性质试验。主要测定试验用黄土的粒度成分、含水量、密度,并进行击实试验。 (2)填筑土层。按压实度要求将黄土晾晒或适当洒水,控制土的含水量,用自装的安全索吊运土,分层铺填于模型槽中,用立式振动电夯分层压实,用环刀法测定和控制土的压实度。压实后土坡超厚15~20 cm,然后削坡、整平。 (3)测定降雨强度。试验前,根据降雨试验拟选用的雨强反复进行测定,直到雨强大小及其均匀性都满足要求。 (4)传感器埋设与结果。根据上述传感器布设方案,在边坡最危险的滑动面上埋置4个位移传感器,试验边坡模型如图5所示,根据传感器位移平均值,得到边坡位移与时间、降雨强度关系曲线如图6所示。 图5 室内边坡模型Fig.5 Indoor slope model 图6 边坡位移与时间、降雨强度关系曲线Fig.6 Relation curves of slope displacement and time,rainfall intensity 由图6可知:降雨强度对边坡位移-时间分布曲线有较大影响,0~100 d内,边坡处于初始变形阶段,随着降雨强度增大,边坡变形速度随时间加速增长,这与无降雨时边坡s-t曲线初始变形阶段特点不同,说明过大的降雨强度会使边坡初始变形阶段由减速运动变为加速运动;100~500 d内,边坡处于s-t曲线稳态变形阶段,但与无降雨时边坡s-t曲线特点不同的是,边坡变形速度随着降雨强度增大也有明显变化,且变形速度变化略滞后于降雨强度增加,根据这一特点,可根据降雨强度对边坡变形监测作出提前预测。根据边坡位移与时间、降雨强度关系曲线,采用降雨强度、边坡s-t曲线特征和边坡位移量为边坡预警指标,得到边坡各级预警和响应措施,如表3所示。 本文采用IFOA算法对位移传感器的布设位置进行了优化计算,确定了传感器最佳布设方案,以此对边坡变形进行监测,实现边坡预警与响应。主要研究结论如下: (1)通过调查渭武高速公路边坡分布情况,发现50 m以上路堑高边坡占有比例大,有必要采取加固措施并结合动态监控手段,保证路堑边坡的稳定性。 表3 边坡各级预警及响应措施Tab.3 Early warning levels and response measures for slopes 注:各级预警满足任一预警指标时应立即启动该级预警响应 (2)基于IFOA算法对边坡最危险滑动面位置进行了迭代寻优计算,确定了最危险滑动面位置,并结合边坡土质情况、边坡高度、边坡水文地质条件和气候条件等因素确定了传感器布设方案。 (3)结合降雨对边坡的冲刷和入渗作用,通过分析不同降雨强度下边坡位移-时间曲线的变化特点,以降雨强度、边坡s-t曲线特征和边坡位移量作为边坡预警分级指标,并针对不同预警级别提出了响应措施。 (4)研究成果实现了高陡边坡稳定性检测预警与响应,保证了施工安全,也为高边坡设计方案的优化提供了依据。下一步将把研究成果应用于实际工程,确定研究成果的可行性与实际意义。2.2 基于IFOA算法的最危险滑动面确定
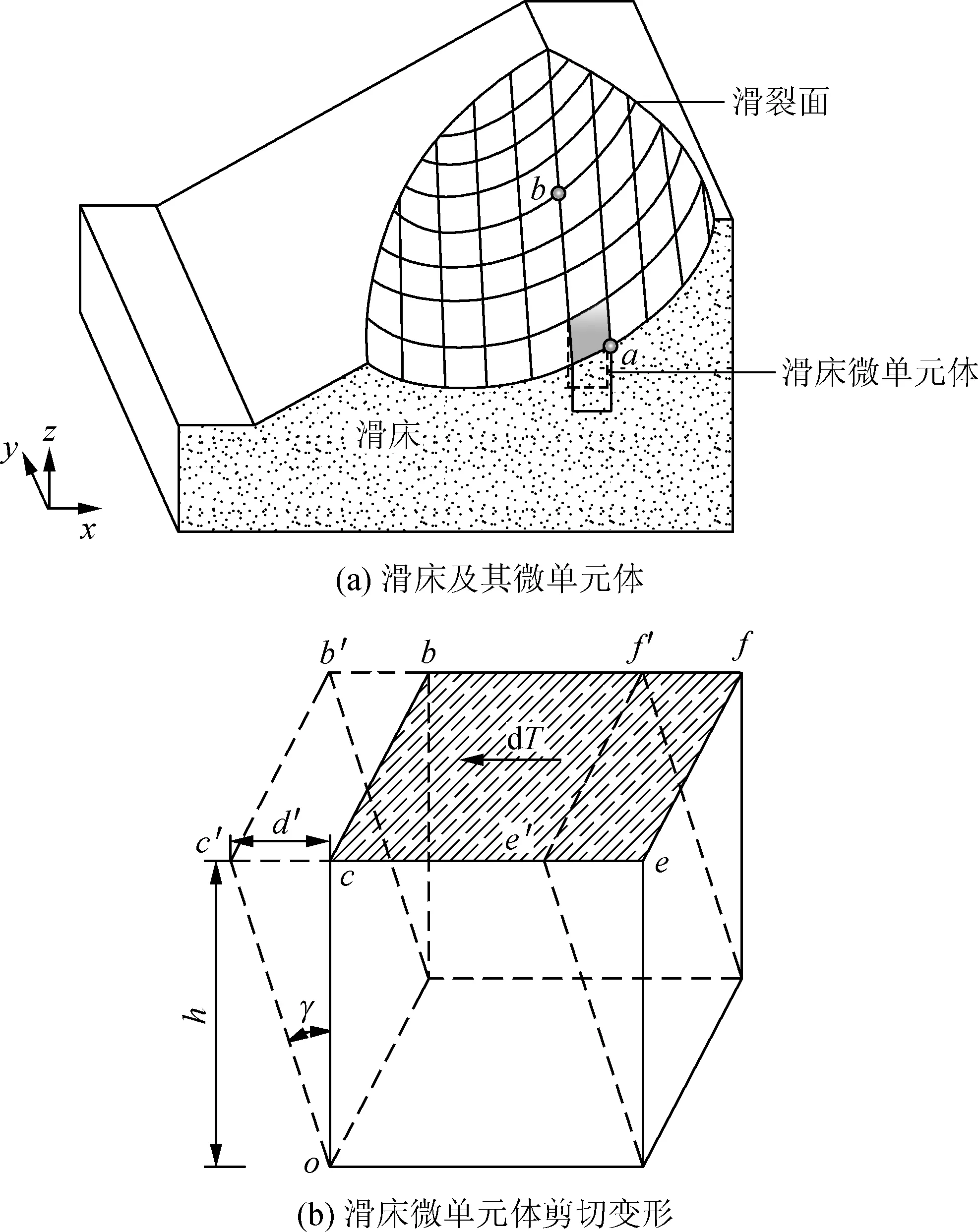

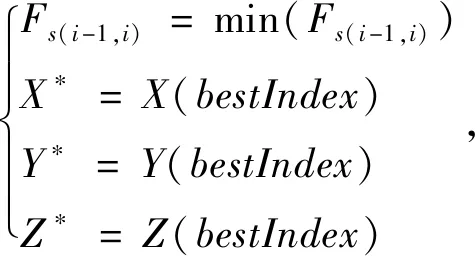
2.3 传感器布设
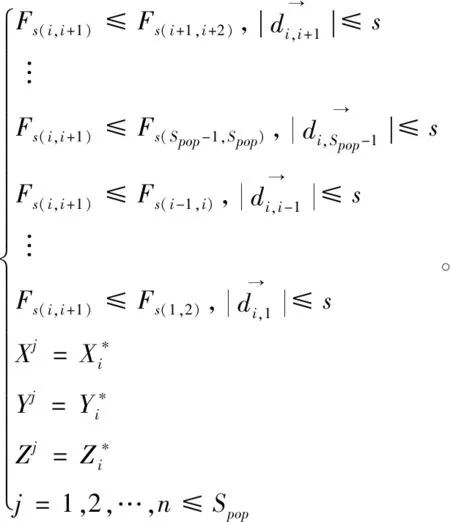
3 边坡监测预警分级
3.1 试验模型设计
3.2 边坡冲刷模拟试验相似性讨论
3.3 试验过程与结果讨论

4 结 论

