工程船舶开口角隅区域形式优化及疲劳分析

2020-12-25陈佰川

石油工程建设 2020年6期

陈佰川

1.天津大学水利工程仿真与安全国家重点实验室，天津 300072

2.天津大学天津市港口与海洋工程重点实验室，天津 300072

在工业生产中，很多特殊用途结构物在制造过程中会设置局部开口以满足某种实际需要，如海洋平台的月池以及特种舰船的舷侧和甲板开口等。据统计，一艘大型舰船在其服役期的20～25年内，承受的应力循环次数可高达107～108次之多[1]，而疲劳破坏是大型工程结构物的主要失效模式之一[2]。因此，结构物的制造工艺、外形和尺寸对疲劳破坏的影响是在设计中必须考虑的因素之一。

针对开口结构角隅处的形状优化问题，韩春生[3]通过谱分析，研究了增设肘板和增加板厚对开口角隅处应力集中程度的影响；李霞丽[4]研究了在船舶甲板开口附近增设围缘扁钢的尺寸对角隅应力的影响；程玉芹[5]通过建立三舱段模型，对某舱口椭圆形角隅进行了形状优化。Remes[6]针对开口部位研究了材料表面完整性对高强度钢疲劳强度的影响。对于疲劳裂纹扩展问题，李国辉[7]通过预应力计算，预测了某钻杆的疲劳寿命；胡艳华[8]对隔水管道进行了全尺寸试验并观察了疲劳断口；唐昕[9]对储气井的套管和管箍进行了应力计算和疲劳分析；余建星[10]基于柔度法，对自主设计的开口角隅试样进行了裂纹扩展参数数值计算。

本文选取某海洋石油工程作业船舶的舷侧钢板矩形开口为研究原型，首先利用有限元分析软件对不同尺寸的圆形和椭圆形角隅进行了应力分析，进行了优化选择，并探究了角隅应力的影响因素。随后设计了多级应力水平模拟轴向加载并进行了平均应力修正，利用疲劳分析软件FE-SAFE对若干角隅形式进行疲劳分析，拟合出优选角隅形式的理论双对数S-N曲线，以供开口角隅结构设计时参考。

1 舷侧钢板开口应力集中

大型工程结构物在工业制造过程中，由于工艺、技术以及材料不均匀等原因，不可避免地会有夹渣、气缝和初始裂纹等初始缺陷产生，特别是在焊缝和应力集中部位[1]。

海洋石油工程作业船舶常在舷侧设置局部大开口而导致出现严重的应力集中现象，从而显著地影响了舷侧钢板架的整体强度和疲劳寿命，这就要求船厂在钢板制造前针对大开口尺寸和样式谨慎地进行优化设计。图1为海洋石油工程勘探船舶舷侧开口钢板架的应力集中情况数值计算云图。

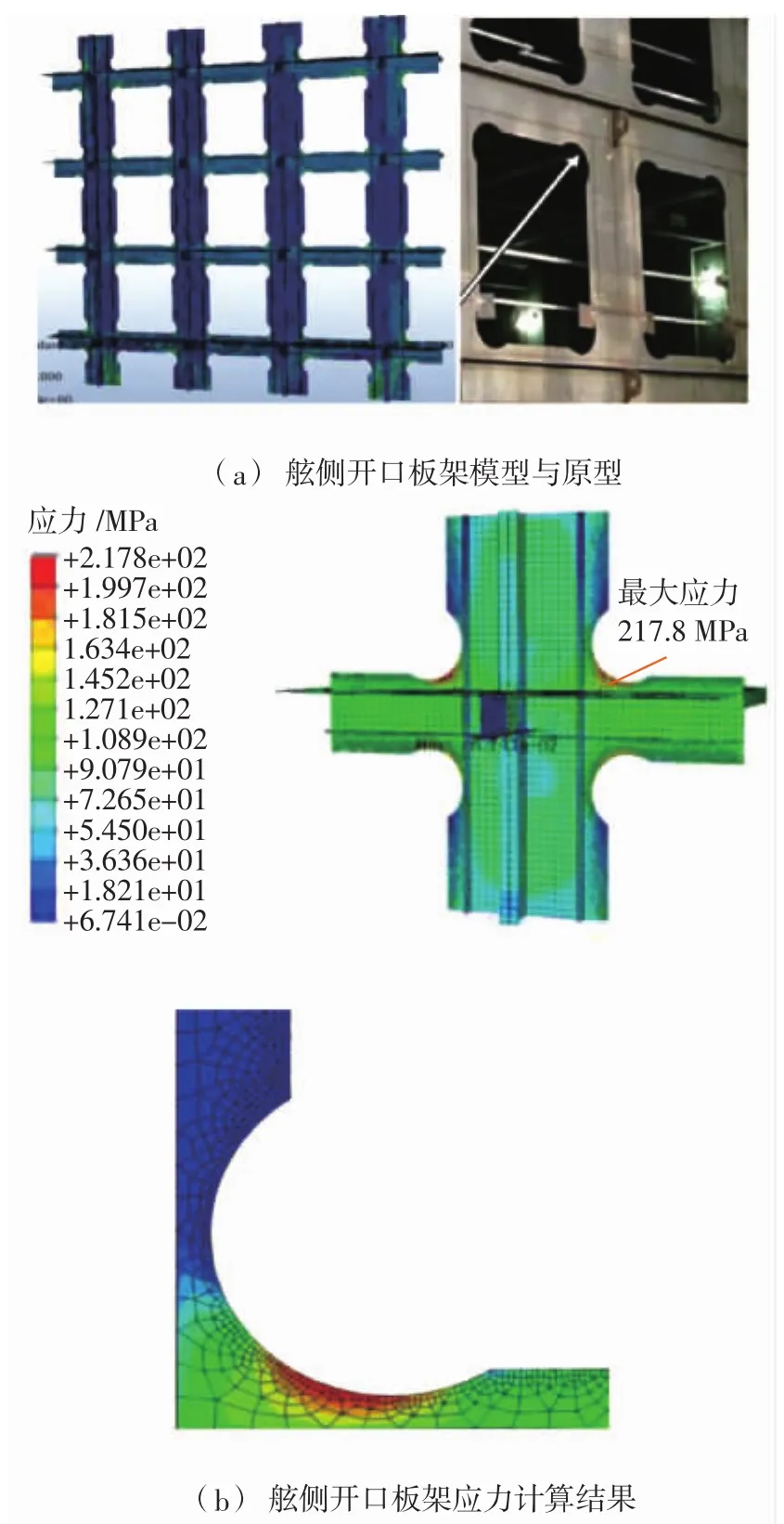
图1 应力集中数值计算云图

由图1可见，开口结构的角隅区域由于几何不连续而导致的应力集中情况较为严重，远大于该结构其他区域的应力，所以开口结构的角隅处是疲劳强度设计和形状优化的重点区域。

2 平板开口试样数值计算

2.1 平板开口试样模型建立

2.1.1 试样基本参数

针对开口角隅形状优化问题，本文设计的平板开口试样以多功能作业船舷侧钢板的矩形舷窗开口为原型，利用有限元分析软件对多组缩比尺模型进行试算后，确定试样基底平板为长50 mm、宽60 mm的矩形，平板中央开口按照舷侧开口原型尺寸缩小约80倍后取整，即开口矩形长26 mm、宽为22 mm。研究材料选择船舶常用型钢Q345钢材，其材料参数如表1所示[11]，开口区域的原型和数值模型如图2所示。在平板中央开口的上方和下方各预留一直径为9.5 mm的圆孔，并将上圆孔的圆心设置为加载耦合点，为后续研究提供基础数据和参考。

表1 Q345钢材材料参数

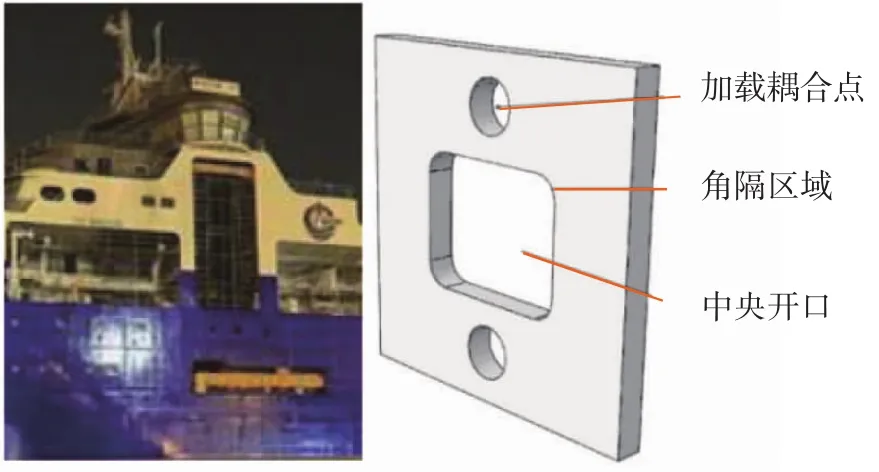
图2 平板开口试样原型与数值模型

2.1.2 边界条件和网格划分

为模拟试样轴向拉伸时的疲劳受力状态，将上圆孔内表面的受力和位移耦合到圆心处，所有角隅形式的模型均在上圆孔加载耦合点处施加1 000 N竖直向上的力，在下圆孔内表面设置完全固定边界条件。将模型按照角隅区域特点切割后，全局采用结构化六面体完全积分单元的网格划分方式，全局网格单元几何尺寸设置为0.8 mm，其中开口角隅处为重点研究区域，在四个角隅处需要将局部网格尺寸细化为0.4 mm。由于角隅处采用六面体结构化网格划分时效果不佳，为了保证角隅处网格与模型主体网格平滑过渡，将四个角隅处网格属性设置为六面体为主的扫略网格，如图3所示。模型网格尺寸在加密前后计算结果仅相差1.2%，满足计算精度要求，网格收敛性较好。

图3 试样网格划分

2.2 开口角隅优化形式的确定

舷侧钢板的矩形开口在角隅处一般采用弧形过渡，本文选取椭圆形和圆形角隅进行对比研究。为了控制变量，在进行形状比较时需要遵循等效性原则，即两种开口角隅形式所占用的侧板开口的面积相等，也即两者在制造时的钢板用量相同。开口角隅处需遵循的计算条件如图4所示。为满足等效性原则，只需使两图中的阴影面积相同即可，则其中一个角隅处需要满足的关系式为：

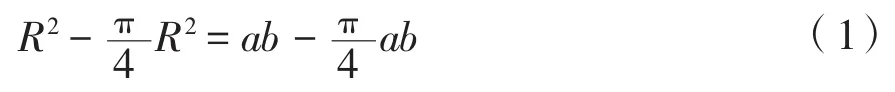
式中：R为圆形角隅半径；a为随圆长半轴，b为随圆短半轴。

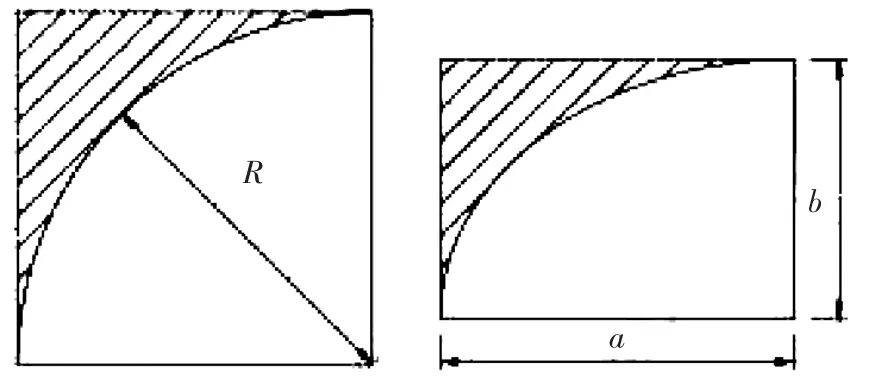
图4 开口角隅处等效性原则示意

现设a为常数且为5 mm，则b和R为变量。为研究采用椭圆和圆形角隅时的应力对比，进一步规定圆角半径R依次取为2.6～5.0 mm不等。将所取圆角半径R的值分别代入式（1）后，相应的椭圆短半轴长度b以及椭圆度a/b的值也就相应确定下来。

2.3 角隅处应力数值计算结果

平板开口试样的计算组次设置及应力数值计算结果见表2，其开口角隅处的应力曲线图和有限元应力分析云图示例分别如图5（a）和图5（b）所示。为了避免模型缩比尺前后的尺寸效应对应力分析结果的影响，采用椭圆度a/b和圆角半径R与开口矩形长边l的比值R/l这两个无量纲数，来描述角隅尺寸和形式变化过程对角隅处应力集中情况的影响。

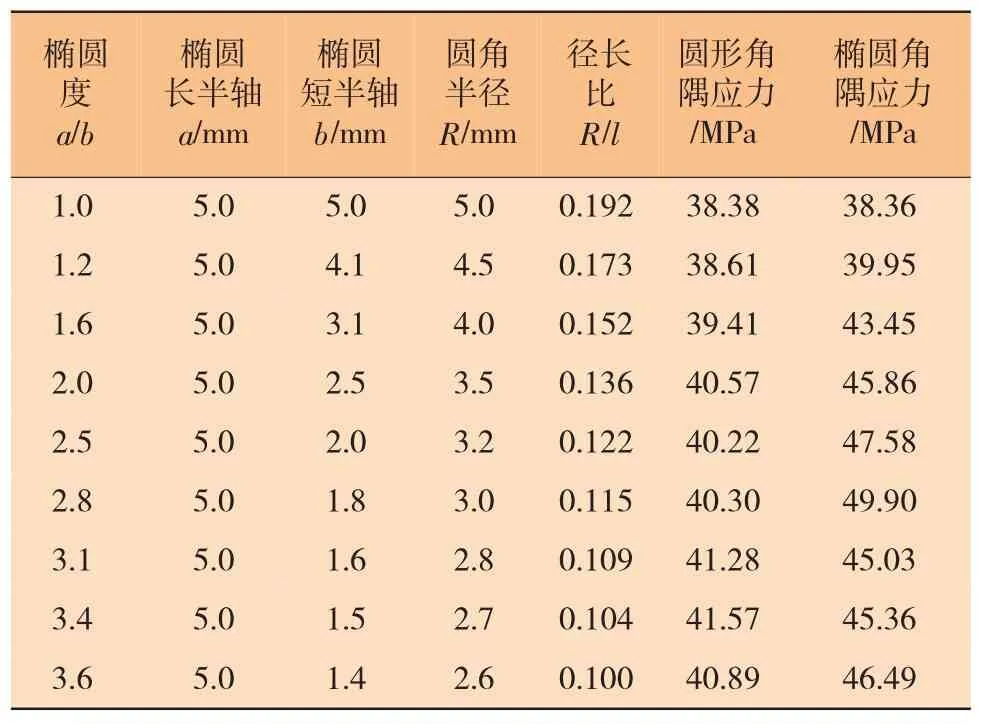
表2 角隅应力有限元计算结果

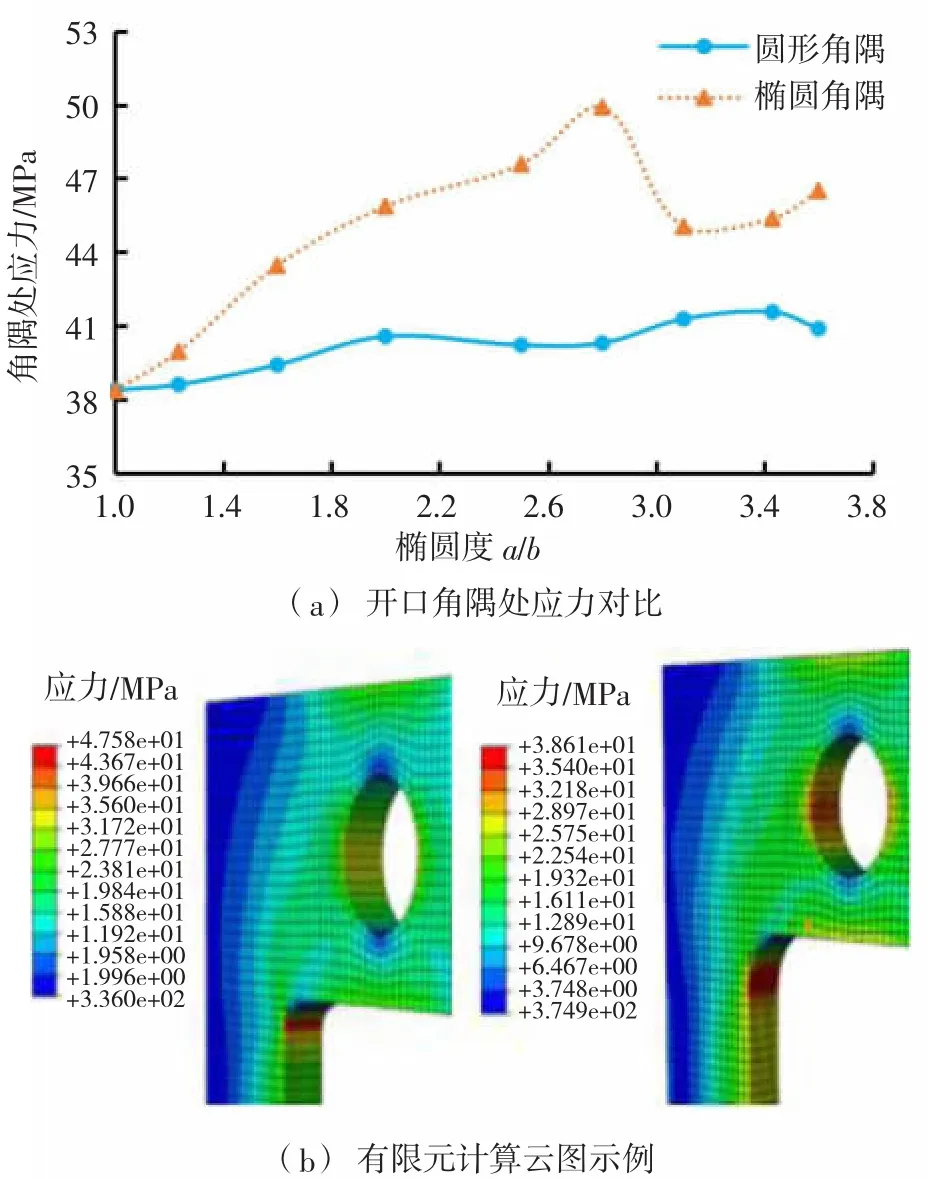
图5 开口角隅处应力分析计算结果

有限元应力计算结果表明：在保证开口面积相同的情况下，采用圆形角隅时的最大应力总小于椭圆形角隅；随着圆形角半径R的增大，圆形角隅处的应力并非单调下降，而是有一定起伏波动，但总体仍呈下降趋势。随着椭圆形角隅的椭圆度a/b的不断增大，角隅处最大应力整体呈上升趋势，在a/b=3.1附近会有一个极小值点。如果某些开口结构需要采用椭圆形角隅，可选择椭圆度a/b=3.1时的角隅形状作为工程上的优化选择。考虑工程实际和美观需求，圆形角隅的半径R也不能过大，否则可能影响正常使用，可选取径长比R/l=0.192时的圆形角隅作为优选设计，此时应力集中情况较低，在承受相同的荷载时，可以获得更长的疲劳寿命。

2.4 角隅应力影响因素探究

在角隅形式确定的情况下，钢板本身的厚度、开口相对长度和开口长宽比等也会影响开口角隅处应力的大小。本节建立若干模型对以上影响因素进行了研究，其数值计算结果如图6所示，图中数据均以在开口角隅处取R=5 mm的圆弧为前提。

如图6（a）所示，随着试样厚度的逐渐增加，角隅处应力呈非线性降低，可用二次函数来表达厚度对开口角隅处应力的影响。由于矩形舷窗开口原型的长宽比为2 050 mm/1 732 mm=1.18，故保持模型开口长宽比l/w=1.18不变，改变开口矩形长度l与基底平板长度L的比值，即改变开口的相对大小，可知随着相对开口长度l/L的逐渐增大，角隅处应力呈线性增长，如图6（b）所示。保持开口相对长度l/L不变，改变开口本身的长宽比l/w，可见随着l/w的逐渐增加，角隅处应力呈非线性下降，可用二次函数来表达开口长宽比对开口角隅处应力的影响，如图6（c）所示；另外，在此图中l/L=0.48和l/L=0.52两曲线在横坐标相同时，相应纵坐标之间的差值相等，且l/L越大，角隅处应力越大，进一步证明了开口相对长度对角隅处最大应力的影响是线性增加的。

3 角隅模型疲劳分析

3.1 平均应力修正

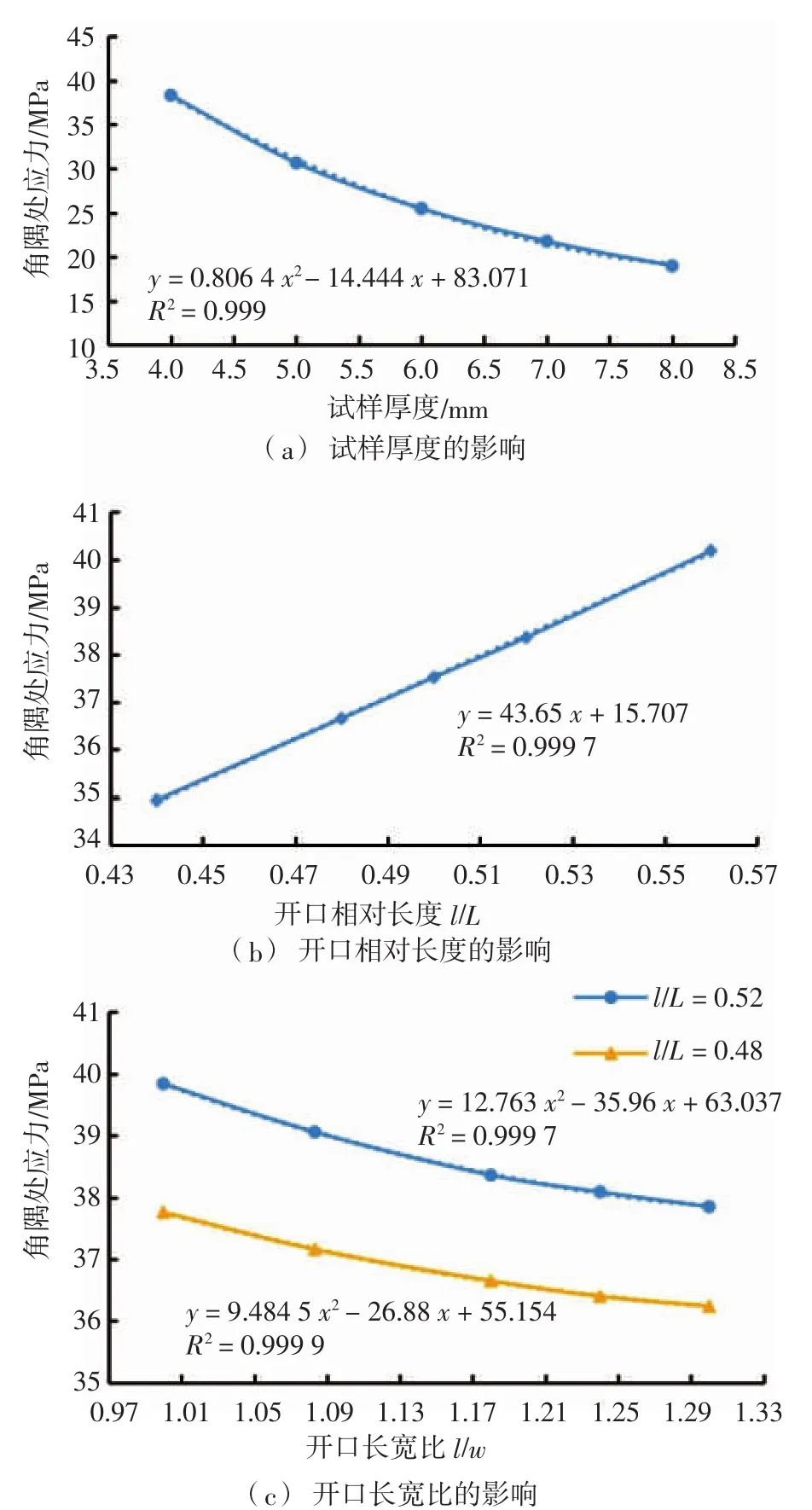
图6 角隅应力影响因素计算结果

通常情况下，通过疲劳试验和理论分析得到的S-N曲线，都是在受平均应力σm=0的对称循环轴向拉伸荷载（应力比=-1）的应力条件下绘制的。在采用疲劳分析软件FE-SAFE时，应将设计应力等效转化为对称荷载，然后再进行疲劳分析，常用的疲劳极限方程有Goodman直线方程、Soderberg直线方程和Gerber抛物线方程[12]，如图7所示。

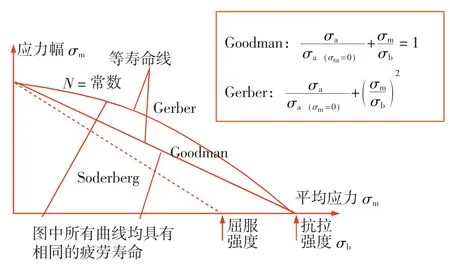
图7 疲劳极限方程曲线

本文选择经典的Goodman平均应力修正法，认为疲劳极限线是经过对称循环应力的疲劳极限点和静强度点的一条直线，其直线方程可表达为：

式中：σ-1为修正后的对称荷载应力幅，σa为修正前设计荷载应力幅，σm为修正前设计荷载平均应力，σb为材料极限抗拉强度。

3.2 疲劳计算

选择R分别为5 mm、4 mm和3.5 mm的圆形角隅模型，以及椭圆度a/b=2的椭圆角隅模型，进行疲劳计算。首先在有限元分析软件中对加载点设置轴向拉力为1 N的荷载进行计算，采用与有限元分析时相同的单位制。选择7级应力水平模拟试样受多级轴向疲劳拉伸荷载，设计荷载的应力比取0.1。采用正弦波形的对称荷载进行应力加载，录入按照Goodman方法修正后的荷载幅，加载频率为2 Hz。表面处理形式为镜面抛光，采用默认疲劳算法进行疲劳分析。作为其中的优选形式，R=5 mm的圆形角隅模型加载设计和疲劳分析结果分别如表3和图8所示。

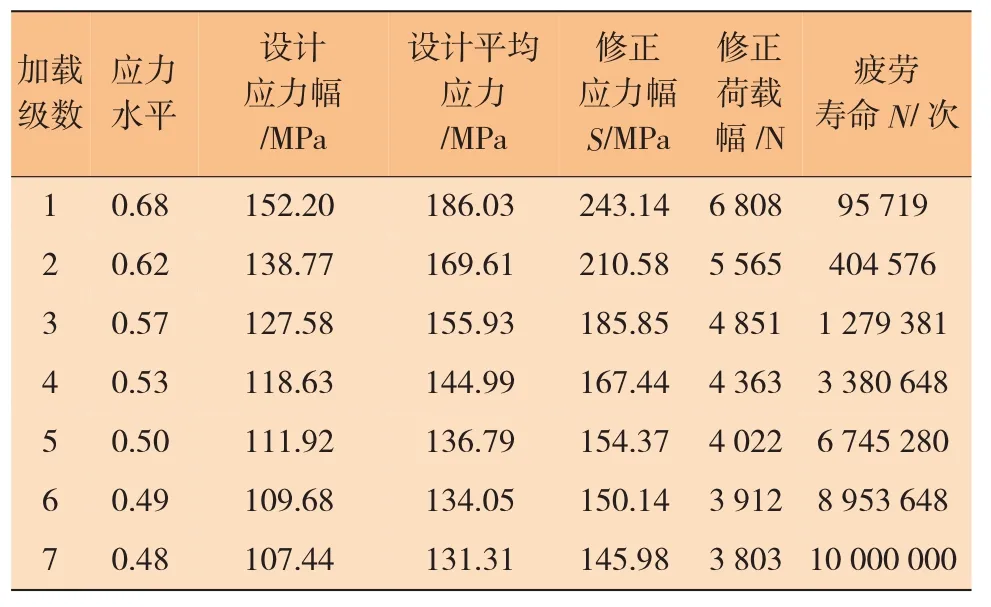
表3 FE-SAFE疲劳分析结果

3.3 S-N曲线

经过上述疲劳计算后，以Goodman修正应力幅S为y轴，疲劳循环次数N为x轴，可画出各模型角隅区域的理论S-N曲线。为了线性化表达，通常将直角坐标系转化为以10为底的双对数坐标系，以得到lgS-lgN的线性表达形式，如图9所示。

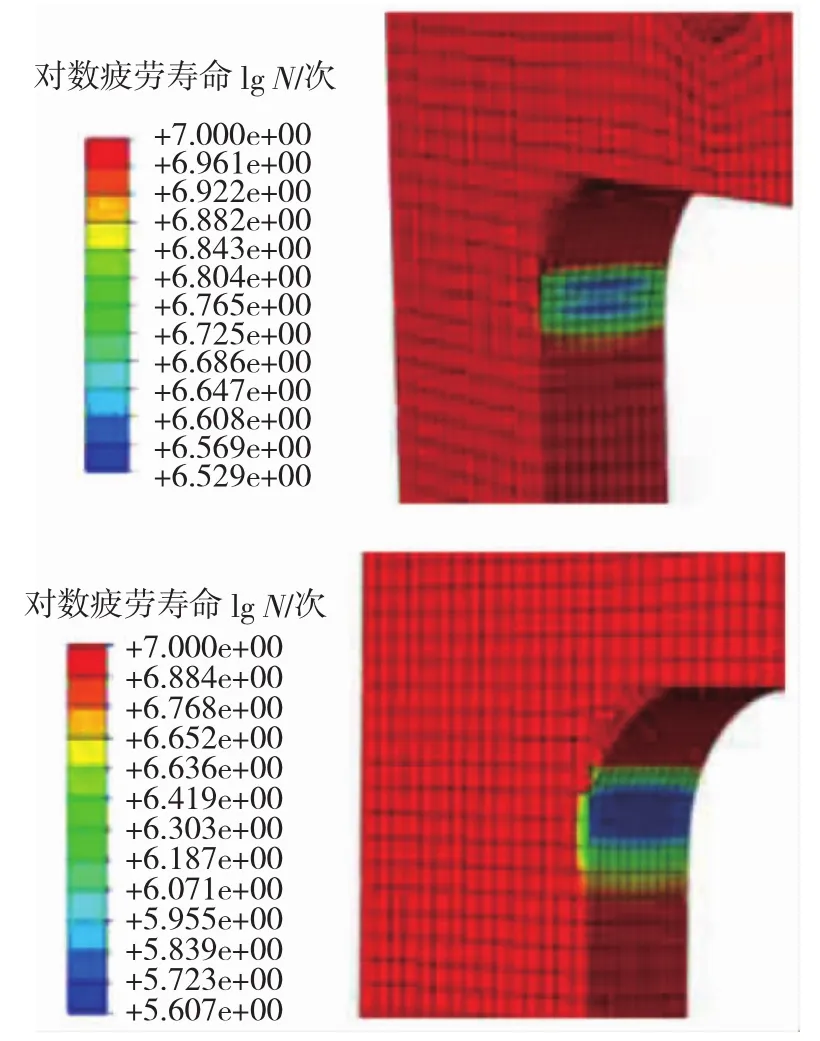
图8 FE-SAFE疲劳分析结果（R=5 mm）

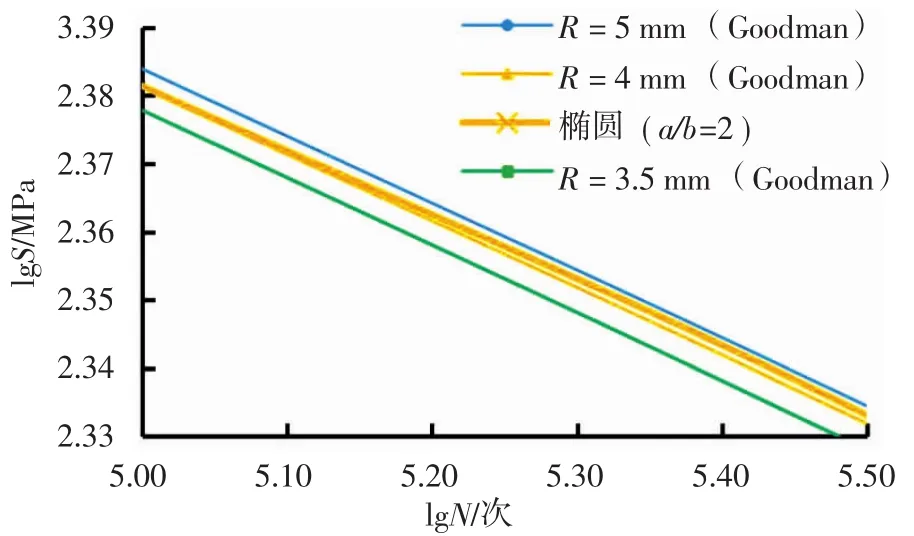
图9 角隅区域lgS-lgN曲线

由图9可以看出，在承受相同应力幅S的情况下，试样疲劳寿命由高到低排序依次为R=5、4、3.5mm的圆形角隅和a/b=2的椭圆角隅，且R=3.5mm的圆形角隅和a/b=2的椭圆角隅是尺寸等效角隅，疲劳分析所得结果与表2中的角隅应力计算结果排序是吻合的，进一步证明了所得结论的正确性。使用最小二乘法拟合疲劳分析数据后，可以得到径长比R/l=0.192（R=5mm）优选角隅形式的双对数线性表达式为lgS=-0.1113×lgN+2.945，R2=0.9942。