基于贪婪法的配电网负荷预测设计及其案例分析

韩一鸣， 马艳霞， 张坤， 胡志冰

(国网宁夏电力有限公司 经济技术研究院， 宁夏 银川 750002)

0 引言

为更好地应对当前复杂变化的经济发展状况，各电力企业应积极研究国家政策方向与整体电力市场环境的特点，从而对电力负荷的变化趋势实现精确预测的过程[1-3]。目前已有多种方法可以用于负荷预测，但在使用这些预测方法的时候还有许多缺陷需要解决[4-7]。例如，选择网格法进行负荷预测时需包含大量数据，可以利用归一化的参数预测来获得初始加速值，不过该方法所能达到的预测精度较低，需采取优化措施。针对以上问题，本文选择贪婪法预测得到配电网的网格负荷加速情况，之后开发得到了经过优化的软件，实现了预测速度的准确性的全面提升，同时也能够弥补之前由于初加速而引起的预测误差[8-11]。

采用贪婪算法对问题进行分析的方式是选择现有条件下的最优决策[12]。因此，即使贪婪法并未对所有的情况都考虑在内，其目标并是追寻整体最优解[13-15]，而实际上有很多问题都可以通过贪婪法进行求解获得整体最优解。贪婪法作为一种数据分析方法，已经被广泛应用于分析许多实际问题。考虑到现阶段国内外的经济形势呈现明显的波动性，由此引起电网负荷的大幅改变，同时越来越多的分布式电源也会引起电网负荷的较大变化，对于这种情况将难以通过网格法求解得到全局最优解，同时还会占用大量时间与资源，无法达到实时预测负荷与动态调整的效果[16]。根据以上分析，本文利用贪婪法的局部最优分析方式优化了网格的负荷预测过程。

1 模型建立

1.1 流程设计

贪婪算法的一个关键特征是采用无后效性的选择策略，表现为之前状态只取决于现有状态，而不会影响到后续过程[17-18]。因此对实际负荷进行预测的过程中，关于水平年负荷的预测先把输入的各个数据通过最优量度标准完成排序，之后根据实际排列的顺序输入相应的参数并完成检测过程。

贪婪算法的具体流程，如图1所示。

图1 贪婪算法流程

包括以下各步骤。

第一，选择最优化贪婪度标准。

第二，验证在上述标准下此问题可以满足贪婪选择性与最优子结构的条件。

第三，按照贪婪度量标准实施数据排序，确定贪婪选择算法，求解得到可行解的子集。

第四，根据贪婪序列以及目标函数计算得到最优解。

采用贪婪算法进行计算的流程如下。

Greedy(N) /*N为候选集合*/

{

S={}; /*初始解集是空集 */

while(notsolution(S)) /*集合S不属于问题的解*/

{

x=select(N); /*对候选集合N进行贪婪选择*/

iffeasible(S,x) /*判断含有x的集合S是否拥有可行解*/S=S+{x};

N=N-{x}

}

returnS;

}

1) 建立候选集合N。以该集合作为可行解，并从中选出最优解。

2) 创建解集合S。每次进行贪婪选择后都会引起解集合S的扩展，由此获得一个符合度量标准的完整解。

3) 建立解决函数。

4) 建立选择函数。确定贪婪度量的评价标准，分析得到构成问题解的最佳候选对象。

5) 建立可行函数。程序包含以下运行步骤：最初解集合S保持空的状态，根据贪婪度量标准确定选择函数select。

1.2 负荷预测实现

贪婪算法的处理方式是先寻找各阶段最优结果，通过短期处理获得全局最优解。考虑到各阶段只涉及部分信息，单独通过计算机进行处理的贪婪算法有可能会产生最差结果。由此得到经过修改的最优解。

按照以下流程编写贪婪选择程序。

(1) 将原始数据P导入系统中，之后将其分配给任务表[M，N]。

(2) 根据贪婪度量标准select进行任务序列排序，并构建任务候选集合C。

(3) 确定目标函数R，对候选集合N实施贪婪选择，其中，i=1。

(4) 从候选集N内选出具有最高优先级的任务Tk，同时移除k列，构建解集合S,j=i+1。如果j<=N,则跳转至第4步；反之，跳转至第5步。

(5) 当集合S不属于问题的解时，TR=Tmax，再判断将TR加入集合S内是否符合可行性条件。

(6) 将解集合S输出。

2 结果分析

选择某市3片区中的5个街区作为分析对象，先将原始数据导入系统中，再按照下述步骤进行处理。

进行贪婪选择的具体过程，如表1所示。

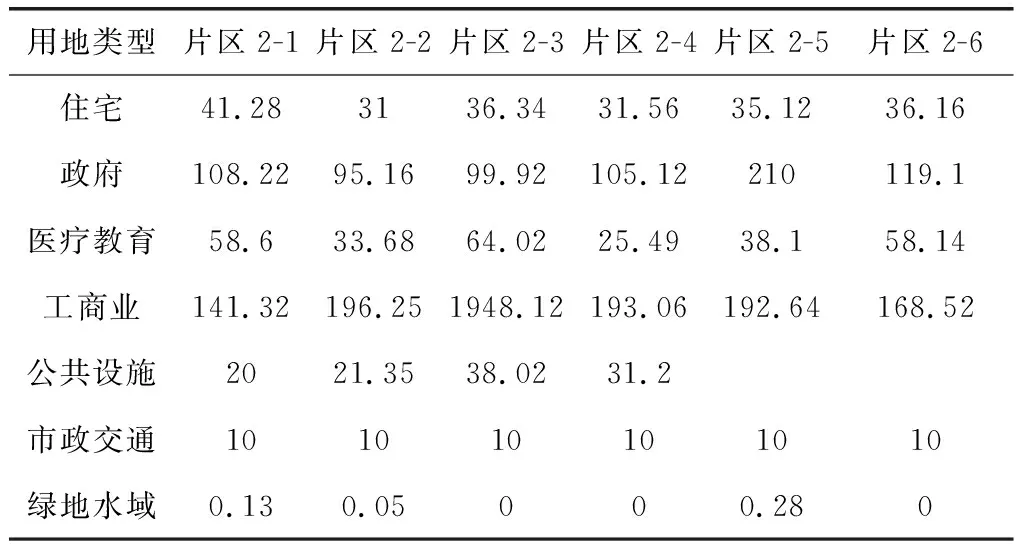
表1 贪婪选择过程

1) 先找到具有相同数值的负荷密度数据。再将这些数据都标记成绿色，使其成为常数，确保其被排除在未来决策之外，以此作为最优负荷密度。

2) 对剩余数据按照显著性高低顺序进行排列，具有一致显著性的数据可选择任意方式进行排列。

3) 从队列第一个数据开始，直至最后完成全部数值的检查或直到最后一个无红色标记的数值。以最后一个或多个未标记红色的结果作为最优选择。

本文对改进算法优越性进行了验证，依次选择单一网格法与利用贪婪算法进行改进后的网格法来预测各片区的负荷情况，同时计算得到二个算法的误差比例。对1片区与2片区进行分析可以得到，如图2所示。

其中，黑色实线是以单一网格法对负荷进行预测得到的误差比例，蓝色虚线代表通过贪婪算法改进后得到的网格法负荷预测差异性，最后将上述预测结果通过不同的图形进行表示。

对4个片区采用两种不同算法进行分析得到的误差比例可以发现，对7类负荷密度利用贪婪算法改进后实现了误差的明显下降。误差校正的结果显示，住宅具备为99%，政府为34%，工商业为98%，教育医疗为78%，公共设施为100%。之后对上述各片区用地误差实施横向对比后发现误差发生降低。

图2 片区误差比例

为更加深入采用分析贪婪算法改善网格法误差的效果，依次从住宅、教育医疗、政府、工商业不同用地种类方面对比了各片区误差。对典型区各类用地负荷进行预测的误差情况，如图3所示。

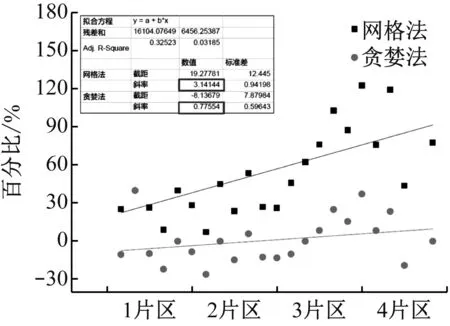
图3 住宅负荷预测误差结果

当拟合曲线与百分比等于0的水平线接近时，说明预测误差很低。经测试发现采用贪婪法进行拟合可以得到更接近0的斜率。

以贪婪法改进得到的负荷预测结果除了具备更低的误差以外，并可以有效压缩数据的处理量。并且随着负荷预测范围的增大，还可以获得更优的效果。通过综合运用网格法与贪婪算法，可同时实现提升负荷预测速率与减少数据处理量的效果。

3 总结

对7类负荷密度利用贪婪算法改进后实现了误差的明显下降。误差校正的结果显示，住宅具备为99%，政府为34%，工商业为98%，教育医疗为78%，公共设施为100%。各片区用地误差实施横向对比后发现误差发生降低。

当拟合曲线与百分比等于0的水平线接近时，说明预测误差很低。经测试发现采用贪婪法进行拟合可以得到更接近0的斜率。并且随着负荷预测范围的增大，还可以获得更优的效果。通过综合运用网格法与贪婪算法，可同时实现提升负荷预测速率与减少数据处理量的效果。