基于混合模型的内容资源流行度预测算法

方元武, 何雪

(1.中国移动通信集团广东有限公司, 广东 广州 510627; 2.广州丰石科技有限公司, 广东 广州 510650)

0 引言

随着互联网内容井喷式上架和爆发式增长，对网络服务商的服务器资源和网络带宽提出了更高的要求，内容的缓存命中率也极大影响着用户的体验[1]。如何在有限的条件下更合理地进行内容缓存是网络服务面临的主要问题，解决此问题的关键是需要一套科学决策方法对内容资源的流行度进行精准预测。精准的流行度预测不仅在用户体验上预知用户行为，降低访问时延，也能在网络安全方面提前部署，减少因拥塞等问题导致的网络溢出[2]。

预测领域经过多年的研究，已经在视频[3]、社交[4]、新闻[5]、民生[6]、旅游[7]等多个行业应用，起到了很好的预测效果和指导作用，但是随着社交互联网的持续演进，现有研究对不同情况的预测却稍显不足。文献[8]提出基于累计访问次数方差的相关性构建时间序列模型，优于现有的流行度预测，但缺少考虑社交网络行为带来的话题影响，参数维度不足；文献[9]提出基于logistic机器学习算法计算用户行为信息，适用于消费数据稀疏的案例，对于长历史数据缺乏参考意义；文献[10]提出新型混合多回归模型预测视频流行度，该模型使用浏览时间和分享次数作为预测变量，考虑了用户网络行为，优于其他线性回归模型，然而对时间序列样本较多的数据，预测效果欠佳。

本文结合已有研究，以社交网络数据为基础，提出一种不限历史数据长短的内容资源的流行度预测算法。分别针对历史数据稀疏的资源和长历史特征数据的资源采用线性回归算法和ARIMA时间序列算法。对比传统的流行度预测，这种混合的流行度预测算法，既适应稀疏数据的局部性特征也能适应长历史数据的季节性变化特征，表现出更高的预测精度。

1 流行度预测算法

1.1 算法流程介绍

流行度是度量内容资源热度的重要指标之一。对流行度的预测，机器学习是运用的较多的一种方法，然而机器学习通常需要基于大量样本进行模型训练，以提高预测精度[11]。对于上新或者数据周期短的内容资源，机器学习算法预测效果明显失真[12]。为了适应不同情况的内容资源预测，实验采用基于线性的多元回归和基于时间序列的ARIMA模型结合的混合预测模型。多元回归预测适用于数据稀疏的内容资源，ARIMA算法适用于样本数据较大并且具备季节性周期的数据。这种混合模型通过互补的方式，提高了预测的包容性，能够在变化的环境中保证一定的预测精度，如图1所示。

图1 内容资源的流行度预测模型算法流程

1.2 基于多元回归的流行度预测算法

数据稀疏内容资源呈现出历史数据的局部性、相邻时间记录的强相关性的特点，正好与多元回归算法切合[13]。基于内容资源流行度的多元线性回归预测算法，如式(1)。

(1)

式(1)利用最近t-1(t<=7)天的流行度预测第t天的流行度，Y(t)即为预测结果。Ni为内容资源在第i天流行指数(见公式(1))，βi为第i天的权重，εt(t=1,2,…,n)是随机项误差，α是常数，n为天数。

受社交网络的影响，内容资源的流行程度不一，对于突发性的内容可能经过前期潜伏之后，后期呈指数级别上升，前后产生巨大的差距，容易因预测计算溢出导致结果失真。应对这种情况，可以在线性回归的基础上进行对数处理，然后基于对数结果预测内容资源流行度。这样的做法在保持原数据单调性的同时，也能弱化数据变化的敏感度。通过多元指数线性变换和对数变换建立多元对数回归模型。

多元指数线性回归模型，如式(2)。

(2)

对数变换公式，如式(3)。

(3)

1.3 基于ARIMA的流行度预测算法

ARIMA[14]模型是一种只考虑数据内在联系的时间序列算法，更适用于长历史特征的数据分析。ARIMA包含3个部分，AR代表的自回归模型(Autoregression)；I代表的差分运算(Intergrated)；MA代表的移动平均模型(Moving Average)。自回归项p，差分阶数d，移动平均项数q分别是自回归模型、差分运算和移动平均模型的参数[15]，取值皆为非负整数，用ARIMA(p,d,q)表示。

经过差分处理使序列趋于平稳化后的ARIMA(p,d,q)模型表示，如式(4)。

(4)

式中，{Ni-p,…,Ni-2,Ni-1,Ni}表示该时间序列数据；B表示延迟算子；{εi-q,…,εi-2,εi-1,εi}表示随机干扰序列；{φ1,φ2,…,φp}、{θ1,θ2,…,θq}分别表示自回归系数和移动平均系数；d=(1-B)d表示d阶差分；S表示季节周期。

2 实验

2.1 数据收集

本文通过编写爬虫程序，爬取了Alexa网站、中国站长站、微博等网站，收集包括访问量、浏览量、搜索指数、话题热度等数据。为了使数据更加易于处理，剔除了访问量、浏览量小于100的资源，最后剩余8 304个样本资源。

2.2 数据准备

社交互联网的新时代，单纯以访问量、流量评估流行度已不足以满足对内容资源的评价，话题次数、搜索次数也对资源流行程度产生重要影响。因此，结合网络行为特征，选取访问量、浏览量(PV)、搜索指数、话题热度为参数对资源的流行度进行评价，如式(5)。

Ni=w1(v,i)+w2(p,i)+w3(s,i)+w4(t,i)

(5)

式中，Ni是第i个资源的流行指数，w1,w2,w3,w4分别是访问量、PV、搜索指数及话题热度对流行指数的影响系数。

经过流行指数评价标记，得到所有样本资源每天的流行度指数，流行度d值越大代表资源的网络流程程度越高。样本数据，如表1所示。

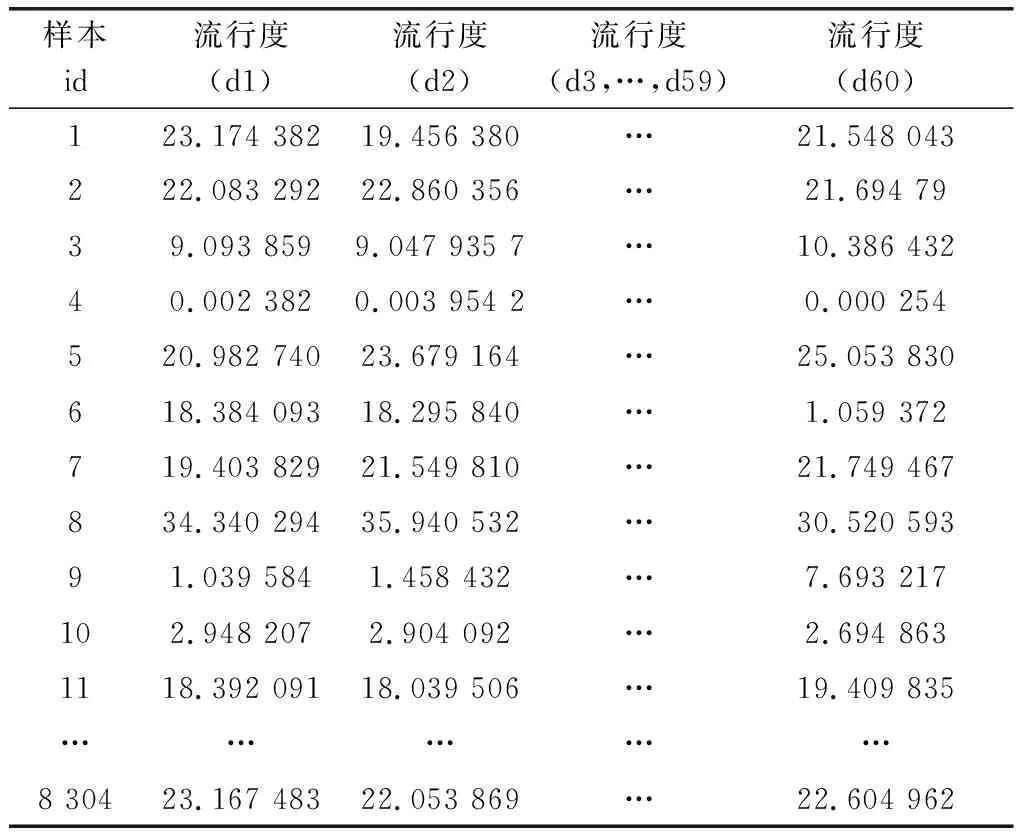
表1 内容资源流行度样本数据

2.3 数据建模

根据图1的算法流程，按照数据是否低于7天将上述数据拆分为的稀疏资源和长历史特征资源，分别对其进行线性对数回归模型构建和ARIMA模型构建。

1.多元对数回归模型构建

数据范围在一周内的数据样本共23个，将23个样本数据按照线性模型方程进行线性指数求和，然后对指数和进行对数变化，得到方程的解，如图2所示。

图2 多元对数回归计算结果

如图2，(1) 判定系数R2=0.958 513，接近1，说明稀疏数据资源第t天与第t-1,t-2,…，1天的流行度存在强相关性，拟合程度较高[16]。

(2) 统计量F=341.502 2，若取显著性水平α=0.05，由F分布表查询临界值F0.05(6,15)=2.79<341.502 2，表示y(t)与N1,N2,…,Nt之间不存在显著差异，即存在相关性。

2.ARIMA模型构建

步骤一：序列平稳化，差分定阶。按照算法流程将一周以上的样本数据进行时间序列呈现。逐步对时间序列进行阶数的差分处理使序列平稳；经过二阶差分，单位根(ADF)检验序列得到统计值为-7.231，落在1%的置信区间，概率小于0.05，因此确定差分阶数d=2。

步骤二：参数估计。利用Eviews软件计算得到平稳序列后的自相关图和偏相关图，如图3所示。

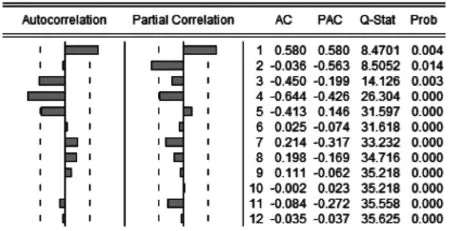
图3 序列差分后的ACF图和PACF图

自相关系数在滞后4阶的时候落在2倍标准差的边缘，PACF呈二阶拖尾，因此q可以考虑取1或4，p可以取1或2，对模型进行检验，如表2所示。

表2 模型检验结果

参数(2,1)的AIC和SC检验参数最理想，确定模型为ARIMA(2,2,1)。

步骤三：模型适应性检验。检查模型的残差是否相关，平均分布是否为0。因此，获取计算结果的值进行模型诊断，如图4所示。

(a)

(b)

图4(a)时间序列中，残差没有明显的周期性变化；图4(b)对残差进行差分计算，发现时间序列残差与其本身的滞后版本没有明显的自相关性。综上，判断残差为白噪声。实验构建的ARIMA(2,2,1)模型对长周期序列的内容资源流行度预测是合适的。

2.4 模型预测

将上述已确定参数的多元对数回归模型和ARIMA模型组合为混合模型，并输入历史数据，利用混合模型预测未来流行度指数。模型预测情况，如图5所示。

图5 混合模型内容流行度预测情况

由图可知预测值与实际值高度重合。

2.5 MAE模型性能评估

采用MAE(平均绝对误差)方法评估混合模型实际预测误差，如式(6)。

(6)

实验分别对文章提出的混合模型(mixture)与其他文献中提到的基于线性回归模型预测方法(linear-model)、基于对数回归模型预测方法(log-model)以及基于ARIMA模型的预测方法进行对比，如图6所示。

图6 预测绝对误差率对比结果

由图可知，实验中的混合预测方法的预测绝对误差率低于0.38%，误差率最小。

3 总结

为实现对不同历史数据周期内容资源的流行度预测，本文结合多种统计学方法，在对基础数据预处理后，分别对短周期资源和长周期资源进行多元对数回归算法流行度预测和ARIMA时间序列算法流行度预测。经过误差分析和对比后，得到的混合模型绝对误差率在0.38%以下，优于其他模型方案。该模型可以基于历史数据，为互联网服务商在资源缓存方面提前规划提供指导，提前布局。在结合实际应用的过程中，可以扩大样本数据范围，利用现代科技的大数据处理能力和人工智能技术，挖掘更多特征信息，提升数据的科学决策能力。