基于关联规则挖掘算法Apriori的土木工程课程相关性分析*
2020-12-24黄川腾蒲爽唐迪李青
黄川腾 蒲爽 唐迪 李青

摘 要:人才培养方案是专业教育的总体设计与规划,对保证人才培养质量具有决定性作用。人才培养方案包含的培养目标、毕业要求、课程设置、教学大纲和评价体系有严密的逻辑关系,课程设置和课程结构是人才培养方案落地的具体抓手。土木工程课程中的专业教育类课程包括数学课程群、力学课程群和设计课程群,文章选取各课程群中的代表性课程共计7门,以三个年级249名学生学习成绩为研究对象,使用关联规则挖掘算法Apriori,深入探讨数据挖掘技术的实现过程,明确课程间关联关系的强弱。分析结果可为课程体系设置与结构调整、课程体系重难点课程精准控制、教学方法改革和学情监控与预测提供重要参考。
关键词:关联规则; Apriori;土木工程;课程;相关性分析
中图分类号:G642 文献标志码:A 文章编号:1673-8454(2020)23-0055-05
一、引言
根据高校定位,培养符合行业和社会需求的人才,根本在于制定理念和思路清晰的专业人才培养方案。完整的人才培养方案应包括培养目标、毕业要求、课程体系、教学大纲和评价体系等五方面的内容,从宏观到微观具有严密的逻辑关系,其中课程体系承上启下,既是对培养目标和毕业要求的具体支撑又是对教学大纲和评价体系的明确引导。纵观各高校土木工程专业课程体系,均包含通识与素质类、公共基础类及工程素质类课程。基于工学学科特点,公共基础类中的数学课程群课程、工程素质类中的力学课程群课程和设计课程群课程,在土木工程专业课程体系中都是本科各阶段的核心课程,这些课程也是支撑土木工程专业素养的骨架,对学生专业素养培养目标的达成具有决定性意义。
本文从数学课程群中选取高数(上)、高数(下)、线性代数,从力学课程群中选取理论力学、材料力学、结构力学,从设计课程群中选取混凝土结构设计原理共7门课作为研究对象。课程选取原则有三:其一,具有代表性。选取的课程均是课程群核心课程,同时也是硕士研究生入学考试课程,或者是考研复试的核心课程。其二,覆盖面广。所选课程开课时间有先后关系且涵盖大一到大三,对课程的考察能够反映学生在大学期间的学习行为习惯,分析结果能够用于指导人才培养方案修订及学情监控与预测。其三,课程具备相关性分析的基础前提,相关性分析结论具备指导意义。土木工程专业中,数学课程是力学课程的基础,力学课程直接指导设计课程,各课程群课程内容前后均有关联。
本文选取土木工程专业7门核心课程,以三个年级249名学生学习成绩为研究对象,使用关联规则挖掘算法Apriori,深入探讨数据挖掘技术的实现过程,发掘课程间的强弱关联关系。分析结果可为课程体系设置与结构调整、课程体系重难点课程精准控制、教学方法改革和学生学情监控与预测提供参考。
二、研究方法
课程相关性分析用于描述课程之间的关联程度。目前课程相关性分析研究所采用的方法多以數据挖掘技术为基础,主要有相关分析法、典型相关分析法和关联规则分析法。[1]其中尤以Apriori算法为代表的关联规则分析法应用最广,关联规则挖掘就是在交易数据、关系数据或其他信息载体中查找存在于项目集合或对象集合之间的频繁模式、关联、相关性或因果结构。[2]关联挖掘是一种简单、实用的分析技术,是发现存在于大量数据集中的关联性或相关性,从而描述一个事物中某些属性同时出现的规律和模式。
1.基于关联规则挖掘的Apriori算法
关联规则挖掘的数据集记为D(一般为事务数据库),D={t1,t2,…,tk,…,tn},tk={i1,i2,…,im,…,ip},tk(k=1,2,…,n)称为事务(Transaction),im(m=1,2,…,p)称为项(Item)。设I={i1,i2,…,im}是D中全体项组成的集合,I的任何子集X称为D中的项集(Itemset),若X中有k项,则称集合X为k项集(k-Itemset)。数据集D中包含项集X的事务数目称为项集X的支持数,记为?滓x。项集X的支持度记为support(X)。
support(X)=■×100%(1)
式(1)中|D|是数据集D的事务数。
若X、Y为项集,且X∩Y非空,X→Y称为关联规则,X、Y分别称为关联规则X→Y的前提和结论。关联规则X→Y的支持度,记作support(X→Y)。
support(X→Y)=support(X∪Y)(2)
关联规则X→Y的置信度记作confidence(X→Y)。
confidence(X→Y)=■×100%(3)
支持度描述了X和Y这两个项目集合的并集在所有的事务记录中出现的概率有多大。支持度和置信度可以比较直接地形容关联规则的性质。置信度是对关联规则正确率的衡量,支持度是对关联规则重要性的衡量。支持度说明了这条规则在所有事务中有多大的代表性,显然支持度越大,关联规则越重要。有些关联规则的置信度虽然很高,但支持度却很低,说明该关联规则实用的机会很小,因此不重要。[2]鉴于事务数有限,多项集关系支持度过低,加之课程间二项集关系最具逻辑关系及指导意义,本文仅考察课程二项集相关关系。
2.数据处理
本文将基于学生各科成绩进行课程相关性分析,滤除缺考、缓考、免考、违纪等情况,将2014-2016级249名学生的7门课程成绩记为数据集D,共包含249条事务,每条事务tk为7项集。
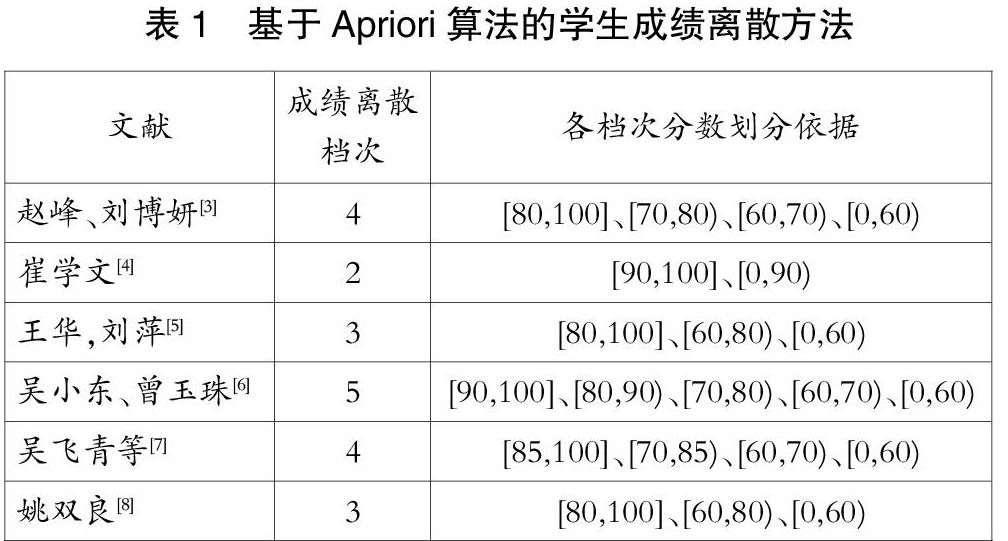
表1展示了各学者利用Apriori算法进行相关性分析前对学生成绩进行离散化处理的方法。上述学者均选用了课程综合成绩作为离散对象,且均采用按分数分段离散的方法。
由于大学课程综合成绩是由形成性考核(作业、考勤、课堂表现等)与终结性考核(期末考试)按一定比例共同组成的。江辉等[9]分析发现大多数课程的终结性考核成绩与形成性考核成绩不存在显著线性相关关系。换句话讲,因为形成性考核的加成,综合成绩并不能直接反映学生对课程知识的掌握程度。容易理解,一方面,形成性考核针对过程管理,重在考察学生对学习的态度和投入度,而学生为拉升综合成绩可能会通过其他手段(作业网络搜索、抄袭,请人签到等)提高平时成绩分值;另一方面,任课教师为了综合成绩分布更合理,可能会人为调整各层次学生形成性考核成绩。尤其是对于学困生,形成性考核成绩对综合成绩的提升会非常显著。为了直观衡量学生知识能力水平,本文选用终结性考核(期末考试)卷面成绩作为离散考察对象。
此外,由于不同科目、不同年级、不同任课教师在试卷出题难度、批阅习惯上均有很大不同,往往造成各课程成绩均值和方差差异巨大,甚至某些课程成绩不符合正态分布。因此,不能单纯以“分数论高低、分优劣”。针对同一科目,本文对同一班级全体学生终结性考核(期末考试)卷面成绩取四分位数,排序后前25%为优秀、中上25%为良、中下25%为中、末尾25%为差。分别用1、2、3、4表示。
最后,为方便描述,将高数(上)、高数(下)、线性代数、理论力学、材料力学、结构力学和混凝土结构设计原理7门课分别以字母A、B、C、D、E、F、G表示。例如,某学生材料力学成绩排在全班前25%,则该生成绩经过数据处理后表示為E1。
三、挖掘结果
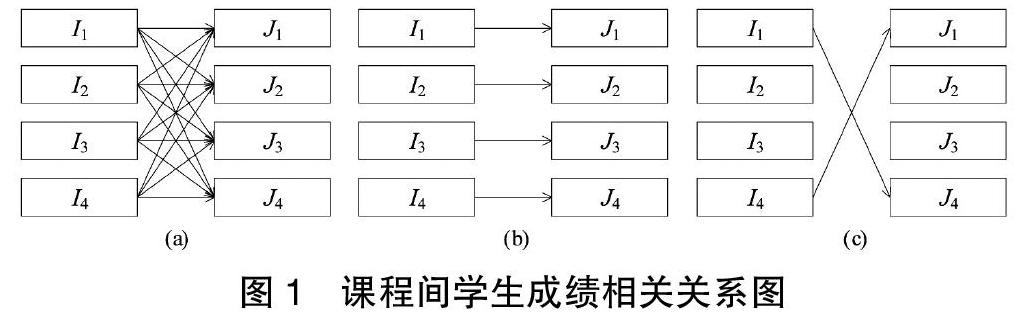
任意两门课I、J,课程I开课早于课程J,如图1(a)所示,两门课的学生成绩先后关系一共有16种,例如,I2→J4表示在课程I中成绩为良、在课程J中成绩为差。图1(b)所示关系(In→Jn),表示课程间成绩的延续性或者惯性,意味着在前后两门课中学生取得相同等次的成绩。图1(c)所示关系(I1→J4或I4→J1),表示课程间成绩的反转性,意味着在前后两门课中学生取得完全相反等次的成绩。理论上说,两门课联系越紧密,知识点延续性越强,课程相关性越高,同一名学生考试成绩的惯性越强、反转的可能性越低,反之亦然。为了衡量学生课程成绩的惯性和反转性,定义惯性指数和反转指数如下。
Kin=■support(I1→Ji)(4)
Kre=support(I1→J4)+support(I4→J1)(5)
表2完整地展示了本文所选7门核心课程之间的关联分析结果。图2展示了7门核心课程之间的反转指数和惯性指数。
四、结果分析
根据本校人才培养方案,本文所选土木工程专业7门核心课程,具有一致的先后关系,涵盖大一至大三。从表2中的关联分析结果和图2中的反转指数及惯性指数可以发现以下一些现象和规律。
(1)核心课程之间存在较为显著的成绩等级固化现象。成绩等级固化普遍存在于本文所选7门核心课程之间,证明了土木工程专业数学课程群、力学课程群以及设计课程群课程紧密的关联性。固化现象尤其存在于优生和差生群体,各门课之间“优”和“差”两个等次置信度几乎都在40%以上,其中confmax=conf(F4→G4)=65.1%, confmin=conf(A4→F4)=39.4%。尽管“良”和“中”两个等次的支持度和置信度均小于“优”和“差”,但若将“良”和“中”合并,将“优良中差”四级评判变为“优中差”三级评判,一个有趣的现象是,三级评判的“中”等次,以“高数(上)→高数(下)”为例,support(A中→B中)=31.3%,conf(A中→B中)=63.4%,说明成绩中等的学生在“良”和“中”这两个层级范围内流动性非常大,反映出这部分学生的学习效果对课程特点、教学方法甚至教师个人魅力的敏感度最高。
(2)课程群内课程相关性显著高于课程群间课程,力学课程与设计课程相关性显著高于数学课程与力学课程相关性。如表2所示,尽管总体上7门核心课程成绩等级固化现象很明显,其一体现在成绩等级惯性的置信度较高,其二也表现在成绩等级反转(1→4,4→1)的支持度和置信度都非常低。但固化趋势在课程群之间课程与课程群内课程仍存在不同。图2完整展示了7门核心课程之间学生成绩的反转指数Kre及惯性指数Kin,图3展示了反转指数Kre及惯性指数Kin序列图。反转指数越低、惯性指数越高,可以认为课程关联性越强。如图所示,课程群内课程、力学课程与设计课程表现出显著的强关联特征。其中一个非常有趣的现象是,结构力学与设计课程(F→G)的关联性显著高于其他课程,同时,数学课程对结构力学的影响显著低于对理论力学和材料力学的影响,这充分反映出结构力学课程独特的特征,这种现象可以解释为结构力学对杆系结构内力、变形的求解对设计课程的重要性,但求解过程并不需要深入的数学知识(实质上,静定结构力学与超静定结构力学部分运算难度确实只限于四则运算)。
(3)数学课程群和力学课程群的抓手分别是高数(上)和材料力学。从表2中可知,数学课程群中,“高数(上)→高数(下)”以及“高数(上)→线性代数”在各等次成绩(In→Jn)的置信度中较“高数(下)→线性代数”占有优势;类似地,在力学课程群中,“材料力学→结构力学”在各等次成绩(In→Jn)的置信度中较“理论力学→材料力学”和“理论力学→结构力学”占有优势。此外,从图3中反转指数和惯性指数可知,“高数(上)→高数(下)”以及“材料力学→结构力学”的关联性在数学课程群以及力学课程群中是最高的。最后,从课程教学内容上,高数(上)着力构建一元函数微积分学,高数(下)进一步把一元函数微积分学推广到多元函数微积分学上。[10-12]材料力学以杆件为对象结合截面应力分布重点讲解了计算简图、弯矩、剪力、轴力、变形等知识点,结构力学以杆系结构为对象进一步拓展和强化了结构内力(弯矩、剪力、轴力)和变形的计算方法。因此对于高数(上)与高数(下)、材料力学与结构力学,后者知识体系是前者的传承和推广。
五、结语
本文在土木工程专业数学课程群、力学课程群和设计课程群中选择了7门代表性课程,以三个年级249名学生学习成绩为研究对象,使用关联规则挖掘算法Apriori,深入探讨数据挖掘技术的实现过程,提出了课程成绩惯性及反转的概念,构建了惯性指数和反转指数,结合课程间的支持度和置信度,发掘了课程间的关联关系。得到了核心课程之间存在较为显著的成绩等级固化现象、课程群内课程相关性显著高于课程群间课程、力学课程与设计课程相关性显著高于数学课程与力学课程相关性、数学课程群和力学课程群的抓手分别是高数(上)和材料力学等结论。分析结果可为科学进行课程体系设置与结构调整、准确把控课程体系中的核心课程、有的放矢地进行教学方法改革、学情监控与预测提供重要参考,也是笔者利用大数据算法进行教学研究的积极探索。
参考文献:
[1]宋小敏,张国防,邢淑兰,汪锁田.基于数据挖掘的课程相关性分析方法[J].山西财经大学学报,2012(S3):240,257.
[2]朱明编.数据挖掘导论[M].合肥:中国科学技术大学出版社,2011:102.
[3]赵峰,刘博妍.基于改进Apriori算法的大学生成绩关联分析[J].齐齐哈尔大学学报(自然科学版),2018(1):11-15.
[4]崔学文.关联规则挖掘算法Apriori在学生成绩分析中的应用[J].河北北方学院学报(自然科学版),2011(1):44-47.
[5]王华,刘萍.改进的关联规则算法在学生成绩预警中的应用[J].计算机工程与设计, 2015(3):679-682,752.
[6]吴小东,曾玉珠.基于Apriori算法的高校学生成绩数据挖掘[J].廊坊师范学院学报(自然科学版),2019(1):31-36.
[7]吴飞青,吴成玉,方伟,孙炯,王媛媛.基于数据挖掘的成绩相关性实证分析[J].电气电子教学学报,2019(4):1-4.
[8]姚双良.数据挖掘在高校课程相关性中的应用研究[J].科技通报,2012(12):232-234.
[9]江辉,周凌,叶雪飞.形成性与终结性考核成绩相关关系分析[J].中国远程教育, 2011(8):58-62.
[10]同济大学数学系编.高等数学(第七版)(上、下册)[M].北京:高等教育出版社,2014.
[11]孙训方,方孝淑,关来泰编.材料力学1(第五版)[M].北京:高等教育出版社,2009.
[12]萧允徽,张来仪主编.结构力学(I)(第3版)[M].北京:机械工业出版社,2018.
(编辑:王天鹏)
