关于《数据结构》（C语言版）构造赫夫曼树的思考

方利胜

摘  要：目前构造赫夫曼树的方法有时会出现两种情况，而赫夫曼树又称“最优二叉树”，因此应该是唯一的。文章通过比较两种赫夫曼树所生成的赫夫曼编码，阐述了两种赫夫曼树何种最优，从而实现了对现有构造赫夫曼树方法的补充和完善。

关键词：赫夫曼树;赫夫曼编码;最优二叉树;数据结构

中图分类号：TP311 文献标志码：A         文章编号：2095-2945（2020）26-0065-03

Abstract： At present， there are sometimes two ways to construct Huffman Tree， and Huffman Tree is also called “Optimal Binary Tree”， so it should be unique. In this paper， by comparing the Huffman Codes generated by the two Huffman Trees， the best of the two Huffman Trees is explained， thus realizing the supplement and perfection of the existing method of constructing Huffman Trees.

Keywords： Huffman Tree; Huffman Code; optimal binary tree; data structure

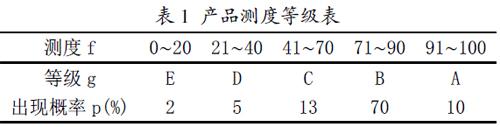
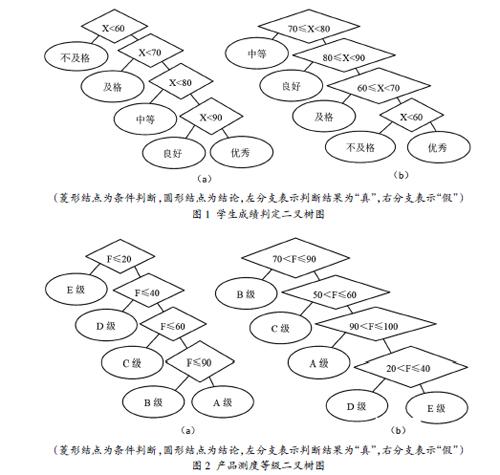
在实际生活中，我们常常会遇到考察最佳判断的问题，例如在考察课记分时，往往把百分制转换成优（x≥90）、良（80

又如设某工厂的某种产品按某种测度分等级，如表1所示：

表1 产品测度等级表

其中，表中“出现概率”是指对应等级的产品的出现概率。图2中给出了对应两种不同判定方式的二叉树。表面看，似乎图2（a）对应的判定方式效率高（每个判定式都是简单的“小于等于”判断），但分析每种等级的出现概率，E级只有2%，在实际中极少出现，而B级出现概率最大，在图2（b）的判定方式中，一次“命中”的机会很大，余下的分支很少需要判断，因此，图2（b）的判定方式应该效率最高[2]。

事实上，以上两个问题均可利用构造赫夫曼树的方法进行解决。问题一中，假设学生成绩对于不及格、及格、中等、良好和优秀的分布概率分别为5%，15%，40%，30%，10%，以它们作为叶子的权值来构造赫夫曼树，如图1（b）所示，它可以是大部分的分数值经过较少的比较次数得到相应的等级。

而在第二个问题中，因为不同的判别方式，对应不同的二叉树，若把等级出现概率看作叶子的权值，则图2（b）判定方式的选择，实际上就是构造赫夫曼树的问题。

赫夫曼树，又称最优二叉树，是一类带权路径长度最短的树。首先给出路径和路径长度的概念，从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度，树的路径长度是从树根到每一个结点的路径长度之和，结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积，树的带权路径长度为树中所有叶子结点的带权路径之和，通常记作WPL=∑  wklk，假设有n个权值{w1，w2，……wn}，试构造一颗有n个叶子结点的二叉树，每个叶子结点带权为wi，则其中带权路径长度WPL最小的二叉树称做最优二叉树或赫夫曼树[3]。

赫夫曼树除了用于最佳判断，还可用于构造赫夫曼编码。在实际编码时，将每个字符出现的频率作为叶子结点的权赋予该结点，求出此树的最小带权路径就是传送电文的最短长度，因此，编码问题就转换成了设计赫夫曼树的问题。在编码时，对与给定的字符集C={c1，c2，…cn}及字符出现的频率W={w1，w2，…wn}，以c1，c2，…cn作为叶结点，以 w1，w2，…wn作为该结点上的权构造赫夫曼树，对赫夫曼树中每个分支结点的左、右分支分别用0和1进行编码，这样从树的根结点到每个叶结点之间，沿途路径上的0和1组成编码序列就是叶结点所代表字符的二进制编码，赫夫曼编码使电文的总长度最短。由于树中没有一片树叶是另一片树叶的祖先，而字符集中每个字符都在叶结点上，每个叶结点对应的编码不可能是另外一个叶结点的前缀码，即利用赫夫曼树得到的字符编码是最优的前缀编码[4]。

对于赫夫曼树的构造方法，目前的教科书中主要有两种，第一种构造方法叙述为：（1）根据给定的n个权值{w1，w2，……wn}构成n个二叉树的集合F={T1，T2，……Tn}，其中每棵二叉树Ti中只有一个带权为wi的根结点，其左右子树为空。（2）在F中选取两棵根结点的权值最小的树作为左右子树构造一颗新的二叉树，且置新的二叉树的根结点的权值为其左右子树上的根结点的权值之和。（3）在F中删除这两棵树，同时将新得到的二叉树加入F中。（4）重复（2）（3），直到F只含一棵树为止。这棵树便是赫夫曼树[3]。

第二种方法叙述为：（1）根据给定的n个权值w1，w2，……wn构成n个二叉树的森林F={T1，T2，……Tn}，其中每棵二叉树Ti中只有一个权值为wi的根结点，没有左右子樹。（2）在森林F中选出两棵根结点权值最小的树（当这样的树不止两棵时，可以从中任选两棵），将这两棵树合并成一棵新的二叉树。这时会增加一个新的根结点，它的权值为原来两棵树的根的权值之和，而原来的两棵树就作为它的左右子树。（3）对新的森林F重复（2），直到森林F中只剩下一棵树为止。这棵树便是赫夫曼树[5]。

不难看出，二者的区别是第二种方法在第（2）步选择两个根结点权值最小的树时提到了这样的树可能不止两棵的特殊情况，而其提出的解决方法是从中任选两棵。那么，在实际构造赫夫曼树时，是否会出现第二种构造方法所提到的特殊情况呢？如果会，那么按照任选两棵的解决方法又是否会对最终的结果产生影响呢？下面我们就通过事例来进行说明。

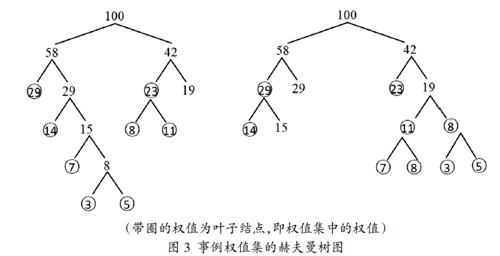
按第一种构造方法对权值集w={5，29，7，8，14，23，3，11}进行赫夫曼树构造，结果可以构造出两种赫夫曼树，经验证，两者的带权路径长度之和WPL相等且为最小，这说明出现了第二种构造方法所提到的特殊情况（两种赫夫曼树如图3所示）。

经分析，产生两种赫夫曼树的原因在于构树过程中，新生成的二叉树的根结点的权值与F中某一棵二叉树根结点的权值相等，假设令该权值为m，为加以区分，新生成的m定义为m'，F中该权值定义为 ，m'= ，在生成m'后，再进行构树时，可以选择与m'或 中的任意一个结合，在本例中，m为8，在3和5生成8，即为8'后，再进行构树时，7既可以与8'结合，也可以与F中的8（即 ）结合，因此出现了两种赫夫曼树。

既然出现了特殊情况，那么任选两棵的解决方法是否会对最终结果产生影响，即是否生成的两棵赫夫曼树的最优化程度相同呢？

赫夫曼树又称为“最优二叉树”，而现在赫夫曼树又有两种，那么这两种赫夫曼树都是最优的，还是其中的某一种更优于另外一种呢？考虑到构造赫夫曼树的最终目的是要进行赫夫曼编码，所以可以从最终编码的优劣这一角度出发，得出这个问题的答案。我们把先与m'结合构成的赫夫曼树称为第一种赫夫曼树，把先于 结合构成的赫夫曼树称为第二种赫夫曼树，则在例题中，第一种赫夫曼树的赫夫曼编码为：3-01110，5-01111，7-0110，8-110，11-111，14-010，23-10，29-00，第二种赫夫曼树的赫夫曼编码为：3-0110，5-0111，7-1110，8-1111，11-010，14-110，23-00，29-10。

为了更直观的比较两种编码，引入“码字长度”的概念，规定从树根到每一个叶子结点的路径长度称为“码字长度”。例如，在第一种赫夫曼树中权值3的码字长度为5，在第二种赫夫曼树中权值3的码字长度为4。综上所述，第一种赫夫曼树编码的码字长度和为27，第二种赫夫曼树编码的码字长度和为26，显然在进行编码时，第二种赫夫曼树要优于第一种，所以第二种赫夫曼树才是真正意义上的“最优二叉树”。

构造赫夫曼树时采用应如何选择，《数据结构》（C语言版）中给出的解决方法是在编写程序时构造一个数组，从而保证了构造的赫夫曼树是第二种赫夫曼树。尽管如此，但就赫夫曼树的构造定義而言，《数据结构》（C语言版）中给出的描述，即第一种构造方法是有缺陷的，并且由第二种赫夫曼树优于第一种赫夫曼树这一结果可知，在第二种构造方法中对于特殊情况采用任取两棵的解决方法也是有缺陷的。因此，建议将构树方法作如下修改：（1）根据给定的n个权值{w1，w2，……wn}构成n个二叉树的集合F={T1，T2，……Tn}，其中每棵二叉树Ti中只有一个带权为wi的根结点，其左右子树为空。（2）在F中选取两棵根结点的权值最小的树。（3）将选取的两棵树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上的根结点的权值之和。判断新的二叉树的根结点的权值是否与F中某一二叉树根结点的权值相等，若相等，设该权值为m，为加以区分，令F中对应的该权值为m，若不相等，进入下一步。（4）在F中删除这两棵树，同时将新得到的二叉树加入到F中。（5）重复（2），判断选取的两棵树的根结点的权值中是否包括m，若包括，则这两棵树中必须包括一棵以 为根结点的树，若不包括，则在重复（2）后进入下一步。（6）重复（3）（4），直到F中只含一棵树为止。这棵树便是赫夫曼树。

综上所述，构造出的赫夫曼树就是第二种赫夫曼树，即“最优二叉树”，从而实现了对现有构造赫夫曼树方法的补充和完善。

参考文献：

[1]杨秀金，张红梅.数据结构[M].西安：西安电子科技大学出版社，2004：131.

[2]齐德昱.数据结构与算法[M].北京：清华大学出版社，2003：195.

[3]严蔚敏，吴伟民.数据结构（C语言版）[M].北京：清华大学出版社，1997：144-145，148.

[4]田鲁怀.数据结构[M].北京：电子工业出版社，2006：212.

[5]胡圣荣，周霭如，罗穗萍.数据结构教程与题解（用C/C++描述）[M].北京：北京大学出版社，2003：116.