基于PID参数优化控制的伞钻液压系统仿真分析*
2020-12-24张磊
张 磊
(河南科技职业大学 机电工程学院,河南 周口 466000)
0 引 言
立井开拓作为深层矿井重要施工方式,施工过程复杂,且受地质影响大,施工时间相对总工期占比较高[1]。伞钻作为井筒开凿的重要设备,通过提高其开拓效率,可有效提高立井施工的机械化程度[2]。目前,立井开拓用伞钻控制方式主要为气动和液压两种形式。其中,气动伞钻进尺慢、效率低,因此,液压伞钻的应用相对较为广泛。
传统液压伞钻由手动阀组成液压控制阀组,工作中需手动调节换向阀控制液压缸,通过改变伞钻位姿实现钻孔定位[3]。该方法简单、可靠,但人为因素对定位精度影响较大,且调整时间长,影响施工效率。
为了解决以上问题,笔者设计基于PID参数优化控制的伞钻液压系统,对液压伞钻的机械臂位姿进行控制,以提高立井开拓效率及钻孔定位精度。
1 单臂液压系统分析
笔者以YSJZ4.8全液压四臂伞钻为研究对象,对单组工作臂液压系统进行研究。该伞钻由立柱、大臂、支撑臂、液压系统及凿岩机构成[4],4组钻臂及支撑臂安装于立柱。
伞钻单臂液压系统如图1所示。

图1 伞钻单臂液压系统图
图1中,由于钻臂油缸及大臂油缸对位姿影响较大,笔者对其实施闭环控制;在控制器将钻臂末端位置信息进行计算分析后,将控制信号发送与比例换向阀,通过比例换向阀调节机械臂位姿[5];钻臂及大臂油缸通过磁致伸缩传感器实时采集液压杆位置信息;控制系统的快速响应性及稳定性取决于信号校正,PID控制器通过调节信号,优化系统动态特性。
2 单臂液压系统仿真
AMESim为液压系统仿真分析的重要工具[6]。在系统建模前,笔者作如下假设:
(1)对单臂位姿控制进行建模;
(2)设油液为非压缩性介质;
(3)忽略油液温度变化。
大臂液压缸AMESim仿真模型如图2所示。

图2 大臂液压缸闭环控制系统AMESim仿真模型
仿真模型中各参数为:
液压缸活塞杆及活塞直径分别为40 mm、80 mm;比例换向阀输入电流为100 mA,最大流量为40 L/min;液压泵排量为46.7 L/r,额定转速为1 000 r/min。
PID校正信号为[7]:
(1)
式中:e(t)—活塞杆位移误差信号;u(t)—控制模块校正输出信号;Ti—积分时间常数;kp—比例常数;Td—微分时间常数。
比例、积分、微分常数影响系统整体动态特性,因此,需对以上参数进行整定、优化。
笔者利用AMESim的批处理功能,分别对改变比例、积分、微分常数后液压缸出口压力P变化进行仿真。
比例常数改变时,液压缸的出口压力仿真结果如图3所示。

图3 比例常数改变时液压缸出口压力
积分常数改变时,液压缸的出口压力仿真结果如图4所示。
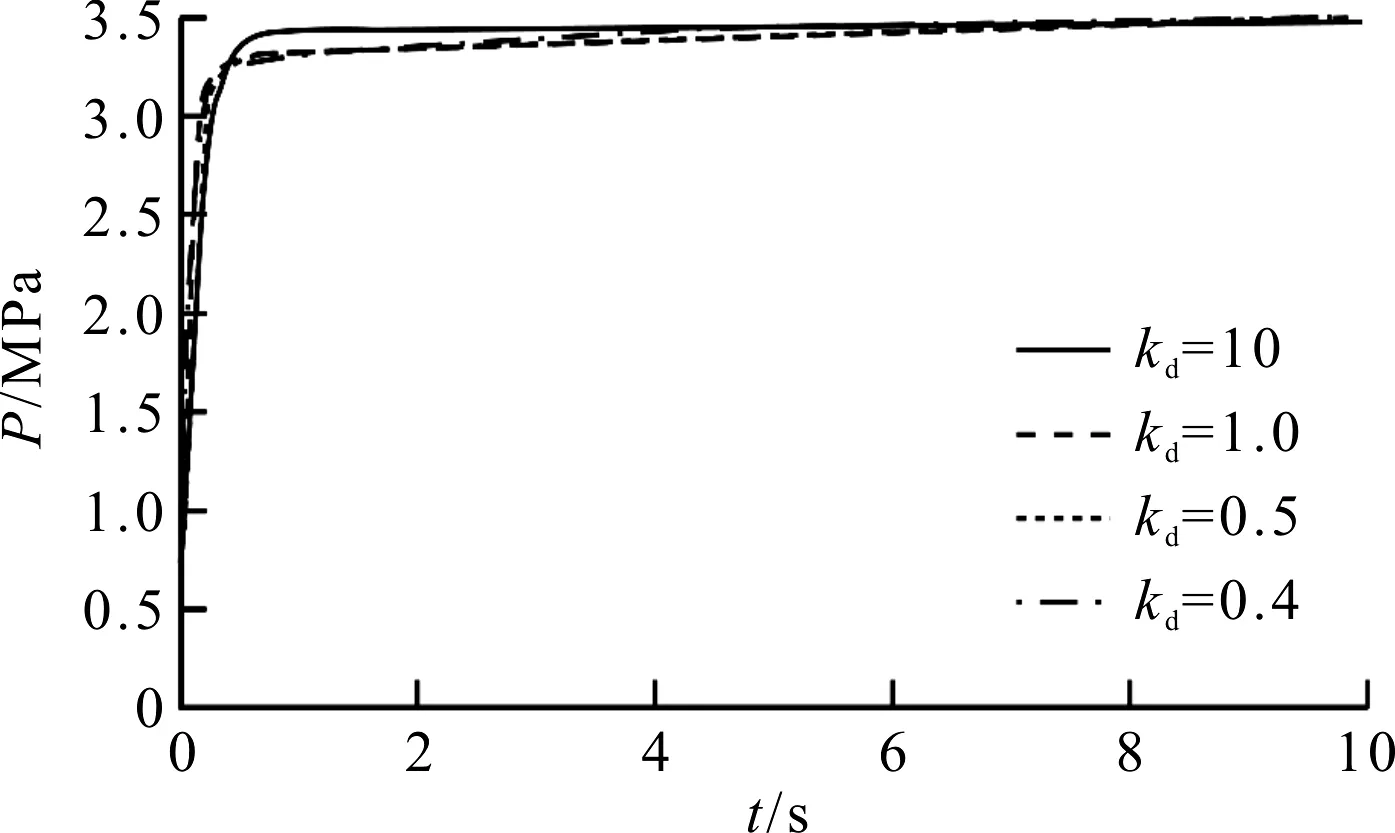
图4 积分常数改变时液压缸出口压力
微分常数改变时,液压缸的出口压力仿真结果如图5所示。
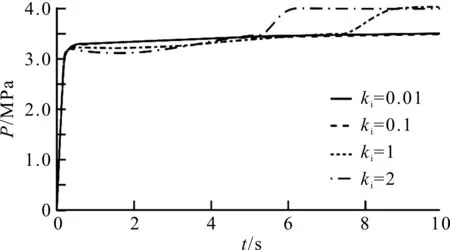
图5 微分常数改变时液压缸出口压力
通过对图(3~5)的仿真分析可知:
(1)针对系统阶跃响应,增大比例常数,系统快速响应性提高,稳态误差降低,但超调量增大;(2)增大积分常数时,稳态误差降低,但动态响应性及稳定性降低;(3)增大微分常数系统快速响应性提高,但稳定性降低。
根据PID参数变化对系统动态特性的影响,笔者通过遗传算法求解系统最优参数。
参数优化的目标为降低系统稳态误差,提高系统稳定性及快速响应性。笔者通过AMESim进行仿真分析,调整kd、ki为(0,1),kp为(0,50),设定活塞杆最大位移为20 mm;约束条件为活塞杆最大移动速度,其于2 s~10 s稳定时波动及静态误差最小,选取基因交叉概率及变异概率分别为0.8、0.05,种群范围为50,迭代次数为40,变异幅度为20%。
笔者通过AMESim遗传算法优化模块,获取PID优化参数为:kd=0.994,ki=0.996,kp=20.022。
笔者对优化参数进行仿真分析。液压缸出口压力P变化曲线如图6所示。
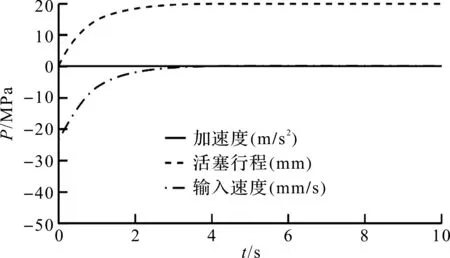
图6 优化后液压缸出口压力
由图6可知,PID参数优化后,系统快速响应性明显提高,虽后期具有小压力波动,但超调量低于3%,系统整体动态特性得到提高。
3 单臂ADAMS建模仿真
3.1 单臂ADAMS建模
笔者通过ADAMS对负载力在单臂位姿改变时的变化进行建模仿真[8]。由于ADAMS直接建模困难,笔者通过SolidWorks建立单臂模型,并将其导入ADAMS[9-10]。
此处设定各组成部件材质为钢,密度为7 800 kg/m3,泊松比为0.29,弹性模量为2.07×105N/mm3。
组件之间的约束关系如表1所示。

表1 组件连接类型
笔者按表1添加约束条件,获得ADAMS模型。
3.2 单臂工作空间分析
单臂末端可达范围为单臂工作空间,笔者通过蒙特卡罗法确定单臂工作空间[11]。
(1)通过ADAMS中RAND函数,生成若干0~1随机数。
则活塞杆伸出量为:
si=smin+(smin-smax)·rand(j)
(2)
式中:si—第i各活塞杆伸出量,mm,i=1,2,3,4;smin—活塞杆最小伸出量,此处取0;smax—活塞杆最大伸出量,此处取100 mm;rand(j)—内置随机函数,产生个0~1随机数,j=10 000。
(2)通过批量处理,获得末端点坐标值。
笔者根据各坐标值,通过MATLAB绘制三维图形。
伞臂工作空间投影如图7所示[12]。
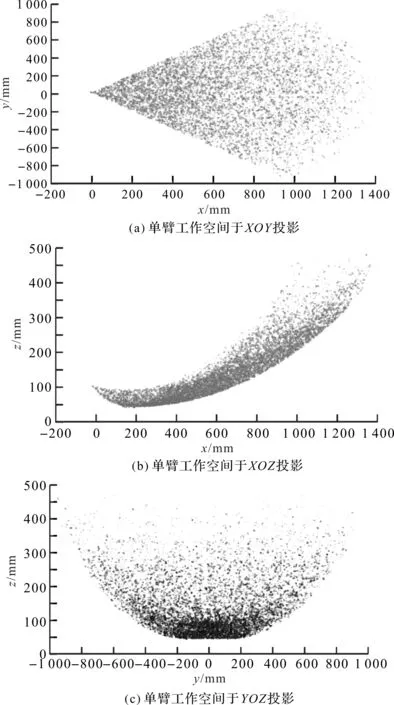
图7 伞臂工作空间投影
由图7可知,伞臂以旋转臂为中心工作空间近似对称,且临界空间于高度方向为近似光滑曲面。
4 变负载下活塞杆位移分析
由于液压缸负载随单臂位姿变化而变化,笔者需要对于优化后的液压系统进行分析;在ADAMS仿真分析中,钻臂液压缸及大臂液压缸输入斜率分别为5和9,获得单臂位姿。
笔者分别将钻臂及大臂液压缸受力情况加载于液压系统AMESim模型中,对比例换向阀施加斜坡控制信号,设定时长为5 s。
由于钻臂及大臂结构均匀,位姿调整时负载力变化近似线性,即:
f1=208.19t-8.1375
(3)
f2=30.821t+118.23
(4)
式中:f1,f2—大臂、钻臂液压缸负载力,N;t—单臂动作时长,s。
笔者设定仿真中活塞杆位移为实际位移,将其与虚拟样机位移进行比较,获得变负载下位姿调整时位移l情况,其对比如图8所示。

图8 活塞杆位移对比
由图8可知:动作开始时机械臂自重由连接铰链平衡,负载力较小,液压缸理论位移小于实际位移;位姿改变,负载力增大,理论位移逐步增加并大于实际位移。
大臂、钻臂液压缸相对位移误差ε1、ε2为:
ε1=1.561/24≈0.065
(5)
ε2=2.6/43≈0.061
(6)
笔者将固定架底座中点设定为起点,机械臂末端位移幅值l及误差ε对比如图9所示。
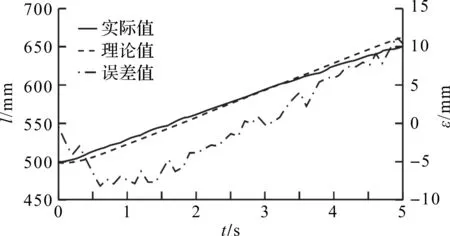
图9 机械臂末端位移幅值及误差对比
由图9可知,该过程中误差最大值约为11 mm。
综合分析井下实际工况可知,笔者所提出的优化方案可以满足伞钻的精度要求。
5 结束语
由于传统液压伞钻钻孔定位中,定位精度低、自动化程度低,笔者以YSJZ4.8全液压四臂伞钻为研究对象,采用PID算法对液压伞钻液压系统进行了优化设计,得到结果如下:
(1)笔者对伞钻钻臂及大臂液压缸实施闭环控制,并采用改进PID算法对误差信号进行了校正,实现了机械臂的自动化控制;
(2)采用遗传算法对控制系统PID参数进行整定,通过系统的节约信号仿真可知,系统稳定性及快速响应性均明显提高;
(3)通过ADMAS建立伞钻单臂模型,将液压缸负载力加载于AMESim进行仿真,获得了变载荷下液压缸理论位移,并将其与实际位移进行了比较分析,由分析结果可知,优化后系统满足变负载自动化控制要求。
