动态径向基函数代理模型及在减速器优化设计中的应用研究*

2020-12-24戴嘉伟罗伟林

机电工程 2020年12期

戴嘉伟，罗伟林

(福州大学机械工程及自动化学院，福建福州 350108)

0 引言

多学科设计优化(MDO)在众多工程领域已得到广泛运用。复杂非线性系统的优化设计通常具有子学科多、学科之间耦合关系强等特点，进行数值仿真计算需要较高成本，且模拟时间长。为解决多学科设计优化中数值模拟时间长、效率低的问题，研究人员迫切希望有一种计算效率高，且精度又有保证的设计方法。

在该背景下，基于代理模型的优化技术得到越来越多的关注[1]。代理模型的基本思想为通过从样本中采集大量的有特征的样本点，构造出一个计算量小、可替代高精度数值模型的模型。目前，常用的代理模型类型包括：多项式响应面模型(PRS)、Kriging模型、径向基函数(RBF)模型、人工神经网络(ANN)模型等。

与其他几类模型相比，径向基函数模型具有更优越的非线性映射能力。径向基函数代理模型在工程设计优化领域有着广泛的应用，如复杂机械系统的可靠性评价[2]、翼型气动隐身优化[3]、火炮多柔体动力学结构优化[4]、图像的噪声抑制与细节保存[5]等。JIN R等[6]通过优化效率、优化精度等方面的比较，指出径向基代理模型是较可靠的一种代理模型。韩鼎和郑建荣[7]通过对多种代理模型的研究，从拟合精度、鲁棒性、实现难度等多个方面比较，认为径向基函数代理模型有较为突出的拟合能力，并具有很高的鲁棒性。BABAEI M和PAN I[8]通过对多种代理模型进行评估发现，三次径向基函数代理模型是其中最可信赖的。CHENG K等人[9]在基于方差的全局敏感性研究中，对多种代理模型进行了测试，指出径向基函数几乎为所有光滑测试算例提供了理想逼近，且只需要调整一个参数，就能有效处理大量的训练样本。

按照优化过程中代理模型的样本特点和使用方法，代理模型技术可分为静态代理模型与动态代理模型[10]：(1)静态代理模型的样本点数在优化算法迭代开始之前就已经采集好，在优化过程中保持不变。若想要保证代理模型的精度，就需要在初始时采集足够多的样本点，但这样降低了优化效率；(2)动态代理模型在优化过程中会根据给定的规则不断地更新样本点，并重新构造代理模型，整个优化过程中代理模型和样本点都是变化的。与静态代理模型相比，动态代理模型在优化效率与优化精度上都有着明显的优势。

但信赖域方法容易陷入局部最优解。为此，基于最小化置信下限准则的动态代理模型方法[14]被提出，但该方法受限于平衡常数的不确定性[15]。将置信下限与信赖域相结合为提高动态代理模型的优化效率和全局最优解提供了一种有效途径[16]。

笔者提出一种基于径向基函数，联合自适应置信下限与信赖域的动态代理模型优化策略(self-adaptive lower confidence bound and trust region-dynamic radial basis function， ALCBTR-DRBF)。在优化迭代的过程中，以代理模型预测值与真实模型响应值之间的误差作为确定置信下限公式中的动态平衡常数的依据，应用遗传算法对置信下限进行优化，然后根据代理模型与真实模型的拟合程度更新信赖域信息，在新的信赖域内选取并新增样本点更新径向基代理模型，最后将该优化策略用于数学测试算例与NASA减速器优化设计中，以证明该优化策略的有效性。

1 动态代理模型构建

1.1 径向基函数

径向基函数具有结构简单、计算效率高的优点，可适用于复杂的高维非线性问题[17]。应用该函数，基本计算思路为：在d维空间中抽取n个初始样本点x1,x2,…,xn∈Rd，目标或约束的真实响应值为y(x1),y(x2),…,y(xn)，径向基函数基本形式为：

(1)

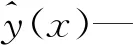
若满足：

(2)

则式(1)可写为：

Y=Φ·W

(3)

(4)

式中：W—权系数向量，W=(w1,w2,…,wn)T；Y—样本点的真实响应值，Y=(y1,y2,…,yn)T；Φ—径向基函数。

常用的径向基函数包括高斯函数、三次函数、逆多二次函数以及多二次函数等。笔者使用逆多二次函数，其数学表达式为：

(5)

式中：r—预测点与样本点之间的欧氏距离；c—形状参数，c为正常实数，通常取值范围为(0，10)。

1.2 置信下限准则

1.2.1 样本更新

在动态代理模型的优化过程中，常用的样本点更新方法有：期望改进(expected improvement，EI)准则和最小化置信下限准则。此外，SBESTER A等人[18]提出了一种并行加点的方法，并结合径向基函数验证了其有效性。

进行样本点更新时，传统的EI准则每次迭代更新都会计算任意点相对代理模型当前预测最优值的改善期望，添加可被改善期望值最大的点，能较好地平衡搜寻的全局性与效率。当预测标准差较小时，搜寻将在当前预测值附近，强化局部搜索能力；当预测标准值较大时，搜寻重点将转移到预测精度低的区域，从而提高全局搜寻能力。传统的EI准则要根据期望函数计算空间中每个样本点的期望值，在复杂问题中计算量偏大、效率降低。因此，置信下限准则被提了出来。

置信下限准则一般表示为[19]:

(6)

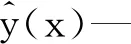
假设径向基函数每个确定性响应值y(x)是某个随机过程Y(x)的实现，利用n个响应的分布Y=(y(1),y(2),…,y(n))，可求出假设的随机过程在xn+1处的方差为：

(7)

当平衡常数w=0时，置信下限准则与预测值等价，此时搜索重心将放在当前预测值周边，提高局部搜索能力；当w→+∞时，预测值对整体表达几乎不产生影响，置信下限准则将等价于最大化预测标准差，搜索重心从预测值周边转移到预测精度较低的部分，搜索范围从局部过渡到全局并加强全局搜索能力，且使问题变为最小化问题。

为减少置信下限准则中平衡常数w因人为经验确定所带来的误差与波动，常采用一种自适应平衡常数置信下限方法。

1.2.2 平衡常数的自动确定

通过代理模型预测值与真实模型响应值之间的误差与预测标准差的比较，可确定平衡常数为:

(8)

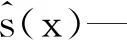
1.3 信赖域方法

信赖域方法常被用来解决非线性规划问题，其核心思想是在每次迭代时，在一个选定的可信赖区域内，利用近似模型在当前中心点拟合真实模型，通过优化算法寻优得到当前近似模型最优解，将其作为下一次优化迭代时信赖域区域更新的起始点。该方法通过近似模型与真实模型的拟合程度，判断是否需要缩放信赖域空间。若当前近似模型满足精度要求，则扩大信赖域搜索范围；否则缩小信赖域搜索范围，保证下次优化结果的精度。如此反复迭代更新直至获得真实模型最优解。

对于任意非线性目标函数f(x),假设近似模型mk(p)=f(xk+p)，在第k次迭代中的增量p为：

(9)

式中：Δk—信赖域半径。

假定在优化过程的第k步增量为pk，则目标函数在第k步的实际下降量记为：

Aredk=f(xk)-f(xk+pk)

(10)

近似模型的下降量记为：

Predk=mk(0)-mk(pk)

(11)

参数Δk的选定一般根据下式进行调整：

(12)

式中：rι—近似模型与目标函数的近似程度。

rι越接近于1表示近似程度越高，此时可以适当扩大信赖域半径；反之，则需对Δk适当缩小。信赖域方法通常使用Taylor展开式逼近原函数，涉及到复杂的Hessian矩阵计算，使整体计算量偏大。因此，笔者使用径向基代理模型替代Taylor展开式来逼近原函数。

2 ALCBTR-DRBF优化策略描述

2.1 优化策略

基于所采用的最小化置信下限方法，优化问题可用如下模型表示：

(13)

s.t.hj(x)=0j=1,2,…,J

gk(x)≤0k=1,2,…,K

xL,i≤xi≤xU,ii=1,2,…,nv

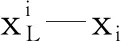
约束条件为真实模型所具有的约束，其优化流程如图1所示。

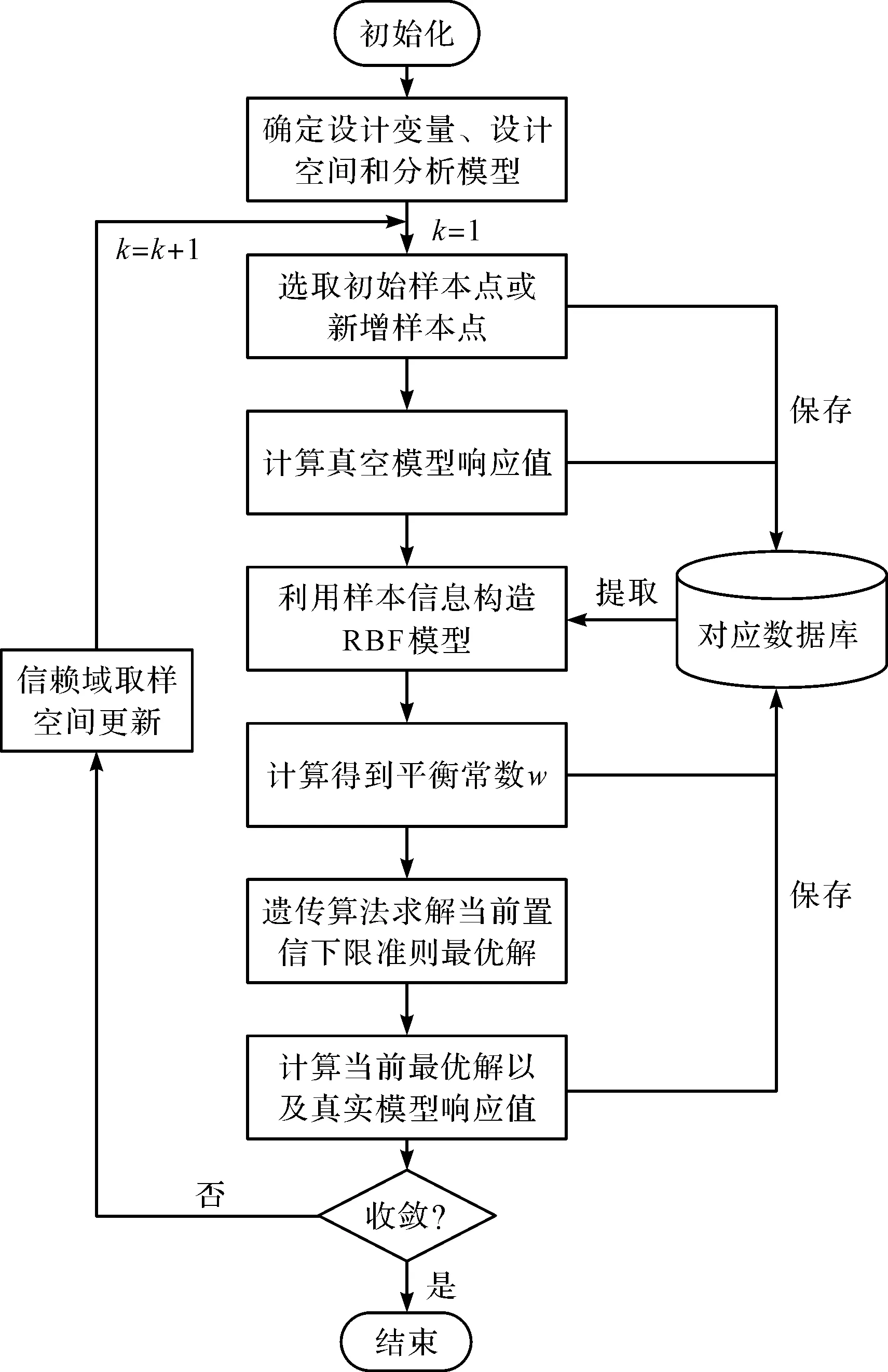
图1 优化流程图

具体步骤如下：

(1)确定设计变量与设计空间D，建立分析模型；令迭代计数参数k=1，通过最优拉丁超立方采样方法[20]选取初始样本点(循环中为新增样本点)。在选取初始样本点时，样本点数量通常为设计变量数的3到6倍，笔者选取初始样本点数为：

(14)

(2)当k=1时，初始信赖域采样空间S1为整个设计空间，即S1=D。当k>1时，信赖域空间是已更新的采样空间；计算真实模型对应初始样本点(循环中为新增样本点对应的响应值)，然后将样本点和响应值储存到相应数据库中；

(3)根据所获得样本构建径向基函数模型。依照已知信息和公式(13)获得平衡常数w，根据式(6)确定置信下限；

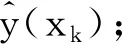
(5)将第k次优化所得到的可能最优解xk代入真实模型，得到对应真实响应值f(xk)，并将xk和f(xk)存入数据库；

(6)判断是否满足收敛标准。当k=1时，直接转入步骤7；当k>1时，计算优化过程中第k次与第k+1次所对应最优解的真实响应值之间的相对误差，判断该误差是否满足收敛判定条件。若满足，循环停止，优化流程结束，步骤(4)中所得最优解即为真实模型最优解。若不满足，则转入步骤(7)；

(7)根据已知信息更新信赖域采样空间。令迭代参数k=k+1，转至步骤(2)。

2.2 信赖域更新策略

信赖域更新方法使用目标函数值的下降程度作为更新准则，能够对采样空间进行合理缩放，提高局部优化的精度与效率。笔者以最小化问题为例，信赖域更新的目的是使优化迭代时，基于当前代理模型的优化，实现目标函数的真实值的显著下降。具体的更新步骤如下：

(1)确定信赖域采样空间新的中心点xc。若目标函数的真实值下降，即y(xk-1)-y(xk)>0，则将当前可能最优解xk作为更新的中心点，否则使用上一次的可能最优解xk-1作为信赖域采样空间更新的中心点；

(2)根据参数rι来调整信赖域半径Δk，依据如下：

(15)

式中：c1，c2，r1，r2—常数；δ—最大信赖域半径。

δ可取为初始设计空间半径R。利用信赖域准则更新样本空间，为避免数次迭代后出现信赖域半径过小或信赖域半径过大的问题，此时可使用文献[21]的方法进行处理，得到更新之后的信赖域区域：

(16)

式中：xlbc—信赖域采样空间的下边界；xubc—信赖域采样空间的上边界；λR—最小信赖域半径。

为了使优化策略更好地跳出局部最优解，给定最小信赖域半径λR。其中，λ为常数，可根据不同的优化问题取不同的值。

3 测试算例

3.1 数值测试算例

首先，选用SC函数和GN函数作为测试函数。

(1)SC函数表达式为：

(17)

该函数是两变量、单峰函数，又称六背驼峰函数，有2个全局最优解和4个局部最优解，全局理论极小值为-1.031 6。

(2)GN函数表达式为：

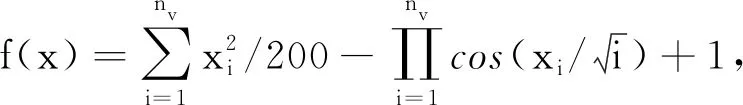
(18)

可见该函数是两变量函数，全局理论极小值为0。

笔者使用所提出的ALCBTR-DRBF优化策略，与动态径向基函数代理模型(DRBF)策略、基于信赖域的动态径向基函数代理模型(TR-DRBF)策略、基于传统置信下限(w=1)的动态径向基函数代理模型(LCB-DRBF)策略、基于最小化置信下限与信赖域的Kriging动态代理模型策略(IMLCB-TR)，分别对SC函数和GN函数进行优化，对优化性能进行比较。

信赖域方法参数取值如下：c1=0.75，c2=1.25，r1=0.1，r2=0.75，λ=0.05。取10次优化结果的中位数作为最优解，模型调用次数取10次优化调用次数的平均值。

优化结果对比如表1所示。

表1 优化结果对比

模型调用次数对比如表2所示。

表2 模型调用次数对比

由表1和表2可知：(1)针对SC函数，笔者所提出的ALCBTR-DRBF策略拥有最高的精度，且有着最少的模型调用次数；(2)针对GN函数，ALCBTR-DRBF策略所得的最优解中间值与全局最优解非常接近，在精度和效率方面都明显优于其他4种方法；(3)在优化效率方面，DRBF调用模型次数最少，仅为133次，但该方法明显陷入了局部最优的情况。

综上所述，ALCBTR-DRBF优化策略在全局性和收敛性上有着更好的表现。

3.2 NASA减速器优化设计实例

为了验证该优化策略在工程优化领域的有效性，笔者选用了MDO领域经典算例—NASA齿轮减速器[22]。该优化问题可概括为：在满足齿轮弯曲应力、接触应力和扭转变形的前提下，使减速器的体积(质量)最小。

减速器结构如图2所示。

图2 齿轮减速器结构

该算例的数学模型如下[23]：

(19)

式中：x1—齿面宽度，2.6≤x1≤3.6；x2—齿轮模数，0.3≤x2≤1.0；x3—小齿轮齿数，17≤x3≤28；x4，x5—两齿轮轴承间距，7.3≤x4≤8.3，7.3≤x5≤8.3；x6，x7—两齿轮轴轴径，2.9≤x6≤3.9，5≤x7≤5.5。

该优化设计问题的约束为非线性，笔者假设目标函数是一个高精度分析模型，真实模型约束为约束条件；分别比较ALCBTR-DRBF策略与DRBF策略、TR-DRBF策略和MLCB-DRBF策略的优化结果，如表3所示。

表3 优化结果

由表3知：(1)该算例理论最优解为2 994，ALCBTR-DRBF策略所得优化结果与理论最优解误差仅为0.006%，而DRBF策略、TR-DRBF策略、LCB-DRBF策略、IMLCB-TR策略与最优解的误差分别为6.5%、1.4%、9.0%、0.05%；(2)笔者提出的优化策略调用分析模型的次数分别是DRBF策略、TR-DRBF策略、LCB-DRBF策略、IMLCB-TR策略分析模型调用次数的26.3%、62.4%、39.7%和43.0%。

由此可见，从优化精度与优化效率来看，笔者所提ALCBTR-DRBF策略均优于DRBF策略、TR-DRBF策略、LCB-DRBF策略和IMLCB-TR策略。