广西老年高血压患者住院费用的影响因素

高洪达 冯启明 陈荷 徐婷婷 骆国盛 赵劲民

(1广西医科大学信息与管理学院，广西 南宁 530021；2广西中医药大学公共卫生与管理学院)

据统计，我国的高血压患者已超过2亿人，而60以上老年人高血压患者占40%～50%〔1〕，平均每两个老人中就一个患有高血压，高血压已经成为危害我国老年人健康的重大的个公共卫生问题〔2〕。但是，由于高血压多病情复杂、病程较长且不容易治愈，需要消耗较多的医疗卫生资源，不仅给高血压患者带来较大的经济负担，还不断助推着住院费用的增长〔3〕。从2004年开始，我国心脑血管的住院费用不断上升，增速甚至超过了国民生产总值(GDP)〔4〕。本文旨在分析高血压患者住院费用的影响因素。

1 资料来源与方法

1.1资料来源 数据来源于广西某大型三甲综合医院2012～2016年病案首页，根据国际疾病分类标准(ICD-10)，选取出院诊断为高血压1级165例、高血压2级796例和高血压3级2 060例患者，ICD-10分类为I10.X03、I10.X04、I10.X05。通过HIS系统收集住院患者病案首页信息，剔除标准：数据缺失、住院天数低于2 d或者高于90 d及住院费用500元以下或10万元以上的病例予以剔除，经筛选共有3 021例住院患者进入研究。指标的选择根据病案首页所能收集到的信息，其中费用指标采用高血压患者住院总费用；影响因素指标：性别、民族、婚姻、血型、入院途径、医疗付款方式、高血压等级、年龄、住院次数、并发症数量及实际住院天数等。软件的选择：数据存储选用Microsoft Visual FoxPro9.0软件，数据的筛选及多元线性回归拟合分析采用 SPSS19.0软件进行，对于BP神经网络(BPANN)的数据拟合分析采用Clementine12.0 进行。

1.2BP ANN模型

1.2.1基本原理 人工ANN是一种模拟生物神经网络的数学模型，它从信息处理的角度对人脑的神经元网络进行抽象，并根据连接方式的不同组成不同的网络模型。BP ANN是人工ANN的一种，是按误差反向相传播训练的多层前馈网络，基本思想是梯度下降法，利用梯度搜索技术实现网络期望输出和实际输出的误差均方差最小，基本结构见图1。

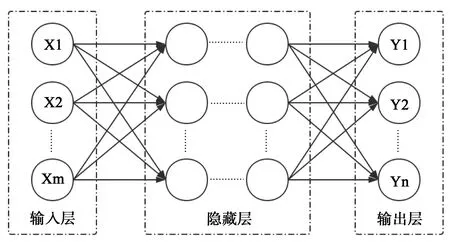
图1 BP ANN模型算法结构图

BP ANN包含输入层、隐藏层和输出层，每一层包含若干神经元，不同层神经元之间由权值w连接，其基本过程包含信息的正向传播和误差的反向传播：信息的正向传播时，信息从输入层经过隐藏层处理后进入输出层，如果输出的信息达不到期望水平，则进入误差的反向传播，即将误差信号沿原来信息在神经元间传播的路径返回，在返回的过程中逐个修改各层中神经元的权值。此过程不断循环，权重不断调整，直到实际输出和期望输出间的误差达到允许的范围内，这也是ANN的训练过程〔5～7〕。

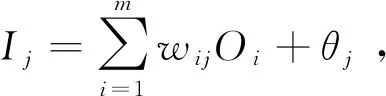
Δwij=l×ErrjOi(权重增值)；wij=wij+Δwij(权重更新)

Δθj=l×Errj(偏差增值)；θj=θj+Δθj(偏差更新)。

其中，l是学习率，通常取0～1之间的常数值。

④若前一周期所有的△wij都小于某个阀值或错误率小于某一阀值或者超过预先制定的周期数，则终止训练；否则输入下一样本，带入①继续训练。(4)网络测试：使用测试集对训练所得的网络模型进行测试。

1.2.3多元线性回归模型 多元线性回归法是研究多个自变量和一个因变量之间的线性关系的方法，是以多个自变量的已知值为条件的回归分析。多元线性回归分析法的数学模型为：Y=β0+β1X1+β2X2+…+βPXP，其中Y为因变量，Xi为自变量(i=1，2，3，…，p)，βi为Xi回归系数，可根据模型中回归系数的大小判断自变量对因变量的影响大小。待模型各变量系数求出后，需对模型整体线性的意义进行检验(方差分析，α=0.05)及对各变量系数及常量的意义进行检验(t检验，α=0.05)。

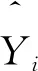
2 结 果

2.1住院费用一般情况 不同高血压等级间住院费用差异无统计学意义(高血压1级7 040.25元、2级7 173.29元、3级7 365.95元，Z=2.769，P=0.25)。

2.2分类变量的赋值 分类变量赋值：X1：性别(男=1，女=2)、X2：民族(汉族=1，壮族=2，其他=3)、X3：婚姻〔未婚=1，已婚=2，丧偶=3，离婚=4(剔除婚姻为“其他”的类别)〕、X4：血型〔A型=1，B型=2，O型=3，AB型=4，未查=5(剔除血型“不详”的类别)〕、X5：入院途径〔急诊=1，门诊=2，其他医疗机构转入=3(剔除入院途径为“其他”的类别)〕、X6：医疗付款方式(剔除组内样本数小于5的分组)〔城镇职工医保=1，城镇居民医保=2，新农合=3，全公费=4，全自费=5，其他付款方式=6(剔除医疗付款方式为“其他”的类别)〕、X7：高血压等级(高血压1级=1，高血压2级=2，高血压3级=3)、定量变量：住院次数(X9)、年龄(X8)、实际住院天数(Xi1)、并发症数量(X10)赋值为原始值。

2.3BP ANN模型分析 经BP ANN分析，模型估计准确度为96.944%，输入层包含31个单元，隐藏层(1层)包含39个单元，输出层为1个单元，训练集和测试集分别占样本量的70%和30%，各影响因素重要程度：实际住院天数为59.8%、并发症数量为10.5%、医疗付款方式为7.5%、住院次数为6.0%、入院途径为4.8%、婚姻为3.2%、血型为3.2%、性别为1.6%、年龄为1.4%、民族为1.1%、高血压等级为1.0%，可知经BP ANN模型的分析，各变量重要程度排名前2分别为实际住院天数和并发症数量，重要程度在10%以上。

2.4多元线性回归模型分析结果 根据单样本的Kolmogorov-Smirnov检验得出，统计量Z=10.803，P=0.000<0.05，住院费用变量不符合正态分布，因此不同组建费用的比较采用分参数检验，具体选择多个样本的Kruskal-WallisH检验。分析得出仅有婚姻、血型、性别和医疗付款方式变量组间存在差异(见表1)，因此将婚姻、血型、性别、医疗付款方式以及定量变量(住院次数、年龄、实际住院天数、并发症数量)作为多元线性回归模型自变量进行下一步分析。

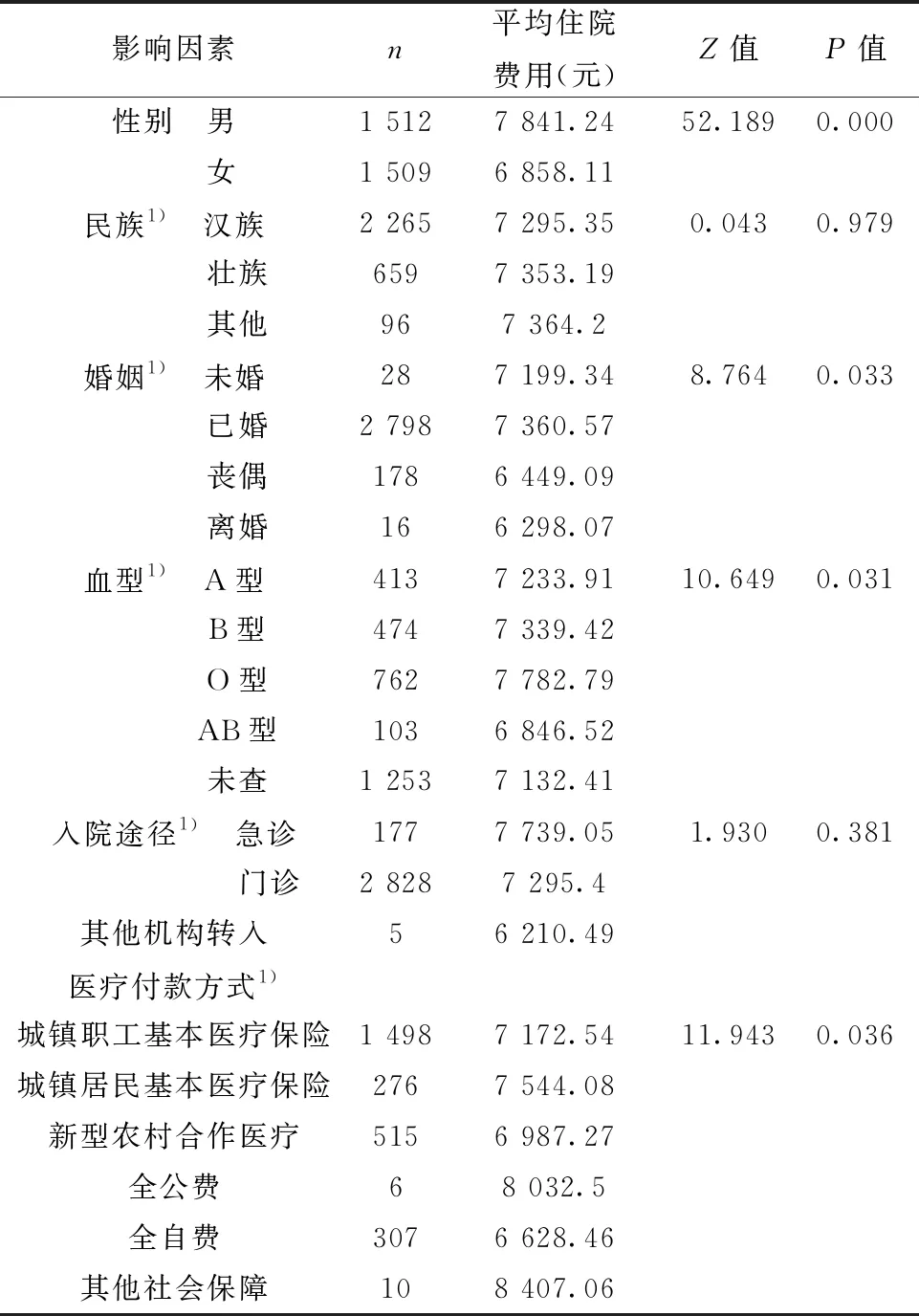
表1 分类变量的非参数检验结果

经Kruskal-WallisH检验经得出，仅X1、X3、X4、X6变量的住院费用差异有统计学意义(P<0.05)，因此将该4个分类变量纳入多元线性回归模型自变量。在带入多元线性回归方程前，需要对分类变量进行哑变量的转换，其中将男性、已婚、血型O型、医疗付款方式城镇职工基本医疗保险的类别设为参考变量。进而以性别、婚姻、血型、医疗付款方式、实际住院天数、并发症数量、住院次数及年龄为为自变量，住院费用为因变量进行多元线性回归分析，经多元线性回归模型拟合后得出，回归方程为：Y=1 300.939+701.718×X11+513.527×X10-1227.028×X4(X4=5)-1 287.864×X1(X1=2)-60.764×X9+677.873×X4(X4=2)+5 141.983×X6(X6=4)，见表2。

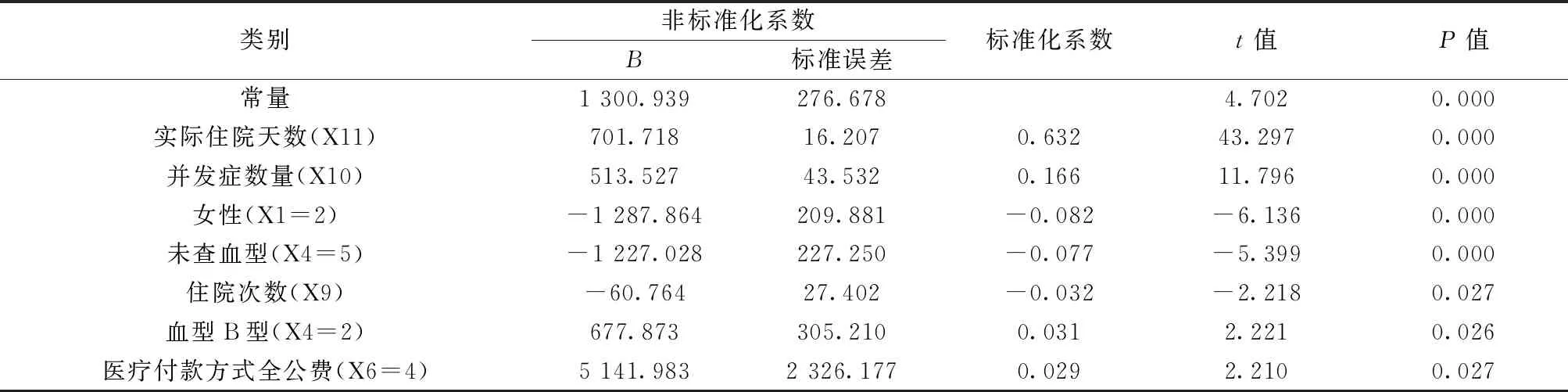
表2 多元线性回归分析结果

方差分析得出方程F=402.884，P=0.000<0.05，回归方程有意义。

从多元线性回归分析的结果中，可以了解到各因素对老年高血压住院费用影响具体的数值关系，其中实际住院天数、并发症数量、血型B型、医疗付款方式全公费与住院费用呈正相关，回归分析中所选取的参考类别为O型血，即B型血高血压患者的住院费用比O型血患者高677.873元，而医疗付款方式变量所选取的参考类别=城镇职工基本医疗保险，即全公费高血压患者的住院费用比城镇职工医保患者高5 141.983元。

负相关的自变量有女性、血型未查和住院次数，表示女性高血压患者的住院费用比男性患者低1 287.864元，未进行血液检查的高血压患者的住院费用比查血为O型血患者低1 227.028元，高血压患者住院次数每增加一次住院费用减少60.764元。见表2。

2.5两模型误差结果 通过对两种方法模型的误差指标的计算，得出BP ANN模型的调整R2高于多元线性回归模型，RMSE的比较显示，BP ANN模型误差相对要小，见表3。

表3 两种模型误差对比

3 讨 论

本研究结果暗示未知因素对老年高血压住院费用存在影响。综合两个模型拟合结果，实际住院天数和并发症数量因素为老年高血压患者住院费用的主要影响因素。

实际住院天数对住院费用产生正向影响在很多学者的研究中有出现〔10～13〕，属于医院可以控制的因素，住院天数的增加必然消耗更多的医疗资源，需要更多的治疗、药品、检查等。因此，在保证医疗质量的前提下，适当降低住院患者平均住院日，不仅可以降低患者医疗费用，还可以提升病床的使用效率，减少医院资源的浪费和不必要医疗行为的发生。有研究显示〔14〕，临床路径不会因为病人或者医生的不同，导致住院天数或者费用的差异，从而达到规范医疗行为，提高服务效率，减少住院天数和医疗资源的浪费，从而达到降费的目的。并发症的数量虽然不属于医院的可控范围，但与住院天数类似，并发症越多同样需要更多的治疗或检查，进而导致费用的增加。

B型血高血压患者住院费用比O型血高，根据李宗智等〔15〕研究，可能是由于B型血患者学业黏稠度高，容易形成脑血栓，进而增加高血压患者的住院治疗难度；而对于未进行血液检查的高血压患者住院费用低，原因可能在于未进行血液检查意味着省去了部分检查费用，或者是病情较轻不需要进行血液检查，治疗难度低，而费用也自然相对较低。性别方面对高血压患者住院费用的影响，与其他研究结果类似〔16〕，可能是由于男女患者生理结构或体制上的差值，导致治疗方案和医疗资源需求量的不同，引起的费用差异。

住院次数，即本次住院为第几次住院，从多元线性回归分析的结果可以看到，该因素与住院费用呈负相关关系，即住院次数越多，所产生的住院费用越低，原因可能在于住院次数越多，对自身疾病越了解，且有前期的病例记录，省去了一些重复的检查等环节，医院对患者的治疗更有针对性，进而对手术或者用药会更明确，实现降费的效果。

对于医疗付款方式对住院费用的影响主要体现在，全公费高血压患者的住院费用较高，此类结果在其他学者研究中也有所出现〔17〕，原因可能在于对于医保患者而言，虽然医疗保险可以报销一部分，但是自身也要承担一部分费用，因此会对治疗或药物的价格有所顾忌，会尽量减少不要的检查，而全公费的患者由于住院费用全部报销，因此在治疗过程中不会过多在意治疗药物和检查项目的价格情况，进而导致需求膨胀，追求更好的医疗服务〔18，19〕；对于医院而言，由于医保对医院总量控制，所以医院也会尽量减少药品或检查的开支，也会导致医保患者比公费患者费用低。

ANN模型处理非线性数据资料能力比传统方法要强〔20〕。而且神经网路模型对数据资料的分布情况无要求，具有容错性，因此可以运用神经网络模型处理复杂问题，例如费用的预测等。而多元线性回归模型在进行数据的拟合过程中，容易受到变量间相关性的干扰，且在有等级或者分类数据资料时，结果容易受到等级或者类别物理数值的影响，进而出现偏差〔7〕。两种方法结合使用可增加结果的科学性和可信度，针对两种模型的特点和优势，可以采用神经网络进行费用的预测，使用多元线性回归模型直观反映各因素与费用间的具体数值关系。

本研究两模型的误差分析结构说明ANN模型对数据的拟合效果更好，此现象和其他学者〔20〕研究相类似。而多元线性回归模型给出的结果仅能解释患者住院总费用信息量的48.35%(R2=48.35%)，剩下的51.65%的信息通过其他未研究到的因素来解释，如某些由于未考虑到或技术手段无法获知等原因，未纳入该研究的因素所造成的影响，例如政策的刺激、技术设备的提升、费用结构调整或医保制度的改变等因素，这一点也提示仍然有很多影响因素需要进一步探讨。