Culture Merging:A Logic Based Method*
2020-12-24XiaoxinJing
Xiaoxin Jing
Abstract. Intercultural conflict resolution is an important issue worldwide.However,we should avoid resolving them by war,violence,or even terrorism.To this end,this paper proposes a logic based merging method to resolve opinion conflicts on the same things in different cultures.Specifically,we first define each agent’s logic system,in a specific culture,as a tuple of the language and a binary relation over the language,which can well reflect different opinions on the same things in different cultures.Then we define a kind of the Hamming distance to measure the distance between any two cultural logic systems.Further,based on the distance measure,we define a kind of merging operator (including its special cases such as impartial merging operator,cautious operator,and tolerant merging operator)and reveal some of their properties such as consistency,agreement,strong unanimity,groundedness,anonymity,majority preservation,and uniqueness.In addition,we propose a method for merging cultural logic systems with different degrees of importance and with opinions which are important differently.
1 Introduction
Culture is a collection of elements,such as values,beliefs,opinions,and knowledge of the world,shared by a group of human beings.([13])Generally speaking,conflict means some form of friction,disagreement,or discord arising within a group.([2])Therefore,cultural differences can cause cultural conflict.([29])The study of conflict resolution started centuries ago,but only recently this problem was systematically investigated because conflicts between different cultural groups are among the most difficult problems we are facing today.For these conflicts,of course,we should avoid resolving them by war,violence,and terrorism.As a result,it is very important to investigate other more acceptable ways for achieving consensus,so that social problems caused by the conflicts of different cultures can be resolved peacefully.([25])Moreover,a study on intercultural resolution can also benefit governments to make their policy concerning immigration,because such a method can be used to predict what kind of a new culture will appear if they grant immigrants with different cultural background.In addition,if agent systems act on behalf of humans in different cultures,they have to model accurately their human users’interests,preferences,and prejudices; otherwise,their human users would not delegate their tasks to the agents.([12])
So far,to resolve intercultural conflict,much work has been done.Nevertheless,most of them are sociological or anthropological theories.([3,6,1])The formal theories of intercultural conflict resolution focus on intercultural negotiation([30,15]),which all are game-theoretic approaches instead of logical-based ones.Nonetheless,the game-theoretic approaches can just be used to figure out which strategy is the best one in a particular intercultural negotiation scenario,and they cannot be used to predict what kind of new culture will appear if people with different cultural opinions on the same things are put together.
On the other hand,merging is a process for agents to fuse conflicting information from several sources with equal reliability to build a coherent description of the world.([36])A lot of formal theories about merging have been developed ([34,35,28,19]),and most of them focus on the problem of belief merging in the same culture.However,from the viewpoint of cultural pluralism and the information processing in intercultural communications,these merging theories need to be extended to intercultural environments.For example,when two friends,Chinese Xiaoming and American Angela,meet in the street,Xiaoming asks Angela,“Where are you going?”For Xiaoming,this is just a kind of daily greeting in China;but Angela may feel uncomfortable and view it as an invasion upon her privacy.Therefore,in an intercultural communication,not only the language barrier but also the logic systems reflecting their cultural characteristics(unnecessarily the same)prevent people from different cultures to understand each other.In other words,different cultures may be modelled as different logic systems.As far as we know,at present researchers in merging theories presume a unified underlying logic system,while individuals or groups from different cultures often reach different,even opposite,conclusions even from the same precondition.([38,27])
To this end,this paper will propose a merging method in the context of intercultural communication.More specifically,we will design a distance-based operator to merge logic systems that model different cultures.This brings a number of new challenges.That is,we need not only to merge logical languages but also to reach coherent binary relations over the languages.Actually,such a binary relation represents an implication relation in a logic system,which reflects the opinion on a thing in a specific culture,e.g.,the question of“where are you going?” is a“daily greeting”or an“invasion upon privacy”.
We advance the state of art in the following aspects.(i)We model different cultural opinions on the same thing as a binary tuple,where one element is some propositions about the thing and the other is a proposition that reflects the opinion on the thing in a culture.In other words,we define each agent’s logic system as a pair,which consists of the language and a binary relation among the language.(ii)We propose a two-step process to merge different cultural logic systems:first all the logic systems are expanded to be based on the same language,and then the distancebased method is employed to select the logic system that is nearest to the expanded logic systems.(iii)We introduce three special merging operators:impartial merging operator,cautious operator,and tolerant merging operator.(iv)We reveal some basic properties of our merging operator.And(v)we also propose a solution to the problem of merging cultural logic systems with different degrees of importance and opinions which are important differently.
The rest of this paper is organised as follows.Section 2 defines the logic systems of different cultures.Section 3 discusses how to merge the logic systems by using the distance-based approach.Section 4 reveals some properties of our merging operators.Section 5 we discuss how to merge cultural logic systems with different degrees of importance and with opinions which are important differently.Section 6 discusses the related work to show how our work advances the state-of-art in the research area of information fusion.Finally,Section 7 concludes this paper with future work.
2 Cultural Logic Systems and Their Expansions
This section will define the cultural logic systems of agents from different cultures.
There are several different perspectives to consider the notion of logic.Firstly,the classical logic systems,which were introduced by Frege and Rusell ([14]),are defined as a set of valid formulas in some logic system.Specifically,a logic system is given by a formal language and a deductive calculus(namely a set of axioms and a set of inference rules).The total formulas derivable in the calculus,which are valid in the system,compose the logic system.This view has been proved to be too narrow because of the emergence of numerous non-classical logics,in particular,logics without valid formulas at all,such as Kleene’s three-valued logic([10]).In this paper,we adopt another abstract approach and define logic as a pair(S,⊢),where S is the set of sentences and ⊢⊆P(S)×S is the consequence relation.Such pairs are used,for example,as entailment systems in[26],or logical systems in[39].
Now let L be a fixed language(i.e.,a set of sentences).Here,we do not give a specific definition for language L,just assume that it is formal.It may have a set of connectives(with an arity n),a set of propositional variable V,and formulas in L are defined inductively as usual in propositional logic.In intercultural communication([16]),agents from different cultures may have different languages,which we represent as L,and restrict them to finite set of sentences.Thus,a cultural logic system includes a kind of language L and a set of binary relations R⊢between P(L)and L,1The binary relation indicates that given some sentences in P(L)as premises,we could get a sentence in L as their conclusion.Besides,we think that in the different cultural logic systems,the monotonicity is not necessarily satisfied.where P(L)is denoted as the power set of L.Formally,we have:
Definition 1(Cultural logic system).Given a formal language L,which is a finite set of sentences,a cultural logic system over L is a pair L=P(L)×L.We denote a profile of n cultural logic systems as P=(L1,...,Ln),where eachis the cultural logic system for agent i.
In the rest of our paper,sometimes we will useto denote the complete version of a cultural logic system,wherebut we will not distinguish these two notations if there are no confusions arisen.
Intuitively,a cultural opinion belongs to a consequence relation in a cultural logic system.Formally,we have:
Definition 2(Opinion).Given a formal logic language L,an opinion in L is a tuple(Σ,φ) ∈P(L)×L,where Σ is a set of premises and φ is a conclusion.An opinion(Σ,φ)is said to be valid in a cultural logic system Liff(Σ,φ)∈.We denote O(L)as all the valid opinions in L.If an opinion(Σ,φ)is not valid in L,then(Σ,φ)
Notice in this paper,we assume a cultural logic system is consistent,i.e.,for anysuch that(Σ,φ) ∈In other words,the above two conflictive opinions cannot be in the same cultural logic system.
Given a profile of multiple cultural logic systems,our purpose is to characterise the set of logic systems acceptable to a group of agents from different cultures.That is,we will give a coherent logic,which is resulted from fusing different cultural logic systems with equal reliability.Thus,our approach is a two-step process.First,each cultural logic system is expanded to a new one over the language considered by the group of agents from different cultures.This aims to reflect that some agents may not know the language given by other agents from other cultures,as well as how to add the sentences and the inference relations based on the sentences into their own logic systems.Then,merging is applied into the expanded systems for resolving the possible conflicts between them.
In order to achieve this goal,we first introduce the concept of cultural logic systems’expansion.Intuitively,it extends a number of cultural logic systems so as to represent the ignorance of the sentences and implication relations in different cultural logic systems given by agents from different cultures.This is necessary in our setting because the in intercultural communication,agents probably have different languages.Hence,the cultural logic system of each agent is first expanded,and all such cultural logic systems are built upon the same language,in which the sentences are given by at least one agent in intercultural communication.Formally,we have:
Definition 3(Expansion of a cultural logic system profile).Given a cultural logic system profile P=(L1,...,Ln)of n cultural logic systems in which each Li=and a cultural logic systeman expansion of L over P is defined as a cultural logic system exp(L,P)=where:
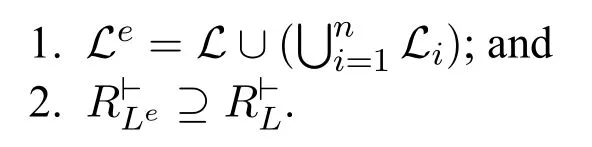
In the above definition, Le=means that Leis the expansion of L over languages Liin the cultural logic system profile P=(L1,...,Ln).As we mentioned before,the languages in different cultural logic systems have different sentences.The expansion of L over Li(i ∈{1,...,n})is obtained just by adding all the sentences occurring in Liinto L.As for the expansion of the implication relation,means that the valid opinions in L are still valid in its expansions.
Besides adding the sentences,we should also consider the implication relations based on the sentence.This is because each agent can have her own expansion policy to incorporate a new implication relation into her cultural logic system.More specifically,we focus on a special one,called the consensual expansion:when incorporating a new implication relation into his/her own cultural logic system,an agent thinks that the premise infers the conclusion whenever all the other agents who are aware of all the sentences do not object to this implication relation;otherwise,he/she thinks that he/she ignores this implication relation.Formally,we have:

The above definition reflects the intuition that given a profile P of multiple cultural logic systems,if valid opinions in one cultural logic system are not conflictive with those in other cultural systems,they should be added into the consensual expansion for all cultural logic systems in the profile.Clearly,the consensual expansion of L over P is also a cultural logic system.
In the following,we will reveal a property for consensual expansion.Before presenting it,we first need two concepts below:
Definition 5(Non-clash part).Let P=(L1,...,Ln)be a profile of cultural logic systems,where each Li=is a logic system.Then the non-clash part of P,denoted as nc(P),is given by:
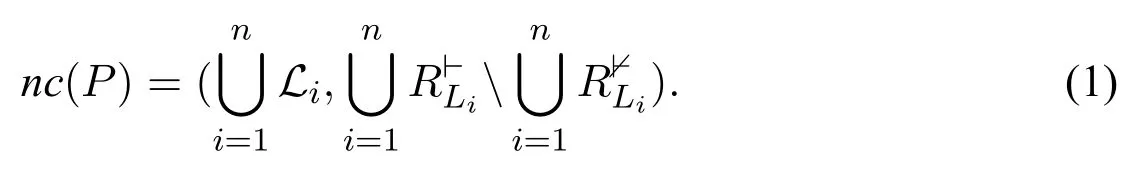
Definition 6(Common part).Let P=(L1,...,Ln)be a profile of logic systems,where each Li=is a logic system.Then the common part of P,denoted as cp(P),is given by:
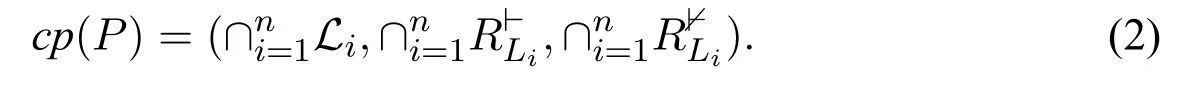
The following theorem reveals an important property of the consensual expansion:when we take the consensual expansion over a profile,the valid opinions in the non-clash part of the profile is always preserved.In other words,any consensual expansion for a logic system over a profile of Lipreserves the pieces of information that are not questioned by any other agent.Moreover,the consensual expansion is the most cautious expansion that one can define because an opinion is added into the merged logic system only when all the other agents do not oppose to it.
Theorem 1.2Some proofs in this paper are omitted due to space consideration,see[17]for details.Let P=(L1,...,Ln)be a profile of cultural logic systems,andbe the consensual expansion of Liover P.Then ∀i ∈{1,...,n},
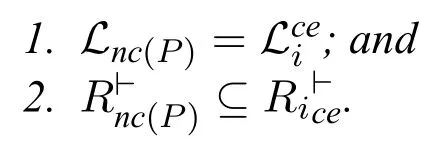
3 Cultural Logic Systems Merging
In this section,we will propose a merging approach on the expanded systems as a way to resolve possible conflicts between them.
3.1 Hamming distance between cultural logic systems
Our method of merging a profile of cultural logic systems is a two-step process.Firstly,each cultural logic system Liover the language of Liis expanded such that all the expansions of the logic systems are over the same language L′=Here we assume that the expansion of each agent’s logic system over the profile is the consensual one.Next,the logic systems over L′are selected with the distancebased method as the result of merging.To do this,we will apply the idea behind the well-known Hamming distance ([36,34])to define the Hamming distance between two cultural logic systems as follows:
Definition 7(Hamming distance between cultural logic systems).Given two cultural logic systems L1and L2over the same language L,their Hamming distance is the number of opinions on which the two logic systems differ,i.e.,
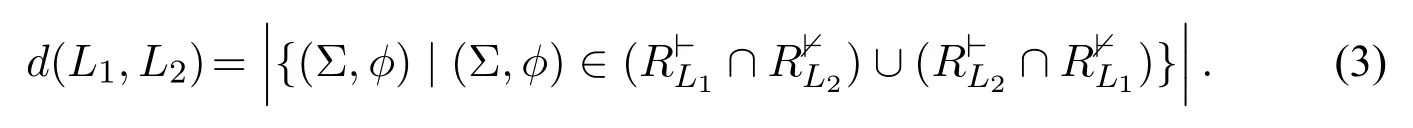
After defining the distance between two cultural logic systems,we need to justify what we did is proper.That is,we need to prove that our definition of the distance satisfies the basic axioms of a distance measure.Formally,we have:
Theorem 2.3See the proof in details in[17].Given any cultural logic systems Li,Lj,and Lkover language L where i,j,k ∈{1,...,n},their Hamming distance satisfies:
1.non-negativity:d(Li,Lj)≥0;
2.identity of indiscernible:d(Li,Lj)=0iffLi=Lj;
3.symmetry:d(Li,Lj)=d(Lj,Li);and
4.triangular inequality:d(Li,Lk)≤d(Li,Lj)+d(Lj,Lk).
3.2 Merging method
Our merging method aims to select cultural logic systems that are as close as possible to the extended systems generated from the original ones of agents in different cultures.We will measure the closeness by the distance between a cultural logic system and a profile of cultural logic systems.Formally,we have:
Definition 8(Cultural logic systems merging).Given a profile P=(L1, ..., Ln)where each Li=is a cultural logic system,let d be a kind of distance between two cultural logic systems.And suppose thatis the expansion of Liover P.Then the merging of P is defined as:
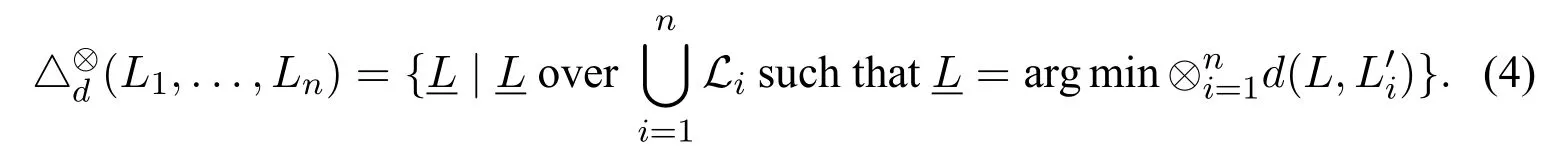
where an aggregation function ⊗is a total function mapping from a finite tuple of non-negative integers to a non-negative integer and satisfies:

In the literature,aggregation function ⊗in the above definition can be in many forms([34,40,24,44,20]),but in this work we just use the normal addition operator,on real number set,as the aggregation function,because it is the most intuitive one.
Generally speaking,given two cultural logic systems L1and L2over the same language of L,since language L is finite,we can suppose the number of the sentences in L is m.Thus,in totalopinions can be generated by language L.4representsindicating the number of ways to select n distinct objects from a set of m objects without considering the order of the objects.Since some opinions may be valid in a logic system but not in others,given any two logics,we can always count the number of the conflicting opinions between them(i.e.,valid in one logic but not in the other).Sometimes we will simply use d(L,P)to indicate the distance from a logic system to a profile P of logic systems,where P=(L1,...,Ln)and d(L,P)=
3.3 Three special kinds of merging operator
In the above,we have introduced our merging operator for a profile of logic systems.Normally,we aim to reach a common logic system after merging.However,sometimes with our merging method,the merged logic systems may not be unique.
Example 1.L0,L1,L2and L3are logic systems over the same language L={s1,s2,s3,s4},i.e.,

In other words,L0,L1,L2,and L3are all among the logic system list after merging.Therefore,we need to consider additional requirements to constrain further the behaviour of our merging operators,so that we can pick up the merging result that meets our needs.In the following,firstly we consider a merging operator,which is fair for all the cultural logic systems to be merged.
Definition 9(Impartial merging operator).Given a profile P=(L1,...,Ln)where each Li=is a cultural logic system,let d be a Hamming distance between two cultural logic systems.Suppose thatis the expansion of Liover P,and the resulted logic systems after merging by Definition 8 (i.e.,formula (8))areA merging operator,denoted as △im,for a profile logic systems is an impartial merging operator if it satisfies:
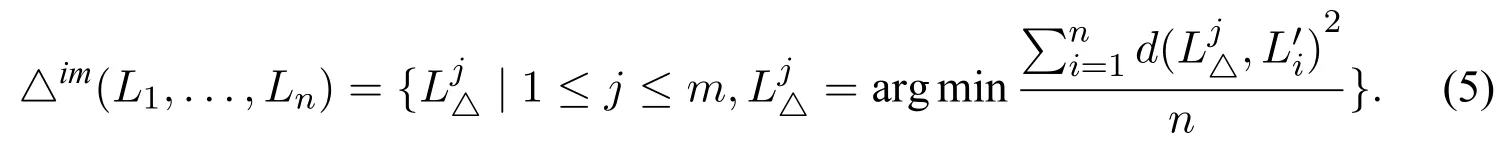
Intuitively,an impartial merging operator is fair because it selects the result that is not partial to any logic system in the expanded profile.
The following is an example of using impartial merging operator:

Example 2(Example 1 continued).Given the logic systems L1and L2as we mentioned in Example 1,and letSince obviously the resulted logic system using impartial merging operator are L0=L,Øand L3=(L,{(s1,s2)(s3,s4)}).
Secondly,we consider other two kinds of important merging operators:
Definition 10(Cautious merging operator).Given a profile P=(L1,...,Ln)where each Li=is a cultural logic system.The resulted logic systems after merging by Definition 8 (i.e.,formula (4))areA cautious merging operator,denoted as △c,is defined as:

The cautious merging operator reflects the fact that when the merging result is not unique,the logic system that includes the least valid opinions in it should be selected.On the contrary,the tolerant merging operator is the one with the most valid opinions in it.Formally,we have:
Definition 11(Tolerant merging operator).Given a profile P=(L1,...,Ln)where each Li=is a cultural logic system.The resulted logic systems after merging by Definition 8(i.e.,formula(4))areA tolerant merging operator,denoted as △t,is given by:

The following is an example of cautious merging operator and tolerant merging operator.
Example 3(Example 1 continued).Given the logic systems L1and L2as we mentioned in Example 1,and letSince

obviously the resulted logic system using the cautious merging operator is L0=(L,Ø)and the resulted logic system using the tolerant merging operator is L3=(L,{(s1,s2),(s3,s4)}).
4 Properties
In this section,we reveal some properties of our merging operator on cultural logic systems.Note in this section,we denote the consensual expansion for each logic system over P=and our merging operator as
Firstly,the resulted logic systems after merging are all consistent.Formally,we have:
Theorem 3(Consistency).Given a profile P=(L1,...,Ln),in which each Li=is consistent.
ProofWe need to prove that if there is an opinion(Σ,A) ∈then(Σ,¬A)suppose the number of the expanded logic systems which include(Σ,A)as a valid opinion is k(k ≥).Since the logic systems in the merging are all consistent,suppose the number of the expanded logic systems which include(Σ,¬A)as an valid opinion is h,then h <,by Definition 8,we know(Σ,¬A)□
The above property is reasonable because we are always aiming to reach consistent logic systems after merging.
The following property reflects that if there are no conflicts among the given profile,then the merged profile is simply the union of all the logic systems in the profile.
Theorem 4(Agreement).5See the proof in details in[17].Given a profile P=(L1,...,Ln)in which each Li=if no disagreements appear in P,i.e.,∀i,j ∈{1,...,n},∀(Σ,φ) ∈P(Li∩Lj)×(Li∩Lj),(Σ,φ)∈
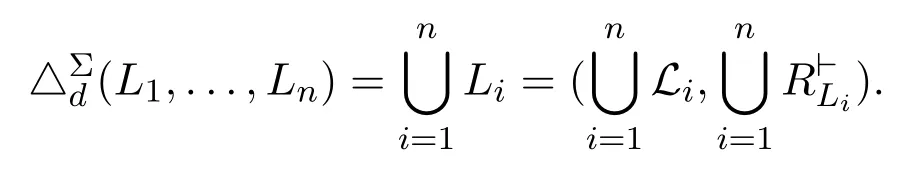
Now we turn to the next property,which reflects the intuition that if an opinion is not questioned by any of other agents,it should be collectively accepted.Formally,we have:
Theorem 5(Strong unanimity).6See the proof in details in[17].Given a profile P=(L1,...,Ln)in which eachbe the non-clash part of the profile.Then
The following property states that if an opinion is collectively acceptable in the merged result,then it must be valid in at least one of the cultural logic systems in a profile.
Theorem 6(Groundedness).7See the proof in details in[17].Given a profile P=(L1,...,Ln),for a merging oper-ator △,∀(Σ,φ) ∈then there exists at least one i ∈{1,...,n}such that
The following property means that a merged result should be independent of the merging order because all individual cultures equally important in the merging.
Theorem 7(Anonymity).8See the proof in details in[17].For any two profiles P=(L1,...,Ln) and P′=over L,which are permutations of each other,L is in the outcome after merging Piffit is also in the outcome after merging P′.
The following property states that if a cultural logic system is achieved simply by the majority vote on the opinions over the language,then this logic system is the output by using the merging operator we defined.Formally,we have:
Theorem 8(Majority preservation).Given a profile of logic system P=(L1,...,Ln) over the same language L,in which each Li=,a merging operatoris that we have defined in Definition 8.If a logic system LMajis obtained using the majority rule,9Several alternative definitions are possible for the majority rule in judgment aggregation when abstention is allowed.Here,for any(Σ,A)where Σ,A ∈L,one considers that the majority rule includes(Σ,A)as a valid opinion(resp.invalid opinion)when the number of logic systems which include(Σ,A)as a valid opinion(resp.invalid opinion)is strictly bigger than the number of logic systems that include(Σ,A)as a invalid opinion(resp.valid opinion),and it will do nothing otherwise.then ∀L△∈(L1,...,Ln),they share the same language and
ProofSuppose there is a logic system Lthere exists an opinion(Σ,A)over language L,(Σ,A)∈while(Σ,A)Then we can give another logic system L′based on L simply by adding(Σ,A)in it as a valid opinion.Since(Σ,A)∈the number of expanded logic systems which include(Σ,A)as a valid opinion is strictly bigger than the number of expanded logic systems which include(Σ,A)as an invalid opinion.Suppose there are k logic systems which include(Σ,A)as a valid opinion,it is obvious that k >By Definition 7,we have Thus,according to our merging method defined in Definition 8, LLn).Contradict.Therefore,∀L△∈they share the same language and□
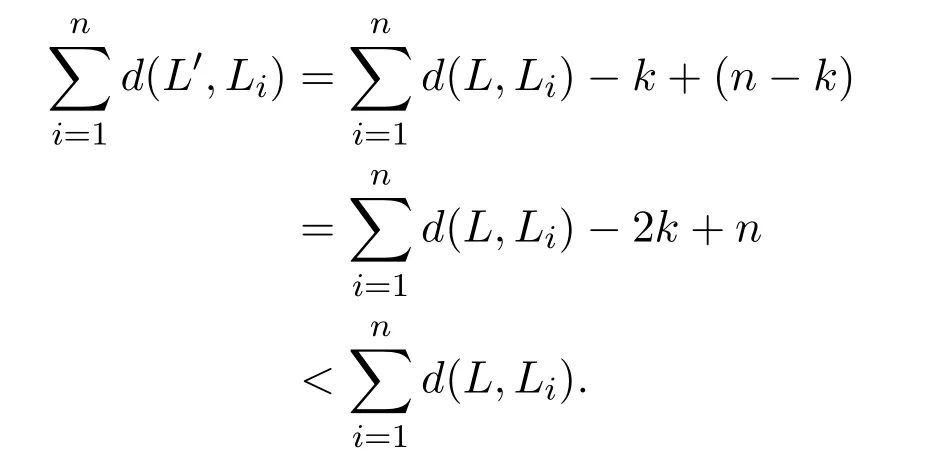
The following theorem states that if a cultural logic system is achieved simply by the majority vote on the opinions over the language,then it is exactly the merging result using our cautious merging operator on the opinions.Formally,we have:
Theorem 9(Uniqueness).Given a profile of logic systems P=(L1,...,Ln)over the same language L,in which each Li=let LMajbe the merged logic system obtained using the majority rule and let Lcbe the merged result by usting the cautious merging operator(see Definition 10),then LMaj=Lc.
ProofSince the logic systems in the profile share the same language L,then the language of Lcand LMajare the same,we just need to prove thati.e.,
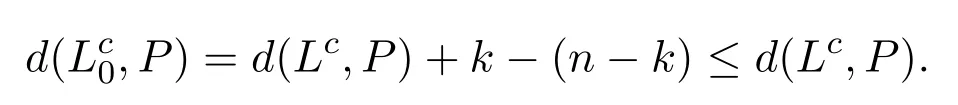
5 Discussion on Weighted Merging of Cultural Logic Systems
In the previous two sections,we study the problem of merging cultural logic systems with the same importance.However,in reality sometimes a certain cultural logic system may have a greater voice in merging.So,a weighted approach is required in this case.Moreover,all the pieces of opinions in a cultural logic system may not have the same importance,so weighted opinions should also be dealt with.Thus,in this section we will take the weight of each cultural logic system and each opinion in one cultural logic systems into consideration.Instead of giving new merging operators,we will revise the definitions of distance and aggregation function to fit in the situation where all sources are not equally important.
Firstly,we have:
Definition 12(Weight function).A weight function σ associated with an opinion o(or a cultural logic system L)is a total function that maps each o(or L)to a positive integer.
This definition of weight function is a measure of the importance of an opinion or a cultural logic system.Clearly,the greater the value is,the more important the opinion is in a cultural logic system(the more importance the cultural logic system is in a profile).This is in accordance with our intuitions.Notice that we assume the weight of an opinion or a cultural logic system is always given,as the valuation in classical proposition logic.When a weight is not given,we assume it is 1.
Based on the weight function we have defined above,we can introduce the concept of the weighted Hamming distance between two cultural logic systems as follows:
Definition 13(Weighted Hamming distance).Given two cultural logic systems L1and L2over the same language L,let σ1and σ2be weight functions for the opinions inThe weighted Hamming distance of L1and L2induced by σj(j ∈{1,2})is given by:

The following theorem means that our definition above is proper.
Theorem 10.The weighted Hamming distance holds the properties of non-negativity,identify of indiscernible,symmetry and triangular inequality we have mentioned in Theorem 2.
ProofLet Li=We check these properties one by one.
(i)Non-negativity:By Definition 13 and formula(13),d(Li,Lj)≥0 is obvious.
(ii)Identity of indiscernible:The proof is similar to that given in the proof of Theorem 2(ii).
(iii)Symmetry:The proof is similar to that give in the proof of Theorem 2(iii).
(iv)Triangular inequality:We define the conflict part of two logic systems Liand Ljas the set of opinions on which the two logic systems differ,i.e.,
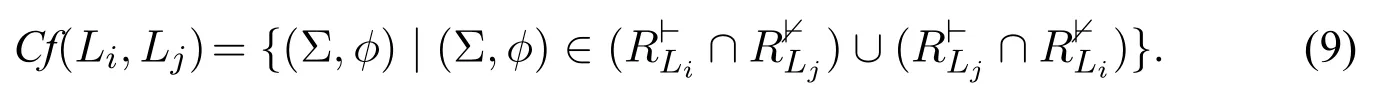
We can see that d(Li,Lj)= |Cf(Li,Lj)|.Suppose d(Li,Lj)= l1,d(Lj,Lk)= l2and d(Li,Lk)=l3,by Theorem 2,we have l3≤l1+l2.Actually,∀o ∈Cf(Li,Lk),it is always that o ∈Cf(Li,Lj)or o ∈Cf(Lj,Lk).By Definition 13,we have
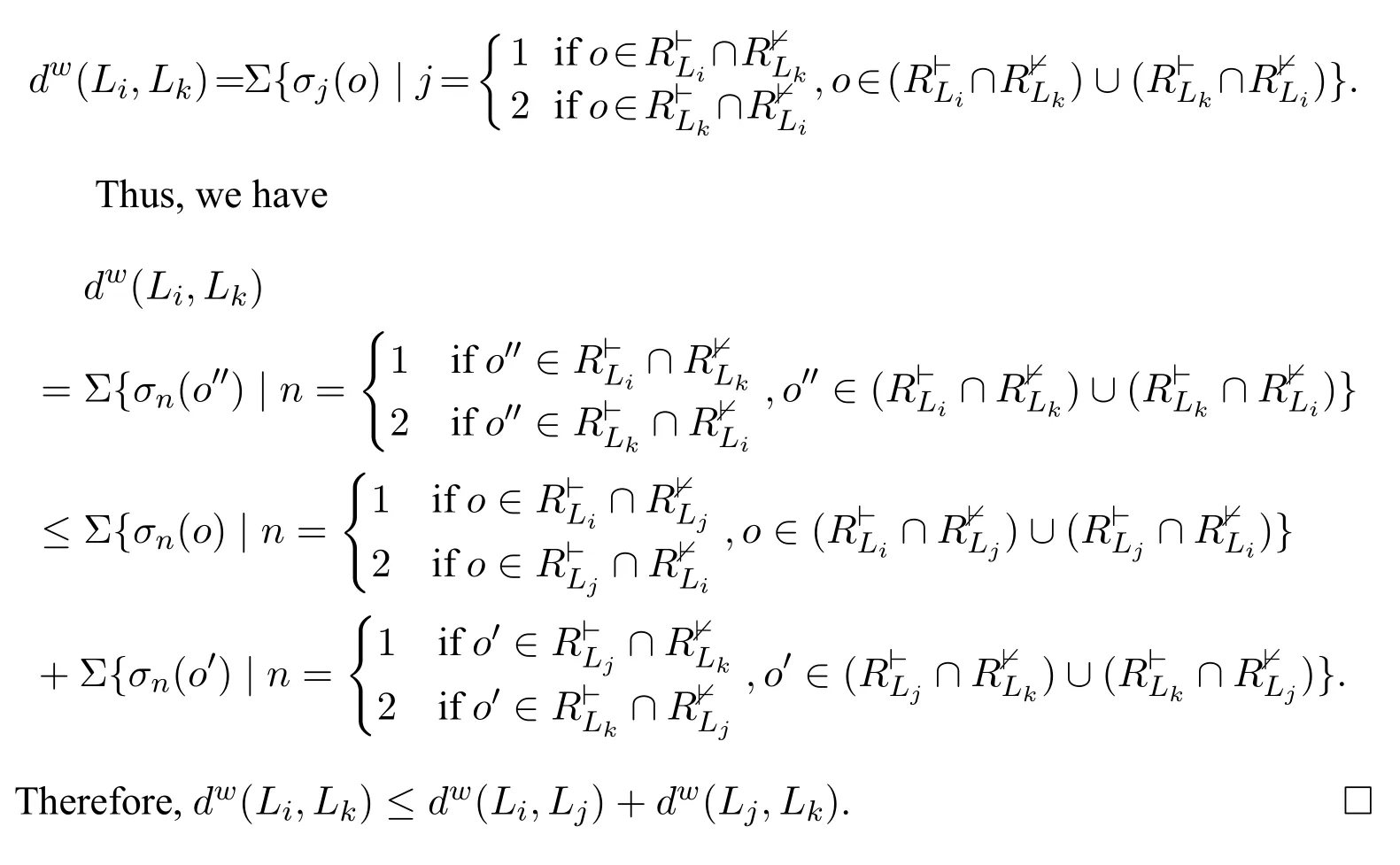
Definition 14(Hamming distance between cultural logic systems).Given two cultural logic systems L1and L2over the same language L,their Hamming distance is the number of opinions on which the two logic systems differ,i.e.,
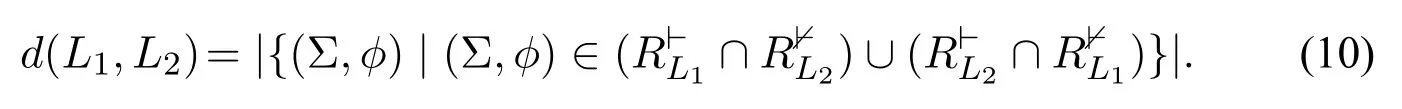
In the following,we will define the aggregation function that are used when the cultural logic systems do not have the same importance.
Definition 15(Weighted sum).Given a profile P=(L1,...,Ln),where each Li=and the weighted function of each cultural logic system Liis σi.Let L=be a logic system and dw(L,Li)be the weighted Hamming distance between L and Li(1 ≤i ≤n)then the weighted sum aggregation function induced by σiis a function from 2N+to N+(N+is the positive integer set)defined as:
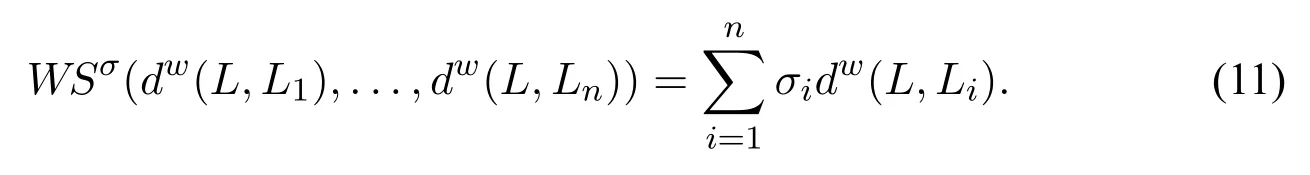
In the following we give an example:
Example 4.Suppose American Amy(A),Russian Blair(B),and Chinese Chris(C)have a brief conversation about the cultural phenomena of their own countries.In Amy’s opinion,the sentence of “Where are you going?” (s1)is an invasion upon privacy(s2),and she thinks“Dragon(s3)symbolises evil(s4)”;while for Chris,she does not think the question has any thing to do with the privacy issue,and thinks that dragon could not symbolise evil.At last,Blair agrees with Amy on the privacy issue but agree with Chris on the dragon.In addition,they have different importance degrees.Amy is the most important one.In particular,the weight of her cultural logic system is σ(LA)=3,while σ(LB)= σ(LC)=1.In addition,Amy thinks that the opinion of “Dragon(s3)symbolised evil (s4)” is much more reliable than other opinions.Specifically,the weight of this opinion is σ(s3,s4)=3 while Blair and Chris take all their opinions with the same reliability.
We first expand their logic systems to the same language L′with the consensual expansion,then based on language L′={s1,s2,s3,s4},there are in total 260different logic systems by taking different numbers of opinions as valid opinions.
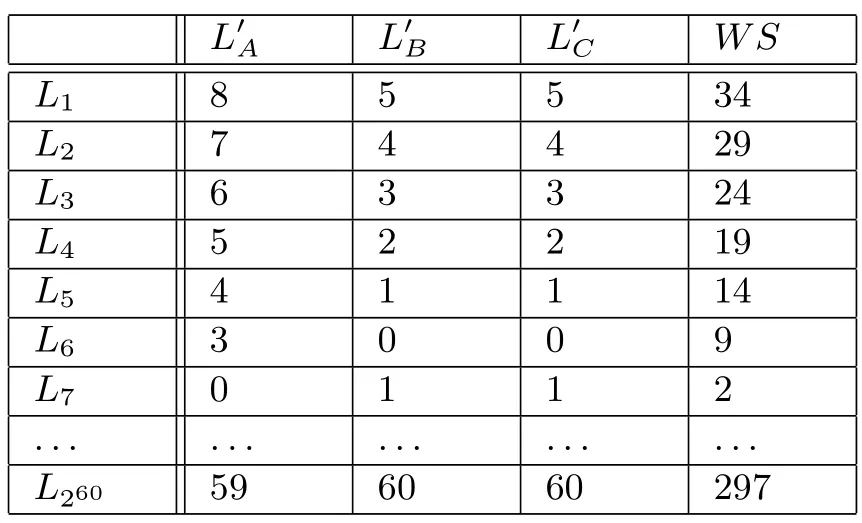
Table 1:Weight Hamming Distances with WS
We summarise the calculations in Table 1.For each possible logic system generated over languages L′= {s1,s2,s3,s4},we give the distance between this logic system and the expanded logic systems for Amy,Blair,and Chris using our weighted Hamming distance measure in Definition 12 and the weighted sum of them.By using our weighted sum aggregation function,we can obtain the total distance from one logic system to the profile.10In Table 1,for example,the weighted Hamming distance between L1 and is 8,and the weighted sum of weighted Hamming distance is 3×8+5+5=34.Putting all the information together,we find that the result of merging the weighted cultural logic systems of Amy,Blair,and Chris is:

6 Related Work
In this section,we will compare our study with some existing ones which concerns how to fuse logic based information.
6.1 Propositional belief merging
Propositional belief merging has received much attention for the past two decades.A number of belief merging operators have been defined and investigated so far from a logical standpoint,and an important subset of propositional merging operators consists of the distance-based operators.([21,34,35])For such operators,the models of the merged base are precisely the models of the integrity constraint which are at a minimal distance of the input profile.Also a lot of studies extend the framework of logic-based merging introduced above in different ways.([28,19,11,8])For example,Konieczny,Lagniez,and Marquis([19])focus on the computational aspects of propositional belief merging.They present encoding schemes for distance-based belief merging operators relying on the (possibly weighted)drastic distance or the Hamming distance between interpretations,and using sum,GMax(leximax)or GMin(leximin)as aggregation function.
There are several similarities between the above studies and the merging of our cultural logic system.Nevertheless,there are three significant differences between theirs and ours.Firstly,the merging of belief systems is supposed to be under the same cultural background,while our work considers the merging of cultural logic systems in different cultures.As a result,the cultural logic system that we defined in this paper emphasises the plurality of logic system,while the merging theories above do not put it into consideration.Secondly,the representation language of our framework is a binary relation structure other than the propositional logic in belief merging theories,which is more suitable to reflect different opinions on the same thing.Thirdly,we reveal a number of properties(i.e.,consistency,agreement,strong unanimity,groundedness,anonymity,majority preservation,and uniqueness),while in the above work they did not discuss these properties.Hence,our framework of merging cultural logic systems may benefit the research in their topics as well.
6.2 Merging argumentation systems
Some researchers investigate how to merge argumentation systems.For example,Coste-Marquis et al.([7])present a general framework for merging argumentation systems from Dung’s theory of argumentation ([9]).The merging argumentation systems is under the same cultural background,while our merging of cultural logic systems is concerned with different cultures.Moreover,although the argument framework is also a pair,it is totally different from ours.Actually,its binary relation is an attack relation,while that in our cultural logic system is an implication relation,indicating that a sentence could be reached as a conclusion from a set of premises.
6.3 Judgment aggregation
Judgment aggregation is about how to aggregate individual judgments on logically interconnected propositions into a collective decision on the same proposition.([22])So,it is also a merging process of information from different sources.For example,the logic aggregation theory([41])is closely related to our work.More specifically,their logic aggregation is treated as argument-wise,and some possibilities and impossibilities of aggregating logics are studied.Moreover,they prove that certain logical properties can be preserved by some desired aggregation functions,while some of other logical properties cannot be preserved together under nondegenerating aggregation functions,as long as some specific conditions are met.Their work aims to investigate under which conditions aggregation functions satisfy certain logical properties.Nonetheless,the purpose of our work is to investigate how to apply the distance-based merging operator into logic systems with binary relation that well reflects different opinions on the same thing in different cultures.Thus,we propose a particular merging framework in intercultural environments,which satisfies a set of logical properties.
6.4 Weighted merging
Some researchers studied the weighted approaches in belief merging and argument system merging(see[35]for a survey).For example,Dubois,Kaci,and Prade([5])present a general approach for fusing prioritised propositional information,in which priorities are represented in the possibilistic logic framework.Nevertheless,what they merged are beliefs which are represented simply as propositions,while the cultural logic systems in our work are two-tuple structures.Accordingly,our weighted merging method is obviously different from theirs.
Although in their work an argument system is also a two-tuple structure,there are some significant differences between their approach and ours.Firstly,their merging method focused on defining the weight of attack relations of the arguments in an argument system.However,in our merging approach,what we concern is the weight of each cultural logic system and the weight of each valid opinion in certain cultural logic systems,but think that the inference relations between sentences are decided.Secondly,the merged result of their approach is a weighted argument system emphasising the weight of attack relations between the arguments,while the outcome of our method is simply a set of valid opinions.
6.5 Logic system combination
Also many studies concern the general definition and combination of logic systems.([33,31,32])For example,[33]gives general definitions of logical frameworks and logics,and then general definitions for equivalence of logics,translation between logics,and combination of logics.They also establish general criteria for the soundness and completeness of these logic systems.Both their work and ours are concerned with logic systems using approaches independent of the specific logical framework.However,our work is quite different from theirs.Firstly,they define logic systems using a formalist approach,while we adopt an abstract one.Roughly speaking,the former explicitly represents the syntax and proof theory,whereas the latter assumes abstract sets of sentences and consequence relations.Secondly,they formulated logic systems systematically as logical theories,while we represent a logic system simply as a binary relation and use the distance-based merging method to get a coherent logic system.Thirdly,their study is irrelevant to culture,while ours focus on cultural opinion merging.
7 Conclusion
The resolution of cultural conflicts is a very important issue worldwide.To this end,this paper presents a method for merging cultural logic systems.More specifically,we define each agent’s cultural logic system as a tuple of the language and a binary relation over the language,which reflects well different opinions on the same thing in different cultures.Then merging different systems of this kind is a two-step process.Firstly,all the logic systems are expanded to be based on the same language;and then a distance-based method is used to select a logic system that is the nearest to the expanded one from the given profile of cultural logic systems.In this work,we employ the Hamming distance to measure the distance between any two cultural logical systems,and we define three special merging operators:impartial merging operator,cautious operator,and tolerant merging operator.Moreover,we reveal that our merging operators possess some good properties such as consistency,agreement,disagreement,strong unanimity,groundedness,anonymity,majority preservation,and uniqueness.In addition,we also discuss how to merge cultural logic systems with different degrees of importance and with opinions which are important differently.Our resolution to intercultural conflict can be used as the basis for agents from different cultures to communicate with each other,and benefit governments in making their immigration policies.
There are several things worthy doing in the future.First,with our merging operator,the merged logic systems may not be unique.If a particular one among them is required,a choice function needs to be designed.Second,besides distance-base merging methods,other merging operators (such as disjunctive operators,conflictbased operators,and default-based operators)may be used to merge cultural logic systems.If so,it is also interesting to examine their differences.Third,as we have seen,given a certain language,because the number of opinions and cultural logic systems that could be generated over the language grow exponentially,the computation complexity of the distance calculation is very higher.Therefore,a new method for cultural logic system merging,which can significantly reduce the computation complexity,is required.Fourth,it is also interesting to integrate our merging method with negotiation methods([18,23])to resolve cultural conflicts.Finally,our work in the paper actually is a method for resolve opinion conflicts.Maybe it is worth integrating our method with opinion mining methods([4,37,43,42]),so that computer systems not only can mine out different opinions from social media but also can merge them to resolve potential conflicts among them.
杂志排行
逻辑学研究的其它文章
- Analytical Research on the Expression of Argumentative Discourse from the Perspective of Generalized Argumentation—In the Example of Jack Ma’s Verbal Advocacy of 996 Work System*
- Reconstructive Deductivism and Its Misapplication
- Privacy in Arrow Update Logic*
- On Dimensions,Standard Part Maps,and p-Adically Closed Fields*
- Comparing Fixed-Point and Revision Theories of Truth from the Perspective of Paradoxicality*
- A New Way of Defining Deductive Consequence for Modal and Predicate Logic
