Privacy in Arrow Update Logic*

2020-12-24YanjunLi

逻辑学研究 2020年6期

Yanjun Li

Abstract. Arrow Update Logic is a theory of epistemic access elimination that can be used to reason about multi-agent belief change.In Arrow Update Logic,it is common knowledge among agents how each will process incoming information.This paper develops the basic theory of Arrow Update Logic to deal with private announcements.In this framework,the information is private for an agent group.Moreover,this paper proposes a labelled tableau calculus for this logic and also shows that this logic is decidable.

1 Introduction

Information plays an important role in several fields of scientific research,such as philosophy,game theory,and artificial intelligence.In this paper,the notion of information is confined to the kind of information in one’s mind,which can also be called belief or knowledge.In real-life contexts,information is often communicated.This leads to a change of agents’information without any change in the bare facts of the world.One kind of these communicative events is announcements.This paper will focus on reasoning about information change due to announcements.

In a multi-agent system,there are at least three types of announcements:public,private and semi-private (cf.[3]).Imagine a scenario where two agents a1and a2are in a room,and in front of them,there is a coin in a closed box.Neither of them knows whether the coin is lying heads up or tails up.A public announcement occurs when the box is opened for both to see.This changes not only the agent’s information about the bare facts(basic information)but also agents’information about each other(higher-order information).When a1secretly opens the box and a2does not suspect that anything happened,the effect is the same as the effect that the truth is privately announced to a1.This changes only a1’s basic and higher-order information.A semiprivate announcement occurs when a1opens the box and a2observes a1’s action but a2does not see the coin.This changes a1’s basic information and the higher-order information of both.Please note that a public announcement can be seen as a special private announcement,i.e.,an announcement which is privately announced to the whole group.

Plaza([17])develops a logic that is concerned with information change by public announcements,in which a public announcement of a statement eliminates all epistemic possibilities in which the statement does not hold.Gerbrandy and Groeneveld([12])propose a more general dynamic epistemic logic for information update,where a private announcement for an agent group G is an update that is conscious only for G.The dynamic epistemic logic with action models(DEL,[3,4])can formalize a wide range of information change.An action model is a Kripke model-like object that describes agents’beliefs about incoming information.The logic LCC([5])can model information communication that is partial observation,and a private announcement for G is a piece of information whispered to G([7]).Logics introduced in[8,6]can model information change based on attentions,and an announcement is private for agents who are paying attention when the announcement is made.Private announcements can also be modeled in [11].The precise method by which private announcements are dealt with in these logics are different due to their different motivations,but they share the same feature that the basic model will be expanded when a private announcement happens.

Kooi and Renne’s Arrow Update Logic(AUL,[13])can also formalize reasoning about information change produced by public and semi-private announcements.Different from other logical frameworks,AUL models information change by updating the epistemic access relation,without changing the domain of the model.However,in AUL,it is common knowledge among agents how each will process incoming information.This assumption of common update policy is dropped in its extension,Generalized Arrow Update Logic(GAUL,[14]),which can capture the same information change that can be modeled in DEL.

Although DEL and GAUL are much more expressive than AUL,the great expressive power does not come for free.Their update operators are much more complex than the update operator of AUL.This paper presents a variation of AUL,Private Arrow Update Logic(PAUL),which also drops the common update-policy assumption of AUL(so that private announcements can be expressed)and keeps the update operator as simple and intuitive as in AUL.In our framework,each information update is visible only for a group of agents,so private announcements can be dealt with.This logic framework is also inspired by the context-indexed semantics developed in[18]and[20].As we will see,PAUL can formalize reasoning about information change due to public,private and semi-private announcements.Our logic is more general than AUL in the sense that each information update in AUL can be seen as update that is visible for all agents in our framework.Our logic can also be seen as a fragment of DEL,and there are information change,such as lying,cannot be expressed in our framework.

The rest of this paper is organized as follows:Section 2 proposes the language and semantics of PAUL,and works out some examples;Section 3 presents the tableau calculus for PAUL and show soundness and completeness;Section 4 shows PAUL is decidable;Section 5 concludes with some directions for further research.

2 The Logic PAUL

2.1 Syntax and semantics

In this section,we introduce the language and semantics of this logic.

Definition 1(PAUL Language).LetAgtbe a nonempty finite set of agents,and letPbe a countable set of atomic propositions.The PAUL language is generated by the following BNF:

where p ∈P,a ∈Agtand G ⊆Agtis a superset of the set of agents occurring in U.

We will often omit parentheses around expressions when doing so ought not cause confusion.The expression φ is called a PAUL-formula(or just formula).The expression [U,G]occurring in a formula is called a PAUL-update (or just update),which consists of an update core U and an agent group G to which the update is visible.We let LPAULdenote the set of formulas.Given formulas φ and ψ and an agent a ∈Agt,the syntactic object(φ,a,ψ) ∈U is called an a-arrow specification.As usual,we use the following abbreviations: ⊥:=¬⊤,φ∨ψ :=¬(¬φ∧¬ψ),φψ :=¬φ ∨ψ,◇aφ:=¬□a¬φ.Moreover,if there is only one arrow specification in U,we write[{(φ,a,ψ)},G]as[(φ,a,ψ),G].Similarly,we write[U,{a}]as[U,a].

Intuitively,the formula □aφ expresses that agent a believes φ.The formula[U,G]φ expresses that φ holds after the arrow update[U,G].The update[U,G]means that the update is visible only to agents in G.Please note that the update in AUL has only one part,that is[U],which is visible for all agents.Therefore,the update[U]in AUL is the same as the update[U,Agt]here.

Definition 2(Kripke Model).A Kripke model M is a tupleWM,RM,VM,consisting of a nonempty set WMof worlds,a function RMassigning each agent a ∈Agta binary relation⊆WM×WM,and a function VM:PP(WM).A pointed Kripke model is a pair(M,s)consisting of a Kripke model M and a world s ∈WM;the world s is called the point of(M,s).

Given a Kripke model M,we call WMthe domain of the model.For each agent a ∈Agt,we calla’s possibility relation since it defines what worlds agent a considers possible in any given world.Please note that updates considered in this paper do not change any bare facts but only the agent’s beliefs.Therefore,when an update happens,we do not have to change the domain of the model but only change the possibility relations(or‘arrows’).

Definition 3.Let ρ=[U1,G1]···[Un,Gn]be an update sequence(or just sequence),and ρ= ϵ if n=0.The update sequence ρ|ais defined by the following induction on n.

In the following text,we will always use symbols ρ,ρ′,ρ[U,G],ρ′[U,G]to denote sequences of updates.The sequence ρ|ameans that the updates are visible to the agent a.

Definition 4(PAUL Semantics).Given a pointed Kripke model (M,s),an update sequence ρ and a formula φ,we write M,s ⊨ρφ to mean that φ is true at M,s after updates ρ,and we write M,s ⊭ρφ for the negation of M,s ⊨ρφ.The relation(notation:⊨ρ)is defined by the following induction on formula construction.

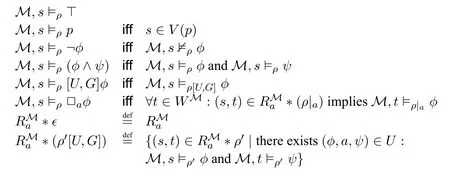
We also write M,s ⊨ϵφ as M,s ⊨φ.To say that a formula φ is valid,written as ⊨φ,means that M,s ⊨φ for each pointed Kripke model(M,s).The negation of ⊨φ is written as ⊭φ.To say that a formula φ is satisfiable means there exists a pointed model(M,s)such that M,s ⊨φ.

Kooi and Renne([13])present an axiomatic theory for AUL,in which the most important axiom states that an agent’s belief after an update can be reduced to his(her)belief before the update.The following proposition shows that the PAUL version of this reduction axiom also holds.

Proposition 5.

ProofLet (M,s)be a pointed Kripke model.Firstly,we show that if M,s ⊨[U,G]□aφ then M,s∧Assume that M,s ⊨[U,G]□aφ and(ψ,a,χ) ∈U,we will show that M,s ⊨ψ□a(χ[U,G]φ).Let M,s ⊨ψ and t be a state such that(s,t) ∈We only need to show that if M,t ⊨χ then M,t ⊨[U,G]φ.If M,t ⊨χ,since M,s ⊨ψ and(ψ,a,χ)∈U,this follows that(s,t) ∈Since a ∈G,we have that[U,G]|a=[U,G].Thus,we have(s,t) ∈Moreover,since M,s ⊨[U,G]□aφ,this follows that M,t ⊨[U,G]φ.Therefore,we have that M,t ⊨[U,G]φ.

Secondly,we show that if M,sthen M,s ⊨[U,G]□aφ.Assume that M,s ⊭[U,G]□aφ.It follows that there exists t ∈WMsuch that(s,t)∈*[U,G]and M,tSince(s,t)∈*[U,G],it follows that (s,t) ∈and there exists (ψ,a,χ) ∈U such that M,s ⊨ψ and M,t ⊨χ.Moreover,since M,swe then have M,t ⊨[U,G]φ,namely M,t ⊨[U,G]φ.This is in contradiction with M,t ⊭[U,G]φ.Therefore,we have if M,sthen M,s ⊨[U,G]□aφ.□

The following proposition shows that if an update is not visible for an agent,then her belief after the update is the same as her belief before the update.

Proposition 6.⊨[U,G]□aφ ↔□aφ if a∉G.

ProofWe have the following:

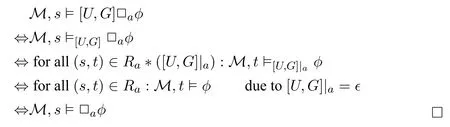
We know that the replacement of equivalents plays an important role in equivalently reducing an AUL formula to a formula with out updates.Next,we will show that the replacement of equivalents also holds in PAUL.Before that,we first show the the following proposition.

Proposition 7.Let ρ be a sequence of updates and (M,s) be a pointed model.We then have that M,s ⊨ρφiffM′,s ⊨φ for each φ ∈LPAUL,where M′=WM,R′,VMand R′=

ProofWe prove it by induction on φ.We only focus on the case of [U,G]φ; the other cases are straightforward by IH.

We need to show that M,s ⊨ρ[U,G]φiffM′,s ⊨[U,G]φ.Please note thatLet M′′=WM,R′′,VMwhere R′′=a ∈Agt}.By IH,we have that M,s ⊨ρ[U,G]φiffM′′,s ⊨φ.What is more,by IH,we also have that M′,s ⊨[U,G]φiffM′′,s ⊨φ.Therefore,we have the following:

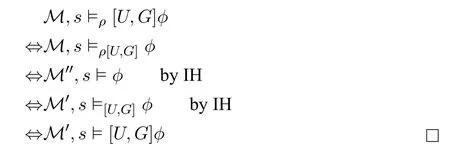
Please note that,by the proposition above,we have that,for any update sequence ρ,⊨ρφ if ⊨φ.Therefore,we have the general version of Propositions 5 and 6:

Now we are ready to prove the replacement of equivalents.

Proposition 8.Let φ′be the result of replacing some occurrences of ψ in φ by ψ′1Here we confine the occurrence of ψ in φ on the occurrence that ψ is not in an update.In the following,we will see that this confined version of replacement of equivalents is sufficient to show the reduction theorem..We then have that ⊨φ ↔φ′if ⊨ψ ↔ψ′.

ProofWe prove it by induction on φ.We only focus on the case of [U,G]φ; the other cases are straightforward by IH.

We need to show that M,s ⊨[U,G]φiffM,s ⊨[U,G]φ′.Let the model M′beWM,R′,VMand R′=We then have that M,s ⊨[U,G]φiffM,s ⊨[U,G]φ,and by Proposition 7 we have that M,s ⊨[U,G]φiffM′,s ⊨φ.By IH,we then have that M′,s ⊨φiffM′,s ⊨φ′.Then,by Proposition 7 again,we have that M′,s ⊨φ′iffM,s ⊨[U,G]φ′. □

Next,we will show that each formula in PAUL can be equivalently reduced to be a formula with out updates.

Theorem 9.For each formula φ,there is a formula φ′such that ⊨φ ↔φ′and there are no updates in φ′.

ProofWe first define the translation function t as follows:

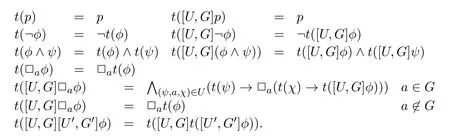
By induction on φ,we will show that ⊨φ ↔t(φ)and that there are no updates occurring in t(φ).We then only focus on the case of [U,G]φ; the other cases are straightforward by IH.

To show that ⊨[U,G]φ ↔t([U,G]φ)and that there are no updates occurring in t([U,G]φ),we continue to do induction on φ.

· [U,G]p.It is obvious.

· [U,G]¬φ.By semantics,we have that ⊨[U,G]¬φ ↔¬[U,G]φ.By IH,we have that ⊨[U,G]φ ↔t([U,G]φ)and that there are no updates occurring in t([U,G]φ).Thus,we have that ⊨¬[U,G]φ ↔¬t([U,G]φ)and that there are no updates in¬t([U,G]φ).

· [U,G](φ ∧ψ).Since ⊨[U,G](φ ∧ψ)↔[U,G]φ ∧[U,G]ψ by semantics,it is straightforward by IH.

· [U,G]□aφ and a ∈G.By Proposition 5,we only need to show that,for each (ψ,a,χ) ∈U,⊨(ψ□a(χ[U,G]φ)) ↔(t(ψ)□a(t(χ)t([U,G]φ)))and there are no updates in t(ψ), t(χ),or t([U,G]φ).These are straightforward by IH.

· [U,G]□aφ and a∉G.By Proposition 6,we only need to show that □aφ can be equivalently reduced to be a formula with out updates.By IH,we have that⊨φ ↔t(φ)and there are no updates in t(φ).Thus,we have that ⊨□aφ ↔□at(φ)by Proposition 8.

· [U,G][U′,G′]φ.We need to show that ⊨[U,G][U′,G′]φ↔t([U,G]t([U′,G′]φ))and that there are no updates in t([U,G]t([U′,G′]φ)).By IH,we have that there is some formula φ′= t([U′,G′]φ)such that ⊨[U′,G′]φ ↔φ′and that there are no updates in φ′.By IH again,we have that ⊨[U,G]φ′↔t([U,G]φ′)and there are no updates in t([U,G]φ′).Since ⊨[U′,G′]φ ↔φ′,by Proposition 8,we then have that ⊨[U,G][U′,G′]φ ↔t([U,G]φ′). □

2.2 Announcements in PAUL

In this section,we will show how public,private and semi-private announcements are captured in PAUL.Let us consider the following scenario of a concealed coin,which is a tweaked version of an example used in[3].

Example 10(Basic scenario).Two agents a1and a2enter a large room which contains a remote-controlled mechanical coin flipper.One of them presses a button,and the coin spins through the air and lands in a small box on a table with heads or tails lying up.The box is closed and they are too far away to see the coin.

Figure 1:the basic model M

Just as in[3],this can be modelled by a Kripke model M,which is pictured in Figure 1.The possible world H ∈WMrepresents the possible fact that the coin is lying heads up,and T ∈WMrepresents tails up.The proposition p means that the coin is lying heads up,so it is only true in H.The possibility relations of a1and a2indicate that both of them do not know whether the coin is lying heads or tails up.

Example 11(Public announcement).After the basic scenario,one of them opens the box and puts the coin on the table for both to see.The effect of this event on their beliefs is the same as that of a truthful statement publicly announced to them that the coin is lying heads or tails up.

Figure 2:The possibility relations after the update[U1,G1]

After the truthful announcement that the coin is lying heads or tails up,both of them think there is only one possibility in any given world.Thus only their epistemic accesses to any given world should be preserved.This announcement is visible for both,since it is publicly announced.Therefore,this public announcement can be captured by [U1,G1]where U1= {(p,a1,p),(¬p,a1,¬p),(p,a2,p),(¬p,a2,¬p)}and G1= {a1,a2}.After the update [U1,G1],the possibility relations of a1and a2turn out to be the same,as shown in Figure 2.Moreover,since the update is visible to both of them, a1’s possibility relation in a2’s opinion is the same as a1’s real possibility relation,namelyIf H is the actual world,after this public and truthful announcement,both of them believe that the coin is lying heads up and that the other also believes so.We can check the following formulas.

· M,H ⊨[U1,G1](□a1p ∧□a2p)

· M,H ⊨[U1,G1](□a1□a2p ∧□a2□a1p)

More generally,public announcements of the truth value of φ can be expressed in our framework by the update[U,Agt]where U={(φ,a,φ),(¬φ,a¬φ)|a ∈Agt}.Therefore,public announcement logic is a fragment of PAUL.

Example 12(Private announcement).After the basic scenario of Example 10,agent a1secretly opens the box herself.Agent a2does not observe that a1opens the box,and indeed a1is certain that a2does not suspect that anything happened.The effect of this on their beliefs is the same as secretly and privately announcing the truth to a1.

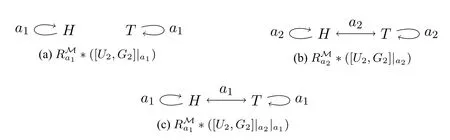
Figure 3:The possibility relations after the update[U2,G2]

After the truth is announced to a1,she thinks that there is only one possibility from any given world.Thus a1’s epistemic accesses to the world itself should be preserved after the announcement.Since the announcement is secret and private,it is visible only to a1.This private and truthful announcement can be captured by the update[U2,G2]which is defined as U2={(p,a1,p),(¬p,a1,¬p)}and G2={a1}.

After the update[U2,G2],a1’s possibility relation(Figure 3a)will change,but a2’s possibility relation(Figure 3b)will remain the same as before.Moreover,since a2does not suspect that anything happened,a1’s possibility relation in a2’s opinion(Figure 3c)does not change at all after the announcement.After this private and truthful announcement to a1,only a1believes the truth while nothing happened to a2’s beliefs.We can check the following formulas.

· M,H ⊨[U2,G2](□a1p ∧¬□a2p)

· M,H ⊨[U2,G2]¬□a2(□a1p ∨□a1¬p)

More generally,a private announcement of the truth value of φ to a group of agents G ⊆Agtcan be expressed in our framework by the update [U,G]where U={(φ,a,φ),(¬φ,a,¬φ)|a ∈G}.Our logic is a fragment of DEL,since there is certain information change,such as lying,that can not be expressed in PAUL but can be modeled in DEL.

Figure 4:The possibility relations after the update[U3,G3]

Example 13(Semi-private announcement).After the basic scenario of Example 10,agent a1opens the box herself.Agent a2observes that a1opens the box but does not see the coin.Agent a1also does not disclose whether it is heads or tails.The effect of this on their beliefs is the same as a semi-private announcement to a1,which means that the truth is announced to a1only,but a2notices what happened.

Since the truth is announced to a1,she will know the truth after the announcement.The situation of a2is a little complex.Firstly, a2’s possibility relation will remain the same as before since a2is not announced the truth.Secondly,a1’s possibility relation in a2’s opinion will change since he observed that a1is announced the truth.This semi-private announcement can be captured by the update[U3,G3]which is defined as U3={(p,a1,p),(¬p,a1,¬p),(⊤,a2,⊤)}and G3={a1,a2}.

Agent a1’s possibility relation(Figure 4a)will change to the reflexive relation after the update.Since the announcement is not disclosed to a2, a2’s possibility relation (Figure 4b)will not change after the update.However,after the update, a1’s possibility relation in a2’s opinion (Figure 4c)will change because a2observes the announcement.After the announcement, a2believes that a1believes the truth,but a2still could not distinguish between the fact that a1believes p and the fact that a1believes¬p.We can check the following formulas.

· M,H ⊨[U3,G3](□a1p ∧¬□a2p)

· M,H ⊨[U3,G3]□a2(□a1p ∨□a1¬p)

More generally,each semi-private announcement of the truth value of φ to a group of agents G ⊆Agtcan be expressed in our framework by the update[U,Agt]where U= {(φ,a,φ),(¬φ,a,¬φ),(⊤,b,⊤) | a ∈G,b ∈AgtG}.Each update in AUL is a semi-private announcement in nature,since all updates in AUL is visible to all agents.Therefore,each formula φ in AUL can be equivalently transformed to a formula in PAUL by replacing each update [U]in φ with [U,Agt].So,AUL is a fragment of PAUL.

3 Tableau Method

This section will present a proof method for PAUL that uses analytic tableaux.As a typical tableau method,given a formula φ,it systematically tries to construct a model for it.When it fails,φ is inconsistent and thus its negation is valid.

The tableau method in this paper will manipulate tableau terms,which consist of two parts:the first part is an update sequence;the second part is a formula,or a check mark,or a cross mark.In addition,each term is prefixed by a label which stands for a possible world in the model under construction.A similar method is used in[1,2,10,16].

Definition 14(Term).A term (or tableau term)is a pair (ρ,x)where ρ is a finite update sequence[U1,G1]···[Un,Gn](ρ= ϵ if n=0)and x is a check mark√,a cross mark✘or a formula φ ∈LPAUL.

Definition 15(Labelled term).A label is an alternating sequence of integers and agents,namely σ ::= n | σan where n ∈N and a ∈Agt.A labelled term is a pair consisting of a label and a term,and we also write it as a tripleσ,ρ,x.

In the following text,we will always use symbols σ,σ′,σan to denote labels.Each label represents a possible world in a Kripke model.Moreover,a label σan occurring on a branch of a tableau also indicates that there is an a-arrow from the possible world σ to the possible world σan.A labelled termσ,ρ,φmeans φ is true at the possible world σ after the announcement sequence ρ.A labelled termσan,ρ,√means the a-arrow from σ to σan is preserved after the update sequence ρ.Conversely,a labelled termσan,ρ,✘means the a-arrow is not preserved.

Definition 16(Branch).A branch is a set of labelled terms.A label σ is new in a branch b if there is no term in b that is labelled with σ.

In the following text,we will always use b,b′,b1,··· to denote branches and B to denote a set of branches.

Definition 17(Tableau).A tableau T for φ0∈LPAULis a set of branches inductively defined as follows.

· Let T′be a tableau for φ0and b be a branch in T′.If B is a finite set of branches generated by applying one of the tableau rules in Table 1 on b(for instance,let b= {σ,ρ,¬(φ ∧ψ)}then B= {b ∪{σ,ρ,¬φ},b ∪{σ,ρ,¬ψ}}),then the set(T′{b})∪B is a tableau for φ0.

Rules(¬¬),(¬∧)and(∧)are exactly as for propositional logic.Rules(¬□a)and □aare different from their counterparts commonly used in tableau calculi for normal modal logic.The intuition behind Rule (¬□a)is that if the possible world that σ stands for satisfied¬□aφ after the update sequence ρ then it needs to satisfy the following conditions:there exists a possible world that is represented by σan(the form of σan indicates that there is an a-arrow from σ to σan);σan,ρ|a,√means the a-arrow from σ to σan will be preserved after the update sequence ρ|a;σan,ρ|a,¬φmeans ¬φ is true in σan after the update sequence ρ|a.Similarly,Rule(□a)means that □aφ is true in σ after ρ if and only if for each possible world that is accessible by a-arrow from σ:either the a-arrow is removed after ρ|a,or φ is true in it after ρ|a.

Rule (¬[U,G])and Rule ([U,G])reflect the feature of the semantics that the updates are just remembered and they are used to update the possibility relation only when □aformulas are evaluated.Rule(√1)means that the a-arrow is preserved after ρ[U,G]if and only if it is firstly preserved after ρ and then preserved by some a-arrow specification in U.Rule(√2)says it is not possible that the a-arrow from σ to σan is preserved after ρ[U,G]if there are no a-arrow specifications in U.Rule(✘1)and Rule(✘2)specify the conditions under which the a-arrow from σ to σan will be removed.It is removed after ρ[(ψ,a,χ),G]if either it is already removed after ρ,or it cannot be preserved by the specification(ψ,a,χ).Rule(✘2)corresponds to the semantics thatPlease note that it is always true that any a-arrow will be remove after ρ[(ψ,b,χ),G]if b≠ a.Therefore,we do not need a rule forσan,ρ[(ψ,b,χ),G],✘if b≠a.

The following proposition is obvious according to the tableau rules.

Proposition 18.Given a tableau T and a branch b ∈T,ifσ,ρ,x∈b and x=√/✘then σ=σ′an for some label σ′,a ∈A and n ∈N.

Definition 19(Closed tableau).A branch b is closed if and only if we have either{σ,ρ,p,σ,ρ′,¬p}⊆b for some σ,ρ,ρ′and p,or{σan,ϵ,√,σan,ϵ,✘}⊆b for some σan,otherwise it is open.A tableau is closed if and only if all its branches are closed,otherwise it is open.

Table 1:Tableau rules

Figure 5:Closed tableau for the formula[(q,a′,q),a′]□ap ∧¬□ap

Example 20.In Figure 5,the tableau method is used to show the validity of one instance of the formula of Proposition 6.The rightmost column shows which tableau rule is applied in each line.

Next,we will show the soundness,but first we need another definition.

Definition 21(Interpretation).Given a Kripke model M and a branch b,let f be a function from the labels used in b to WM.We say that f is an interpretation of b in M if the following hold.

· M,f(σ)⊨ρφ for eachσ,ρ,φ∈b;

Proposition 22.Let f be an interpretation of b in M.If b contains the premise of a rule in Table 1,then f can be extended to be an interpretation of b′for some b′∈B where B is the set of branches generated by applying the rule on b.

ProofIf the rule is(¬¬),(¬∧)or(∧),it is straightforward.We restrict our attention to the other rules.

1.Rule (¬□a):The premise of the rule (¬□a)isσ,ρ,¬□aφ.Since f in an interpretation of b in M andσ,ρ,¬□aφ∈b,we have that M,f(σ)⊨ρ¬□aφ.Let b′=b ∪{σan,ρ|a,√,σan,ρ|a,¬φ}where n is new in b,then we know that B= {b′}.Since M,f(σ)⊨ρ¬□aφ,it follows that there exists t ∈WMsuch that (f(σ),t) ∈*ρ|aand M,t ⊨ρ|a¬φ.Now let the function f′be f ∪{σant}.We then have(f′(σ),f′(σan)) ∈*ρ|aand M,f′(σan)⊨ρ|a¬φ.Therefore,f′is an interpretation of b′in M.

2.Rule(□a):Please note that B={b∪{σan,ρ|a,φ},b∪{σan,ρ|a,✘}}.For each label σan which is used in b,we have either(f(σ),f(σan))∈*ρ|aor(f(σ),f(σan))*ρ|a.It follows byσ,ρ,□aφ∈b that M,f(σ)⊨ρ□aφ.If(f(σ),f(σan)) ∈*ρ|athen we have M,f(σan)⊨ρ|aφ.Thus,f is an interpretation of the branch b ∪{σan,ρ|a,φ}.If(f(σ),f(σan))∉*ρ|a,f is an interpretation of the branch b ∪{σan,ρ|a,✘}.

3.Rule(¬[U,G]):We have that B={b ∪{σ,ρ,[U,G]¬φ}}.Since f is an interpretation andσ,ρ,¬[U,G]φ∈b,these follow that M,f(σ)⊨ρ¬[U,G]φ.By semantics,we have that M,f(σ)⊨ρ[U,G]¬φ.Therefore,f is an interpretation of b ∪{σ,ρ[U,G],¬φ}.

4.Rule([U,G]):We have that B={b ∪{σ,ρ[U,G],φ}}.Sinceσ,ρ,[U,G]φ∈b,this follows that M,f(σ)⊨ρ[U,G]φ.By semantics,we have M,f(σ)⊨ρ[U,G]φ.Therefore,f is an interpretation of b ∪{σ,ρ[U,G],φ}.

5.Rule (√1):Since the premise of this ruleσan,ρ[U,G],√is in b,this follows that (f(σ),f(σan)) ∈*ρ[U,G].By the semantics,we have that(f(σ),f(σan)) ∈* ρ and that there exists (ψ,a,χ) ∈ U such that M,f(σ)⊨ρψ and M,f(σan)⊨ρχ.Therefore, f is an interpretation of b ∪{σan,ρ,√,σ,ρ,ψ,σan,ρ,χ},and it is in B.

6.Rule (√2):Since f is an interpretation of b,the rule whose premise is in b cannot be (√2).If so,we should have (f(σ),f(σan)) ∈* (ρ[U,G]).However,since there are no a-arrow specifications in U,by semantics,we have that(f(σ),f(σan))*(ρ[U,G]).

7.Rule(✘1):Sinceσan,ρ[(ψ,a,χ),G],✘∈b,this follows that(f(σ),f(σan))* ρ[(ψ,a,χ),G].By semantics,we have either (f(σ),f(σan))∉*ρ or M,f(σ)⊭ρψ or M,f(σan)⊭ρχ.Therefore,f is an interpretation of at least one branch in B= {b ∪{σan,ρ,✘},b ∪{σ,ρ,¬ψ},b ∪{σan,ρ,¬χ}}.

8.Rule (✘2):Sinceσan,ρ[U,G],✘∈b,this follows that (f(σ),f(σan))∉*ρ[U,G].By semantics,we know thatρ[(ψ,a,χ),G].Therefore,we have (f(σ),f(σan))*ρ[(ψ,a,χ),G]for each (ψ,a,χ) ∈U.For the specification (ψ,a′,χ) ∈U and a′≠ a,it follows by semantics that*(ρ[(ψ,a′,χ),G])= Ø.Therefore,we have(f(σ),f(σan))*ρ[(ψ,a′,χ),G]for each(ψ,a′,χ)∈U.Thus f is an interpretation of b ∪{σan,ρ[(ψ,a′,χ),G],✘|(ψ,a′,χ)∈U}. □

Theorem 23(Soundness).If there is a closed tableau for¬φ0,then φ0is valid.

ProofLet T be the closed tableau for ¬φ0.Assuming that φ0is not valid,this follows that¬φ0is satisfiable.Let M,s ⊨¬φ0.Please note that the branch in the initial tableau for ¬φ0is the branch b= {0,ϵ,¬φ0}.Define the function f as f(0)=s.This follows that M,f(0)⊨¬φ0.Therefore,f is an interpretation of b in M.Please note that each branch in T is generated by extended b by applying rules in Table 1.By Proposition 22,this follows that there is some branch b′∈T such that f can be extended to be an interpretation of b′.This is contradictory with the fact that b′is closed.Therefore,φ0is valid. □

In the rest of the section,we prove completeness.First,we need another auxiliary definition.

Definition 24(Saturated tableau).A branch b is saturatediffit is saturated under all tableau rules,as defined below:

1. b is saturated under Rule(¬¬)iffσ,ρ,¬¬φ∈b impliesσ,ρ,φ∈b;

2. b is saturated under Rule(¬∧)iffσ,ρ,¬(φ ∧ψ)∈b impliesσ,ρ,¬φ∈b orσ,ρ,¬ψ∈b;

3. b is saturated under Rule(∧)iffσ,ρ,(φ ∧ψ)∈b impliesσ,ρ,φ∈b andσ,ρ,ψ∈b;

4. b is saturated under Rule(¬□a)iffσ,ρ,¬□aφ∈b implies that{σan,ρ|a,√,σan,ρ|a,¬φ}⊆b for some n ∈N;

5. b is saturated under Rule (□a)iffσ,ρ,□aφ∈b implies that for each σan occurring in b we haveσan,ρ|a,✘∈b orσan,ρ|a,φ∈b;

6. b is saturated under Rule(¬[U,G])iffσ,ρ,¬[U,G]φ∈b impliesσ,ρ[U,G],¬φ∈b;

7. b is saturated under Rule([U,G])iffσ,ρ,[U,G]φ∈b impliesσ,ρ[U,G],φ∈b;

8. b is saturated under Rule(√1)iffσan,ρ[U,G],√∈b implies{σan,ρ,√,σ,ρ,ψ,σan,ρ,χ}⊆b for some(ψ,a,χ)∈U;

9. b is saturated under Rule(√2)iffσan,ρ[U,G],√∈b implies{σan,ϵ,√,σ,ϵ,✘,}⊆b;

10. b is saturated under Rule(✘1)iffσan,ρ[(ψ,a,χ),G],✘∈b impliesσan,ρ,✘∈b orσ,ρ,¬ψ∈b orσan,ρ,¬χ∈b.

11. b is saturated under Rule(✘2)iffσan,ρ[U,G],✘∈b implies that{σan,ρ[(ψ,a′,χ),G],✘|(ψ,a′,χ)∈U}⊆b,where there are at least two specifications in U.

We say a tableau is saturatediffall its branches are saturated.

The following two propositions are obvious by the tableau rules.

Proposition 25.Given a saturated tableau T and a branch b ∈T,ifσan,ρ,√∈b thenσan,ϵ,√∈b.

Proposition 26.Given a saturated tableau T and a branch b ∈T,if a label σan occurs in b thenσan,ϵ,√∈b.

Definition 27(Length of term).The length of a formula is defined as follows:

The length of an update sequence is defined as follows:

The length of a term is defined as follows:

Please note that the length of the term(ϵ,φ)is the same as the length of φ.

Now,we are ready to prove the completeness.

Theorem 28(completeness).If φ0is valid,there is a closed tableau for¬φ0.

ProofWe only need to show that if all tableaux for φ0are open then φ0is satisfiable.Since each tableau for φ0can be extended to be saturated and there is at least one tableau for φ0,i.e.,the initial tableau,there exists an open and saturated tableau for φ0if all its tableaux are open.

Let T be an open and saturated tableau for φ0and b be an open and saturated branch of T.In order to show φ0is satisfiable,we only need to show that there is an interpretation of b(recall Definition 21).Next we will construct a model Mcand we will show that there is an interpretation of b in Mc.The model Mc=W,R,Vis defined as follows.

Please note that if σan is used in b then so is σ.

Let I be the function I(σ)= σ.By induction on the length of terms,we will show that I is an interpretation of b in Mc.For abbreviation,we will write I(σ)as σ.For the case of l(ρ,x)=0,the term(ρ,x)can only be of the form(ϵ,✘)or(ϵ,√).Furthermore,it cannot be of the form(ϵ,✘).Assuming(σan,ϵ,✘)∈b for some label σan,it follows by Proposition 26 that(σan,ϵ,√) ∈b,this is in contradiction with that b is open.Therefore,in this case,we only need to show that(σ,σan) ∈Rafor each σan with(σan,ϵ,√)∈b,which is obvious by the definition of the model Mc.

With the inductive hypothesis that each labelled term(σ,ρ,x)∈b with l(ρ,x)＜n satisfies the conditions declared in Definition 21,we will show that each labelled term(σ,ρ,x)∈b with l(ρ,x)=n also satisfies the conditions,where n ≥1.

If x is a formula,there are different cases according to the form of the formula,as below:

1.(σ,ρ,p)∈b:It is obvious that Mc,σ ⊨ρp.

2.(σ,ρ,¬p) ∈b:Assuming σ ∈V(p),it follows that(σ,ρ′,p) ∈b for some ρ′.This is in contradiction with the assumption that b is open.Therefore,we have σV(p),namely Mc,σ ⊨ρ¬p.

3.(σ,ρ,¬¬φ) ∈b:Since b is saturated,it follows that (σ,ρ,φ) ∈b.Since l(ρ,φ) ＜l(ρ,¬¬φ),it follows by IH that Mc,σ ⊨ρφ.Therefore,we have Mc,σ ⊨ρ¬¬φ.

4.(σ,ρ,φ ∧ψ) ∈ b:Since b is saturated,it follows that (σ,ρ,φ) ∈ b and(σ,ρ,ψ) ∈ b.Since l(ρ,φ),l(ρ,ψ) ＜ l(ρ,φ ∧ψ),it follows by IH that Mc,σ ⊨ρφ and Mc,σ ⊨ρψ.Therefore,we have Mc,σ ⊨ρφ ∧ψ.

5.(σ,ρ,¬(φ ∧ψ)) ∈b:Since b is saturated,it follows that (σ,ρ,¬φ) ∈b or(σ,ρ,¬ψ) ∈b.Since l(ρ,¬φ),l(ρ,¬ψ) ＜l(ρ,¬(φ ∧ψ)),it follows by IH that Mc,σ ⊨ρ¬φ or Mc,σ ⊨ρ¬ψ.Therefore,we have Mc,σ ⊨ρ¬(φ ∧ψ).

7.(σ,ρ,□aφ) ∈b:Let σ′∈W be a state with(σ,σ′) ∈Ra*(ρ|a).In order to show Mc,σ ⊨ρ□aφ,we need to show that Mc,σ′⊨ρ|aφ.Since Ra*(ρ|a)⊆Ra,it follows that σ′= σan for some n ∈N.Assuming (σan,ρ|a,✘) ∈b,it follows by IH that(σ,σan)∉Ra*(ρ|a).This is in contradiction with the assumption that (σ,σ′) ∈Ra*(ρ|a).Therefore,we have (σan,ρ|a,✘)∉b.Since b is saturated,it follows that (σan,ρ|a,φ) ∈b.It follows by IH that Mc,σan ⊨ρ|aφ.

8.(σ,ρ,¬[U,G]φ) ∈b:Since b is saturated,it follows that(σ,ρ[U,G],¬φ) ∈b.Since l(ρ[U,G],¬φ)＜l(ρ,¬[U,G]φ),it follows by IH that Mc,σ ⊨ρ[U,G]¬φ.Therefore,we have Mc,σ ⊨ρ¬[U,G]φ.

9.(σ,ρ,[U,G]φ) ∈b:Since b is saturated,it follows that (σ,ρ[U,G],φ) ∈b.Since l(ρ[U,G],φ) ＜l(ρ,[U,G]φ),it follows by IH that Mc,σ ⊨ρ[U,G]φ.Therefore,we have Mc,σ ⊨ρ[U,G]φ.

If x in the term(ρ,x)is of the form√or✘,we have ρ is not ϵ because l(ρ,x)≥1.There are different cases,as below:

1.(σan,ρ[U,G],√) ∈b and there exists an a-arrow specification in U:Since b is saturated,it follows that{σan,ρ,√,σ,ρ,ψ,σan,ρ,χ} ⊂b for some(ψ,a,χ) ∈U.Since l(ρ,√),l(ρ,ψ),l(ρ,χ) ＜l(ρ[U,G],√),it follows by IH that(σ,σan) ∈Ra*ρ, Mc,σ ⊨ρψ and Mc,σan ⊨ρχ.It follows that(σ,σan)∈Ra*(ρ[U,G]).

2.(σan,ρ[U,G],√) ∈b and there are no a-arrow specifications in U:Due to Rule(√2)and the fact that b is open and saturated,this case is impossible.

3.(σan,ρ[(ψ,a′,χ),G],✘)∈b:If a′≠a,it follows that Ra*(ρ[(ψ,a′,χ),G])=Ø.It is obvious (σ,σan)Ra* (ρ[(ψ,a′,χ),G]).If a′= a,it follows by Rule (✘1)thatσan,ρ,✘∈b,orσ,ρ,¬ψ∈b,orσan,ρ,¬χ∈b.Since l(ρ,✘),l(ρ,¬ψ),l(ρ,¬χ) ＜l(ρ[(ψ,a,χ),G],✘),it follows by IH that(σ,σan)Ra*ρ,or Mc,σ ⊨ρ¬ψ,or Mc,σan ⊨ρ¬χ.Each of them can derive that(σ,σan)Ra*(ρ[(ψ,a,χ),G]).

4.(σan,ρ[U,G],✘) ∈b and |U| ≥2:If there are no a-arrow specifications in U,it is obvious that (σ,σan)Ra* (ρ[U,G])since Ra* (ρ[U,G])= Ø.Otherwise,let(ψ1,a,χ1),···,(ψk,a,χk)be all the a-arrow specifications in U.Since b is saturated,it follows by Rule(✘2)thatσan,ρ[(ψi,a,χi),G],✘∈b for all 1 ≤i ≤k.Since l(ρ[(ψi,a,χi),G],✘)＜l([U,G],✘)for all 1 ≤i ≤k due to|U|≥2,it follows by IH that(σ,σan)Ra*(ρ[(ψi,a,χi),G])for all 1 ≤i ≤k.Since Ra*(ρ[U,G])=∪1≤i≤kRa*(ρ[(ψi,a,χi),G]),we have(σ,σan)Ra*(ρ[U,G]).

We have shown that all labelled terms in b satisfy the conditions declared in Definition 21.Since0,ϵ,φ0∈b,thus we have Mc,0 ⊨φ0. □

4 Decidability

In this section,we will show that PAUL is decidable,that is,the problem whether an PAUL formula φ is satisfiable can be answered in a finite number of steps.Please note that Theorem 9 already tells us that each formula φ in PAUL can be equivalently reduced to be a formula with out updates,i.e.,a formula in normal modal logic K.We can see that PAUL is the same with K if it is confined on formulas with out updates.Since K is decidable,this follows that PAUL is decidable.However,as it is shown in[15],the equivalent translation from PAL to K might be exponential.Since PAL can be polynomially translated into PAUL by replacing the PAL operator [φ]with[U,Agt]where U= {(φ,a,φ) | a ∈Agtoccurs in φ},the equivalent translation from PAUL to K might be exponential too.In this section,we will directly prove the decidability of PAUL,based on the tableau system presented in the previous section.

Our method is to show that PAUL has small model property.We will show that each satisfiable PAUL formula φ has a bounded small model in which φ is true.From the proof of Theorem 28,we have seen that we can construct a model for φ based on a saturated open branch if φ is satisfiable,and each state in the model is exactly a label used in the branch.Therefore,the key is to show that there are only finitely many labels used in the tableau branch.

For the commonly used tableau calculus for normal modal logic,each formula occurring in the tableau is a subformula of the destination formula,and this feature plays an important role to show the decidability of normal modal logic through tableau method.Similarly,we will define the notation of subterm here,and we will show that all terms occurring in the tableau are subterms.

Definition 29(Subterm).Given a term(ρ,x),the set of subterm of(ρ,x),denoted as sub(ρ,x),is defined as below.

Let sub+(ρ,x)be the set{(ρ,¬φ)|(ρ,φ)∈sub(ρ,x)}∪sub(ρ,x).

The following proposition states some properties of the subterm set.

Proposition 30.We have the following results.

· sub(ρ,x)is finite;

· (ρ,✘/√)∈sub(ρ,φ);

· (ρ,x)∈sub(ρ′,x′)implies sub(ρ,x)⊆sub(ρ′,x′).

Proposition 31.Let T be a tableau for φ0and b be a branch of T.If(σ,ρ,x) ∈b

then(ρ,x)∈sub+(ϵ,φ0).

ProofAccording to Definition 17,we prove this by induction on the process of construction of T.For the initial tableau{{(0,ϵ,φ0)}},it is obvious.Next,we only need to show that all the tableau rules in Table 1 preserve the subterm property.The cases of the rules(¬¬),(¬∧),(∧),([U,G])and(✘2)are obvious;we will restrict our attention to the other rules.

1.Rule(¬□a):If(ρ,¬□aφ)∈sub+(ϵ,φ0),then we have(ρ,□aφ)∈sub(ϵ,φ0).Because (ρ|a,φ) ∈sub(ρ,□aφ),it follows by Proposition 30 that (ρ|a,√),(ρ|a,φ)∈sub+(ϵ,φ0).

2.Rule (□a):If (ρ,□aφ) ∈sub+(ϵ,φ0),then we have (ρ,□aφ) ∈sub(ϵ,φ0).Because (ρ|a,φ) ∈sub(ρ,□aφ),it follows by Proposition 30 that (ρ|a,✘),(ρ|a,φ)∈sub+(ϵ,φ0).

3.Rule(¬[U,G]):If(ρ,¬[U,G]φ) ∈sub+(ϵ,φ0),then we have(ρ,[U,G]φ) ∈sub(ϵ,φ0).Since(ρ[U,G],φ)∈sub(ρ,[U,G]φ),it follows by Proposition 30 that(ρ[U,G],φ)∈sub(ρ,φ0).Therefore,we have(ρ[U,G],¬φ)∈sub+(ρ,φ0).

4.Rule (√1):If (ρ[U,G],√) ∈sub+(ϵ,φ0)then (ρ[U,G],√) ∈sub(ϵ,φ0).Let (ψ,a,χ) ∈U.We have (ρ[(ψ,a,χ),G],√) ∈sub(ϵ,φ0).Since (ρ,ψ),(ρ,χ) ∈sub(ρ[(ψ,a,χ),G],√),we have(ρ,ψ),(ρ,χ) ∈sub(ϵ,φ0).It follows by Proposition 30 that (ρ,√) ∈sub(ρ,ψ),thus we also have (ρ,√) ∈sub(ρ,φ0).

5.Rule(√2):It follows by Proposition 30 that(ϵ,√),(ϵ,✘)∈sub(ϵ,φ0).

6.Rule (✘1):If (ρ[(ψ,a,χ),G],✘) ∈sub+(ϵ,φ0),then (ρ[(ψ,a,χ),G],✘) ∈sub(ϵ,φ0).Since (ρ,ψ),(ρ,χ) ∈sub(ρ[(ψ,a,χ),G],✘),we have (ρ,ψ),(ρ,χ) ∈sub(ϵ,φ0).Therefore,we have (ρ,¬ψ),(ρ,¬χ) ∈sub+(ϵ,φ0).It follows by Proposition 30 that(ρ,✘) ∈sub(ρ,ψ),thus we also have(ρ,✘) ∈sub(ρ,φ0). □

Proposition 32.Let T be a tableau for φ0,and let b be a branch of T.If σ is a label present in b,then there are at most k labels present in b with the form of σan for some n ∈N,where k=|sub+(ϵ,φ0)|.

ProofIt follows by Definition 17 that each label σan present in b is generated by applying the rule(¬□a)to a labelled term(σ,ρ,¬□aφ) ∈b.According to Proposition 31,there are at most k terms labelled with σ in b.Therefore,there are at most k labels present in b with the form of σan for some n ∈N. □

Definition 33(Length of label).The length of a label σ,denoted by|σ|,is defined by induction on σ: |n|=0;|σan|=|σ|+1.

Proposition 34.Let T be a tableau for φ0and b be a branch of T.If(σ,ρ,x) ∈b then|σ|≤l(φ0)-l(ρ,x).

ProofFollowing Definition 17,the proof is by induction on the process of construction of T.For the initial tableau{{(0,ϵ,φ0)}},it is obvious.Next we will show that this property is preserved by all the tableau rules.The cases of the rules(¬¬),(¬∧),(∧)and(√2)are obvious;we will restrict our attention to the other rules.

3.Rule(¬[U,G]):If|σ|≤l(φ0)-l(ρ,¬[U,G]φ),we have l(φ0)-l(ρ,¬[U,G]φ)≤l(φ0)-l(ρ[U,G],¬φ)because l(ρ,¬[U,G]φ)=l(ρ[U,G],¬φ)+1.Therefore,we have|σ|≤l(φ0)-l(ρ[U,G],¬φ).

4.Rule ([U,G]):Since l(ρ,[U,G]φ)= l(ρ[U,G],φ)+1,if |σ| ≤l(φ0) -l(ρ,[U,G]φ),we have|σ|≤l(φ0)-l(ρ[U,G],φ).

5.Rule (√1):Assume |σan| ≤l(φ0) -l(ρ[U,G],√).Since l(ρ[U,G],√) ≥l(ρ,√),it follows that|σan| ≤l(φ0)-l(ρ,√).Let(ψ,a,χ) ∈U.We have l(ρ[U,G],√) ≥l(ρ,ψ)-1 because l(ρ[U,G],√) ≥l(ρ,ψ).It follows that l(φ0)-l(ρ[U,G],√) ≤l(φ0)-l(ρ,ψ)+1.Thus we have|σan| ≤l(φ0)-l(ρ,ψ)+1.It follows that|σ|≤l(φ0)-l(ρ,ψ).What is more,since l(ρ[U,G],√)≥l(ρ,χ),it follows that l(φ0)-l(ρ[U,G],√)≤l(φ0)-l(ρ,χ).Thus we have|σan|≤l(φ0)-l(ρ,χ).

6.Rule(✘1):Assume that|σan| ≤l(φ0)-l(ρ[(ψ,a,χ),G],✘).Since we have l(ρ[(ψ,a,χ),G],✘)≥l(ρ,✘),it follows that|σan|≤l(φ0)-l(ρ,✘).What is more,since l(ρ[(ψ,a,χ),G],✘)≥l(ρ,¬ψ)and l(ρ[(ψ,a,χ),G],✘)≥l(ρ,¬χ),it follows that l(φ0)-l(ρ[(ψ,a,χ),G],✘) ≤l(φ0)-l(ρ,¬ψ)and l(φ0)-l(ρ[(ψ,a,χ),G],✘)≤l(φ0)-l(ρ,¬χ).Therefore,we have|σan|≤l(φ0)-l(ρ,¬ψ)and|σan|≤l(φ0)-l(ρ,¬ψ).Since|σ|≤|σan|,it is obvious|σ|≤l(φ0)-l(ρ,¬ψ).

7.Rule(✘2):Assume|σan| ≤l(φ0)-l(ρ[U,G],✘)and|U| ≥2.Suppose that(ψ,a′,χ) ∈U,we have l(ρ[U,G],✘) ≥l(ρ[(ψ,a′,χ),G],✘).It follows that l(φ0)-l(ρ[U,G],✘) ≤l(φ0)-l(ρ[(ψ,a′,χ),G],✘).Thus we have|σan| ≤l(φ0)-l(ρ[(ψ,a′,χ),G],✘). □

Lemma 1(Small model property).If φ0is satisfiable then φ0is satisfiable in a model which is bounded by kO(m),where k=|sub+(ϵ,φ0)|and m=l(φ0).

ProofIt follows by Theorem 23 that all tableaux for φ0are open.According to the proof of Theorem 28,we can construct a model Mcfrom a saturated branch b such that φ0is satisfied in Mc.By the definition of Mc,we know that each state in Mcis a label present in b.Please note that all labels present in b form a tree.It follows by Proposition 32 that each label in the tree has at most k children.It follows by Proposition 34 that the depth of the tree is bounded by m.Therefore,there are at most kO(m)labels used in b. □

Theorem 35(Decidability).The problem whether φ0is satisfiable is decidable.

ProofIt follows by Lemma 1 that we only need to check all the models no bigger than kO(m)where k=|sub+(ϵ,φ0)|and m=l(φ0),and this procedure can terminate in finitely many steps. □

5 Conclusion

This paper presented the framework of Private Arrow Update Logic (PAUL),which extends the arrow update of AUL with a relativized subgroup of agents.Public,private and semi-private announcements can be modeled in this framework.PAUL still is a particular case of GAUL,since some information change,like cheating,cannot be modeled in PAUL.This paper also provided a sound and complete tableau method of PAUL and showed that PAUL is decidable.

For future research,we can try to give an optimal algorithm for the satisfiability problem of PAUL by taking a depth-first search strategy on the tableau method.Since the normal modal logic K is a fragment of PAUL and K is PSPACE-complete,PAUL is at least PSPACE-hard.With an optimal search algorithm on the tableau,we conjecture that there might be a PSPACE upper bound for PAUL.What is more,since each AUL formula can be equivalently translated into a PAUL formula by replacing the update[U]by[U,Agt],the tableau method presented in this paper can apply to AUL.Therefore,the optimal algorithm for PAUL(if there is one)will also be an algorithm for AUL and might also be optimal.

One direction for future study is to see how frame conditions are handled in arrow update logic.For example,if the original model is based on a symmetric frame,we might ask the symmetry is preserved after update.This could be done by asking the update U to satisfy some conditions.If the update U satisfies that(φ,a,ψ) ∈U implies(ψ,a,φ)∈U,then symmetry would be preserved.If(φ,a,ψ),(ψ,a,χ)∈U implies(φ,a,χ)∈U,then transitivity would be preserved.The difficulty lies in how to preserve reflexivity.We doubt it might not be solved if we only confine the form of the update U.

Another direction for future research is to use PAUL to model the information change in logics of knowing how (cf.[19,9]).The main feature of Arrow Update Logic is that it updates information but does not eliminate states.This makes it more suitable for modeling information update in knowing how.For example,a doctor may not know how to treat a patient since the only two available medicines a1and a2may cause some very bad side-effect.That is,there is an a1-arrow and an a2-arrow from the current state to the bad side-effect state.If the information is updated,for example,a new scientific discovery shows that a1will not cause the bad effect,then the doctor should know how to treat the patient.This kind of information update will eliminate arrows but not states.

逻辑学研究

2020年6期