Comparing Fixed-Point and Revision Theories of Truth from the Perspective of Paradoxicality*
2020-12-24QiqingLin
Qiqing Lin
Abstract. For the aim“to get a sense of the lay of the land amid a variety of options”,Kremer(2009)defined three relations to compare ten fixed-point theories suggested by Kripke(1975)and three revision theories considered by Gupta and Belnap (1993).This paper extends Kremer’s comparative work by comparing these theories from another important perspective,the perspective of paradoxicality.The notion of paradoxicality is very important for theories of truth,which has influenced philosophers’choice of specific theory of truth.We define a new relation in terms of this perspective,and establish the relationship among the thirteen theories of truth according to this relation.
1 Introduction
In 1975,Kripke put forward the fixed-point theory of truth in [7].Martin and Woodruff independently proposed this theory at almost the same time in [9].With the publication of Kripke ([7])and Martin and Woodruff ([9]),“not only was it established once and for all that three-valued languages could contain T-predicates for themselves,but tools became available that could be used to construct systematic theories of truth.”([3],p.58)
The basic idea of the fixed-point theory of truth is that paradoxical sentences such as the Liar sentence are neither true nor false.Interpreting the truth predicate as a fixed point can guarantee that the truth value of any sentence A is the same as the one of the sentence that“A”is true.In[7],Kripke provided an inductive construction according to which we can construct fixed points of the jump operators derived from certain kind of three-valued valuation schemes,and he pointed out that those jump operators not only have a least fixed point,but also have a greatest intrinsic fixed point.The inductive construction for constructing fixed points applies to the strong Kleene scheme κ,the weak Kleene scheme μ,the van Fraassen’s supervaluation scheme,σ,and some variants of σ(including σ1and σ2).
Kripke([7])did not make any particular recommendation among the three-valued valuation schemes to which the inductive construction applies.Neither did he make any firm recommendation among the fixed points of a given valuation scheme.Kripke did think the least fixed point as “the most natural” interpretation for the intuitive concept of truth,and the greatest intrinsic fixed point as“the unique‘largest’interpretation”consistent with our intuitive idea of truth.
In the fixed-point theory of truth,a sentence is defined to be paradoxical if it has no truth value in any fixed point.
The revision theory of truth is a competitive theory of the fixed-point theory of truth.In 1982,Herzberger suggested this theory in[4],and Gupta independently put forward this theory in[2].They came up with the theory for different reasons.Since the inductive construction for constructing fixed points provided by Kripke does not apply to the classical valuation scheme, τ,and “it is reasoning in accordance with classical logic which in the first instance gives rise to the semantic paradoxes”([4],p.61),Herzberger adapted Kripke’s inductive construction for admitting the classical valuation scheme.The revision theory of truth was thus suggested by Herzberger.Gupta proposed this theory to solve the descriptive problem about the truth concept1Gupta has distinguished two different problems that the Liar paradox raises about the concept of truth in his paper[2],the descriptive one and the normative one.The descriptive problem is described as follows:“The first is the descriptive problem of explaining our use of the word‘true’,and,in particular,of giving the meaning of sentences containing ‘true’.” ([2],p.1)The normative one is described as follows:“The second problem that the liar paradox raises about the concept of truth is the normative one of discovering the changes(if any)that the paradox dictates in our conception and use of‘true’.”([2],p.1–2),basing on the following idea:“When we learn the meaning of‘true’what we learn is a rule that enables us to improve on a proposed candidate for the extension of truth.”([2],p.37)This rule is called“the revision rule for truth”in[2].
In the revision theory of truth,sentences are classified according to their behavior in revision sequences,which are ordinal-length sequences based on the revision rule.A limit rule is needed to determine the objects of a revision sequence at limit stages.Hence,different limit rule policies adopted lead to different resultant revision theories.The limit rule policy adopted by Herzberger([4])is different from the one adopted by Gupta([2]).Belnap criticized Gupta’s limit rule policy,and suggested another limit rule policy(and hence another resultant revision theory)in[1].
In Gupta and Belnap’s monograph([3]),they provided a clear philosophical basis for the following idea:“the signification of truth is a rule of revision.”([3],p.139)2Gupta and Belnap defined the notion of signification as follows:“Let the(extensional)signification of an expression (or a concept)in a word w be an abstract something that carries all the information about the expression’s extensional relations in w.”([3],p.30)They concluded that“Signification is a generalization of the notion of extension.”([3],p.30)They viewed Tarski biconditionals as Tarski suggested,i.e.,as partial definitions of the truth concept.Hence,they reckoned the truth concept is a circular concept and its signification is a revision rule determined by its definition,i.e.,the totality of all Tarski biconditionals.Three revision theories have been presented in detail by Gupta and Belnap([3]),denoted byT*,T#andTCrespectively.T*is actually the theory proposed by Belnap in[1].
In the revision theory of truth,a sentence is defined to be paradoxical if,it is unstable or not nearly stable in all or certain kind of revision sequences.
Kremer introduced three binary relations,≤1,≤2and ≤3,to compare fixed-point and revision theories of truth,for the point“to get a sense of the lay of the land amid a variety of options”.([5],p.363)According to the three relations,he established the relationships among ten fixed-point theories suggested by Kripke in [7],and three revision theories considered by Gupta and Belnap in[3].The ten fixed-point theories are respectively based on the least fixed point or the greatest intrinsic fixed point of one of the five three-valued valuation schemes,κ,μ,σ,σ1and σ2.The three revision theories compared by Kremer([5])areT*,T#andTC.
≤1,≤2and ≤3represent three different perspectives to compare theories of truth.For example,≤1is defined according to the perspective of validity.3Readers can consult[5,p.372–377]for detailed motivations of ≤1,≤2,and ≤3.
In[6],Kremer used the comparative results in[5]to critique on a claim of Gupta and Belnap in[3]:“An important feature of the revision theory,and one that prompted our interest in it,is its consequence that truth behaves like an ordinary classical concept under certain conditions—conditions that can roughly be characterized as those in which there is non-vicious reference in the language.”([3],p.201)After considering notions of “truth behaving like an ordinary classical concept” and notions of“non-vicious reference”generated both by revision theories and by fixed-point theories,Kremer showed that some fixed-point theories have an advantage analogous to what Gupta and Belnap claimed for their approach,andT#does not have the advantage.
Kremer’s comparative work is very meaningful,which helps us to know more about the thirteen theories of truth and the relationships among them.His work is also very useful:for example,it helps us to get a better understanding of Gupta and Belnap’s claim introduced above.
In addition to the three natural perspectives in Kremer’s comparative work,it is also meaningful to compare theories of truth from the perspective of paradoxicality.The notion of paradoxical is an important notion for theories of truth.On the one hand,it is often the case that in formal theories of truth,the definition of paradoxicality is provided as soon as the signification of the truth concept is presented.On the other hand,this notion influences philosophers’choice of concrete theories of truth.When Gupta proposed the revision theory of truth in[2],one of the two reasons for which Gupta adopted a limit rule policy different from the one adopted by Herzberger([4]),is that he reckoned the revision theory resulting from the limit rule policy adopted by Herzberger misclassifies certain sentences,which should be paradoxical according to Gupta’s intuition ([2],p.53).In [10],Yaqūb provided four kinds of artifacts to criticizeT*,T#andTC(and raised his own revision theory),two of which are related to the assertion of paradoxical sentences.
In a word,it is significant to compare theories of truth from the perspective of paradoxicality.This paper define a new relation according to the perspective of paradoxicality,denoted by ≤4,among the thirteen theories of truth considered in Kremer’s comparative work([5]),and establish the relationship among the theories according to this relation.
The rest of this paper is structured as follows.The next section introduces the ten fixed-point theories of truth.The third section introducesT*,T#andTC.In the fourth section,the thirteen theories of truth are compared according to the relation≤4.This paper is concluded in Section 5.
2 Fixed-point Theories of Truth
Denote the set of all sentences of a first-order language L by Sent(L).If L and L+are two first-order languages such that L+includes only all the symbols of L and an additional 1-place predicate symbolT,andAis a constant symbol of L for any A ∈Sent(L+),then say that L+is a truth language,and L is the ground language of L+.Ais called a quote name in L+.If M=D,Iis a classical model for L satisfying the condition that Sent(L+)⊆D and I(A)=A for each A ∈Sent(L+),then say that M is a ground model of L+.
Given a first-order language L,call M=D,Ia three-valued model for L if it satisfies the following conditions:(1)D is a nonempty set;and(2)I is a function the domain of which is the set of the nonlogical symbols of L such that it maps every constant symbol to an element of D,every n-place function symbol to a function from Dnto D,and every n-place predicate symbol to a function from Dnto the truth value set{t,f,n}.Given a model M and a valuation scheme ρ that applies to M,the truth value of sentence A in M according to ρ is denoted by
In κ and μ,negation is treated in the same way: ¬t=f,¬f=t,and¬n=n.In κ,conjunction is treated as follows: ∧(x,y)=t iff x=y=t,and ∧(x,y)=f iff x=fory=f.And κ treats universal quantifier analogously to conjunction.In μ,conjunction is treated as follows: ∧(x,y)=t iff x=y=t,and ∧(x,y)=n iff x=nory=n.And universal quantifier is treated analogously to conjunction in μ too.
Order the truth values as follows:n≤n≤t≤t,andn≤f≤f.Given two three-valued models for L,M=D,Iand M′=D,I′,and an n-place predicate symbol R,if for any d1,d2,...,dn∈D,I(R)(d1,d2,...,dn) ≤I′(R)(d1,d2,...,dn),then I(R) ≤I′(R). M ≤M′if I and I′agree on all constant symbols and function symbols,and I(R) ≤I′(R)for each predicate symbol R.Given a threevalued model M and a sentence A,(A)is defined as follows:

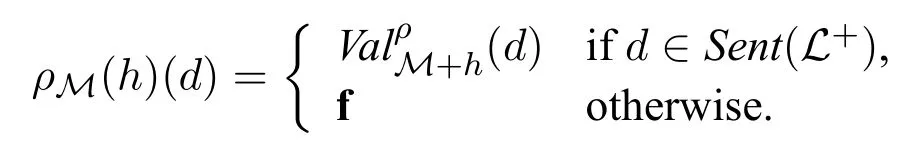
Given any truth language L+and any ground model M=D,Iof L+,Kripke([7])provided an inductive construction to construct fixed points of jump operators derived from certain kind of three-valued valuation schemes,in which the monotonicity of a jump operator plays a crucial role.
A jump operator ρMis monotone if,for all hypotheses h and h′in the domain of ρMsuch that h ≤h′, ρM(h) ≤ρM(h′).Taking κ as an example,Kripke ([7])constructed a fixed point according to the inductive construction.

When applied to κMand beginning with the empty hypothesis,Kripke’s inductive construction can be represented as follows:for every ordinal α,
if α=0,then let hα=h;
if α=β+1,then let hα=κM(hβ);and
if α is a limit ordinal,then let
Since κMis a total function on the set of all hypotheses and is monotone,it can be proved that a unique ordinal-length sequence of hypotheses is obtained in this way(denoted byhα| α ∈On,where On denotes the class of all ordinals),and that for all ordinals α ≤α′,hα≤hα′.Since the cardinality of the set of all hypotheses is bounded,there must be ordinals α <α′such that hα= hα′.So hα= hα+1=κM(hα),i.e.,hαis a fixed point of κM.
Kripke pointed out that the fixed point obtained above is the least fixed point of κMand that the same way can be used to construct the least fixed point of μMand that of σM.
Let ρ= κ, μ, σ.Kripke([7])showed that for any truth language L+and any ground model M=D,Iof L+,ρMhas a greatest intrinsic fixed point.Following[5],the least fixed point of ρMis denoted by lfp(ρM),and the greatest intrinsic fixed point of ρMis denoted by gifp(ρM).
For any truth language L+and any ground model M of L+,Kripke’s inductive construction for constructing fixed points applies to two variants of σMthat are denoted by σ1Mand σ2Mrespectively in [5].Given that Γ is a set of sentences,if there is no sentence A such that both A and ¬A are classical first-order consequences of Γ,then say that Γ is consistent.Given a hypothesis h,if the set{A ∈Sent(L+) | h(A)=t}is consistent,then say that h is weakly consistent;and if the set{A ∈Sent(L+)|h(A)=t}∪{¬A|A ∈Sent(L+),h(A)=f}is consistent,then say that h is strongly consistent. σ1Mis a function from weakly consistent hypotheses to weakly consistent hypotheses such that for every weakly consistent hypothesis h,every d ∈D,

σ2Mis a function from strongly consistent hypotheses to strongly consistent hypotheses such that for every strongly consistent hypothesis h,every d ∈D,

Both σ1Mand σ2Mare monotone,and have both a least least fixed point and a greatest intrinsic fixed point.Following [5], σ1and σ2are treated as two three-valued valuation schemes.
Let L+be a truth language,and M be a ground model of L+.Kremer([5])has considered ten fixed-point theories,Tlfp,ρandTgifp,ρfor each ρ ∈{κ,μ,σ,σ1,σ2}.The fixed-point theoryTlfp,ρdictates that the interpretation ofTin the ground model M is the least fixed point of ρM.The fixed-point theoryTgifp,ρdictates that the interpretation ofTin the ground model M is greatest intrinsic fixed point of ρM.
For any hypothesis (relative to M=D,I) h and any d ∈D,if h(d)=t(h(d)=f,h(d)=n),then say that h declares d true(false,neither true nor false).
Definition 1.Let L+be a truth language, M be a ground model of L+, ρ= κ, μ,σ,σ1or σ2,and A ∈Sent(L+).Say that A is paradoxical in the ground model M according to the theoryTlfp,ρ(or the theoryTgifp,ρ)if all fixed points of ρMdeclare A neither true nor false.
3 Revision Theories of Truth
Given a truth language L+and a ground model M=D,Iof L+,a revision rule for truth,τM,is a function from classical hypotheses to classical hypotheses such that for every classical hypothesis h,every d ∈D,
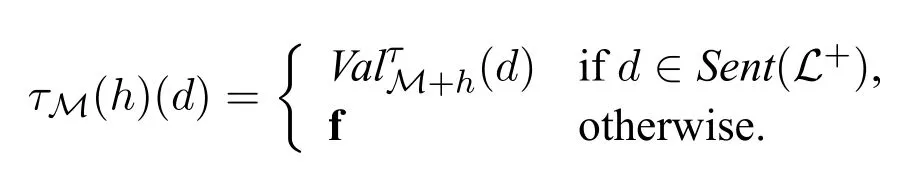
For any truth language L+and any ground model M of L+,the following propositons hold:(1) μM(h) ≤ κM(h) ≤ σM(h)for every hypothesis h; (2)σM(h)≤σ1M(h)for every weakly consistent hypothesis h;(3)σ1M(h)≤σ2M(h)for every strongly consistent hypothesis h;(4)τM(h)=μM(h)=κM(h)=σM(h)for every classical hypothesis h; (5)τM(h)= σ1M(h)for every weakly consistent classical hypothesis h;and(6)τM(h)= σ2M(h)for every strongly consistent classical hypothesis h.
For any sequence S,lh(S)is used to denote the length of S,and for any β <lh(S),Sβis used to denote the βth object of S.Given a ground model M=D,Iof a truth language L+,and a sequence of classical hypotheses S whose length is some limit ordinal or On.Suppose that α is a limit ordinal such that α ≤lh(S).If there is an ordinal β such that β <α,and for every β ≤δ <α, Sδ(d)=t(Sδ(d)=f),then say that d is stably true(stably false)up to α in S.If d is either stably true or stably false up to α,then say that d is stable up to α in S;otherwise,d is unstable up to α in S.
Given a revision sequence S and any element d in the domain,if there is an ordinal α such that for every α ≤β, Sβ(d)=t(Sβ(d)=f),then say that d is stably true (false)in S.If d is stably true or stably false in S,then say that d is stable in S;otherwise,d is unstable in S.
Given a revision sequence S and any element d in the domain,if there is an ordinal α such that for every α ≤β,there is a natural number n such that for every m ≥n,Sβ+m(d)=t(Sβ+m(d)=f),then say that d is nearly stably true (nearly stably false)in S.If d is either nearly stably true or nearly stably false in S,then say that d is nearly stable in S;otherwise,d is not nearly stable in S.
Given a ground model M of a truth language L+and a hypothesis h(relative to M),if the set{A ∈Sent(L+) | h(A)=t}is maximally consistent,then say that h is maximally consistent.Given any classical hypothesis h,h is strongly consistentiffh is maximally consistent.Given a revision sequence S,if for every ordinal α,Sαis maximally consistent,then say that S is a C-sequence.4Note that for any revision sequence S,every ordinal α,Sα+1 is maximally consistent.
T*is the revision theory that classifies sentences according to their stability in all revision sequences.T#is the revision theory that classifies sentences according to their near stability in all revision sequences.TCis the revision theory that classifies sentences according to their stability in all C-sequences.
Definition 2.Let L+be a truth language, M be a ground model of L+,and A ∈Sent(L+).Say that A is paradoxical in the ground model M according to the theoryT*if A is unstable in any revision sequence.Say that A is paradoxical in the ground model M according to the theoryT#if A is not nearly stable in any revision sequence.Say that A is paradoxical in the ground model M according to the theoryTCif A is unstable in any C-sequence.
4 Relationship among the Theories of Truth
In this section,the thirteen theories of truth are compared from the perspective of paradoxicality:
Definition 3.Given any two theoriesTandT′among the thirteen theories,say thatT≤4T′ifffor every truth language L+,every ground model M of L+,and every sentence A ∈Sent(L+),if A is paradoxical in M according toTthen A is paradoxical in M according toT′.Say thatT≡4T′iff T≤4T′andT′≤4T.Note that ≤4is reflexive and transitive.
Theorem 4.Figure 1 uses an arrow to represent that the relation ≤4holds between the theory at the start of the arrow and the one at the end of the arrow.When restricted to the ten fixed-point theories,the relation ≤4is the reflexive transitive closure of the relation shown in Figure 1.

Figure 1
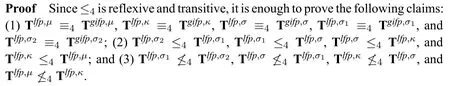
(1)holds by Definition 1.
The proof of (2)is as follows.Choose ρ and ρ′from the list μ, κ, σ, σ1, σ2such that ρ is to the left of ρ′.Next,we prove thatGiven any truth language L+and any ground model M of L+,and any fixed point h of ρM,note that h is strongly consistent,and h is sound relative tosince h=ρM(h)≤Hence a fixed point ofcan be constructed according to Kripke’s inductive construction,which is the least fixed point larger than or equal to h.In other words,for any fixed point h of ρM,there is a fixed point oflarger than or equal to h.Given any A ∈Sent(L+),suppose that A is paradoxical in M according to the theoryTlfp,ρ′,i.e.,all fixed points ofdeclare A neither true nor false.Hence all fixed points of ρMmust declare A neither true nor false. A is paradoxical in M according to the theory
The proof of(3)is as follows.Consider a truth language L+without any nonlogical symbols except forT,quote names,and a nonquote names a.Let M=D,Ibe the ground model of L+where I(a)=¬Ta.Note that for each ρ ∈{μ,κ,σ,σ1,σ2},and any fixed point h of ρM,h(¬Ta)=n,and h(Ta)=n.5¬T a can be regarded as a formalization of the Liar sentence.
(3.1)Consider the sentenceT¬Ta∨TTa.Let S be the unique ordinal-length sequence of hypotheses obtained in the construction of the least fixed point of σ2Maccording to Kripke’s inductive construction,where S0is the empty hypothesis.Note that S is an increasing sequence of hypotheses.For every strongly consistent classical hypothesis h ≥S0, h must declare only one of ¬Ta andTa true.Hence,σ2M(S0)must declareT¬Ta∨TTatrue.So lfp(σ2M)declaresT¬Ta∨TTatrue.ThereforeT¬Ta∨TTais not paradoxical in M according to the theoryTlfp,σ2.For any fixed point h of σ1M,it is not the case that h declaresT¬Ta∨TTafalse,since there is a fixed point of σ2Mlarger than or equal to h.And since h is strongly consistent,there is a weakly consistent classical h′such that h ≤h′and h′(¬Ta)=f,and h′(Ta)=f.Hence, τM(h′)declaresT¬Ta∨TTafalse.So h must declareT¬Ta∨TTaneither true nor false.Because of the arbitrariness of h,all fixed points of σ1MdeclareT¬Ta∨TTaneither true nor false.Hence,T¬Ta∨TTais paradoxical in M according to the theory
(3.2)Consider the sentence¬T¬Ta∨¬TTa.Similar to(3.1),it can be prove that lfp(σ1M)declares¬T¬Ta∨¬TTatrue,and that¬T¬Ta∨¬TTais paradoxical in M according to the theory
(3.3)Consider the sentence¬Ta∨Ta.Since for any fixed point h of κM,h(¬Ta)=n,and h(Ta)=n, κM(h)(¬Ta ∨Ta)=n.Hence ¬Ta ∨Ta is paradoxical in M according to the theoryTlfp,κ.Let S be the unique ordinal-length sequence of hypotheses obtained in the construction of the least fixed point of σMaccording to Kripke’s inductive construction,where S0is the empty hypothesis. S is an increasing sequence of hypotheses.For every classical hypothesis h ≥S0, τM(h)must declare¬Ta ∨Ta true.So lfp(σM)declares¬Ta ∨Ta true.Therefore¬Ta ∨Ta is not paradoxical in M according to the theoryTlfp,σ.
(3.4)Consider the sentence ¬Ta ∧¬∃x(x= x).Since for any fixed point h of μM, h(¬Ta)=n,and h(¬∃x(x= x))=f, μM(h)(¬Ta ∧¬∃x(x= x))=n.h(¬Ta ∧¬∃x(x= x))= μM(h)(¬Ta ∧¬∃x(x= x))=n.Because of the arbitrariness of h,all fixed points of μMdeclare ¬Ta ∧¬∃x(x= x)neither true nor false.Hence ¬Ta ∧¬∃x(x= x)is paradoxical in M according to the theoryTlfp,μ.Since for any fixed point h′of κM,h′(¬Ta)=n,and h′(¬∃x(x= x))=f,κM(h′)(¬Ta ∧¬∃x(x= x))=f.Hence h′(¬Ta ∧¬∃x(x= x))=f.Hence¬Ta ∧¬∃x(x= x)is not paradoxical in M according to the theoryTlfp,κ.So□
Lemma 1.
ProofConsider a truth language L+without any nonlogical symbols except forT,quote names,a nonquote names a,and and a 1-place predicate symbol G.Let A be the sentence ¬T¬Ta∨¬TTa.Define sentencesTn(A)(n ≥0)as follows:T0(A)=A,andTn+1(A)=TTn(A).
Consider the sentence ∀x(GxTx)∧A.Let S be a revision sequence such that, S0declares ¬Ta,Ta and all elements in I(G)true,and declares ∀x(GxTx) ∧A false,and for any limit ordinal α, Sαdeclares both ¬Ta andTa true.6Note that both¬T a and T a are unstable up to α.The behavior of sentences in the set I(G) ∪{¬Ta,Ta,∀x(GxTx) ∧A} in S is shown in Table 1.Clearly, ∀x(GxTx)∧A is stably false in S.Hence∀x(GxTx)∧A ∧¬Ta is stably false in S.So ∀x(GxTx)∧A ∧¬Ta is not paradoxical in M according to the theoryT*.

Table 1
Lemma 2. Tlfp,σ24TC.
ProofLet a truth language L+have no nonlogical symbols except forT,quote names,countably many nonquote names an(n ∈N),and a 1-place predicate symbol G.Define sentences φ,ψn(n ∈N),An(n ∈N)and B as follows:
By compactness of classical first-order logic,the set{¬An| n ∈N}∪{¬B}is consistent.Hence there is a maximally consistent classical hypothesis h such that h declares all elements in I(G)and B false.Let S be a C-sequence where S0=h and for any limit ordinal α,Sαdeclares all elements in I(G)false.7Note that all elements in I(G)are unstable up to α and the set{A|A ∈Sent(L+)and A is stably true up to α in S}∪{¬A | A ∈Sent(L+)and A is stably false up to α in S}∪{¬An | n ∈N}is consistent by compactness of classical first-order logic.Hence such a C-sequence exists.The behavior of sentences in the set I(G)∪{B}in S is shown in Table 2.Clearly,B is stably false in S.So B is not paradoxical in M according to the theoryTC.
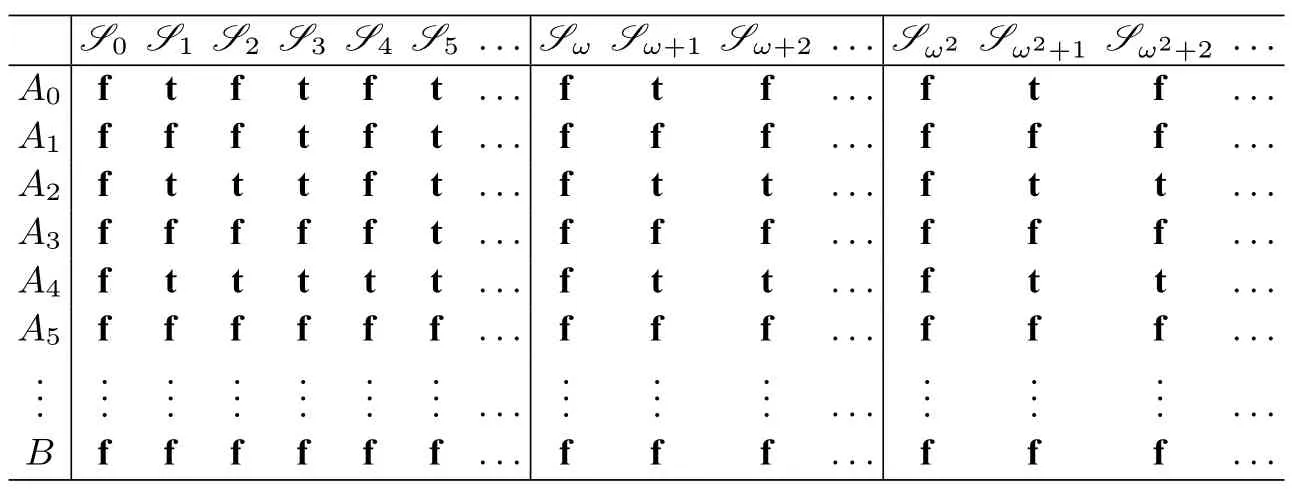
Table 2
Next,we prove that B is paradoxical in M according to the theoryTlfp,σ2.Given any C-sequence S′,by the definiton of An(n ∈N),it is not the case that,for any n ∈N, Anis stably true in S′.For similar reason,it is not the case that,for any n ∈N,Anis stably false in S′.In fact,for any n ∈N,Anis unstable up to any limit ordinal in S′.Next,we prove that for any fixed point h of σ2M,h delcares B neither true nor false.Note that for any revision sequence S,and any limit ordinal α,B is stably false up to α in S.Let h be a fixed point h of σ2M. h is strongly consistent.Let h′be a maximally consistent classical hypothesis such that h ≤h′and let S′be a C-sequence with=h′.It is easy to prove by transfinite induction that for every α,h ≤since σ2Mis monotone and agrees with τMon classical hypotheses.Let S1be the set{A | A ∈Sent(L+)and A is stably true up to ω in S′}∪{¬A | A ∈Sent(L+)and A is stably false up to ω in S′}∪{¬An| n ∈N}.Let S2be the set{A|A ∈Sent(L+)and A is stably true up to ω in S′}∪{¬A|A ∈Sent(L+)and A is stably false up to ω in S′}∪{An|n ∈N}.By compactness of classical firstorder logic,both S1and S2are consistent.There is a maximally consistent classical hypothesis h1such that h1declares all elements in S1true.And there is a maximally consistent classical hypothesis h2such that h2declares all elements in S2true.It is clear that h ≤h1and h ≤h2.However, τM(h1)(B)=f,and τM(h2)(B)=t.Hence σ2M(h)(B)=n.Then h(B)=n.So B is paradoxical in M according to the theoryTlfp,σ2.

Theorem 5.Figure 2 uses an arrow to represent that the relation ≤4holds between the theory at the start of the arrow and the one at the end of the arrow.When restricted to the three revision theories,the relation ≤4is the reflexive transitive closure of the relation shown in Figure 2.
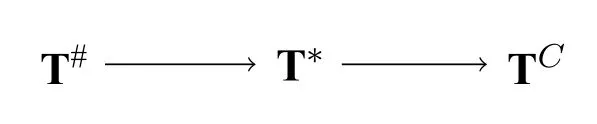
Figure 2
ProofSince ≤4is reflexive and transitive,it is enough to prove the following claims:(1)T#≤4T*,T*≤4TC;and(2)
(1)holds by Definition 2.
For(2),consider Example 5.7 in[5,p.387].From[5],we know that the sentences in Y are all nearly stably true in every revision sequence,but no sentence in Y is stably true in any revision sequence.Hence all sentences in Y are paradoxical in M according to the theoryT*,and all sentences in Y are not paradoxical in M according to the theoryT#.Therefore,is Lemma 1. □
Theorem 6.Figure 3 uses an arrow to represent that the relation ≤4holds between the theory at the start of the arrow and the one at the end of the arrow.The relation≤4is the reflexive transitive closure of the relation shown in Figure 3.
ProofGiven that ≤4is reflexive and transitive,Theorem 4 and Theorem 5,it is enough to prove the following claims:(1)TC≤4Tlfp,σ2;and(2)
The proof of (1)is as follows.Supposethen there is a truth language L+and a ground model M of L+and a sentence A ∈Sent(L+)such that A is paradoxical in M according to the theoryTC,and A is not paradoxical in M according to the theoryTlfp,σ2.Then there is a fixed point h of σ2Msuch that h(A)=torf.Let h′be a maximally consistent classical hypothesis such that h ≤h′.Let S′be a C-sequence with=h′.It can be proved by transfinite induction that for every α,h ≤given that σ2Mis monotone and agrees with τMon classical hypotheses.Hence,A is stably true or stably false in S′.Contradiction.Therefore,TC≤4Tlfp,σ2.
(2)is Lemma 2. □
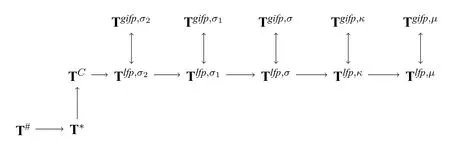
Figure 3
5 Conclusion
In this paper,we present a complete picture of comparing the thirteen theories of truth considered in Kremer’s comparative work([5]),according to the relation ≤4.In our comparison,we show that among the thirteen theories,the fixed-point theoriesTlfp,μandTgifp,μare the largest ones,and revision theoryT#is the least one,according to ≤4.
This paper extends Kremer’s comparative work by comparing these theories the perspective of paradoxicality.In the future,we will add more theories of truth to this comparative work,for example,five other revision theories considered in [8],including Gupta’s one in[2],Herzberger’s one in[4]and Yaqūb’s one in[10].
杂志排行
逻辑学研究的其它文章
- Analytical Research on the Expression of Argumentative Discourse from the Perspective of Generalized Argumentation—In the Example of Jack Ma’s Verbal Advocacy of 996 Work System*
- Reconstructive Deductivism and Its Misapplication
- Culture Merging:A Logic Based Method*
- Privacy in Arrow Update Logic*
- On Dimensions,Standard Part Maps,and p-Adically Closed Fields*
- A New Way of Defining Deductive Consequence for Modal and Predicate Logic
