善用转化思想 易于解决问题

范金祥

摘 要：《义务教育数学课程标准》指出：课程内容不仅包括数学的结果，也包括数学结果的形成过程和蕴涵的数学思想方法，转化是其中的思想方法之一，在数学的各个领域运用甚广，也是学生应当掌握的数学思想方法之一，所以，试从数与数的转化;形（体）与形（体）的转化;数形结合（数与形的转化）三个方面来说说小学数学教师可以怎样引导学生初步理解、掌握、应用转化思想方法来学好数学，解决问题。

关键词：小学数学;转化思想;解决问题

小学是学生学习数学的启蒙阶段，这个阶段让学生初步理解并掌握一些基本的数学思想实在重要。转化思想是数学思想的重要组成部分，它能将某些数学问题化新为旧，化难为易，巧妙地探索出解决问题的新方法。所以，我们在教学中应该引导学生理解、初步掌握转化思想，能用它去学习新知，分析、解决实际问题。

一、数与数的转化

将新学的一种数的计算变换成已经学会的一种数来进行计算，转化的方法用得多之又多，加减法计算中，以20以内的加减法为基础，100以内的加减法、多位数加减法、小数加减法、分数加减法都可以转化成已经学会了的数来进行计算。

以人教版三年级数学上册第37页例1为例，教师在引导学生列出算式271+122后说：“这是一道万以内整数加法算式，该怎么算呢？你想用什么方法来算出结果？”

生：用竖式计算。

师：竖式该怎样写？为什么？

生：写竖式时，数位要对齐，对齐数位就是对齐计数单位。

师：谁来具体说说什么意思。

生：个位上1（个一）加上2（个一）就是3（个一），个位上就写3，十位上7（个十）加上2（个十）就是9（个十），十位上就写9，百位上2（个百）加上1（个百）就是3（个百），十位上就写3。

师：哪位同学来说得简单点？

生：可以把271+122变成（转化）1+2=3（个一）、7+2=9（个十）和2+1=3（个百）三道简单的加法算式，只是写得数的时候，要注意写在他们各自的数位上。

学习例2（万以内进位加法，略）

师：我们将万以内的加法转化成20以内加法，大家来总结万以内的加法法则。

生：相同数位对齐，从个位加起，哪一位上的数相加满十，就向前一位进1。

师：通过本节课的学习，你有什么发现？

生：可以把万以内加法转化成20以内加法来计算，好简单！

看得出转化的方法給了学生学习的兴趣，成功的体验。

乘除法计算中，以表内乘除法为基础，多位数乘除法、小数乘除法都可转化为表内乘除法。分数除法可以转化成被除数乘除数的倒数。

二、形（体）与形（体）的转化

在学习几何图形的面积、体积计算时，将新的形、体转化成已经学会的形、体来解决的情况也非常多。

如“圆的面积”一课，课前教师可让学生准备好圆形纸片若干个、剪刀、直尺等学习用品。课上教师创设问题情境，让学生产生强烈的求出圆面积的愿望，又由于圆是曲线图形，一时无法求出面积，这时可启发学生：想想我们学过求平行四边形面积的方法和求圆周长的方法，大家能不能将圆转化成我们学过的图形，再进一步求出圆的面积。学生跃跃欲试，经过几分钟的小组合作与交流，各小组都已将圆通过切割成若干等分拼成了近似的平行四边形、长方形，甚至梯形、三角形……有的还推导出了圆面积计算公式S=πr2，这时，教师进一步引导学生明确：（1）为什么要转化成长方形，不转化成其他图形？转化成其他图形可不可以？（2）转化成的长方形面积和圆的面积是否相等？为什么？引导学生反思“转化”思想方法的精髓，是对形与形转化的又一次巩固与提升，也是为后面学习圆柱体转化成长方体做了充分的准备。

还有很多的图形面积、体积计算公式的推导也是如此，如将平行四边形转化成长方形，将三角形转化成平行四边形;将圆柱体转化成长方体;圆锥体转化成圆柱体。求长方体、正方体、圆柱体的表面积也运用到转化;一些组合图形的面积往往要通过剪、移、拼的过程，分解或组合成学过的图形，都是将新知转化成旧知。

三、数形结合（数与形的转化）

数形结合就是把抽象的数学语言、复杂的数量关系转化成直观的几何图形、位置关系，化抽象为形象，化复杂为简单，从而达到易于解题的目的。

数形结合对一年级的学生显得尤为重要，要解决“几加几”“几减几”……往往通过数手指头、数花朵、摆小棒等方法来实现“数”与“物”的对应，这“物”其实就是“形”的体现，这样就让学生对数学有了兴趣，有效地突破了解决问题的难点。

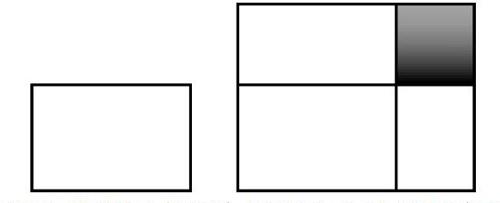
随着年级的升高，数形结合也在起着更大的作用，比如：种花大户王大伯，去年在一块长30 m，宽20 m的长方形地里种植玫瑰花，供不应求，今年想扩大种植面积，长和宽各增加15 m，问增加的面积是多少？有很大一部分学生出现这样的错误：15×15=225（m2）。为什么那么多孩子没有得出正确的解答，就是没有“数形结合”的意识，解决问题是凭感觉、想当然，没有养成动手画草图的习惯，如果能动手画一画，就会发现15×15=225（m2）只是增加面积中的一小部分（阴影部分），自然就会明白错误所在，也容易得出正确的解答。

这种画草图、线段图来解决问题的方法就是应用了数与形结合。因此，学生能否在用数形结合解决问题时，动手画一画草图的习惯，对于解决问题和学好数学是非常关键的。

总之，转化这种思想方法是数学内容的精髓，它应用于数学各个领域，自始至终伴随着学生，不管在哪方面，都是化新为旧、化繁为简、化抽象为具体、化无形为有形……从而巧妙地得出正确的解答。所以，教学中教师要结合具体教学内容，创设问题情境，引导学生初步理解、掌握、应用转化这种思想方法，才能有利于学生解决问题，有利于学好数学，更有利于激发学习兴趣、开发智力、培养能力。

参考文献：

林碧珍.数学思维养成课[M].福州：福建教育出版社，2018.

编辑 段丽君