新课程背景下初高中数学衔接教学的实践与思考

2020-12-23施雪平

新课程·上旬 2020年33期

施雪平

摘要：初中生在刚刚升入高中的时候，一下子不能快速适应高中阶段的数学教学模式，感觉数学知识的难度十分大，尤其是那些数学基础比较薄弱的学生，他们更是早早地丧失了学习的信心，进而成为学困生。现阶段高中数学教师亟须解决的一个问题就是如何有效衔接初中数学与高中数学，帮助学生融入高中数学学习。针对此，先阐述初中数学教学与高中数学教学之间存在的差异，接着提出相关衔接措施，最后详谈相关教学实践，以期为其他一线数学教师提供参考。

关键词：新课程;初中数学;高中数学;衔接教学

一、初高中数学教学差异的分析

1.教学环境与学习心理的变化

在教学环境方面，初中学生在进入高中以后，在一个陌生的环境中学习，需要一个较长的适应期。在学习心理方面，学生在经过了初三的紧张学习以及中考压力以后，步入高中校园不可避免会出现懈怠的情况，认为高中才刚刚开始，不需要那么紧张地学习;另外，还有部分学生受到家长以及周围人的影响，在心里一直认为高中数学很难，对数学学习也没有正确看待。

2.数学内涵的变化

在思维方面，初中数学知识对学生思维能力的培养仅在平面上，对学生逻辑思维的培养比较少。高中数学知识更为抽象，要求学生具有较强的逻辑能力、思维能力、想象能力以及解题能力，这样才能学好相关知识。在知识体系方面，随着新一轮教育改革的实施，高中数学教材也发生了一定改变，虽然难度都有一定降低，但是初中数学教材难度下降的幅度更大，而这样就导致高中与初中数学知识之间具有较大的跨度，学生在学习的时候难以快速融入课堂，进而学习难度也变得越来越大。

3.教学方法的变化

因为初中数学知识内容比较少，再加上充足的教学时间以及较慢的教学进度，所以教师有足够的时间反复讲解重点与难点知识，并且对相关习题的解题方法也有较好的示范，学生对知识的复习与巩固也更为充足。初中数学教师在讲完一种类型的习题以后，就会设计一些练习题，并让学生到讲台上演示。而高中数学知识量多，所包含的内容也较为广泛，所以教师在讲课的时候，多是从概念出发，然后将其中所包含的数学思想方法引出来，再加上高中时间少、任务重，教师难以做到对所有例题详细讲解，仅仅是有针对性地讲解典型例题，让学生做到举一反三，知识与能力同步提高。

二、新课程背景下初高中数学衔接教学的策略

1.掌握学生的基本学习情况

在学生刚刚步入高中的时候，教师要开展一次模拟测试，了解并掌握班级学生的知识基础以及学习情况;另外，教师还可以开展座谈会，了解学生的学习习惯，摸清初高中知识体系以及学生认知结构存在的差异。高中数学教师要在大纲与教材的基础上对高中数学知识的特点进行分析，找到重难点知识，如函数、集合等，然后从知识内容、学习方法、数学思想以及学习过程等各个方面考虑学生存在的学习困难。高中数学很多知识与初中数学有一定的衔接性，但有时也有很多知识推翻了初中所得到的结论，对此，教师要引导学生将新旧知识联系起来，尤其是那些容易发生混淆的知识，从而有效做到温故知新。

2.把握教材衔接点，精确教学

（1）有效利用教材已有衔接内容

随着新一輪教育改革的实施，初中数学教材与高中数学教材都进行了改编，都与学生的实际生活相联系，初中数学教材更为突出，其主要目的是对学生的创造能力以及解决问题能力进行培养。初中数学内容较简单，再加上趣味性较强，所以学生在学习的时候也感觉十分简单。而高中数学教材虽然难度有所下降，但是还有一定难度，再加上初中数学教师以及高中数学教师并不熟悉高中以及初中阶段的教材，这样就导致初高中数学知识相脱节，学生也跟不上课堂进度。在初中数学教材中，对一次函数、二次函数、一元一次方程、一元二次方程、二次函数的图象与性质等知识点有一定的涉及，并且要求学生可以利用函数、方程以及图象解决一些生活中简单的问题。这些知识分布在初中各个阶段，较为分散，学生在学习的时候也感觉较为简单。而高中数学必修一主要讲解的内容大部分就是函数，内容较为集中，具有较强的抽象性，导致学生在学习的时候感觉难度非常大。针对此，教师要深入挖掘教材，充分利用高中教材已有的衔接点开展课堂教学活动，帮助学生克服学习困难，提高教学效率。

（2）根据实际情况补充知识点

初高中数学知识存在极大差异性，但相互之间是有一定联系的。初中数学是高中数学的基础，它们两者是先后关系。如根与系数的关系，现在很多地区都将其拒之中考“门外”了，但是高中数学教师却以为学生对该知识点已经有较好的掌握，所以直接就将其应用到试题中，这样就导致学生经常出错，无法掌握该知识点。对此，高中数学教师要在了解学生实际学习情况的基础上补充相关知识点，如将根与系数的关系和韦达定理等相关知识补充到教学内容中，让那些没有学过该知识点的学生对该知识点进行学习，而对于学过的学生这就是重新复习巩固一遍该知识点，从而使学生更好地学习后期的知识点。

3.培养数学思维，衔接教学方法

初中学生的数学思维主要停留在形象阶段，而高中数学思维主要偏重于理论抽象思维，并随着知识的深入学习逐渐过渡到辩证思维。为此，高中数学教学要求学生在经过观察、分析、整理、归纳等过程后形成良好的数学思维，掌握数学知识。因此，高中数学教师必须在教学方法上有良好的衔接，具体如下。

（1）认真组织、开展教学活动，促进学生思维的过渡

初一数学知识的教学主要是对学生的抽象概括能力进行培养;初二数学教学主要是通过推理训练，促进学生形象思维能力的进一步发展;初三数学教学主要是开展解题活动，促进学生创造性思维以及预见性思维能力的进一步发展。而在高中数学教学中，教师要进一步加强对教学活动的组织与开展，并通过相关活动促进学生数学观念与数学思维的丰富。如在几何教学中，重点要对学生的辩证思维进行培养，因此，在初高中数学衔接阶段，教师要循序渐进，并通过科学、合理的教学活动促进学生思维能力的发展。教师需要注意，所涉及的教学活动一定要与学生的思维结构和认知水平相符合，同时也要确保教学活动的难度与强度。

（2）强化思维训练，对学生的联想转化能力进行培养

将复杂的问题转化为简单的问题是一种重要的数学思维方法，同时这种思维方法在高中具体教学中得到了广泛应用。众所周知，立体几何虽然是空间图形，但是在解答相关问题的时候还是要将其归结为平面几何来完成。如证明线面平行、线面垂直、线线平行、线线垂直、面面平行、面面垂直。

（3）重视知识归纳，促进学生逻辑思维的发展

科学、合理的知识结构可以为逻辑思维的发展提供帮助，使学生从单维逻辑向多维逻辑发展，进而形成完整的数学知识网络。在具体教学中，教师不仅要将教材知识良好地传授给学生，还要将归纳与整理的方法教授给学生，让其真正做到“由薄到厚”与“由厚到薄”。在复习数学知識的时候，要引导学生寻找各个知识之间存在的联系，形成清晰的知识结构图，使学生更简便、更清晰地学习、掌握、记忆相关知识。此外，教师还要引导学生总结思维方法与解题方法，并对其进行分类，找到它们相互之间存在的异同点，从而使学生形成独特的解题思维。

三、初高中数学衔接教学实践

以“任意角的三角函数”为例，开展相关教学活动，具体如下。

该知识点与初中“锐角三角函数”有一定的联系，而“锐角三角函数”又与之前学习的“勾股定理”和“相似三角形”有一定的联系，这就为高中“任意角的三角函数”知识点的学习奠定了基础。

以下是整堂课的教学设计：

1.教学目标：（1）理解任意角的三角函数定义;（2）根据定义可以判断各个象限的三角符号，并求出三角函数值;（3）理解锐角三角函数与任意角的三角函数定义之间的区别;（4）培养学生数

形结合的思想以及分析问题的能力。

2.教学难点：理解任意角的三角函数定义，判断各个象限的三角符号。

3.教学重点：对任意角的三角函数定义的理解与同化。

4.教学过程：教师可以通过问题先将之前所学的知识导入，让学生回顾锐角三角函数。

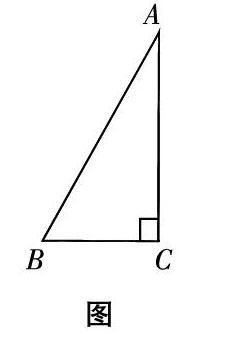
问题1：如下图RtΔABC中，∠A、∠B、∠C所对应的边分别是a、b、c，sinA= ;cosA= = ;tanA= = ？

问题2：一个锐角它的三种三角函数与直角三角形大小是否有关系，如果没有，那么它和谁有关系？对锐角三角形函数是如何定义的？

问题3：在ΔABC中，AB=7，BC=5，SΔABC=7，计算sinB。