一种新型介电弹性体仿生可调焦透镜的变焦分析1)
2020-12-23史惠琦王惠明
史惠琦 王惠明,†,2)
∗(浙江大学航空航天学院工程力学系,杭州 310027)
†(浙江大学浙江省软体机器人与智能器件研究重点实验室,杭州 310027)
引言
随着智能手机和相机产业的迅速发展,有关可变焦透镜的研究受到广泛关注.传统可变焦透镜系统的驱动要依赖电机和齿轮等调控装置,这会使整个系统变得笨重,导致无法在小空间内使用[1].人们在不断寻找小型化办法的同时,也在寻找其他更为有效的驱动调焦方式[2-12].介电弹性体驱动器(dielectric elastomer actuators,DEA)在这一领域显示出了巨大潜能.
介电弹性体薄膜在外加电场作用下能够在厚度方向产生收缩,并在面内方向扩展,从而产生较大的应变及作动力,具有超大变形、高弹性能密度、轻质量、低价格、易加工、易成形、高效率和短反应时间等特点[13-15],已被广泛应用于各种领域,如柔性机器人[16-18],能量采集器[19-20]等.其中,由介电弹性体驱动的可变焦透镜引起了广泛关注[21-23].与此同时,关于介电弹性体机电耦合行为和材料的非线性行为的理论研究也在不断深入[24-27],对基于此驱动方式的机电系统的设计和优化提供强有力的理论支撑和有效的分析方法.
最近,Li 等[28]设计完成了一款基于环状介电弹性体薄膜驱动的变焦透镜,结构如图1 所示,将两层圆形介电弹性体薄膜固定在框架上,上层膜涂覆了环形柔性电极,在两层膜和框架围成的空间区域内注入一定体积的盐水.当对涂覆了柔性电极的环状区域施加电压时,由于Maxwell 应力的作用[29],上层膜在厚度方向发生收缩变形,由于盐水体积不变的约束条件,驱动下层膜发生变形,从而导致整个透镜系统的光学性质发生改变.实验结果表明,将透镜的上下膜的半径设计成不相等,即图1(c)中ac,可以获得更加优越的光学性能.
本文建立了新近提出的一种新型高性能透镜的理论分析模型.利用上下两层膜的直径不相等的特点,可实现透镜在较大范围内快速调焦的功能.利用所建立的理论分析模型,模拟得到的光学性质(焦距变化率)随外界激励(电压)的变化,与实验结果相吻合.在参数分析中,讨论了影响透镜焦距变化的参数,如初始焦距、透镜的几何形状、预拉伸率、电极面积和膜的剪切模量等.
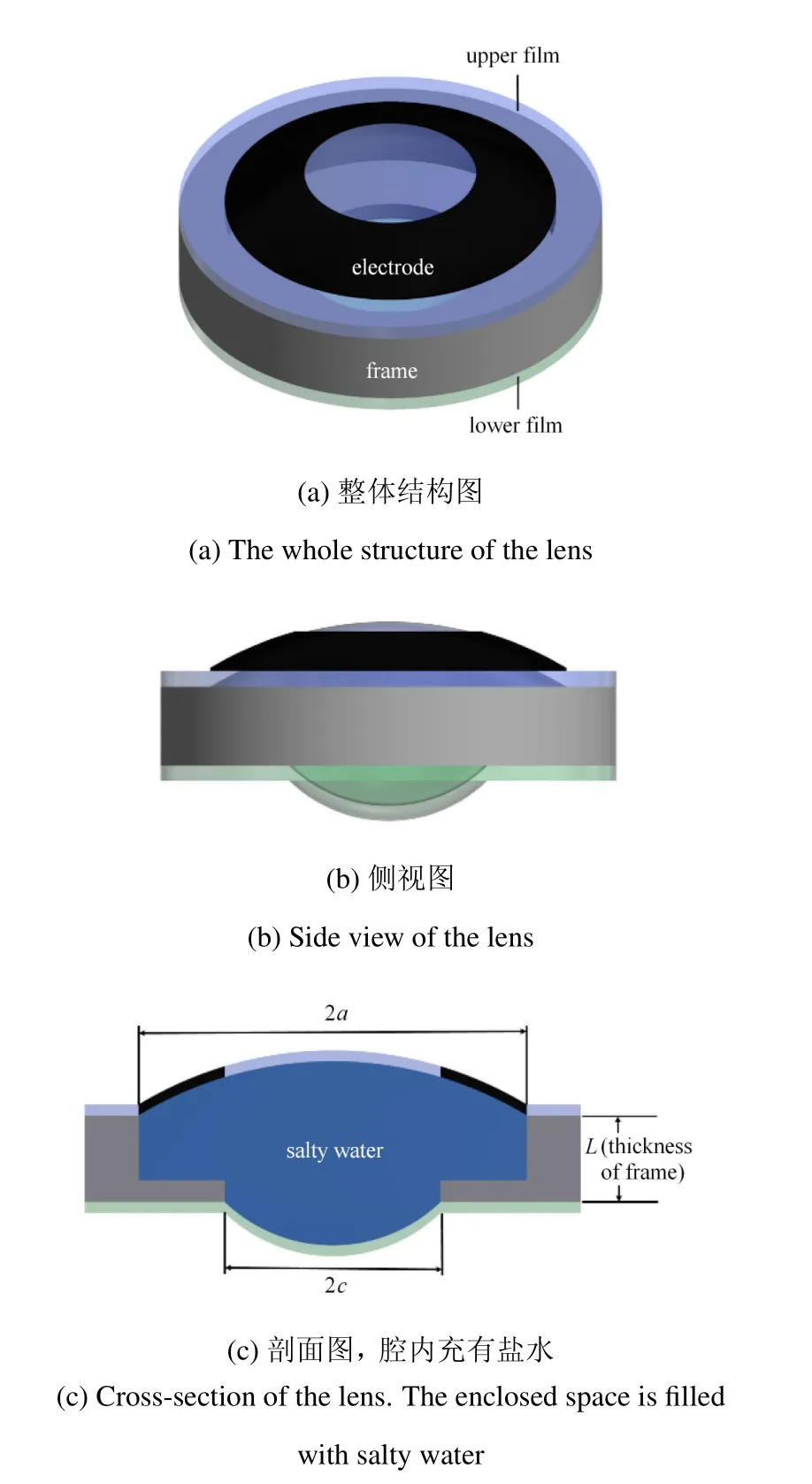
图1 仿人眼介电弹性体可调焦透镜示意图(上层和下层介电弹性体薄膜分别固定于半径为a 和c 的框架上,其中上层膜涂覆了环形柔性电极)Fig.1 Schematics of the biomimetic dielectric elastomer adaptive focus lens(The upper and lower dielectric elastomer films are fixed on frames with radius a and c,respectively.The upper film is coated with an annular electrode)
1 力学模型的建立
图2 给出了仿人眼介电弹性体可调焦透镜的力学模型,非线性分析模型的建立可参考文献[30-34].图2(a)表示参考状态,无外力和电压作用,薄膜上任意一点的位置用R表示.上层膜分为两个区域,即圆形透镜部分(0RB)和环形驱动部分(BRA),初始厚度为H.下层膜的半径为C,初始厚度为H.图2(b)表示预拉伸状态,上下两层膜分别被预拉伸后固定于半径为a和c的框架上.然后在上下两层薄膜和框架构成的封闭腔内注入体积为V0的盐水,设此时的液体压强为p0,见图2(c)表示的充液状态.图2(d)为驱动状态,在环形柔性电极的上下表面施加电压Φ,由于Maxwell 应力的作用,使得该部分薄膜的厚度减小,面积增大,这种机电耦合效应加上液体的耦合作用,导致所封闭腔体内液体压强由p0变为p,上下两层膜产生轴对称非均匀变形,引起透镜光学性质的改变.

图2 仿人眼介电弹性体可调焦透镜的力学模型(图中实心红色圆点表示处于参考状态时介电弹性体薄膜上距离中心点为R 的点在变形各阶段所处的位置. r-z 和r'-z'分别为上层膜和下层膜在现时构形中的坐标系)Fig.2 Mechanical model of biomimetic dielectric elastomer tunable lens(In each state,the position of a particular material particle is identified by a red dot. r-z and r'-z'are the coordinate systems of the upper film and the lower film in the current configuration,respectively)
采用坐标系(r-z)和(r'-z')来分别描述上下两层膜的变形,如图2(c)和图2(d)所示.利用非线性连续介质力学分析方法,考察在参考状态薄膜上距离中心点为R的点,在变形后,处于位置(r(R),z(R)),对应的参考状态距离中心点为R+dR的点,变形后占据位置(r(R+dR),z(R+dR)).两点之间初始长度为dR的线元变形后长度为λ1dR,λ1为径向伸长率,令θ(R)表示参考状态距离中心点为R的点在变形后该点的切线方向与水平方向的夹角,则

定义λ2为环向伸长率,有λ2=r/R.
当膜发生面外变形后,上层膜与r轴所在水平面包围的液体体积为


在恒温条件下,介电弹性薄膜变形的热力学系统,可用3 个独立的变量λ1,λ2,来表征,则Helmholtz 自由能密度W可表示为
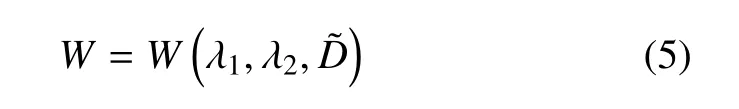
当介电弹性体处于平衡态时,自由能的增大等于机械载荷和电场做的总功,即
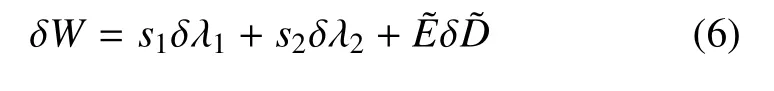
其中,s1为径向名义应力,s2是环向名义应力,是名义电场强度且有=Φ/H.
由式(5)和式(6)可得
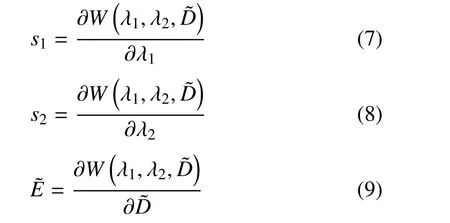
当自由能密度函数具体给定后,由式(7)∼式(9)可以确定出材料的本构关系.
利用变分原理,可以建立外边界固定且涂覆环形电极的介电弹性体薄膜的控制方程、边界条件和连续条件(具体推导见附录).用上标(1)和(2)分别表示中间圆形透镜部分(RB)和环形驱动部分(BRA)的物理量,则控制方程为
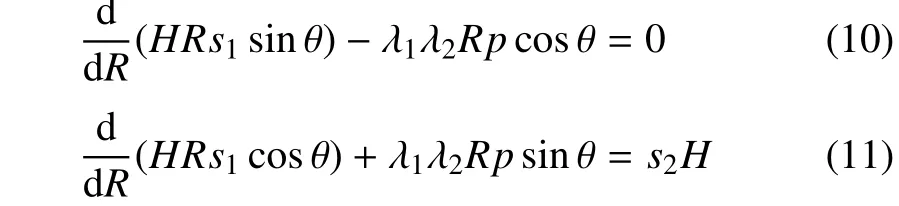
由于中间圆形透镜部分和环形驱动部分的控制方程在形式上完全相同,因此在式(10)和式(11)中略去了上标(1)和(2).对于上层膜,边界条件如下:
根据对称性,在透镜部分的中心位置(R=0)处
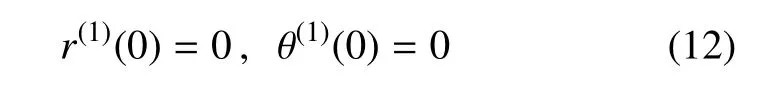
在膜的外边界处(R=A),有
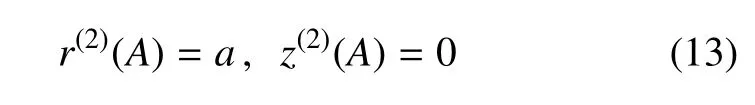
在两部分的连接处(R=B),有连续条件

对于下层膜,边界条件为
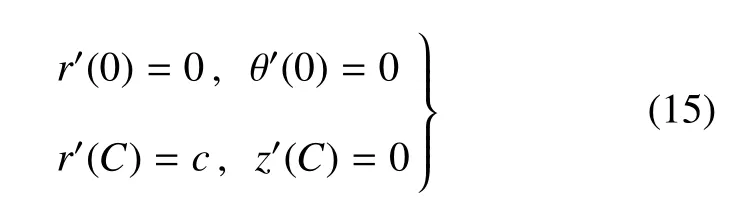
其中θ'代表下层膜任意一点在变形后切线方向与坐标轴r'的夹角.
2 本构关系
真实电场E和真实电位移间D存在线性关系D=εE,ε 是与材料变形程度无关的介电常数.假设介电弹性体薄膜具有体积不可压缩性质,所以厚度方向的伸长率λ3=1/(λ1λ2),名义电场与真实电场间的关系为E=λ1λ2,名义电位移与真实电位移的关系为D=/(λ1λ2),因此名义电场强度与名义电位移的关系有

将介电弹性体的自由能函数写成[35]

上式右端的第一项代表聚合物材料变形引起的弹性应变能函数,第二项是电场能量密度函数.采用neo-Hookean 模型,有
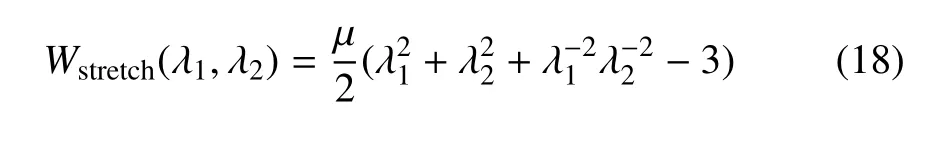
式中,µ代表聚合物材料在小应变时的剪切模量.将式(17)代入式(7)和式(8)得
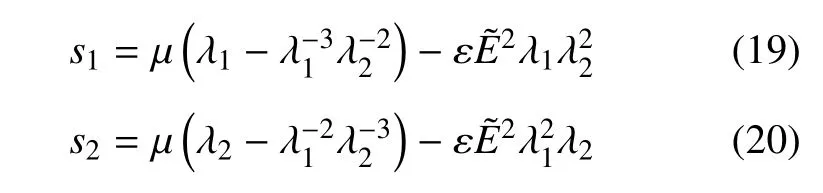
根据非线性连续力学理论,可建立名义应力与真实应力间的关系为σ1=s1λ1,σ2=s2λ2,即有

式(21)和式(22)中的第二项代表Maxwell 应力.对于没有涂覆电极的透镜部分和下层膜,在力学模型中只需设E=0 或=0 即可.
3 计算实现
由式(10)和式(11)可导出以下两式
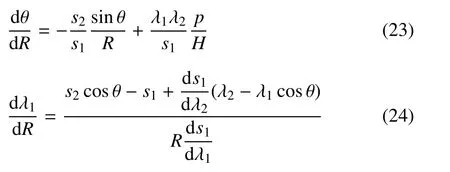
联立方程(1)和(2)以及方程(23)和(24),得到关于4 个函数r(R),z(R),θ(R),λ1(R)的一阶常微分方程组.
对于上层膜,中间圆形透镜部分(RB)无电压作用,令式(19)和式(20)中的=0,环形驱动部分(BRA)受电压激励,有=Φ/H.求解时采用打靶法,从中心点R=0 开始,利用边界条件(12)和(13),使用Matlab 中的fsolve 求解函数,利用介电弹性体薄膜在界面(R=B)处的连续条件(14),完成4 个物理量r(B),z(B),θ(B)和λ1(B)在界面处的传递,可得出最终的结果.对于下层膜,直接利用无电压作用情形的控制方程,结合边界条件(15),采用打靶法得到最终结果.
对于图2(c)所示的充液状态,将体积为V0的盐水注入两层膜之间的封闭的腔内,假设液体的压强,通过计算弹性场,利用式(3),可以确定出液体初始压强p0.当施加电压激励后,液体压强将发生变化,通过这种液体耦合作用,可驱动上下两层膜的变化,从而引起透镜光学性质的变化.采用双球面厚透镜公式计算透镜的焦距[36]
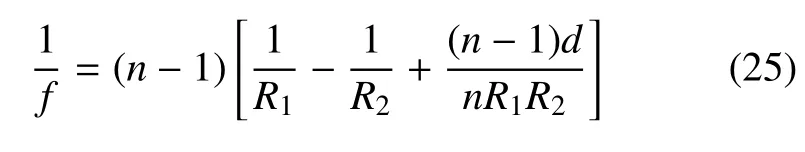
式中,n为透镜的折射率,数值计算中取为1.476[36].R1和R2分别为透镜两个表面的曲率半径,R1对应于近光源表面,此处为上层膜,R2对应于另一表面.d为透镜的厚度,即上层膜和下层膜两中心点之间的距离.本文在计算时使用了球面假设,当r(0)/a<0.3,|r'(0)/c|<0.3 时,即两层膜变形后中心高度较小时,可近似认为成两个球冠[36].
4 结果讨论
计算用到的参数见表1.另外,电极材料为碳脂,介电常数为4.16×10−11F/m.参数B/A.代表环形驱动部分的大小,值设定为0.4.首先将本文建立的理论模型计算结果与实验结果进行比对,根据表1 中的上下两层膜的参数和充液后的初始高度,确定出盐水体积为1210 mm3,初始焦距f0=17 mm,通过计算一系列电压驱动下透镜焦距的相对变化,将数值结果与文献[28]中的实验结果绘制于图3 中,两者吻合良好,表明本文的理论模型是有效的.理论模拟时考虑了拉力消失(loss of tension)的失效形式,即环向应力或径向应力减小到0 的情形.当达到拉力消失点后,薄膜将会出现褶皱,影响整体系统的光学性能,将无法正常工作.文献[28]中的透镜系统在5000 V 电压内工作,通过计算可知,在此电压范围内工作时,薄膜的最大电场强度远低于电击穿强度86 MV/m[37],因此后续的计算中可不考虑电击穿的失效形式.

表1 数值模拟中用到的材料及其参数Table 1 Materials and parameters of the lens used in_____________numerical simulation
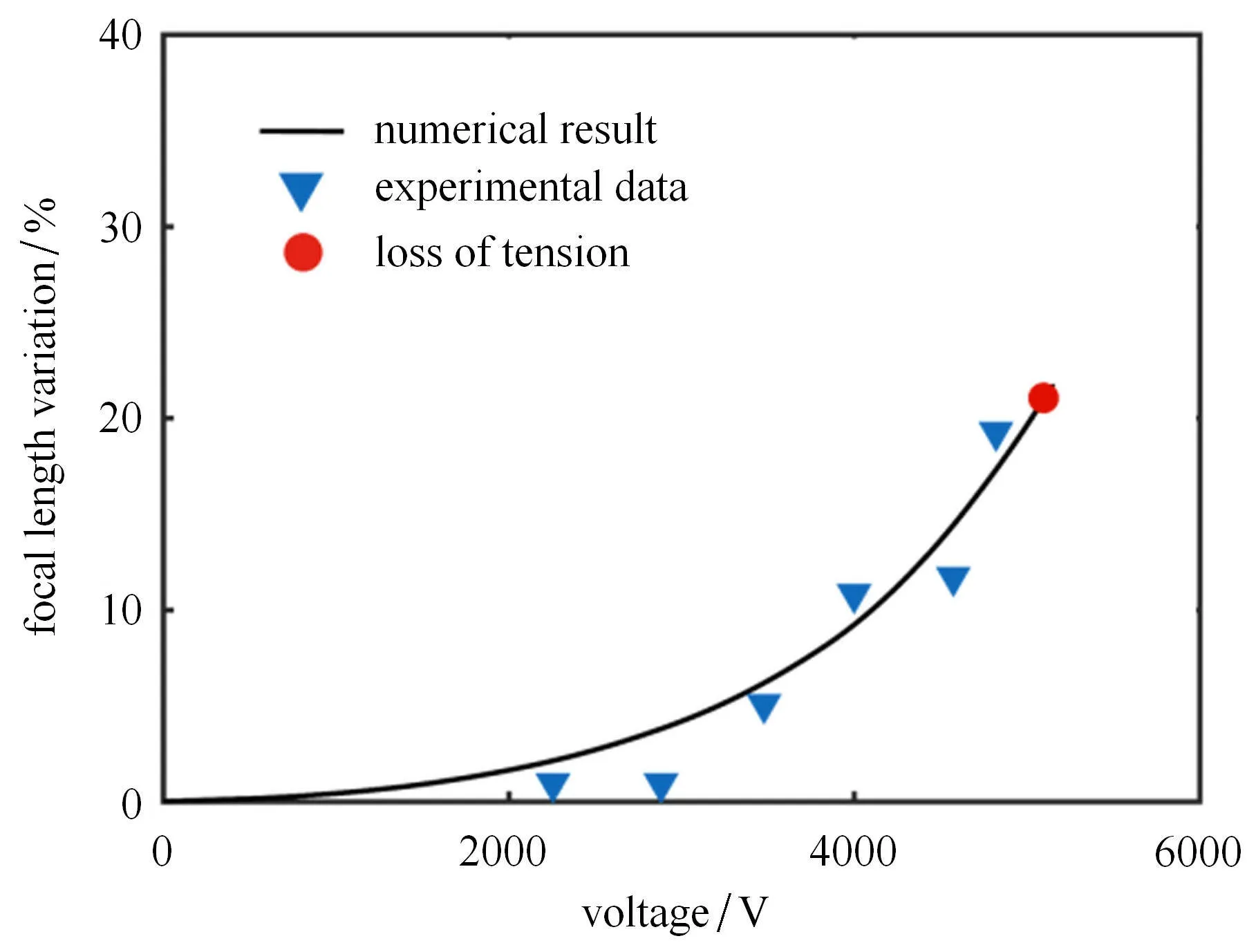
图3 本文模型的数值模拟结果与文献[28]中实验结果的对比(实心三角形表示实验结果,实心圆点表示拉力消失点)Fig.3 The comparison between the numerical results and the experimental data from Ref.[28](The filled triangles denote the experimental data.The solid circle corresponds to loss of tension)
图4 绘制了上下两层膜在不同电压下的形状改变及内腔压强改变.计算时使用无量纲量,电压的无量纲形式为,压强的无量纲形式为pA/(µH).通过观察图4(a)发现:随着电压增大,圆形透镜部分呈现出“下塌”形式,而环形驱动部分呈现出“外胀”形式,整体上层膜透镜部分形状的曲率半径由小变大,这是由于压强变小的结果,如图4(c)所示,因此曲率减小,且上层膜与中心平面包围液体的体积增大.图4(b)绘制出了下层膜的变形情况:随着电压变大,形状逐渐变扁,曲率减小,下层膜与中心平面包围液体的体积减小,但由于盐水体积的不可压缩特性,整个内腔中液体体积保持不变.随着电压的增大,压强下降速率增大,两层膜变化幅度也越来越大,且两层薄膜的位移方向均向对方方向移动,使得整体透镜厚度加速变薄,焦距加速增大.
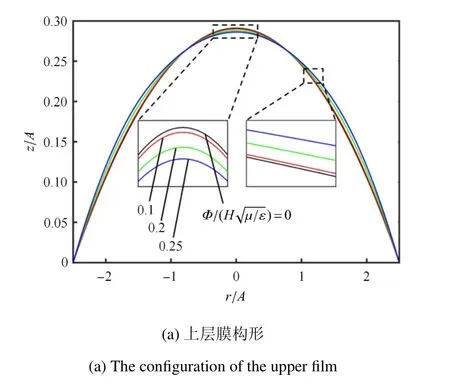
图4 介电弹性体薄膜在电压驱动下的构形图和液体压强的变化规律Fig.4 The configuration of the upper and lower films and the liquid pressure as a function of voltage

图4 介电弹性体薄膜在电压驱动下的构形图和液体压强的变化规律(续)Fig.4 The configuration of the upper and lower films and the liquid pressure as a function of voltage(continued)
图5 和图6 分别给出了上、下两层膜中径向、环向伸长率和真实应力以及电场强度的分布.在上层膜中,除环向伸长率λ2外,其他参数均在薄膜的无电极覆盖和有电极覆盖的连接处出现突变.连接处环向伸长率的连续特性可由连续性条件(14)的第一式获得,径向伸长率在连接处出现了突跳的行为,这一现象可解释为:介电弹性体的电致应变特性导致其在厚度方向变薄,在面内方向扩展,这一特性明显增大了驱动部分的径向伸长率,同时挤压无电极覆盖的区域,致使该区域的径向伸长率降低,施加的电压越大,这种现象越明显.由本构方程(21)和(22)可知,σ1和σ2在连接的界面处同样出现突跳的行为,其中环向应力的最小值出现在电极覆盖区域的内边界处,随着电压的增大而不断降低,此处将最先发生拉力消失的失效模式.图5(e)给出了无量纲电压和0.25 四种情形上层膜中的电场分布,结果表明,薄膜内的真实电场强度明显低于电击穿强度.
对于下层膜,由于液体压力的耦合作用,所给出的各物理场(径向和环向的伸长率和真实应力)均从外边缘到中心处呈现出单调增大的形式,在中心点处达到最大值,图6(a)和图6(b)以及图6(c)和图6(d)的计算结果表明,中心点处呈现等双轴拉伸状态.
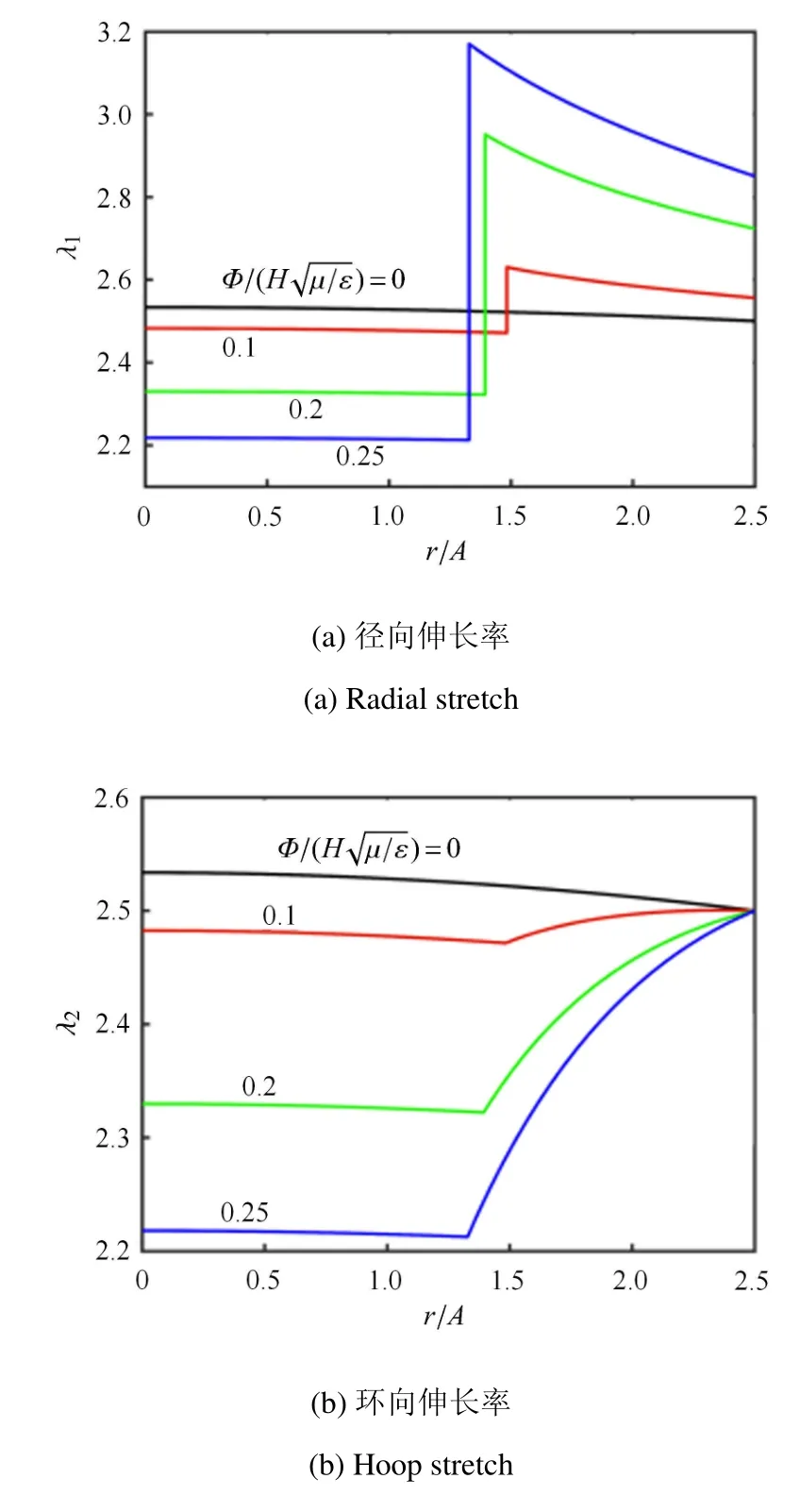
图5 上层膜发生非均匀变形时各参量的分布曲线Fig.5 Distributions of various quantities in the upper film with inhomogeneous deformation

图5 上层膜发生非均匀变形时各参量的分布曲线(续)Fig.5 Distributions of various quantities in the upper film with inhomogeneous deformation(continued)
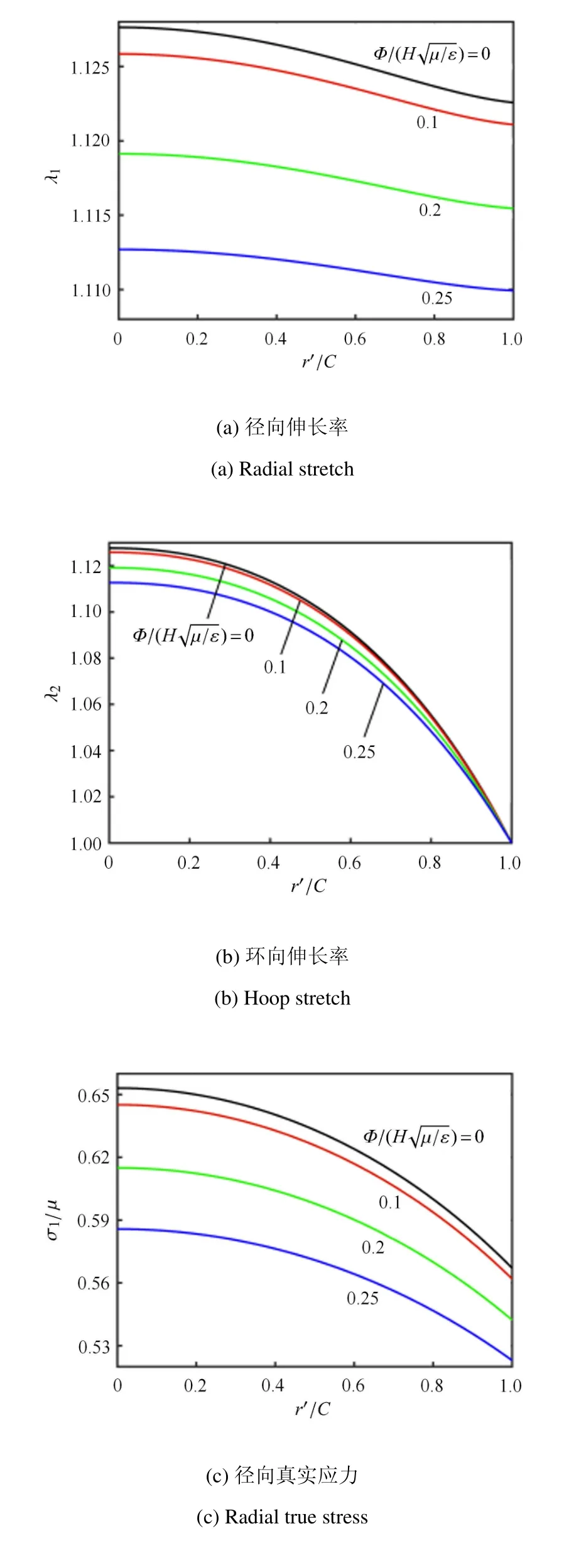
图6 下层膜发生非均匀变形时各参量的分布曲线Fig.6 Distributions of various quantities in the lower film with inhomogeneous deformation
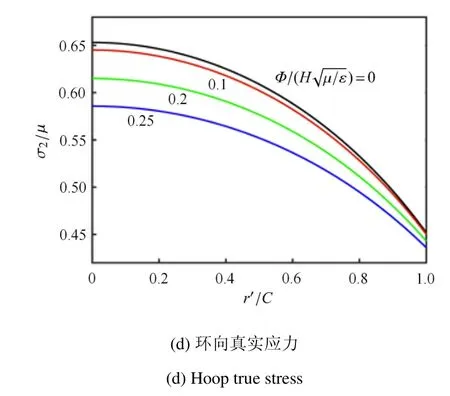
图6 下层膜发生非均匀变形时各参量的分布曲线(续)Fig.6 Distributions of various quantities in the lower film with inhomogeneous deformation(continued)
接下来利用本文建立的计算模型,开展透镜光学性质的参数分析,探究影响透镜焦距改变的各种途径.讨论了透镜的几何尺寸(上下窗口直径)、初始焦距、涂覆电极面积、上层膜预拉伸率以及下层膜的剪切模量等因素对焦距和焦距相对变化的影响.在图7 和图8 中,只标明改变的参数,其余参数均与原始透镜的参数保持一致(见表1),图8 中黑色曲线代表原始透镜的性能.
图7 给出了通过调整窗口半径a和c来改变透镜的焦距.图7(a)显示初始焦距随着透镜尺寸的整体变小而变小.此处的算例中,控制初始充液体积相等,对于尺寸较小的透镜,初始膨胀会增大.图7(b)显示了焦距的最大相对变化与透镜尺寸的关系.当固定a时,随着c增大,最大焦距相对变化率下降,当固定c时,随着a增大,最大焦距相对变化率增大,这是由于假设液体体积不可压缩的约束,上层膜形状的微小改变通过液体的耦合作用会引起下层膜相对大的变化,两者尺寸差距越大,此现象越明显.a/c是控制透镜性能的一个重要参数,也是采用类似结构的柔性透镜设计中一个必须考虑的问题[36].

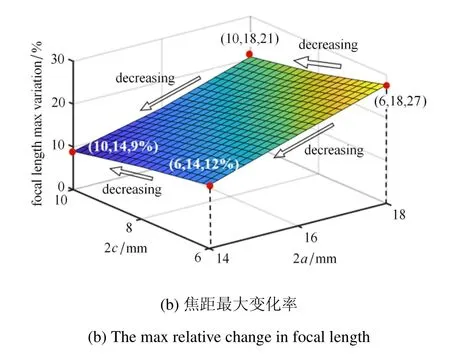
图7 可调焦透镜光学性质的变化规律Fig.7 Changes in optical properties of the DE soft tunable lenses

图8 可调焦透镜的参数分析Fig.8 Parametric analysis of the DE soft tunable lenses
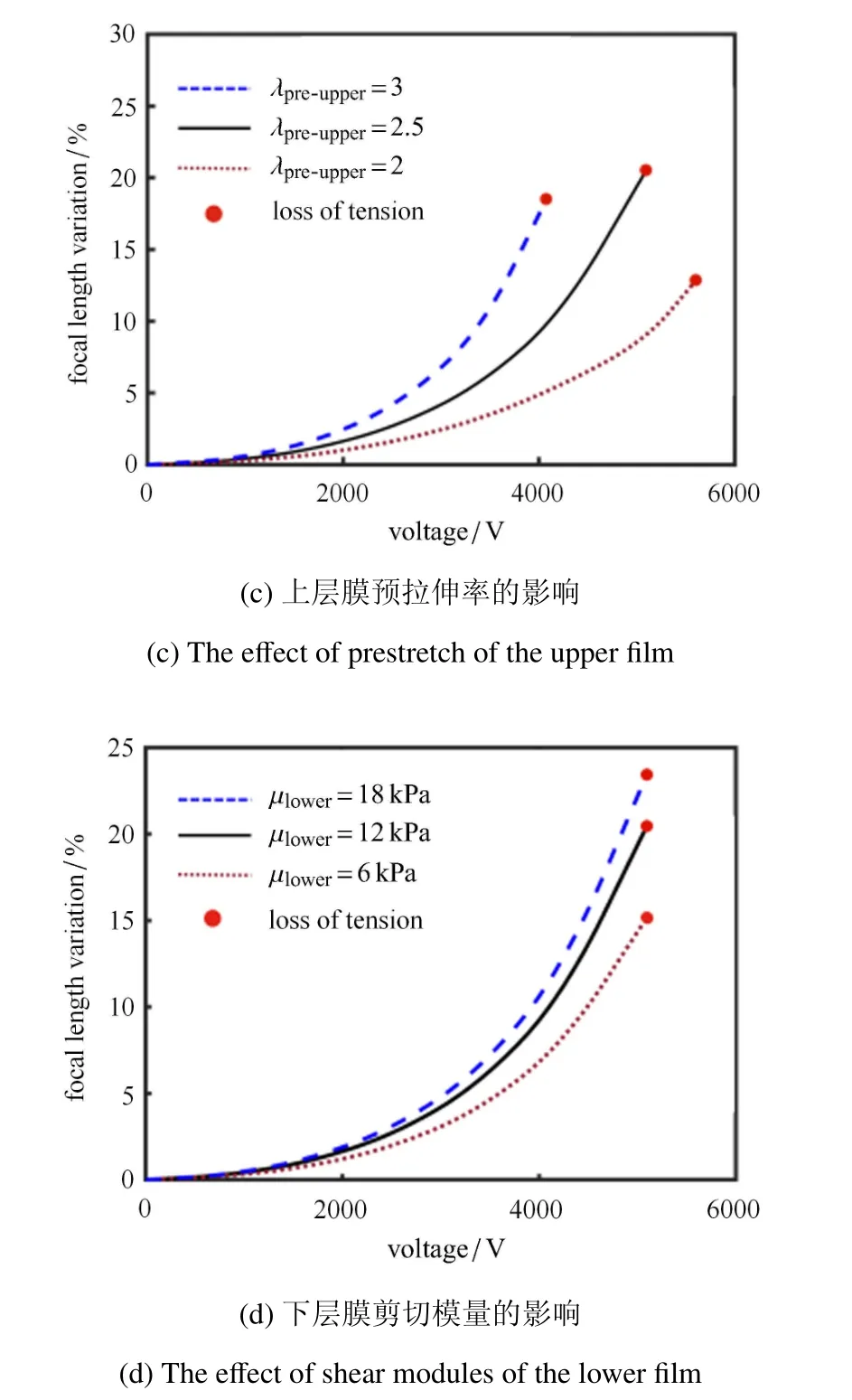
图8 可调焦透镜的参数分析(续)Fig.8 Parametric analysis of the DE soft tunable lenses(continued)
图8(a)给出了不同初始焦距f0对焦距相对变化率的影响.增大初始焦距(增加充液的体积)可略微提高光学可调性能,即在相同电压下可获得更大的焦距相对变化,但当液体体积过大时,系统整体质量和惯性增大,响应时间也会相应的延长,且液体本身的重量将对上下两层膜的变形造成一些干扰.图8(b)给出了涂覆电极面积对焦距相对变化率的影响.结果表明,涂覆电极区域面积越大(即B/A的值越小),在相同电压驱动下,上层膜与中心平面包围的液体体积增大量更多,由于液体体积的不可压缩性,下层膜的“收缩”会加大,故透镜焦距的可调性能增强.由于电极材料为黑色的碳脂,过度加大电极面积会影响透镜的透光性.文献[36]中报道了一种使用透明的碳纳米管做电极材料的光学透镜,结构与本文的类似,但采用的是全涂覆,即上层膜全部被电极覆盖.当使用全覆盖电极的结构时,透镜调节性能并非最佳,上层膜随着电压增大将不会出现图4(a)所示的中心部分“下塌”的现象,而是呈现整体均向上鼓起,与下层膜中心位置的移动方向一致,整体的调节性能会变差[32].图8(c)给出了上层膜预拉伸率对焦距相对变化率的影响.可观察到随着预拉伸率的增大,透镜焦距的可调节性能增强,但预拉伸率的增大,更容易引起拉伸破坏这一失效模式,这也是透镜结构设计中须考虑的问题.图8(d)绘制了下层膜剪切模量µlower(即下层膜的软硬程度)对焦距相对变化率的影响.当下层膜较硬时,充液后中心的凸起会降低,较软时情况相反.由图3 可知随着电压增大,焦距变化率越来越快,此时下层膜的中心突起也越来越低,即“扁平”形状的透镜更易受到电压的影响.
近些年,以介电弹性体电致变形机制而设计的驱动器受到了很大的关注,各驱动器的结构形式和驱动方式各有特色.文献[30]报导了一种仿人眼可变焦柔性透镜,其驱动方式是在透镜周边的DE 膜的厚度方向施加电压进行驱动.文献[31]中研究的介电弹性体驱动器,其下层膜圆形DE 膜上下表面是完全涂覆电极的.本文所研究的DE 可调焦透镜,是在一张圆形DE 膜的外圈涂覆环形电极,中间未涂覆电极的区域是透镜主体,通过在环形电极上施加电压进行驱动,这种结构和驱动方式使得透镜的调焦能力增强.理论分析中,在未涂覆电极的部分与涂覆电极部分的交界面处,涉及连续性条件的处理问题.
5 结论
本文建立了一种基于介电弹性体驱动的仿人眼柔性可变焦透镜的理论分析模型并开展了参数分析.这种透镜采用上下两层介电弹性膜固定在圆形框架结构形成封闭的腔体,并在腔体内充入一定量的盐水.该透镜结构的特点是在上层膜的上下表面涂覆环形柔性电极.在电极上施加电压驱动时,由于上层膜涂覆电极部分在膜的面内发生扩张而表现出外凸的效应并使得没有涂覆电极的中心区域的膜呈现出“下塌”的效应,又利用液体的耦合作用,使得下层膜向上层膜方向靠近,可实现透镜焦距的高效调节.
利用建立的理论模型,本文的模拟结果跟实验结果吻合良好.在利用打靶法求解薄膜的物理场时,高效地处理了薄膜在涂覆电极和未涂覆电极的界面处的连续条件.开展了影响透镜焦距变化的参数分析,如初始焦距、透镜的几何尺寸、预拉伸率、电极面积和剪切模量等因素.此模型可为的柔性透镜设计提供理论指导,进一步的研究可开展透镜的动态性能分析.
附录
采用虚功原理推导上层膜的控制方程和连续条件.在平衡状态下,对于微小的扰动,系统的Helmholtz 自由能的增加应等于外界激励做的功
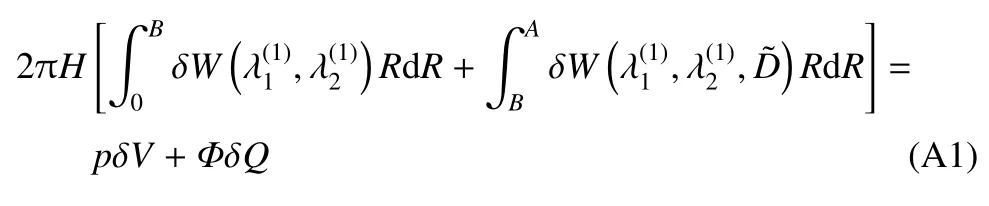
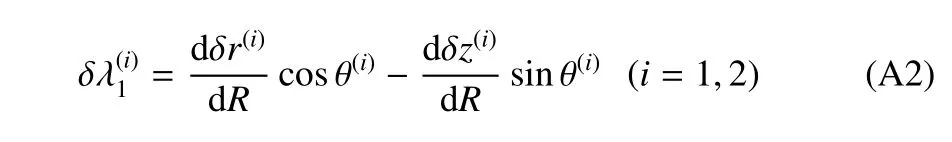
环向拉伸率变分为

将δr(i)和δz(i) (i=1,2)和作为独立变量,利用式(5)∼式(8)以及式(A2)和式(A3)可得
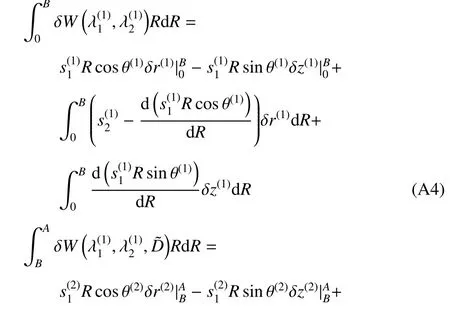

液体压力做功为
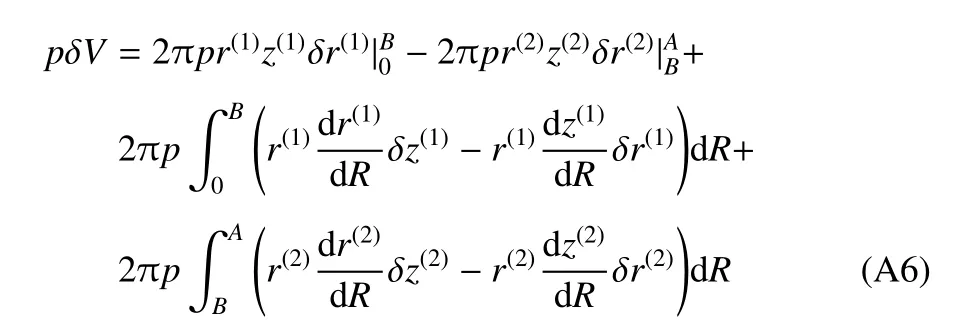
电场力做功为
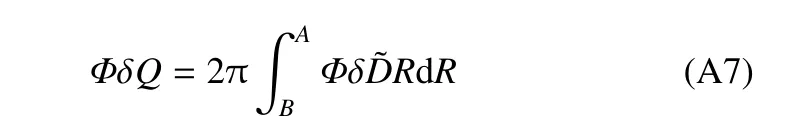
将式(A4)∼式(A7)代入式(A1),并利用式(A2)和式(A3),可得到如下控制方程(其中i=1,2)
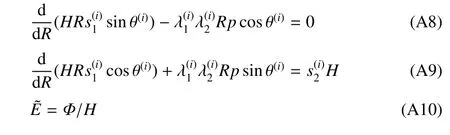
和连续条件
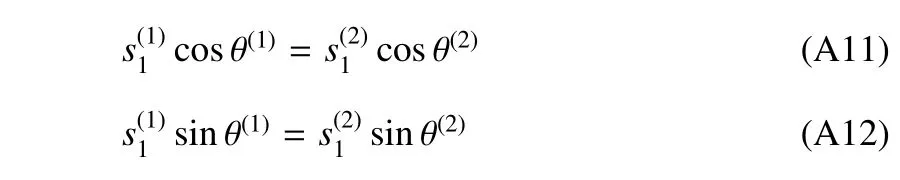
由式(A11)和式(A12)可进一步得到

