基于机动目标滤波估计的航天器主动规避策略1)

李皓皓 张进 罗亚中

(国防科技大学空天科学学院,长沙 410073)

引言

近年来,航天器操控技术日新月异.面向空间大型柔性结构[1]、多体系统[2]以及大型空间结构在轨组装[3]等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向,其优劣直接影响逃逸器的生存能力.因此,规避策略的研究是逃逸器主动规避的核心问题.

航天器相对导航是空间近距离操作任务的基础[4].逃逸器的规避策略同样离不开对追踪器状态的估计.当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5].最简单的目标机动模型是白噪声加速度模型,也叫匀加速模型,它假设目标做匀加速运动,将目标加速度变化量建模为白噪声.Singer[6]于1970 年提出了著名的Singer 模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer 模型的基础上提出了当前统计模型[7],其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度.目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8].本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取.

逃逸器的规避策略目前已有较多研究[9-10],主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli 等[11]构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值,以此为施加机动方向.此外,Wang 等[12]、郑重等[13]通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14].张秋华等[15]在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16]采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17]采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18-19]研究了相对运动对系统可观测性的影响,设计系统可观测度,以此为优化目标对最优规避进行了求解.沈红新等[20]考虑了航天器质量变化,将三维追逃问题拓展为28 维,采用间接打靶法求解了鞍点.李振瑜等[21]在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong 等[22]通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题.此外,Shima 等[23-24]研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25],即逃逸器已知追踪器的相对位置、速度等控制输入量,然而对于非合作航天器,这些信息是无法实时已知的,因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息,且状态信息具有一定误差.

追踪器的追踪策略(主要体现为追踪制导率)同样是追逃问题的关键因素,然而本文主要研究逃逸器的规避策略,因此采用经典的比例导引律(proportional navigation) 作为追踪器的制导率.比例导引律具有简单、高效而且易于工程实现的特点,广泛应用于导弹拦截、空间交会问题[26-28].本文主要研究在追踪器采用比例导引律接近逃逸器,追逃双方信息不透明的情况下,逃逸器基于当前统计模型自适应滤波算法对追踪器状态进行滤波估计,同时最大化视线转率以降低追踪器制导率作用的航天器主动机动规避策略.

1 机动目标滤波算法

1.1 相对导航观测模型

由于追逃双方采用相同的机动目标滤波算法获取相对状态,因此本文以逃逸器为例进行说明.以逃逸器质心为原点建立VVLH 相对导航坐标系Oc-xyz,其中Oc-x轴指向逃逸器V-bar 方向,Oc-y轴指向逃逸器−H-bar 方向,Oc-z轴指向逃逸器−R-bar 方向.相对导航测量量为相对距离和相对角位置.在VVLH 坐标系中对相对角位置进行定义,如图1 所示,定义追踪器相对于逃逸器的视线方向与导航坐标系中xy平面的夹角为俯仰角α ∈(−π/2,π/2),视线方向在xy平面的投影与x轴方向的夹角(从x轴开始沿逆时针方向度量)为方位角β ∈(−π,π).

在上述定义下,逃逸器对追踪器进行观测可得观测方程为

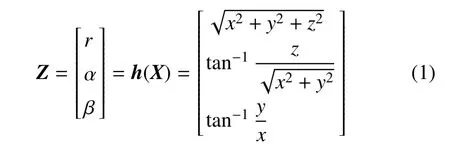
其中,X为位置、速度和加速度等状态变量,X=[x,y,z,vx,vy,vz,ax,ay,az]T,对应的观测敏感性矩阵为

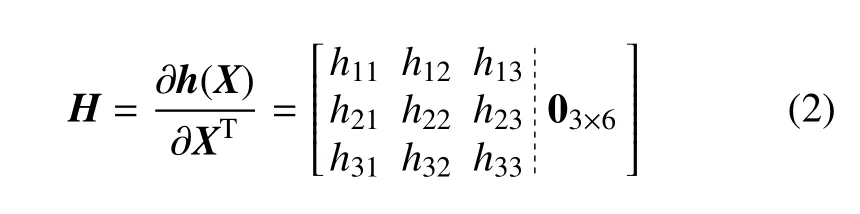
其中,观测敏感性矩阵H的各分量表达式如下

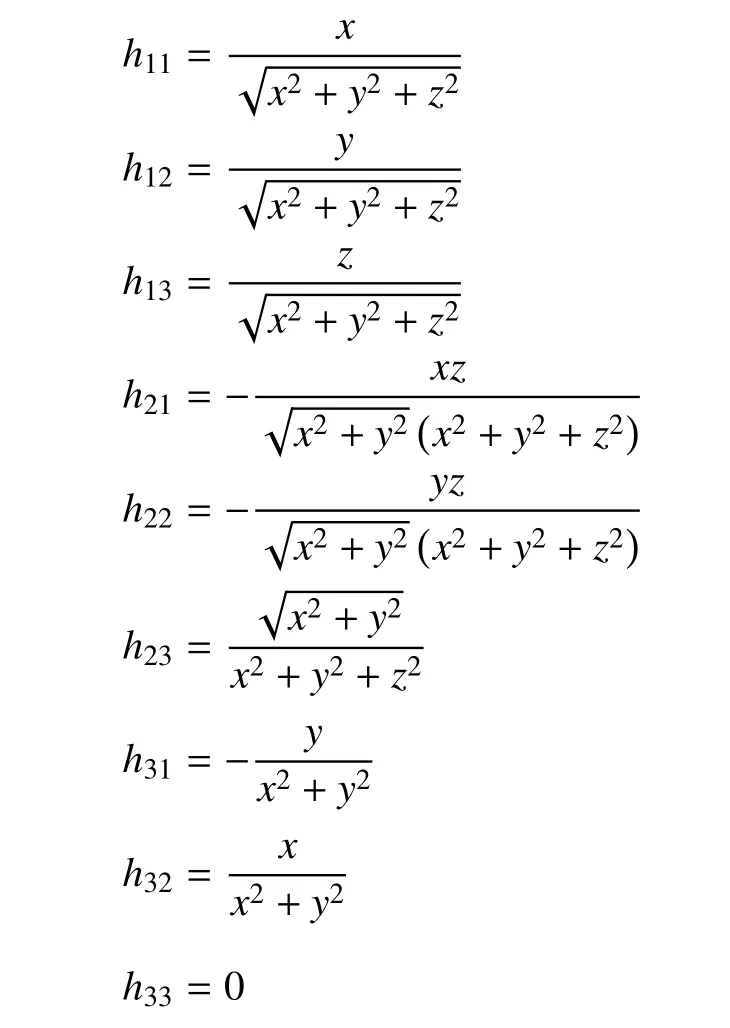
1.2 基于当前统计模型的自适应滤波算法

逃逸器对追踪器的跟踪滤波是空间三维过程,为便于表达与论述,以x方向为例进行公式推导.考虑加速度均值非零的时间相关模型,x方向的动力学方程为

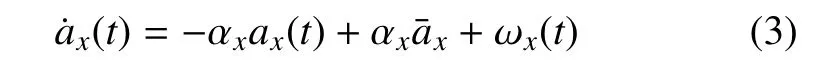
其中αx为根据经验设定的机动频率.令Xx(t)=[x(t)vx(t)ax(t)]T,根据式(3)建立滤波状态方程如下

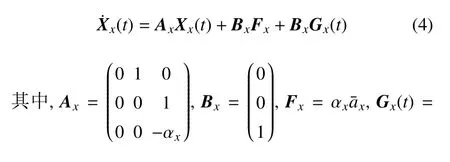
令Xx(k)=[x(k),vx(k),ax(k)]T,可得离散状态方程为

令Nx(∆t)=e[(k+1)∆t−τ]AxBx,则Gx(τ) dτ,Wx(k) 为离散时间白噪声序列,即E[Wx(k)(k+j)]=0(∀j0).由噪声Wx(k)可求得系统误差协方差矩阵为

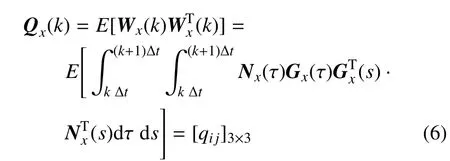
Qx(k)=[qij]3×3的具体表达式限于篇幅不再详细给出.

根据当前统计模型的意义,将a(k) 在滤波流程中的一步预测值a(k+1|k) 看作在k∆t时刻瞬时的当前加速度,即随机机动加速度的均值,便可得到加速度的均值自适应算法,即设=ax(k+1|k).此时,将加速度的瞬时均值代入卡尔曼滤波公式Xx(k+1|k)=Φx(k+1,k)Xx(k|k)+Ux(k),便可对状态转移矩阵Φx(k+1,k)进行化简,得到均值自适应的状态转移矩阵

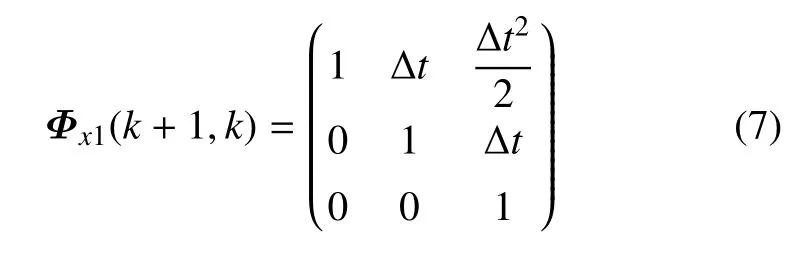
此时,状态转移方程简化为Xx(k+1|k)=Φx1(k+1,k)Xx(k|k).

考虑y与z方向时,公式推导是类似的,注意此时X(t)=[x,y,z,vx,vy,vz,ax,ay,az]T,F=[αx,αy,αz]T,G(t)=[ωx(t),ωy(t),ωz(t)]T,加速度均值ā 仍然为滤波流程中的一步预测值a(k+1|k).按照同样的步骤进行积分即可.值得注意的是,此时系统误差协方差矩阵Q(k)的推导为

Q(k)为9×9 的矩阵,具体表达式限于篇幅不再详细给出.

2 主动机动规避策略设计

假设追踪器采用比例导引律对逃逸器进行追踪接近,比例导引律的原理在于抑制追踪器相对于逃逸器的视线偏转,使追踪器一直对准逃逸器.逃逸器想要通过机动规避追踪器的接近时,可以通过施加适当方向的加速度使视线偏转率最大,限制追踪器机动的作用,使脱靶量最大从而达到规避的效果.

2.1 追踪器比例导引制导指令加速度

为便于描述视线偏转和构造制导指令加速度,建立视线坐标系.以追踪器质心为原点,X轴指向视线方向,Y轴在轨道面内垂直于X轴,Z轴与X,Y轴构成右手系.按照此定义,易知惯性系首先绕Y轴旋转qβ角,再绕Z轴旋转qε角,便可得到视线系.因此,视线系的xA,yA,zA三个坐标轴方向可表示为

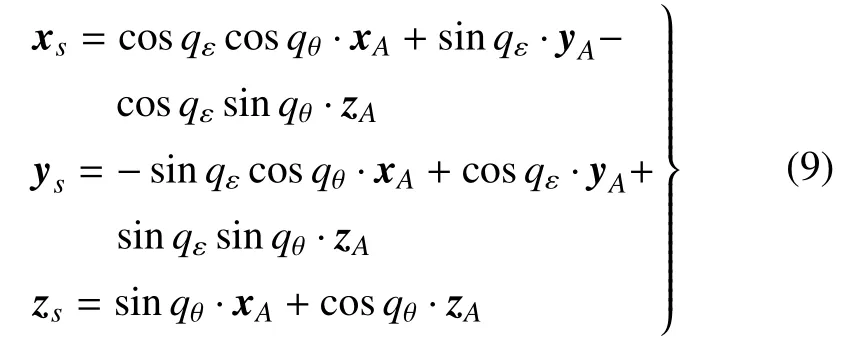
三维比例导引律在视线坐标系内的指令加速度为[29]

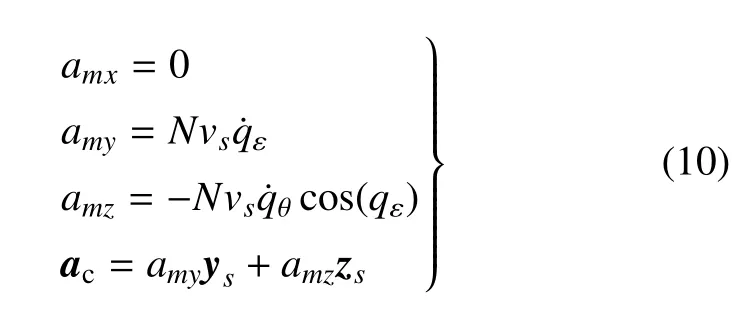
2.2 逃逸器追踪器视线角及视线角速率

在视线坐标系中,视线角qε和qθ以及视线角速率和可用以下公式计算[29]

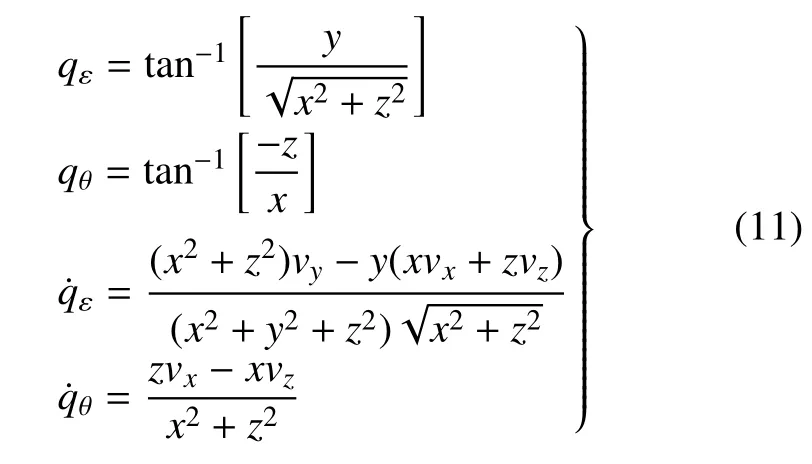
其中,(x,y,z) 表示追踪器相对于逃逸器的位置,(vx,vy,vz)表示追踪器相对于逃逸器的速度.

2.3 主动规避控制加速度

追踪器采用比例导引率对逃逸器进行追踪接近,逃逸器采用测角加测距的测量方式,考虑空间中测角和测距的测量误差,采用当前统计模型对追踪器进行滤波分析,得到追踪器在VVLH 坐标系中的位置()、速度() 等滤波信息,将其转换到惯性系.假设逃逸器自身的位置()、速度() 已知.通过惯性系中的导航数据,根据式(10)和式(11)计算追踪器当前的指令加速度方向,以此为逃逸器当前的逃逸方向.则逃逸器的制导加速度为

其中,aNt为逃逸器的最大推力加速度,即逃逸器始终以最大加速度进行机动.

3 算例分析

3.1 问题配置

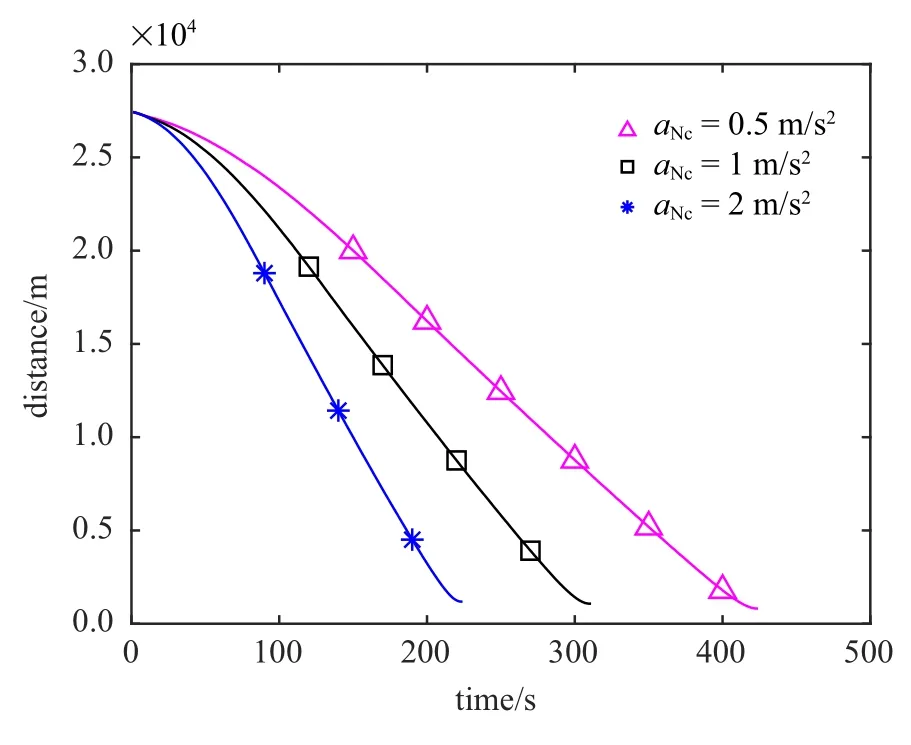
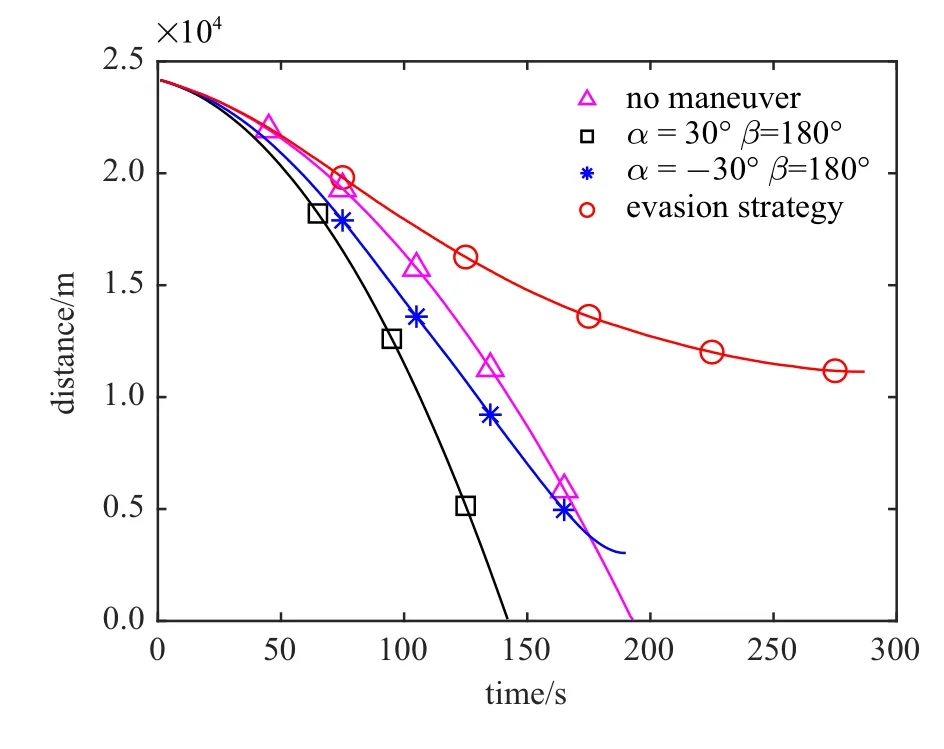
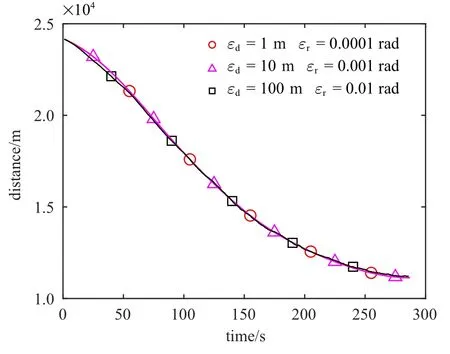
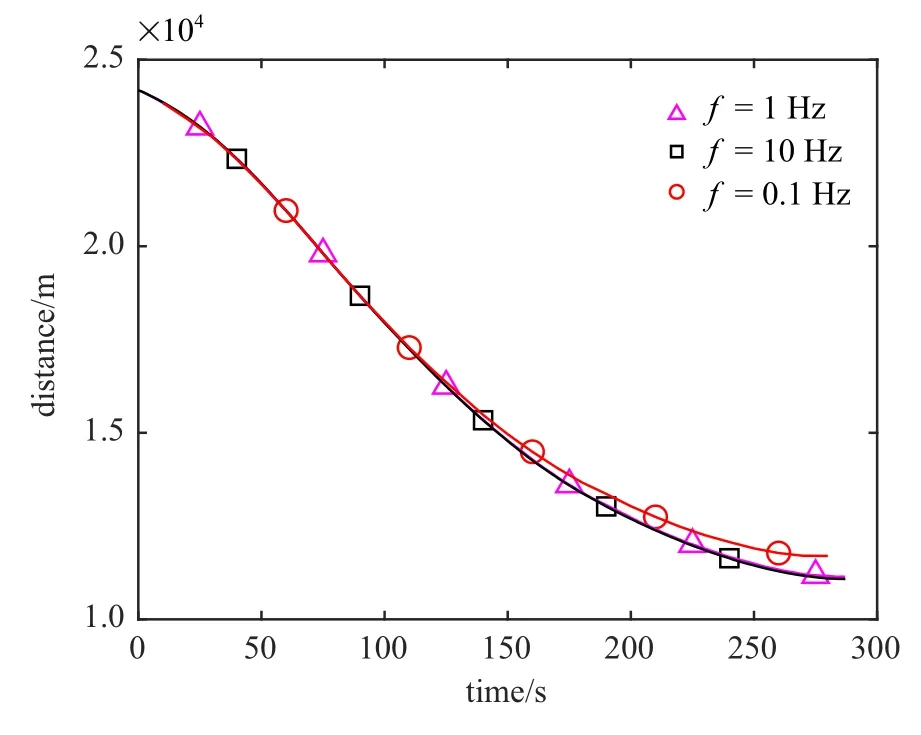
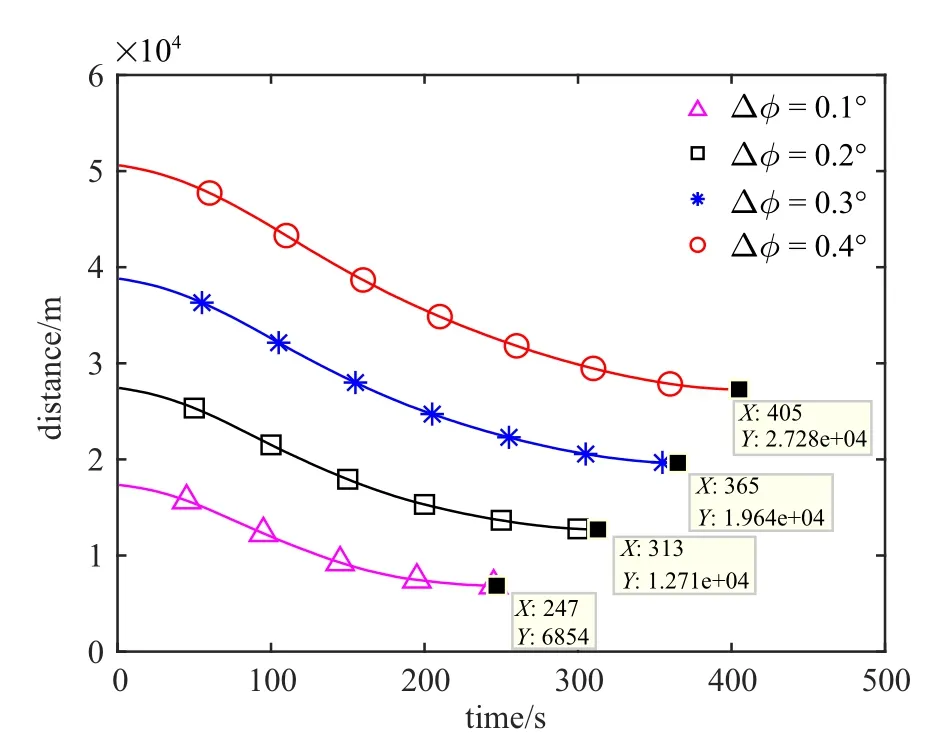
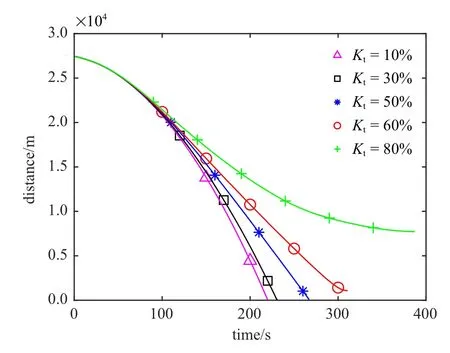
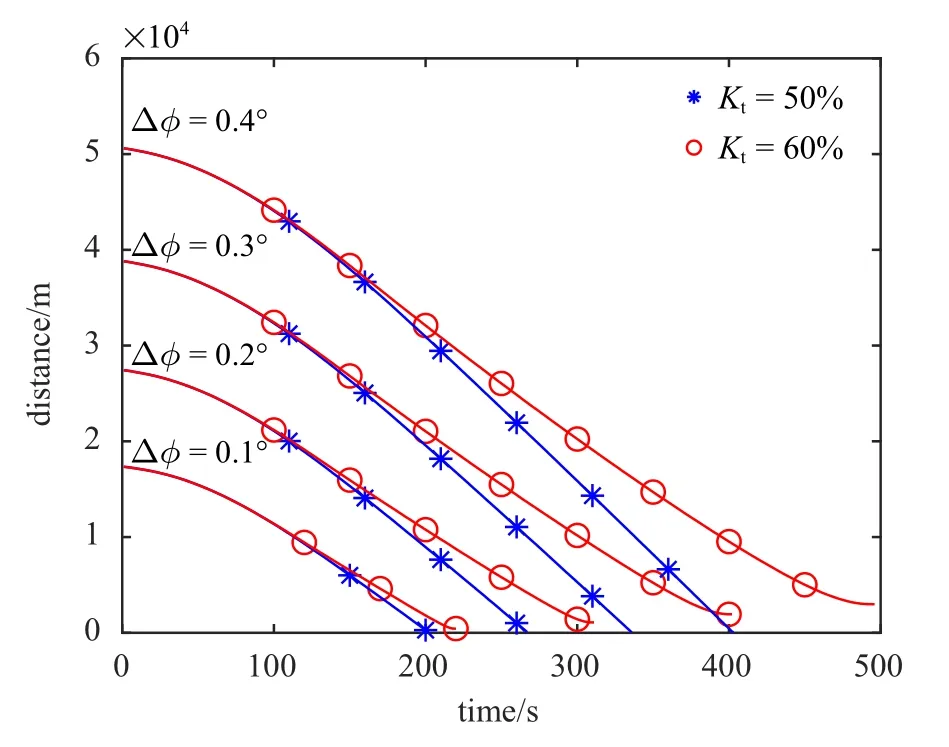
逃逸器的初始轨道根数如表1 所示,逃逸器采用光学相机和激光测距仪对追踪器进行测量,可以获得相对距离、俯仰角和方位角.当前统计模型中,x,y,z三个方向的机动频率设为αx=αy=αz=0.001 Hz,滤波最大加速度设为1.8 m/s2.定义逃逸器的安全距离d=100 m,当追踪器与逃逸器之间的距离|r|

表1 逃逸器轨道根数Table 1 The orbit elements of escaper

3.2 仿真分析

本文首先验证提出的规避策略的有效性,然后从观测设备(光学相机、激光测距仪) 的测量精度、工作频率、逃逸器与追踪器的初始状态、逃逸器的机动能力等方面进行敏感性分析,以保证仿真的全面性和可靠性.

3.2.1 规避策略有效性验证

设光学相机的角度测量误差标准差为 εr=0.001 rad,激光测距仪的距离测量误差标准差为εd=10 m.光学相机和激光测距仪的工作频率设为f=1 Hz.在以逃逸器质心为原点的VVLH坐标系中,追踪器相对于逃逸器的位置为rrel=[−21 000 m,0 m,12 000.0 m]T,速度为vrel=[23.0 m/s,0 m/s,−14.0 m/s]T.逃逸器的最大推力加速度为aNt=1.0 m/s2,追踪器的最大推力加速度为aNc=1.05 m/s2.为有效分析提出的规避策略的有效性,设计以下4 组对比工况:(1)逃逸器不机动;(2)逃逸器按照固定方向机动(α=30◦,β=180◦);(3)逃逸器按照固定方向机动(α=−30◦,β=180◦); (4)逃逸器按照最大化视线偏转率的主动规避策略进行机动.

仿真结果如图2 所示,其中,横轴表示仿真时间,纵轴表示追踪器相对于逃逸器的距离(下同).

图2 规避策略有效性验证Fig.2 Validation of evasion strategies

由图2 可知,逃逸器不机动时,追踪器在193 s 成功接近逃逸器;逃逸器按照α=30◦,β=180◦的固定方向机动时,追踪器在142 s 成功接近逃逸器;逃逸器按照α=−30◦,β=180◦的固定方向机动时,追踪器无法接近到逃逸器的安全距离以内,在190 s 时,追踪器与逃逸器视线方向的相对速度变为大于0 时,发生脱靶,此时追踪器与逃逸器的相对距离为3 038 m;逃逸器按照机动规避策略进行机动时,追踪器无法接近到逃逸器的安全距离以内,在287 s,追踪器与逃逸器视线方向的相对速度变为大于0 时,发生脱靶,此时追踪器与逃逸器的相对距离为11 142 m.综上分析,最大化视线偏转率的主动规避策略可以有效提高逃逸器的生存能力.

3.2.2 测量精度敏感性分析

分析光学相机和激光测距仪的测量精度对规避策略的影响.设计三组对比工况,角度测量误差标准差εr和距离测量误差标准差εd分别为(1)εd=1 m,εr=0.000 1 rad; (2) εd=10 m,εr=0.001 rad;(3) εd=100 m,εr=0.01 rad.其余参数设置与3.2.1相同.仿真结果如图3 所示.

由图3 可知,测量精度下降导致滤波精度下降,εd=100 m,εr=0.01 rad 对应的曲线不如其余两种情况平滑,但是逃逸器规避机动的效果并无明显区别,即说明规避策略对观测设备的测量精度不敏感.

图3 测量精度敏感性分析Fig.3 Measurement accuracy sensitivity analysis

3.2.3 工作频率敏感性分析

分析光学相机和激光测距仪的工作频率对规避策略的影响.设计3 组对比工况,工作频率f分别取(1)f=1 Hz; (2)f=10 Hz; (3)f=0.1 Hz.其余参数设置与3.2.1 节相同.仿真结果如图4 所示.

图4 工作频率敏感性分析Fig.4 Frequency sensitivity analysis

由图4 可知,工作频率降低同样导致滤波精度下降,仿真后期f=0.1 Hz 对应的曲线与其余两种工况有一定误差,但是逃逸器规避机动的效果并无明显区别,即说明规避策略对观测设备的工作频率不敏感.

3.2.4 初始状态敏感性分析

分析追踪器相对于逃逸器的初始状态对规避策略的影响.设追踪器的轨道低于逃逸器120 km,追踪器位于逃逸器后方,相位相差∆ϕ,其余轨道根数相同.设计四组对比工况,相位差∆ϕ 分别取(1) ∆ϕ=0.1◦,(2)∆ϕ=0.2◦,(3)∆ϕ=0.3◦,(4)∆ϕ=0.4◦,其余参数设置与3.2.1 节相同.仿真结果如图5 所示.

图5 初始状态敏感性分析Fig.5 Sensitivity analysis of initial state

相位差∆ϕ 越大,意味着逃逸器越早收到预警信息开始机动.由图5 可知,逃逸器收到预警信息越早,发生脱靶时,追踪器相对于逃逸器的距离越远,即逃逸器的安全性越高,规避效果越好.

3.2.5 逃逸器机动能力敏感性分析

分析逃逸器机动能力对规避策略的影响.设追踪器的最大推力加速度为aNc=1.0 m/s2,逃逸器的最大推力加速度为aNt=kt×aNc,其余参数设置与3.2.1 节相同.针对不同的系数kt设计5 组对比工况,分别为(1)kt=10%,(2)kt=30%,(3)kt=50%,(4)kt=60%,(5)kt=80%.仿真结果如图6 所示.

图6 逃逸器机动能力敏感性分析Fig.6 Sensitivity analysis of escaper maneuverability

由图6 可知,随着kt变大,逃逸器机动能力逐渐增强,当kt=50%,逃逸器不能逃脱追踪器的跟踪,当kt=60%,逃逸器可有效规避追踪器的异常接近.因此可取门限值kt=60%,即逃逸器的机动能力达到追踪器的60%以上时,逃逸器的最大化视线偏转率的规避策略有效.

设置不同的工况验证60% 的门限值是否有效.针对∆ϕ=0.1◦,∆ϕ=0.2◦,∆ϕ=0.3◦,∆ϕ=0.4◦四种情况分别设计(1)kt=50%,(2)kt=60%两组对比工况,仿真结果如图7 所示.

图7 不同初始状态对kt 的影响Fig.7 The influence of different initial states on kt

由图7 可知,针对不同的相位差∆ϕ,逃逸器的机动能力达到追踪器的60%时,逃逸器可有效规避追踪器的异常接近,即60%的门限值有效.

针对追踪器不同的机动能力aNc设计3 组对比工况,逃逸器机动能力为aNt=60% ×aNc,追踪器机动能力取(1)aNc=0.5 m/s2,(2)aNc=1 m/s2,(3)aNc=2 m/s2.

仿真结果如图8 所示.分析可知,针对追踪器不同的机动能力aNc,逃逸器的机动能力达到追踪器的60% 以上时,逃逸器可有效规避追踪器的异常接近,即60%的门限值有效.

综上分析,对于提出的最大化视线偏转率的主动规避策略,可以设置门限值为60%,即逃逸器的机动能力达到追踪器的60%以上时,规避策略有效.

4 结论

图8 追踪器机动能力对kt 的影响Fig.8 The influence of chaser’s maneuverability on kt

本文在航天器近距离追逃博弈的背景下,对逃逸器的主动规避策略进行了研究.建立了基于当前统计模型的机动目标滤波算法,基于比例导引律抑制视线偏转率的基本原理,从最大化视线偏转率的角度入手得到了逃逸器的规避加速度,降低了追踪器比例导引制导率的有效性.通过仿真分析可得出以下结论:设追踪器通过比例导引率异常接近逃逸器,安全距离为100 m,则逃逸器的机动能力达到追踪器的60%以上时,逃逸器采用基于最大化视线偏转率的规避策略进行机动可有效规避追踪器的异常接近;规避策略对观测设备的测量精度和工作频率不敏感;逃逸器收到预警信息越早,规避效果越好.提出的规避策略意义明确、形式解析、易于工程实现.