RM 不稳定过程中预混火焰界面演化及混合区增长预测1)

汪洋 董刚

(南京理工大学瞬态物理重点实验室,南京 210094)

引言

Richtmyer-Meshkov(RM)不稳定是指不同密度且互不浸润的介质间所形成的有一定曲率的界面,在脉冲加速(impulsive acceleration)作用下,其两侧介质发生混合并导致其混合区(mixing zone,MZ)增长的行为,其中脉冲加速通常可由激波冲击来实现.RM不稳定的机制来自斜压效应(baroclinic effect),即,当激波与密度界面作用时,界面形成的密度梯度与激波形成的压力梯度的方向不一致会导致界面上的涡量沉积,在涡量的诱导下界面上的混合区逐渐增长,后期这种增长还会逐渐发展为湍流混合.当界面本身具有化学反应活性时(如预混火焰界面),化学反应会进一步增加RM 不稳定的复杂性.作为一种重要而又复杂的力学现象,带化学反应的RM 不稳定频繁地出现在自然现象(如宇宙超新星爆炸[1])和人类生产生活(如航空发动机超燃混合[2]、惯性约束聚变[3]、工业爆炸灾害[4]等)中.因此,开展带化学反应的RM 不稳定过程的研究,对认识、控制和利用这一现象具有非常重要的现实意义.

对惰性界面条件下的RM 不稳定过程,国内外已经开展了大量的理论、实验和数值模拟研究.界面混合区增长的理论预测模型包含了早期的线性模型[5]以及随后针对激波单次作用下界面RM 不稳定非线性发展过程的渐进模型[6]和势流模型[7-8]等,基于实验结果的适于激波多次作用下的界面混合区增长模型也得到了进一步研究[9-11].文献[12-13]对这些预测模型进行了很好的总结.此外,有学者也采用实验测试的方法针对不同入射激波强度和形状[14-17]、不同初始界面形态[18-21]条件下,RM 不稳定过程的发展进行了细致的研究.数值模拟方面,蒋华等[22-23]采用高精度数值模拟的方法研究了界面初始形态对混合区早期发展过程的影响,并采用理论模型对混合区的增长进行了预测[23];Schilling 等[24]采用类似的数值格式模拟了激波及其反射激波作用下的单模形态界面RM 不稳定过程; Thornber 等[25]采用三维数值模拟,考察了不同初始波长下的界面混合区的增长行为; Lombardini 等[26]利用三维大涡模拟方法研究了单次激波作用下,激波强度对界面混合区发展后期的影响,重点考察了后期界面混合发展特性;Tritschler 等[27]采用两种不同的大涡模拟方法研究了激波及其反射波作用下界面混合区的发展,对界面发展后期小尺度湍流混合特性进行了详尽的分析.

尽管激波与惰性界面相互作用的研究得到了广泛深入地开展,但反应性界面在激波诱导下的发展过程的研究却远远不够.由于特定形态的反应性界面在实验控制上比较困难,因此实验研究几乎未见报道,相关文献仅限于少量的数值模拟研究.Khokhlov等[28]采用二维带化学反应的Navier-Stokes (NS) 方程,数值模拟了单次激波与单模态预混火焰界面的相互作用过程,指出RM 不稳定可促进燃烧放热率,并增加火焰的面积;Kilchyk 等[29]采用带单步化学反应的二维NS 方程,研究了单次激波或膨胀波与单模预混火焰界面相互作用的过程,指出激波压缩效应和火焰长度对反应性RM 不稳定有显著影响.Massa和Jha[30]采用推导得到的二维线化扰动方程,研究了单次激波作用下预混火焰界面的RM 不稳定过程,指出化学反应诱导的压力梯度所形成的斜压效应可以减少火焰表面的小尺度结构、减弱火焰界面的增长,因而很可能会弱化激波驱动的小尺度混合过程.Dong 等采用带单步化学反应的NS 方程对激波及其反射激波与预混火焰界面的多次作用的二维[31-32]和三维[33]过程开展了系列研究,研究了大尺度流动、化学反应以及小尺度扩散等几个因素对反应性RM 不稳定过程的影响,发现化学反应在一定程度上可以削弱大尺度流动带来的界面混合效应,从而证实了文献[30]的推测.此外,Attal 和Ramaprabhu[34]还报道了非预混单模火焰界面的RM 不稳定过程,考察了反射激波对界面的影响,其结果亦表明激波的多次作用明显增加了燃烧效率,该工作同时也反映了反应性RM不稳定研究开始向多样性发展.

上述研究表明,化学反应的存在进一步增加了RM 不稳定现象的复杂性.虽然目前已有众多的理论模型可以预测激波诱导下惰性界面的混合区增长过程,但对于反应性界面的混合区在激波诱导下的增长规律目前并不明确,例如,文献[31-33]主要关注的是RM 不稳定过程中流动和化学反应的时间尺度的变化规律及其对RM 不稳定的影响,而化学反应作用下混合区增长的定量预测并未得到研究,也未见其它文献报道.为此,本文采用高精度数值模拟的方法,研究平面入射激波及其反射激波与正弦形状的预混火焰界面的相互作用过程,重点考察不同化学反应活性条件下界面混合区的发展过程,对化学反应条件下的界面混合区增长速率进行预测,以期为反应性RM 不稳定的混合区发展模型的建立提供参考.

1 数值方法

1.1 控制方程及其计算方法

控制方程采用二维带单步化学反应的Navier-Stokes(NS)方程,表达如下

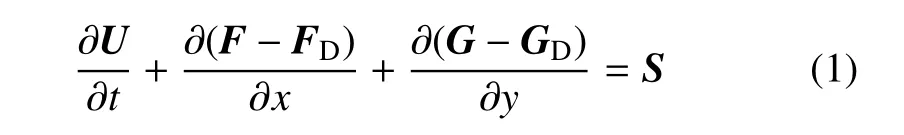
其中

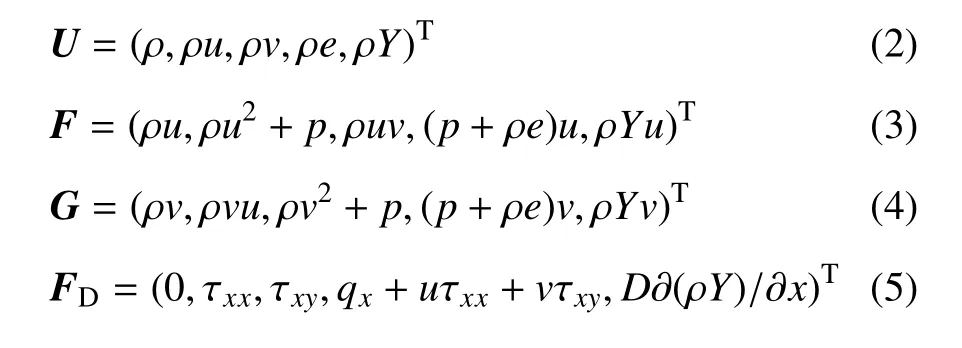
以上各式中,t代表时间,x和y代表空间坐标长度,ρ代表体系的密度,u和v分别为x和y方向的速度分量,Y代表反应物的质量分数,p为体系压力,e是单位质量的总能,表达为

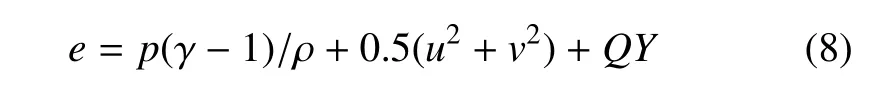
式(8)中,γ 为绝热指数,Q代表单位质量的化学反应放热.qx和qy分别代表x和y方向的热流量,表达为qx=−k∂T/∂x和qy=−k∂T/∂x,T是温度.τij(i=x,y;j=x,y)为黏性应力张量分量,表达为

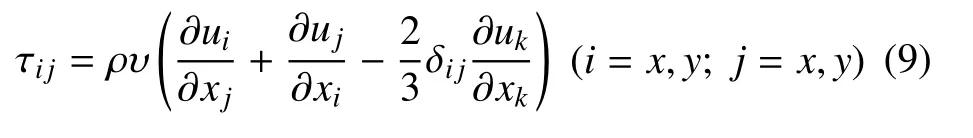
其中,δi j为Kronecker 函数.以上各式中出现的输运系数,如导热系数k,扩散系数D和运动学黏度υ 可统一表达为[4]

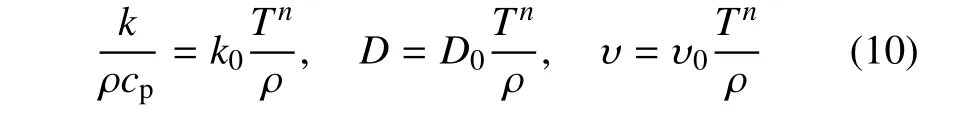
本文计算使用的预混气体参照了文献[35] 中采用的C2H4+3O2+4N2气体,同时假定该预混气的Lewis数、Prandtl 数和Schemidt 数均为1,则式(10)中的k0,D0和υ0为相同的常数,根据文献[4],这些输运系数取值为k0=D0=υ0=3.2×10−7kg/(s·m·K0.7),n取值为0.7.这些取值能够保证输运系数随温度的变化关系很好地符合实际C2H4+3O2+4N2气体的这种变化.

本文采用了基于Arrhenius 形式的单步化学反应描述燃烧现象,因此式(7) 中的反应速率˙ω 可以表达为

式中β 代表指前因子,Ea为活化能,R代表通用气体常数.

对控制方程(1)采用了分裂算法进行求解,其中对流通量的空间导数项∂F/∂x和∂G/∂y采用的是LF(Lax-Friedrichs)格式结合9 阶WENO(weighted essentially non-oscillatory)模板的方法求解[36];输运通量的空间导数项∂FD/∂x和∂GD/∂y采用了10 阶中心差分的格式进行求解; 而化学反应源项S和解U的时间导数项∂U/∂t则采用了3 阶Runge-Kutta 方法进行求解.上述控制方程及其计算方法在以前的研究中已经得到了广泛应用[31-33].

1.2 计算条件与验证

本文模拟的激波与预混火焰界面相互作用的计算构型如图1(a) 所示,计算域为二维矩形形状.初始时刻,平面入射激波(incident shock wave,ISW) 位于计算域距下边界为l1的位置并开始向上运动,在运动过程中与波长为λ,初始振幅为a0的正弦形预混火焰界面(flame interface,FI)发生相互作用.令火焰界面的下方为密度较大的未燃预混气(绿色部分),火焰上方为密度较小的等压燃烧条件下的已燃气体(蓝色部分),则激波从大密度侧向小密度侧越过火焰界面后会形成继续上行的激波和向下反射的稀疏波.上行激波行至计算域顶端的刚性壁面后会反射下行,下行激波则再次和火焰界面发生相互作用,作用后的激波会继续反射向顶端壁面方向运动,经过再次反射后又会下行与界面发生作用.这个过程会一直进行下去,直至反射激波强度逐渐减小至激波不再明显为止.

图1 正弦预混火焰界面的(a)初始形态和(b)典型的发展过程.ISW 为入射激波,FI 为火焰界面Fig.1 (a)Initially sinusoidal pattern and(b)developed pattern of flame interface induced by shock wave.ISW is incident shock wave,FI is flame interface

令初始的正弦形火焰界面数学形式如下

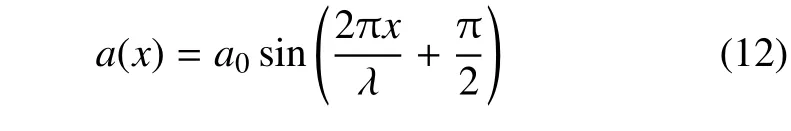
这里a(x)代表正弦火焰界面的流向(y方向)振幅沿x方向的变化.从界面的角度看,在入射激波的作用下,火焰界面经RM 不稳定过程发生变化,典型的形态如图1(b)所示.可以看到,二维正弦形界面在激波的单次作用下演变为“钉(spike)−泡(bubble)”结构,其中钉结构比较复杂,它还包含了其上的“帽(cap)”结构和两侧的“涡(vortex)” 结构.定义“帽” 的顶部到“泡” 的底部的流向长度为界面混合区宽度WMZ,则该量是评价界面RM 不稳定发展过程的重要物理量[12,24].

本文计算中,选取计算域流向长度为l1+l2=0.6 m,其中l1=0.1 m 以保证整个计算过程中入射激波与界面作用后形成的下行稀疏波不会走出下边界而影响边界条件; 计算域的横向长度为正弦界面波长λ=0.012 8 m.计算域的左右边界为周期性边界条件,上边界为绝热刚性无滑移的壁面条件,下边界为零梯度边界条件.假设本文气体符合量热完全气体的假设,并令初始时刻波前未燃气体(图1(a)中绿色区域)的初始温度和初始压力分别为T0和p0,则波后未燃气(图1(a)中红色区域)的状态可由激波关系式求出.本文界面初始形态参数、预混气的热力学和动力学参数的取值[33]均列入表1.

表1 计算参数[33]Table 1 Computational parameters[33]

此外,在本文计算中设初始平面入射激波Mach数为M0,则根据一维激波与界面相互作用的数值模拟,可以确定入射激波作用后的界面Atwood 数A=(ρ1−ρ2)/(ρ1+ρ2) (这里ρ1和ρ2分别代表界面两侧重和轻介质的密度)和界面两侧流向速度差∆V,以及第一次反射激波作用后的界面Atwood 数A1和界面两侧的流向速度差∆V1,这些与一维流动有关的参数值也列入表1.

为研究不同预混气的化学活性对RM 不稳定发展的影响,用不同活化能的数值来表征不同的化学反应活性,活化能的变化的范围列入表1 中,此外,还计算了化学冻结流条件下的预混火焰界面的发展过程.化学冻结流是一种保留了预混火焰热力学状态但将化学动力学过程进行冻结(设Ea无穷大,即反应速率为零)的理想状态,考虑的目的是为了通过与反应流计算结果的对比来分析活化能的影响.在本文计算中,计算了7 种不同活化能(Ea/RT0=30.0,31.2,31.6,32.0,32.5,38.2,50.0)的反应流以及冻结流(Ea/RT0=∞)的界面混合区发展过程.但在后面的分析中,主要是以Ea/RT0=30.0,38.2,50.0 和冻结流等4 种典型条件的结果为主,其中活化能Ea/RT0=38.2的算例为基准算例,其活化能取值来自文献[37].

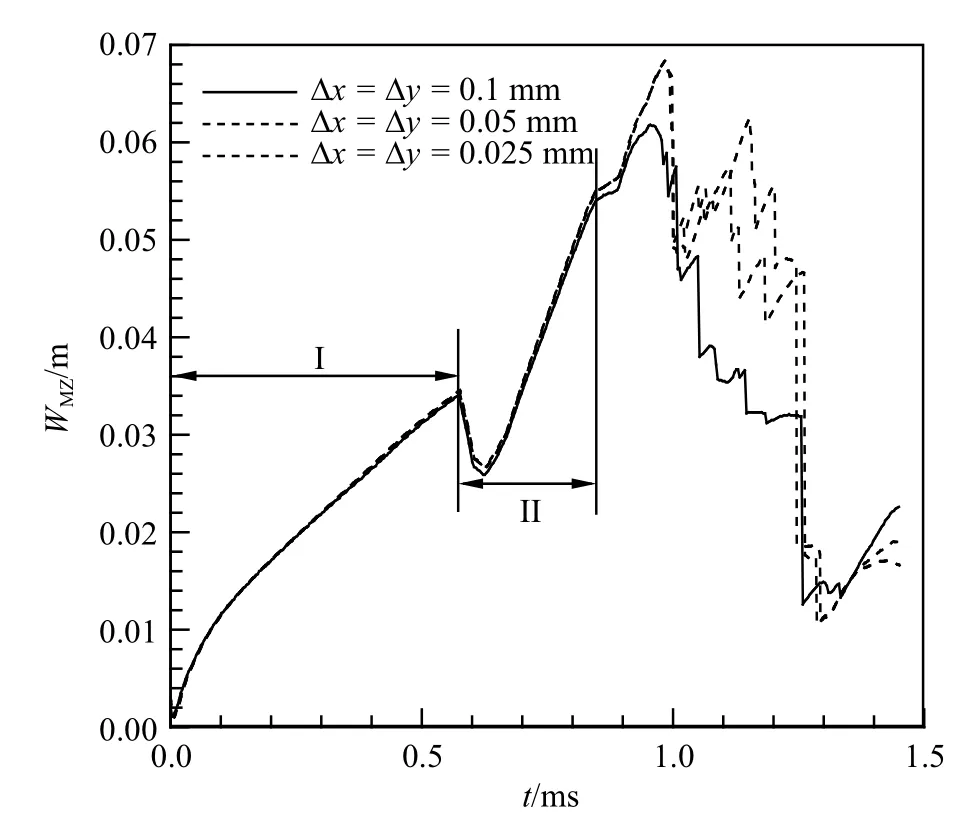
图2 不同网格尺寸下计算的混合区宽度随时间的变化Fig.2 Time histories of width of mixing zone with different grid resolutions

为考察本文计算结果的有效性,首先针对Ea=38.2RT0条件下的激波与预混火焰相互作用过程的数值模拟进行了网格无关性验证.本文采用了均匀正交的正方形网格来划分计算区域,选取了三种不同的网格尺寸(∆x=∆y=0.1 mm,0.05 mm 和0.025 mm)进行激波与正弦形预混火焰界面相互作用过程的数值模拟.图2 给出了3 种网格尺寸下计算得到的火焰界面发展过程中混合区宽度(WMZ,定义见图1(b))随时间的变化过程.图中时间范围I,II 分别为入射激波和第一次反射激波作用后WMZ的变化阶段,可以发现阶段II 的初期存在一个短暂的WMZ下降的过程,这是由于反射激波掠过火焰界面时对界面的压缩所导致的.图中结果表明,在阶段I 和II 中,3 种网格尺寸计算的结果均相互吻合较好,但在阶段II 之后的后继反射激波与火焰界面的作用过程中,∆x=∆y=0.1 mm 尺寸下计算的结果要明显低于∆x=∆y=0.05 mm 和0.025 mm 两种尺寸下计算的结果,尽管后两者的计算结果之间也略有差别.阶段II 后计算结果的差异不仅体现了计算网格尺寸的影响,实际上也表明火焰界面的失稳向着小尺度结构甚至是湍流混合的方向发展,这超出了本文采用的控制方程和网格尺寸所研究的范围,因此,本文研究仅考虑阶段I 和II 的相互作用过程.根据网格无关性测试的结果,本文采用∆x=∆y=0.05 mm 的网格尺寸对所有算例开展数值模拟,每一个算例总网格数均为307.2 万个,为提高计算效率采用了基于MPI的并行策略编制程序开展计算.

2 结果与讨论

2.1 阶段I 的界面演化

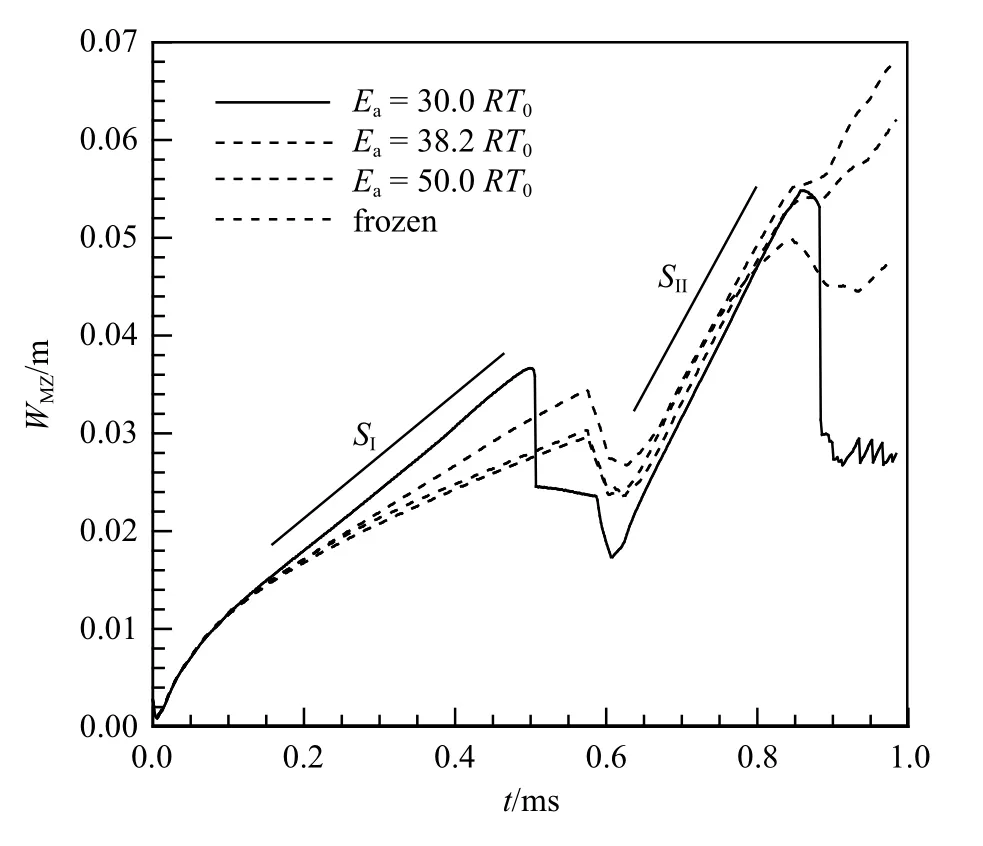
图3 不同化学活性下混合区宽度随时间的变化. SI 为入射激波作用阶段混合区增长速率,SII 为反射激波作用阶段混合区增长速率Fig.3 Time histories of width of mixing zone with different chemical activities. SI is growth rate of mixing zone at incident shock wave stage,SII is growth rate of mixing zone at reflected shock wave stage

图3 首先给出了3 个典型活化能(Ea=30.0RT0,38.2RT0和50.0RT0) 的反应流以及冻结流下反应区宽度(WMZ) 随时间的变化.可以看到,阶段I 中四个算例在经历了短暂的相同的发展过程(t< 0.1 ms)之后,其WMZ的增长快慢开始不同,活化能最小(Ea=30.0RT0)的算例增长最快,而活化能最大(Ea=50.0RT0) 以及冻结流的算例增长最慢.进一步观察可以发现,阶段I 的发展过程中尽管不同化学反应活性下的界面混合区增长快慢不同,但均呈现线性增长的形式,通过对计算结果的线性拟合可以确定其WMZ的增长速率SI.

在进一步定量研究SI之前,首先考察了火焰界面在阶段I 的演化规律和混合区宽度的增长行为.图4 显示了阶段I 中4 个典型时刻(t=0.2,0.3,0.4 和0.5 ms)下,用反应物质量分数(Y)标记的界面形态的变化,每个时刻下的4 个子图从左到右分别代表了活化能为Ea=30.0RT0,38.2RT0和50.0RT0的反应流以及冻结流等4 种不同反应活性的情况.在t=0.2 ms时(图4(a)),4 种条件下的界面结构均呈现出“钉−泡” 结构,钉结构的上方和两侧也分别呈现出“帽”结构和涡结构(见图1(b)的说明).但是,当反应活性强(Ea=30.0RT0)时,涡结构内反应物几乎完全消耗,这说明化学反应的作用首先是发生在涡结构中的,其原因主要是因为RM 不稳定过程中形成的涡结构使得界面两侧的未燃气与已燃气进行了充分的掺混,这种强化的传热和传质过程进一步促进了化学反应的进行.该时刻下的结果还表明,不同反应活性下混合区宽度的变化差异不大.当t=0.3 ms 时(图4(b)),可以发现随着反应活性的增强,涡结构内的混合过程逐渐被化学反应过程所替代,其中,Ea=30.0RT0条件下的反应流其涡结构不再明显,界面上方形态主要以“钉−帽” 结构为主并明显向上移动,从而导致其混合区宽度也较其他几种情况更长.当t=0.4 ms时(图4(c)),除了界面上方的“钉−帽−涡” 结构继续发展外,还可以看到界面下方的泡结构随着反应活性的增强也逐渐向下移动,活性越强,“泡”结构向下发展越快,因此导致整个混合区宽度随着活性的增强而逐渐变大,进而导致图3 中阶段I 的WMZ变化规律.到t=0.5 ms 时(图4(d)),可以看到,反应活性最强(Ea=30.0RT0) 的算例,其“帽” 结构已经由化学反应所消耗,因而只留下钉结构,这也导致其反应区宽度出现了突然的下降(见图3);而活性次强(Ea=38.2RT0)的算例,其涡结构不再明显,但形成的“钉−帽”结构开始使界面混合区明显向上发展,这与Ea=30.0RT0的算例在t=0.3 ms 时的结构类似.此外,随着反应活性的增强,界面下方的泡结构也进一步向下发展.

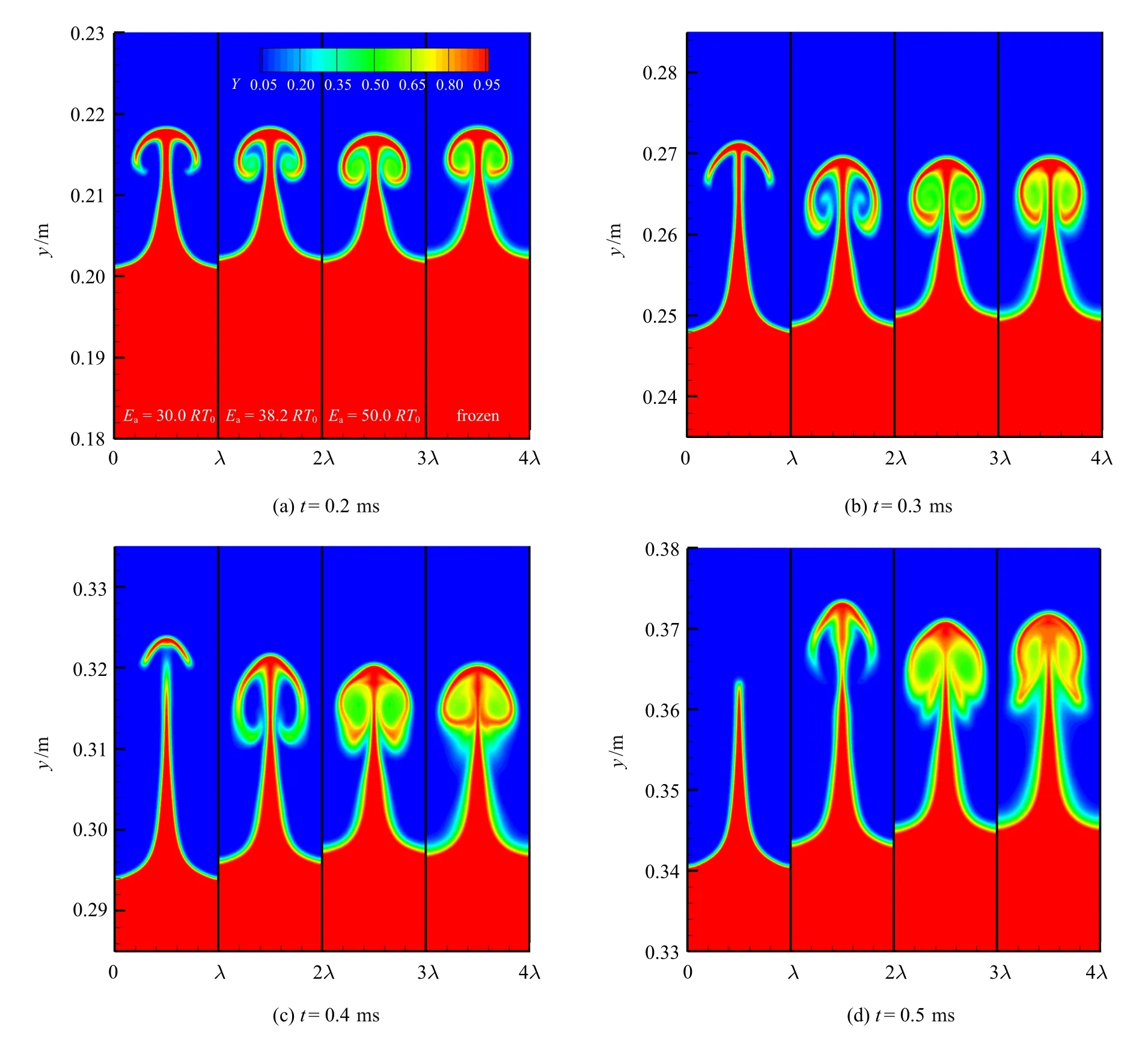
图4 阶段I 中不同时刻的界面形态Fig.4 Patterns of flame interface at the different instants for stage I

根据以上的界面形态的演化过程,可以发现,阶段I 中混合区宽度随时间的变化是由“钉−帽”结构向上发展以及泡结构向下发展所共同决定的.化学反应活性对这一过程的影响十分显著,化学反应越强(活化能越小),“钉−帽”向上发展以及“泡”向下发展越显著,因此使得反应区宽度越大.

2.2 阶段I 混合区宽度预测

2.1 节首先观察了不同反应活性条件下界面形态及界面混合区宽度随时间的演化规律,发现化学反应对界面上方的“钉−帽”结构以及下方的“泡”结构均有显著影响.为发展定量预测阶段I 的混合区增长速率SI的模型,图5 进一步考察了t=0.4 ms 时的界面结构及流场特征.图5(a) 将四种反应活性条件下界面轮廓(用Y=0.9 的等值线表示)进行了叠加对比,可以发现,界面下方“泡”结构下缘随着反应活性的增加不断下移,这种下移符合预混火焰传播的特征:反应活性越大,化学反应速率越大,则火焰传播速度也越大.因此可以得出结论:反应性预混火焰界面混合区宽度的增长其部分原因是由预混火焰传播所贡献的.根据经典的Frank-Kamenetsky 层流火焰传播理论[38],层流预混火焰的传播速度可以表达为

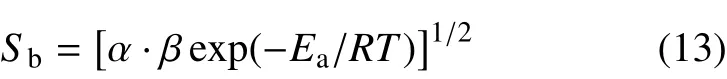
式中,Sb为“泡” 结构的向下发展速度,也代表了层流预混火焰的传播速度; α 为热输运系数,α=k0Tn,n=0.7;k0,β,Ea和R的含义及取值见表1;T代表入射波后的已燃区温度,本文取T=7.0T0.

此外,观察界面上方“钉−帽” 结构,可以看出,反应活性越强,则“帽” 结构的上缘越向上移,但其结构较为复杂,并不符合预混火焰的传播规律.为此,图5(b) 进一步给出了界面附近的涡量幅值|ω|=|−0.5(∂u/∂y−∂v′/∂x)|以及速度矢量V=(u,v′)的分布,这里v′=v−vp,vp为入射激波波后流场的平均速度.首先观察涡量幅值分布可以看出,随着反应活性的增强,流场的涡量明显减弱,这说明化学反应的加入可以抑制涡量的形成,这与之前研究得到的结论相一致[30].接下来观察速度矢量的分布可以看到,当化学反应较强(如Ea=30.0RT0) 时,钉结构两侧的涡量变弱,漩涡结构不明显,因此对入射激波波后流动速度抑制不够明显,因此“钉−帽” 结构上方的流体流向速度较大.反之,当化学反应较弱(如Ea=50.0RT0) 或化学反应冻结时,由于钉两侧存在较强的互为反向的涡旋,涡旋外侧诱导的向下的运动速度实际上抵消了波后流体向上的运动.

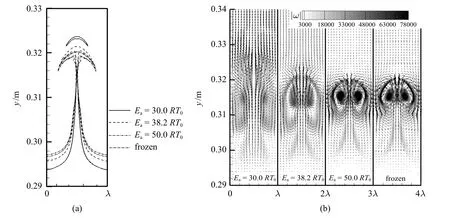
图5 t=0.4 ms 时不同化学活性条件下(a)反应物质量分数Y=0.9 的等值线对比,(b)流场涡量幅度和速度矢量分布对比Fig.5 (a)Comparisons of(a)mass fraction contours with Y=0.9 and of(b)vorticity amplitude and velocity vector among cases with different chemical activities at t=0.4 ms

为验证上述分析,图6 给出了计算域中心(x=λ/2) 处由于涡的旋转所诱导的界面两侧的速度差∆Va(本文称诱导速度)沿流向的分布,该速度差由界面上、下侧中心处流向速度的差值所确定.图6 的结果表明,虽然在较弱活性(Ea=50.0RT0)或冻结流的条件下,较强的漩涡对在其之间(y=0.031 6 m 左右)的流体所诱导的流向速度差较大,但在“钉−帽” 结构的上方(y>0.032 5 m)其速度差迅速变小至反向流动,说明漩涡外侧的向下流动对速度差的减小起着很大作用.相反,对活性较强的反应流(Ea=30.0RT0),由于漩涡强度弱,漩涡外侧诱导的反向流动速度较小,因此涡对之间形成的正向速度差可以一直维持.通过以上分析可知,界面“钉−帽” 结构受化学反应的影响比较复杂,但是较强的反应活性导致了其上方的具有较大的诱导速度差,进而使得“钉−帽” 结构向上发展得更快,由此可将其向上的发展速度表达为

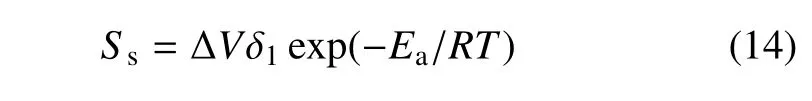
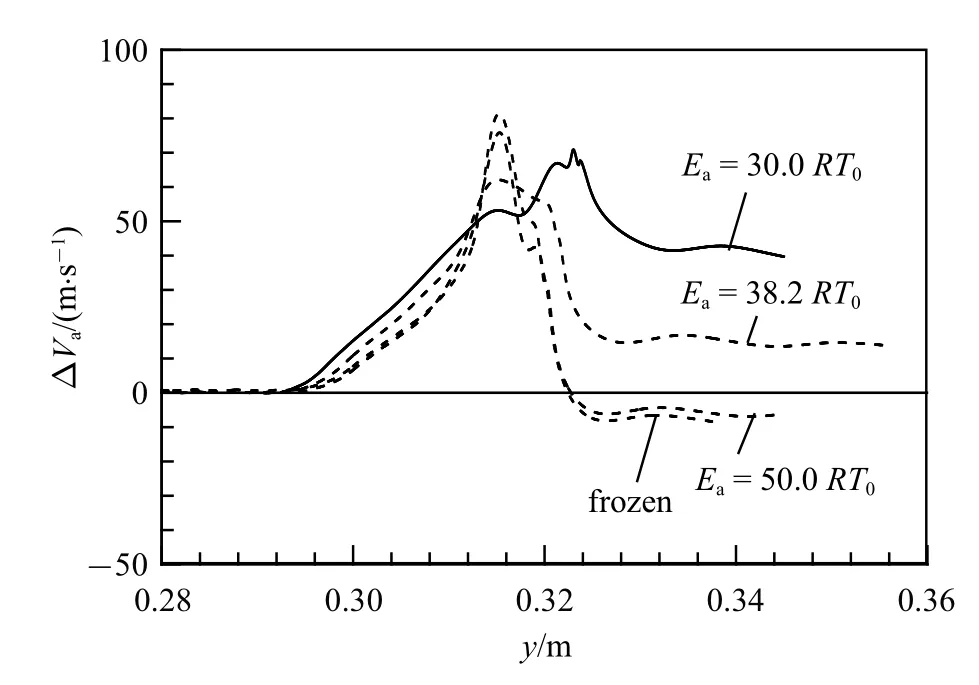
图6 t=0.4 ms 时不同化学活性条件下轴线上流向诱导速度分布Fig.6 Distributions of streamwise induced velocity at centerline for cases with different chemical activities at t=0.4 ms

式中∆V代表一维构型下入射激波波后的界面两侧流向速度差,其值参见表1,δ1为阶段I 的经验常数.式(14)等号右端exp(−Ea/RT)反映了化学反应活性对界面上缘“钉−帽” 结构发展的影响,反应活性越强,该项越大,则Ss越大,因此符合图5(b)和图6 的分析.

本文假设所考虑的流场具有层流流动特性,因此化学反应和湍流的相互作用可以忽略,故综合上述分析,可以采用线性叠加的方式给出阶段I 中火焰界面的混合区宽度增长速率SI的表达式

式中,SRM代表RM 不稳定导致的混合区宽度增长速率,Sc代表化学反应导致的混合区宽度增长速率.前者可以采用传统的各类基于RM 不稳定的理论模型进行预测[12-13],后者由于层流流动的假设仍可采用如下线性叠加的方法进行求解

式中Sb和Ss分别由式(13)和式(14)进行求解,其中涉及到的变量仅为活化能Ea,表明了化学反应活性的影响,而其余各常量均可由初始条件和一维激波界面作用得到的参数来确定.

注意到式(14)中δ1为经验参数,为确定该值,本文对图3 数值模拟得到的结果进行线性拟合可以得到SI,令冻结流的SI=SRM(即冻结流的WMZ增长速率不考虑化学反应,仅由RM 不稳定所导致),则由式(15)可以求得数值模拟条件下的不同Ea的Sc值.图7 给出了采用数值模拟得到的Sc随Ea的变化关系,可以看出,随着活化能的减小,Sc呈指数增大.进一步采用式(13)、式(14)和式(16)进行计算,发现当δ1=9.3 时,利用式(16)预测模型得到的Sc与数值模拟得到的Sc吻合良好.图7 中还给出预测模型中Sb和Ss随活化能的变化,可以发现,随着活化能的减小,火焰界面上方“钉−帽” 结构的增长速度比界面下方“泡”的增长速度要更快.

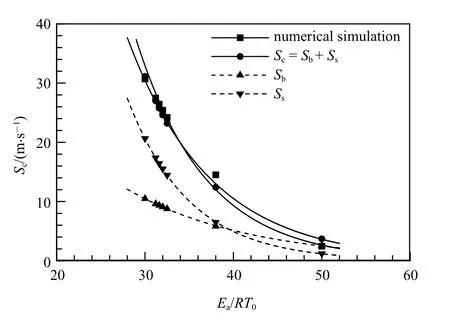
图7 数值模拟与理论预测的Sc 的比较Fig.7 Comparisons of Sc between numerical and predicted results

2.3 阶段II 界面演化及混合区宽度分析

观察图3 中阶段II(即第一次反射激波作用后的火焰界面发展阶段)可以看出,反射激波作用后,不同化学反应活性的反应流和冻结流条件下,界面混合区宽度的增长速率(用SII表示)趋于一致,其增长速率也明显大于阶段I 的增长速率.为了解WMZ的增长规律,图8 显示了阶段II 的两个典型时刻(t=0.7 ms和0.8 ms)下,不同化学反应活性下界面的发展形态.图8(a)的结果(t=0.7 ms)表明,反射激波与火焰界面作用后,混合区宽度仍然沿流向持续增长,当反应活性较强时,界面呈现出沿流向的细长结构,随着反应活性的下降,界面形状逐渐变得复杂,已燃气和未燃气相互掺混形成的二维混合区变得越来越明显.然而从混合区宽度的变化来看,不同活性下的混合区宽度变化并不明显,即,随着反应活性的增强,界面上方的“钉−帽”结构和下方的“泡结构”均同时下移,表明此时界面上下存在同样的预混火焰传播过程,两者传播方向相同,因此对界面上、下方发展的影响相互抵消,从而导致混合区宽度对反应活性的依赖不再变得明显.图8(b)的结果(t=0.8 ms)也显示了类似的规律.需要注意的是冻结流条件下,界面形态开始失去对称性,这表明到第一次反射激波后期界面的小尺度流动开始增加,界面逐渐向湍流混合的阶段发展,因此,本文的研究仅限于第一次反射激波作用后的阶段II.后继的二次及多次激波与火焰界面的相互作用不在本文研究的范畴.

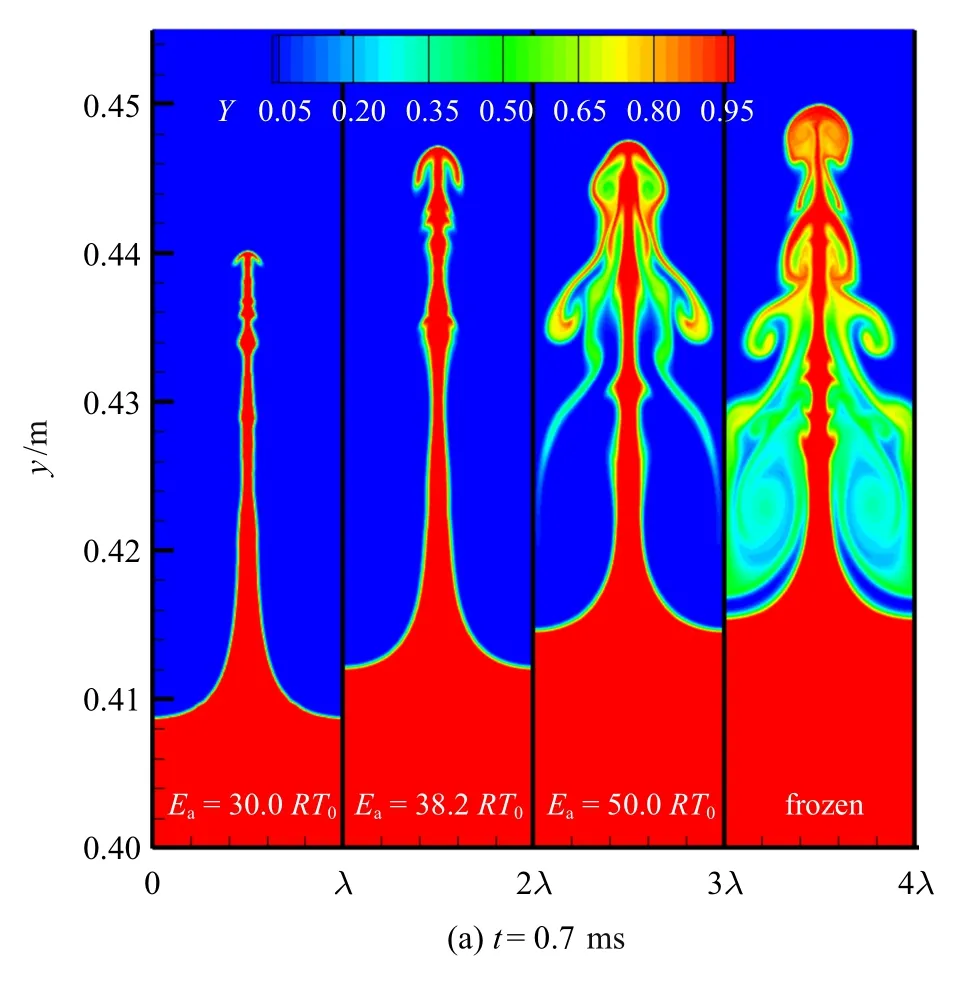
图8 阶段II 中不同时刻的界面形态Fig.8 Patterns of flame interface at the different instants for stage II

图9 进一步给出阶段II 中t=0.7 ms 时,不同反应活性条件下中心线上流向诱导速度∆Va沿流向的分布.由结果也可以看出界面下方反射激波作用之后的区域(y=0.39 ∼0.41 m) 和界面上方的区域(y> 0.45 m)诱导速度均趋于零,这说明入射激波和反射激波对火焰界面附近的涡旋运动的影响相互抵消,因而界面混合区的发展不再考虑涡旋运动对化学反应的影响,这一点与阶段I 中界面混合区的发展有所不同.

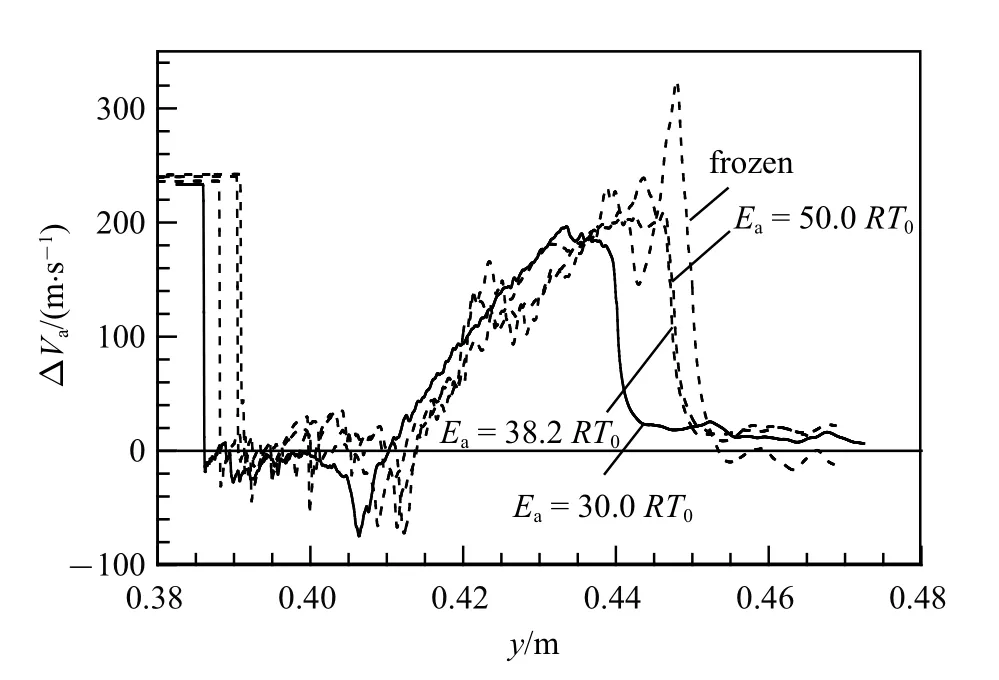
图9 t=0.7 ms 时不同化学活性条件下中心线上流向诱导速度分布Fig.9 Distributions of streamwise induced velocity at centerline for cases with different chemical activities at t=0.7 ms

采用与式(15)相同的形式表达阶段II 的混合区增长速率SII

式中变量符号与式(15)相同,下标II 代表阶段II.根据前面分析,由于涡旋运动不再对火焰界面产生额外影响,界面下方“泡”结构和上方的“钉−帽”结构仅存在相似的火焰向下传播的过程,因此导致两者作用相互抵消,即Sc,II=0.因此,混合区宽度的变化仅由惰性RM 不稳定过程所决定,采用反射波后的Mikaelian 模型[8]对其增长速度进行预测,式(17)可表达为

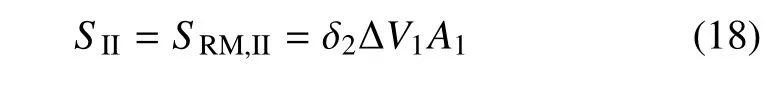
式中δ2为阶段II 的经验常数,∆V1和A1的取值见表1.由7 种不同活化能条件下的反应流以及冻结流的数值模拟结果可以拟合得到不同的SII值,由此得到的平均值为149.1 m/s,标准偏差为3.2 m/s,将平均增长速度(149.1 m/s)代入式(17)可以得出δ2=0.79.需要说明的是,原始的Mikaelian 模型[8]中经验常数δ2=0.28,但进一步的研究也表明[12],δ2的数值依赖于界面的形态与结构,比如对惰性界面和密度梯度很大的界面,二维和三维计算采用的δ2分别可取0.55和0.84.本文δ2取0.79 反映了预混火焰界面与原始Mikaelian 模型中不存在温差的界面是有所区别的.

3 结论

采用带单步反应的Navier-Stokes 方程,对入射激波及其反射激波与正弦形状的预混火焰界面相互作用过程进行了二维数值模拟,考察了介质反应活性对界面形态演化和混合区增长过程的影响.得到的主要结论如下:

(1)正弦形预混火焰界面在入射激波作用后沿流向不断拉伸,除常规RM 不稳定诱导的界面混合区增长外,与化学反应相关的预混火焰传播对界面下方的“泡”结构的发展起到了促进作用,而化学反应与涡结构的相互作用减弱了涡的强度,促进了界面上方的流体流向运动进而使“钉−帽”结构沿流向不断发展.化学活性越强,界面的流向增长越快.

(2) 沿流向发展的火焰界面在反射激波的作用下,沿流向继续发展,其中界面下方的“泡” 结构和上方“钉−帽” 结构均受到火焰向下传播的影响,故化学反应的作用抵消,从而导致反射激波作用后界面的发展基本不依赖于介质的化学反应活性.

(3)根据上述界面演化机理,一方面提出了入射激波作用阶段,化学反应导致的界面增长速率Sc的表达式,该表达式仅依赖于介质的反应活化能和初始条件,具有较好的通用性;另一方面指出仍可以采用Mikaelian 的模型预测反射激波作用下火焰界面的混合区增长速率,但模型常数要进行修正.