流向磁场作用下圆柱绕流的直接数值模拟1)
2020-12-23郝乐陈龙倪明玖
郝乐 陈龙 倪明玖
(中国科学院大学,工程科学学院磁流体力学实验室,北京 101408)
引言
在障碍物绕流的研究当中,圆柱绕流是一个简单又经典的模型[1-3],包含了非常复杂的流动形态,如障碍物表面的边界层,障碍物两侧的剪切层,回流区和尾迹区域等.圆柱尾迹区域的流动行为取决于这些边界层的状态,不同雷诺数(Re)下,这些区域可以是层流,转捩或湍流状态.由于圆柱绕流湍流的复杂性,直接数值模拟研究仍存在巨大的挑战.
核聚变托卡马克装置中,包层是能量转换的关键部件,具有实现氚增殖和辐射屏蔽等功能,而液态锂铅增殖剂包层是其中最具发展潜力的概念之一.锂铅流体作为液态包层中主要的流动介质,与磁场相互作用形成磁流体力学(magnetohydrodynamic,MHD)效应.而包层内的流动通道非常复杂,包括了同芯母管及流道插件(FCI) 等结构[20].因此绕流是其中非常重要且常见的流动形式,而感应洛伦兹力则会显著改变这种绕流的流场结构.另外需要注意的是,为了更好的带走热量,包层内液态金属的流速较大,Re高达105,因此流动通常呈湍流状态.
但由于液态金属的非透明性,实验很难测得流动内部真实的三维速度分布.Rhoads 等[21]基于电势探针法对自由界面下Re10 000 的圆柱绕流湍流进行了实验研究,通过电势差得到了流场的速度,并进一步分析了尾迹的速度波动规律和尾迹涡结构的形态演化.但实验测量的区域毕竟有限,而且根本无法观察到液态金属内部的流场结构.因此开展磁场作用下绕流湍流的直接数值模拟研究具有重要意义,它不仅可以拓展参数范围同时能观察到更细致的三维流场结构,使得深入机理性研究成为可能.
强磁场作用下,Potherat 等[22]基于MHD 准二维模型[23],对Re6000 的圆柱绕流进行了模拟.研究表明磁场可以延缓剪切层的分离,同时作者发现了4种典型的流动机制(蠕流、稳定涡对、卡门涡街及壁面涡脱落),并得到了回流区长度、阻力系数、压力系数及斯特劳哈尔数(S t)与(Re,Ha)组合的关系.采用同样的方法,Hussam 模拟了圆柱位于对称线上[24]以及圆柱靠近壁面情况下[25]的流动传热问题,获得了阻力系数、传热效率等随磁场强度的变换关系.Chatterjee 等[26]则模拟了强磁场下方柱绕流的流动传热问题,获得了类似的结论.但上述模拟的前提条件是,哈特曼数(Ha,表征电磁力与黏性力的比值)以及相互作用数(N,表针电磁力与惯性力的比值)都要远大于1.
Muck 等[20]对弱磁场情况下Re=200,250 的方柱绕流进行了三维直接数值模拟,揭示了涡结构从三维结构向准二维结构转换的物理机制,并发现了在相互作用数很小的情况,阻力系数和压力系数的非单调变化情况.但N1 情况下,尤其是柱体绕流为湍流运动时,国内外并没有相关的三维数值研究,尾迹结构中涡重构的内在机理也尚不清楚,急需开展相关的直接数值模拟工作,以便更好地指导液态包层的设计工作,对于包层的安全高效运行也具有十分重要的学术意义和工程应用价值.
本文首先模拟了无磁场下圆柱绕流Re=3900的算例,并与前人的研究进行对比,结果吻合很好,同时分析了圆柱绕流湍流的统计特性.在此基础上施加流向磁场,探究磁场对圆柱绕流湍流速度场、雷诺应力和回流区长度的影响.
1 算例设置
1.1 模型及控制方程
本文的物理模型如图1 所示,圆柱直径D为特征长度.模型流向总长为L=20D,圆柱中心距离入口截面L1=5D,距离出口长度L2=15D.方形管道横向总长度L=20D,圆柱中心距离上下壁面10D.几何尺寸的确定参考了Tremblay[14]的工作.展向长度设为Lz/D=π,这与多数学者[27-29]的模型设置相一致.Breuer[15]发现计算模型展向方向从πD增长到2πD,保持展向相同的网格分辨率对结果影响不大,这个发现与Kravchenko 和Moin[29]的观点是一致的.此模型尺寸设置既可以保证流场结构的完整性又可以合理节省计算成本.

图1 计算模型示意图Fig.1 Schematic diagram of calculation model
模型中液态金属为不可压导电牛顿流体,运动黏性系数为ν,电导率为σ,密度为ρ.沿流动方向施加一个恒定的外部均匀磁场.圆柱与管道壁面为绝缘无渗透条件.本文的计算中,磁雷诺数Rem=uLµσ ≪1,诱导磁场相对于外加磁场是个无穷小量可以忽略不计.因此,无量纲磁流体动力学控制方程可以写成如下形式
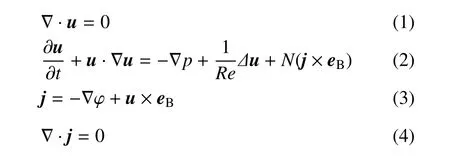
其中变量u,j,P,eB,φ 分别代表速度、电流密度、压力、磁场和电势.特征速度为入口均匀来流速度U0,外加磁场强度B0.方程中两个重要的无量纲参数分别为雷诺数Re=U0D/ν,表征惯性力比黏性力的比值,及相互作用参数N=B2Dσ/(ρU0),表征电磁力与惯性力的比值.而哈特曼数,代表了磁场力与黏性力之比.特别声明本文所有的计算都基于软件平台MHD-UCAS[30]进行.
1.2 边界条件
无磁场工况下入口为均匀无扰动来流,速度为U0.出口采用无反射对流边界,∂u/∂t+U0∂u/∂n=0.展向和横向为周期性边界条件,不考虑壁面对流动的影响.圆柱表面是无滑移边界,因此在圆柱背部两侧表面会产生分离剪切层.当流动达到充分发展状态时,t=300D/U0,沿流动方向施加恒定磁场.为保证壁面绝缘,壁面上电势的边界条件设为纽曼边界∂φ/∂n=0.进出口由于没有电流进入或离开,因此给定电势边界为∂φ/∂n=(u×eB)·n.
模拟过程中时间步长恒定,∆t=0.001D/U0,最大的库朗数(CFL) 不超过0.25,确保计算的稳定性.初始流场为静止流场,最终为一个统计稳定状态.本文采用有限体积法数值模拟,应用投影算法处理了压力与速度的耦合.基于相容守恒格式[31-32]求解电势泊松方程,以保证电荷守恒.计算在空间和时间上都具有二阶精度.相关模拟均在天河二号超级计算机上完成,每个算例均运用了20 个节点(480 个核)进行并行计算.
1.3 网格无关性验证
为保证计算精度,同时节省计算资源,本文设定了3 套网格进行了网格无关性验证,如表1 所示,表中Lr为平均回流区长度,Cd为平均阻力系数.其中Ncyl表示圆柱周向的网格数,∆nwalls表示距离圆柱第一层网格的厚度,Nr表示双“O”型间的径向网格数,Nz表示展向的网格数,Nt表示网格总数.圆柱壁面附近采用双曲正切函数进行网格分布,因此近圆柱壁面网格相对密集,而在垂直固壁方向,网格采用线性增长方式进行分布.远离圆柱的上下游区域网格相对均匀.同时为了使近圆柱区域的网格具有更好的正交性,采用如图2 所示的双O 型网格分布.

表1 网格相关参数设置对时均流动特性的影响Table 1 Effect of grid design on time-averaged flow characteristics
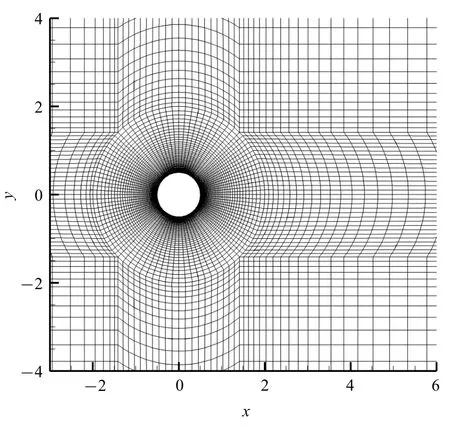
图2 双O 型网格分布Fig.2 The distribution of double curvilinear O-type orthogonal grids
不同网格计算得到的斯特劳哈尔数,平均回流区长度及平均阻力系数如表1 所示.可以发现基于最粗网格G1 与最细网格G3 所得结果的最大误差约为5.39%,若采用较细的两组网格(G2,G3),这一误差将进一步减小,约2.99%,且所得结果与前人的实验结果[5,33]吻合很好,因此网格G3 足够精确地求解当前流动.
对于直接数值模拟而言,湍流区的最小网格尺度必须需达到Kolmogorov 尺度(η) 的量级(O(η)),其中η=(ν3/⟨ε⟩)1/4,⟨ε⟩ 表示局部湍动能的时间平均耗散.Moin 等[34-36]的研究表明,最大网格尺度比(∆x,y/η)1 的要求实际上过于严苛,因为Kolmogorov尺度位于耗散区域的最末端,而对于平板湍流而言,大部分的能量耗散都发生在尺度30η 的结构上.因此,当满足最大网格尺度比(∆x,y/η)10 时,就足以精确计算一阶二阶统计量.而本文采用的G3 网格,最大网格尺度比(∆x,y/η)6.4,位于剪切层区域.
2 无磁场下圆柱绕流湍流验证及分析
2.1 速度场
首先通过与前人的研究结果进行比对,包括实验和模拟,验证程序的准确性.为了得到准确的时均积分量,本文的平均时间为60 个旋涡脱落周期(t=300D/U0),同时所有积分量都进行展向平均处理.
如图3 所示,由于无滑移边界条件的存在,柱体底部的平均流向速度始终为零.流速在回流区达到极小值,然后迅速上升到稳定值.通过与实验的对比,发现模拟结果较好地预测了回流区速度极小值umin和回流长度Lr.从图中可以确定出,无磁场工况下回流区的长度为Lr=1.69,与文献比对在合理的范围内.而且通过下文的分析发现流向磁场会显著改变回流区长度.

图3 圆柱中心线上流向平均速度Fig.3 Mean streamwise velocity along the centreline of the cylinder
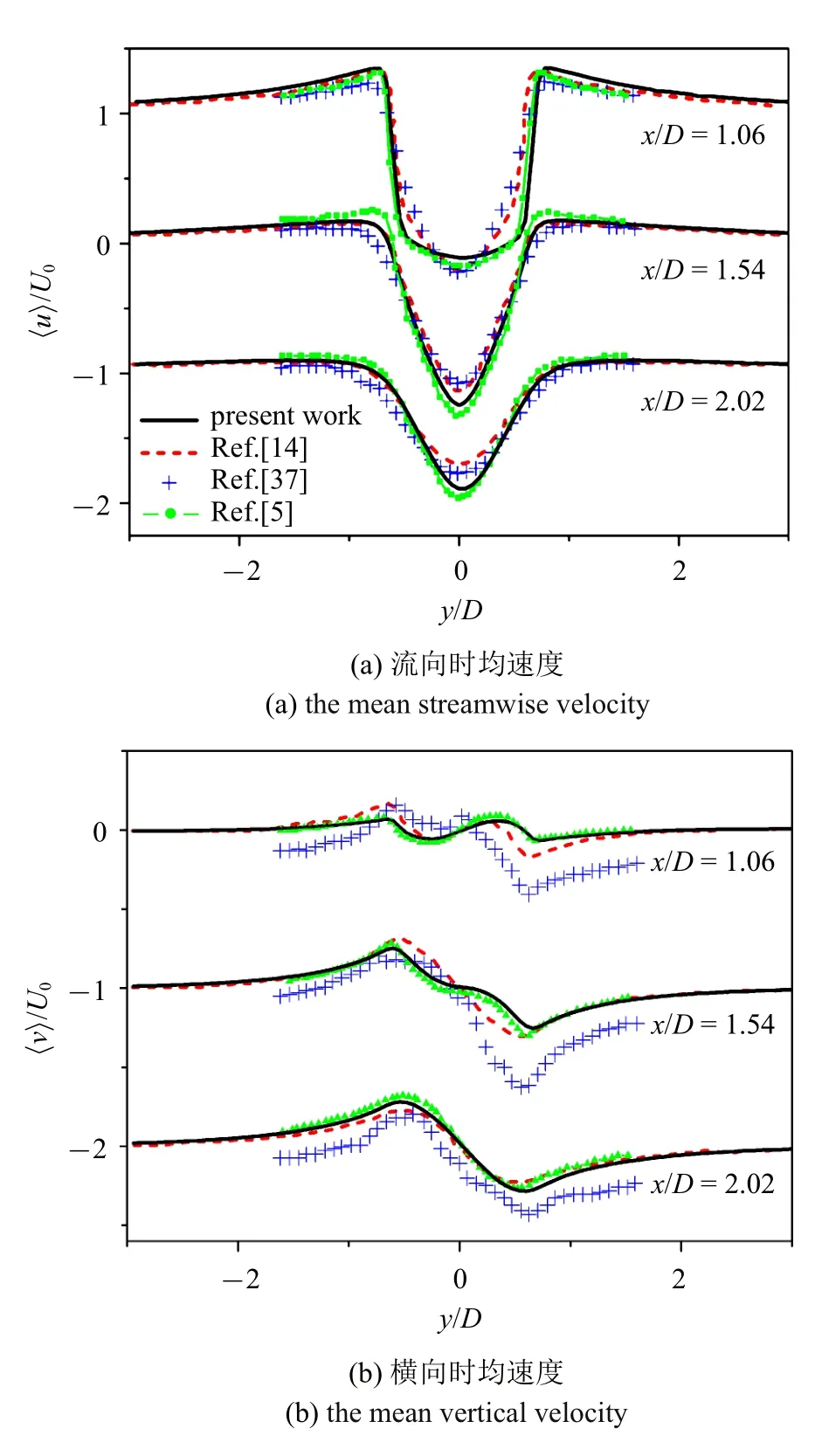
图4 时均速度在不同的流向位置(x/D=1.06,1.54,2.02)分布Fig.4 Vertical profiles of the mean streamwise and vertical velocity at x/D=1.06,1.54,2.02
图4 给出了3 个不同流向位置的时均一阶流向速度和横向速度的对比情况.如图4(a)所示,时均流向速度与前人的实验[5,37]和模拟[14]数据吻合很好.无磁场情况下,Moin 等[29]认为平均流向速度剖面的形状与剪切层的早期转捩密切相关.随着截面离圆柱距离的增加(x/D=1.06 ∼2.02),速度剖面的形状由“U” 字型转变成“V” 字型.“U” 字型速度剖面反映了两个完整的二维自由剪切层存在于横向坐标y/D=±0.5 处,并与圆柱后方回流区相结合.而在下游更远处(x/D=1.54),模拟结果显示的均是一个“V”字型速度剖面,说明该位置之后自由剪切层已在很大程度上被湍流运动破坏[38].
图4(b) 表示横向时均速度的对比,由于反向旋转的涡对脱落,横向速度剖面呈反对称性.在x/D=2.02 截面上,可以观察到分别位于y/D=±0.5 两个大的峰值存在,这些峰值与上游的自由剪切层y坐标位置一样,暗示着涡结构脱落引起剪切层垂直振荡运动的存在.但Lourenco[37]的实验结果似乎与预期相差很大,中心线的速度不为零且不具有反对称性.这一异常现象表明Lourenco[37]的实验存在其他干扰,导致数据偏差.实验测量的流向速度比横向速度更加精确.例如实验得到的流向速度误差大约在5%,而横向速度误差超过了50%[6].本文的一阶统计量模拟结果与Parnaudeau[5]的结果相吻合.
2.2 雷诺应力分量
图5 展示了二阶雷诺应力分量在尾迹区域不同的横截面与前人实验[33,37]和DNS[14]对比.主要的波动区域趋于一致,但波动幅值差异比较明显.在近圆柱背部区域,由于不同研究工作的网格设计分辨率不同,会导致圆柱附近的湍流统计特性存在差异.这一现象在许多研究中也被发现,如Dmitry 等[16],Valerio等[39].当远离圆柱体时,这种振幅的差异会越来越小.现有的实验和直接数值模拟的数据能给定物理量一个大致合理的区间和趋势,本文的统计物理量均在合理的区间内.本研究中所考虑的速度剖面对比的不确定性在10%之内,这与Parnaudeau 等[5]的标准是一致的.在图5(a)中,可以看到⟨uu⟩曲线有两个明显的峰值,这是由于尾迹区域中脱落的主涡对结构导致的波动行为.在更远的下游,两个峰值区域明显变得更小且更宽,说明两个剪切层向下游移动中在y方向逐渐发展,然后进一步过渡到湍流状态,随着距离增大耗散越多.图5(b)中雷诺应力分量⟨vv⟩对比Tremblay[14]的模拟结果略有低估但是与实验[33,37]结果更为接近,同样地横向速度波动的变化在更远处逐渐减缓.平均雷诺应力⟨uv⟩ 与时均横向速度剖面相似,都具有反对称性,并且随着距离增加逐渐扩散.
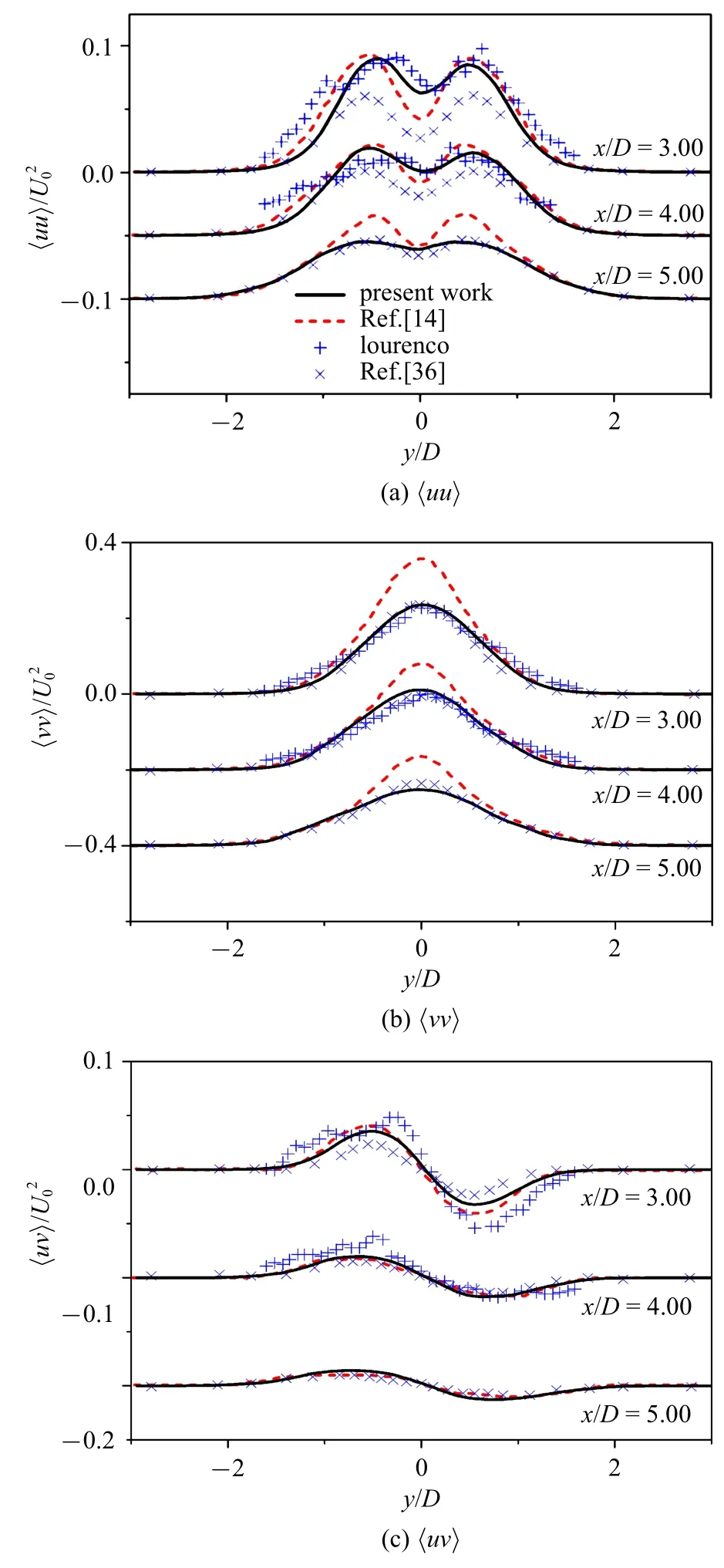
图5 时均雷诺应力分量在不同的垂直截面(x/D=3,4,5)分布Fig.5 Vertical profiles of the mean Reynolds stress components at x/D=1.06,1.54,2.02
表2 对比了当前DNS 结果与前人的研究结果,表明本文对于Re=3900 圆柱绕流湍流直接数值模拟的准确性与可靠性.

表2 Re=3900 工况下的圆柱绕流湍流实验和模拟工作−umin/U0Table 2 Experiments and simulations of the turbulent flow past a confined circular cylinder at Re=3900
2.3 流场结构分析
圆柱侧面无滑移边界产生扰动,引起边界层不稳定,并随来流进入尾迹而产生涡结构脱落.从图6(b)二维速度矢量图可以清楚地看到圆柱后方尾迹脱落的大尺度涡结构.在圆柱上下的剪切层中,由于剪切层的卷起和Kelvin-Helmholtz 不稳定性的产生,分离剪切层变得极不稳定,导致小尺度涡结构从圆柱体两侧的剪切层脱落,称为剪切层涡.

图6 圆柱附近的涡结构:(a)二维瞬时展向涡量云图;(b)二维瞬时速度矢量图Fig.6 Two dimensional vortex structures near the cylinder:(a)Two-dimensional instantaneous vorticity magnitude contour;(b)two-dimensional instantaneous velocity vector contour
这种小尺度涡脱落的位置近似地对应自由剪切层从二维流动状态过渡到三维的开始.为了正确地再现近尾流中的物理现象,最重要的是使圆柱两侧剪切层得到良好的解析.图6(a)是展向涡量云图,可以看出尾迹的脱涡方式为类似正负交替的卡门涡街.两个剪切层产生反向涡结构,在剪切层末端产生清晰的大尺度涡结构,随流动向下游移动并逐渐被耗散成无规律的形状.
3 磁场下圆柱绕流湍流分析
3.1 流向磁场下速度场
将无磁场情况的结果作为初始条件,本文计算了不同强度流向磁场对流场结构的影响,Ha分别为20,40,80.圆柱后方中心线的平均流向速度在不同的流向磁场作用下变化趋势如图7(a) 所示.圆柱后方存在负速度的回流区,随着磁场的增大,回流区被逐渐拉长.小磁场情况下(Ha=20)回流区内速度的峰值增大,但继续增大磁场(Ha40),峰值开始减小,回流区变得更加平缓.同时回流区的峰值位置也随着磁场增加向下游移动,当Ha=80,主回流区内无明显峰值.在回流区位置之后,中心线上速度逐渐攀升到稳定值,而且磁场影响下的尾迹区稳定值明显比无磁场情况的速度小.如图7(b)所示,随着流向磁场的增加,回流区长度线性增长.

图7 不同磁场强度下的变化Fig.7 Change under different magnetic fields
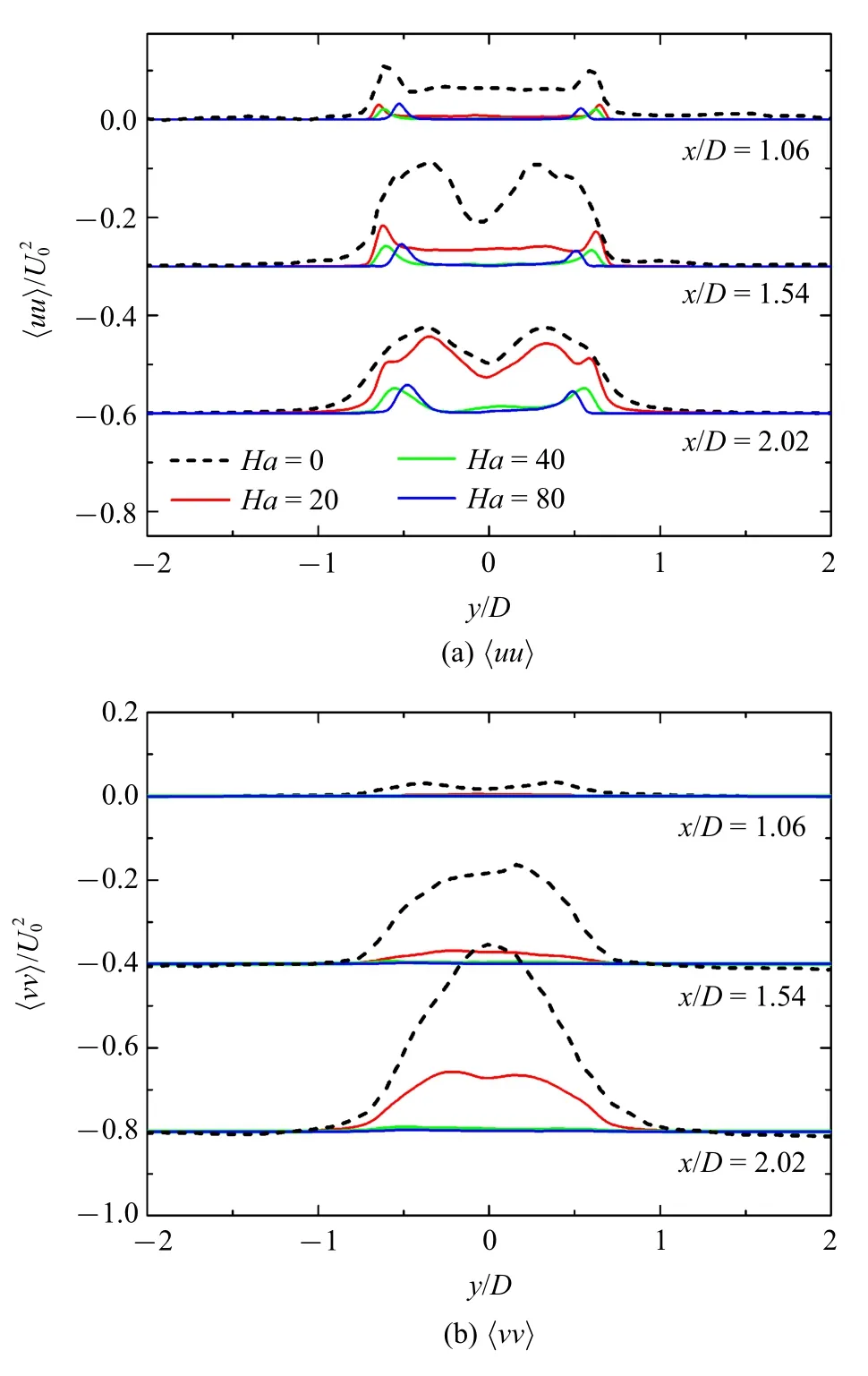
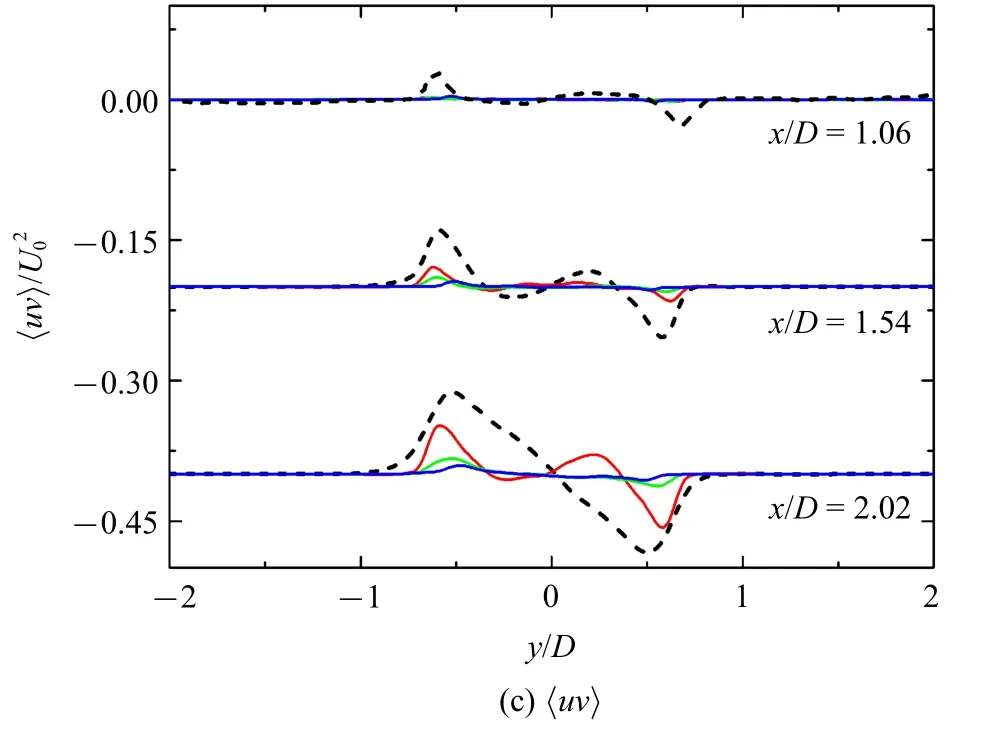
在磁场作用下,圆柱附近沿x轴三处截面位置的平均流向和横向速度分布如图8 所示.与无磁场情况相比,磁场作用下圆柱正后方(−0.5 图8 磁场下时均速度在不同的垂直截面分布Fig.8 Under different magnetic fields,vertical profiles of the mean velocity 同样地,磁场作用下的二阶统计量在下游3 个位置处(x/D=1.06,1.54,2.02)也有相应的趋势.图9(a)表明圆柱上下两个剪切层中,脱涡结构导致这个区域有两个明显的峰值.除了抑制效应,流向磁场的增强也使得两个峰值区域逐渐趋近圆柱后方中心线. 磁场作用下产生的洛伦兹力使流向涡结构强度减弱,并且在垂直方向上挤压尾迹涡,使其由两侧向中心靠近.横向速度脉动(9(b)) 和雷诺剪切应力(9(c)) 同样受到了磁场的抑制作用.从图9(c) 也可以观察到反向的涡对在磁场作用下相互靠近,但强度减弱. 在图10 中,瞬时流向速度及涡结构等值面(Q=1) 的分布形态展示了磁场力的影响.磁场作用下产生的横向洛伦兹力会抑制剪切层的卷起和Kelvin-Helmholtz 不稳定性的发生,致使剪切层变得更加平稳并在流向方向被拉长.瞬时流向速度分布直观证实了洛伦兹力对尾迹涡的横向挤压作用,同时证明了不同截面上二阶速度脉动统计量曲线图峰值随着磁场增加而相互靠近. 图9 磁场下时均雷诺应力分量在不同的垂直截面分布Fig.9 Effect of magnetic field on the mean Reynolds stress components at the different vertical profiles 图10 磁场下瞬时流向速度云图及涡结构等值面(Q=1)分布Fig.10 The instantaneous streamwise velocity contour and vortical structure,identified by the Q–criterion(Q=1) 图10 磁场下瞬时流向速度云图及涡结构等值面(Q=1)分布(续)Fig.10 The instantaneous streamwise velocity contour and vortical structure,identified by the Q–criterion(Q=1)(continued) 本文通过DNS 模拟了无磁场下次临界雷诺数Re=3900 圆柱绕流湍流,可以清晰观察到圆柱后方尾迹正负交替的类卡门涡街结构.由于Kelvin-Helmholtz 不稳定性,圆柱体两侧剪切层失稳,小尺度涡脱落.一阶二阶湍流统计量,如速度,雷诺应力等均与前人的实验及模拟结果吻合很好,表明了程序的准确性和网格的合理性.在无磁场充分发展的基础上,施加不同强度流向磁场,计算结果表明:流向磁场对一阶速度场和二阶雷诺应力都具有抑制作用,流场的湍流度降低.横向洛伦兹力会抑制Kelvin-Helmholtz 不稳定性,圆柱附近自由剪切层在磁场的作用下被拉长变得平稳.而且随磁场增强,圆柱后方的回流区被逐渐拉长,回流区速度减弱,流动更加趋于线性化.同时流向磁场产生的横向洛伦兹力使得涡街受到挤压,尾迹变窄.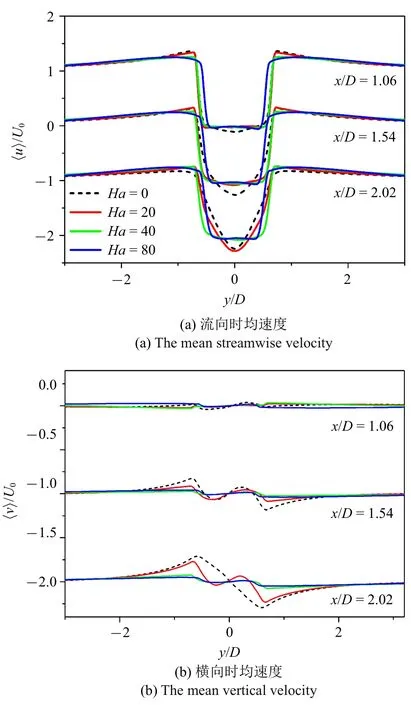
3.2 流向磁场下二阶雷诺应力分量
4 结论


