低雷诺数沟槽表面湍流/非湍流界面特性的实验研究1)

李思成 吴迪 崔光耀 王晋军

(北京航空航天大学流体力学教育部重点实验室,北京 100191)

引言

湍流/非湍流界面指的是流场中湍流区域和包围湍流的无旋流动区域的边界,其广泛存在于射流、尾流、混合层、湍流边界层等湍流流动中.在穿过这一层很薄的湍流/非湍流界面中,包含了多尺度的复杂结构,在无旋流和湍流之间的物质、动量和能量交换中起到主导作用,因此对界面特性的研究有助于对湍流发展过程的理解和预测.针对湍流/非湍流界面的研究主要集中在界面的几何特性[1-4]和动力学特性[2,5-7]两方面.

界面的几何特征主要包括界面的高度分布、沿垂向间歇因子分布及界面的分形维度等.Corrsin 和Kisteler[8]指出,间歇因子分布的导数就是界面高度的概率密度分布,因此这两个分布密切相关.Borrell和Jim´enez[3]的研究指出,界面高度的分布受到识别界面时阈值选取的影响.由于越靠近壁面无论是涡量还是湍动能都会增大,因此常用的涡量阈值或是湍动能阈值方法,所得界面平均位置都会随阈值增大而降低.De Silva 等[1]研究了界面的分形维度,发现在高雷诺数的情况下分形维度Df≈2.3,且受雷诺数、界面识别的阈值选取影响较小.Wu 等[4]得到Df=2.22比De Silva 的结果略小.张爽和时钟[9]的研究也表明随着湍流强度的减弱,界面形状会更加平滑,分形维度也相应地减小.

对于界面的动力学特征,研究包括流场中穿过界面或在界面附近的速度、涡量等物理量的相关特性.Corrsin 和Kisteler[8]最早发现,穿过界面的速度大小存在一个阶跃变化.湍流/非湍流界面简单的说是湍流与非湍流的分界面,但这不是一个严格的空间曲面界限,而是一个很薄的空间范围,Bisset 等[5]对平板远场尾流的研究表明速度和展向涡量在界面附近的跳变集中在尾流宽度10%的范围以内.Chauhan等[2]在其研究中采用了流向速度跳变量与当地的流向速度梯度之比作为湍流/非湍流界面厚度的定义,发现流向速度、展向涡量及雷诺应力均在界面厚度范围内发生跳变.

相对于光滑平板湍流边界层湍流/非湍流界面特性的研究,对非光滑壁面、特别是具有重要应用前景的减阻沟槽表面湍流边界层湍流/非湍流界面特性的研究工作相对较少,对其界面湍流扩散的影响亦缺乏了解.众所周知,顺流向的沟槽表面在适当的条件下通过改变近壁面流动结构降低了壁面摩擦阻力[10-17].Bechert 等[18]研究发现在沟槽内尺度无量纲间距s+为15 ∼20,深宽比h/s为0.5 ∼0.8 时最大减阻率可达10%左右.杨绍琼等[19]及袁一平等[20]也在相近的尺度范围内得到了最佳的沟槽减阻效果.Koeltzsch 等[21]发现发散−汇聚型沟槽在特定情况下也能够减小阻力的现象引发了很多关注.崔光耀等[22]通过研究发现发散型沟槽能够减阻的原因主要是沟槽引起局部顺向涡的减少.Kevin 等[23]在汇聚−发散型沟槽壁面上流动的研究中发现壁面加强了湍流/非湍流的掺混程度,发散型沟槽表面上湍流区域中的非湍流块出现的概率是光滑壁面和汇聚型沟槽壁面的两倍.Wu 等[4]指出汇聚型和发散型沟槽分别具有增阻和减阻的作用,而对应的湍流/非湍流界面高度概率密度分布相对于正态分布分别存在正的和负的偏度.

本实验主要采用时间解析的二维粒子图像测速技术(PIV) 对光滑和顺流向沟槽平板湍流边界层流场进行测量,研究低雷诺数沟槽表面对湍流边界层湍流/非湍流界面的影响.本文第1 节为实验仪器设备、实验模型、实验参数的介绍,第2 节对测量所得流场进行分析,主要包括湍流边界层摩擦速度的确定、湍流/非湍流界面识别、界面的几何特征和动力学特征,第3 节为论文的结论.

1 实验设置

本实验在北京航空航天大学的低速回流式水槽中进行,水槽实验段的侧壁和底壁均由光滑的有机玻璃制成.实验段几何尺寸为3 m×60 cm×70 cm(长×宽×深),实验采用的模型为光滑平板、精细的顺流向沟槽平板,模型尺寸均为长2.4 m,宽60 cm,平铺在水槽实验段中.

图1 给出了沟槽模型的示意图,沟槽截面形状为锯齿形,其齿间距为s,沟槽深度为h,顶角为α.由于数据来自两次实验,具体参数稍有不同,详情可见表1.齿根部位以小圆弧过度,以便给铣刀加工留够空间.实验模型前端加装坡度比1:10 的与平板宽度、厚度相同的斜劈,用以避免来流在模型的钝体前缘发生分离.模型平板前端还放置了直径3 mm 的拌线用来加速流动转捩,以保证下游实验数据采集区域处于充分发展的湍流状态.本文中实验坐标系的x,y,z轴分别对应流向、垂向和展向方向,对应的流速分别用u,v,w表示.对于光滑壁面和沟槽壁面的模型,坐标y轴的原点分别建立在光滑壁面的表平面和沟槽壁面齿顶所在平面上.

本实验采用PIV 技术对不同雷诺数下光滑、沟槽平板湍流边界层进行测量,通过改变来流速度U∞来使得雷诺数Reτ在400 ∼1000 范围变化.实验中采用连续激光照亮示踪粒子,激光片光厚度约为1 mm.示踪粒子采用的是直径为5 ∼20 µm的空心玻璃珠,密度为1.05 g/cm3.拍摄视野的中心位于从斜劈前端算起的下游2 m 处,激光平面垂直于模型表面并平行于来流方向,即位于Oxy平面内.激光平面位于水槽的中心对称面上,距离水槽侧壁有足够的距离(30 cm),因此可以忽略侧壁边界的影响[4].采用CMOS 相机采集粒子图像,相机的像素为2048×2048,测量视野的大小为120 mm×120 mm,因此空间分辨率约为每像素0.059 mm.实验中根据来流速度的变化,采用了不同的采样频率fs(表1),以尽量保证相邻两幅粒子图像中最大的粒子位移约为8 ∼12 个像素.由于CMOS相机内存的限制,单次采样连续采样时间受限,因此每个工况重复采样5 次,以保证统计数据收敛.速度场计算采用了MILK 算法[24-25],查询窗口大小为32×32 像素,重叠率为75%.

图1 沟槽模型简图Fig.1 Riblets plate model in experiment

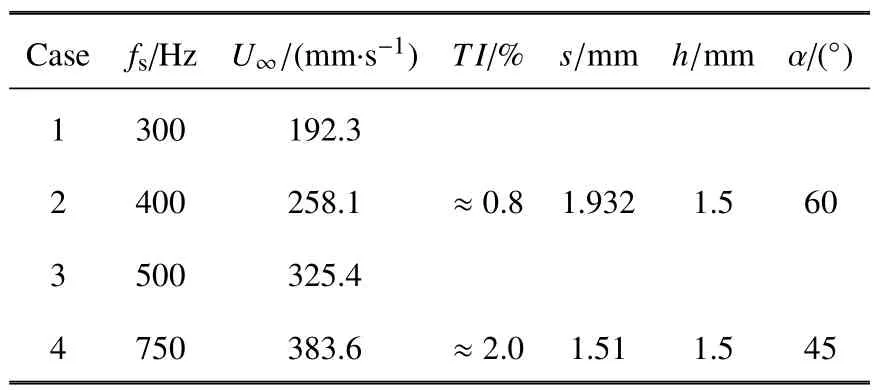
表1 各组实验模型参数及流场条件设置Table 1 Parameters of models and flow field of each case

2 实验结果与分析

2.1 摩擦速度

本实验中无法直接测量模型壁面某处的摩擦阻力,因此采用Clauser[26]的方法拟合摩擦速度uτ,以此衡量模型表面阻力大小.然而对于沟槽表面来说,一般认为其理论零点会低于沟槽齿顶平面,传统的Clauser 拟合方法失效了.针对这一问题人们常采用修正的Clauser 方法:对于沟槽表面的速度型在对数区满足

通过迭代计算可以同时得到摩擦速度uτ和理论零点yv的值.本文也采用了Choi[27]研究中采用的方法,他认为无论平板表面是何种类型的粗糙,以yuτ/δ∗U∞来表示的无量纲高度在0.002 ∼0.15 范围时,无量纲速度亏损(U∞−u)/uτ在粗糙表面上的分布应与其在光滑表面上的分布相吻合.根据实验数据得出Reτ≈1000 的拟合结果如图2(b)所示,其中yv=0.8 mm,uτ=16.0 mm/s.这两种方法本质上都假设沟槽表面上的速度同样服从对数分布,修正的Clauser 方法在低雷诺数下使用时常遇到多解的问题,此时可与Choi 方法结合使用,相互印证,提高结果准确性.本文中为表述方便,图片及下文中均直接用符号y来表示理论法向高度.

图2 Reτ ≈1000 组对数速度型及速度亏损曲线Fig.2 Velocity profiles and Velocity defect profiles for Reτ ≈1000

通过与Bechert 等[18]研究中沟槽减阻效果比较,可以确定摩擦速度uτ结果的合理性,如图3 所示.其中,∆τ 是沟槽表面和光滑表面摩阻应力之差,负值表示沟槽表面相对于光滑表面有减阻效果,正值则表示阻力增大的情况.τs是光滑表面上的摩阻应力,由于τ=,因此在得到uτ后就可以算出.本实验中改变雷诺数进而影响了无量纲间距s+,使得沟槽表面分别出现了阻力增大、减小的情况.从图3 可以看出,本文的实验结果与Bechert 等[18]直接改变沟槽几何尺寸得到结果的变化规律相吻合.

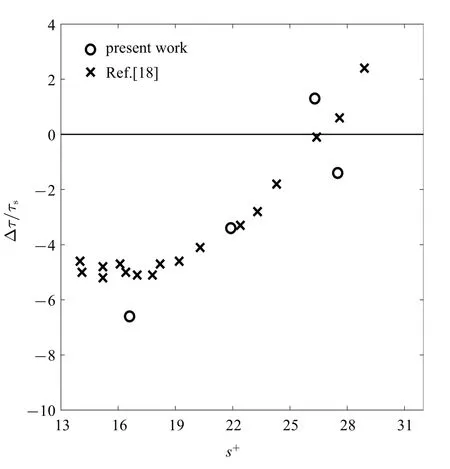
图3 不同无量纲齿距下的增减阻情况Fig.3 Drag reduction at difference dimensionless distances of riblets

2.2 界面识别

湍流/非湍流界面通常采用流场中某个物理量的大小作为一个阈值来提取其等值面作为界面,例如采用速度大小、涡量大小,或者PIV 中粒子浓度的等值面等方法.在直接数值模拟中,由于可以采用空间分辨率较高的网格且湍流度可以控制得非常低,以及没有背景噪声,涡量的计算相对准确,人们常采用涡量阈值判则识别湍流/非湍流界面.在实验研究中,往往很难到达精确计算涡量场的空间分辨率及消除背景噪声,因此Chauhan 等[2]提出的湍动能阈值判则更为实用.他们把局部湍动能定义为

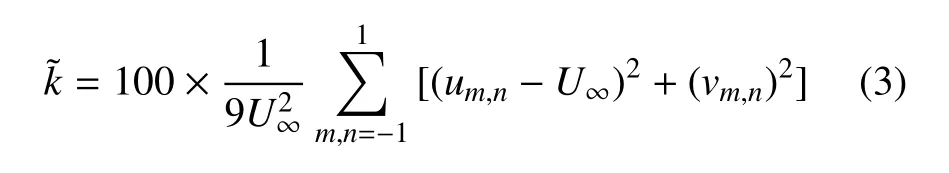
式中,u,v分别为流向、垂向速度分量,并将所求点周围3×3 网格点上湍流能的平均值作为该点的湍动能值,最后以来无量纲化并乘以100,这样,当测量点位于湍流/非湍流界面以外时,的值会非常接近当地的湍流度,而随着测量点逐渐靠近壁面,的值总体上会逐渐增大.取一个值的作为阈值,湍动能场中这个阈值对应的等值线就是要找的湍流/非湍流界面.

Chauhan 等[2]给出了阈值选取的条件:(1) 湍流边界层间歇因子的分布应该服从高斯误差函数,(2)界面高度yi的均值Yi和标准差σi满足Yi+3σi≈δ,其中δ 是边界层厚度.这两个条件一般也可等价为界面高度的概率密度(p.d.f.)服从正态分布,一般而言,这里的界面高度仅统计主界面,即最长的连续界面曲线.图4 给出了本实验中Reτ=1011、湍动能阈值=0.21 所得结果,其中图4(a) 黑色实线即为湍流/非湍流主界面位置轮廓线,图4(b)所示为界面高度概率密度分布,可见其满足正态分布,符合Chauhan 等[2]给出的阈值选取条件.

2.3 界面几何特性

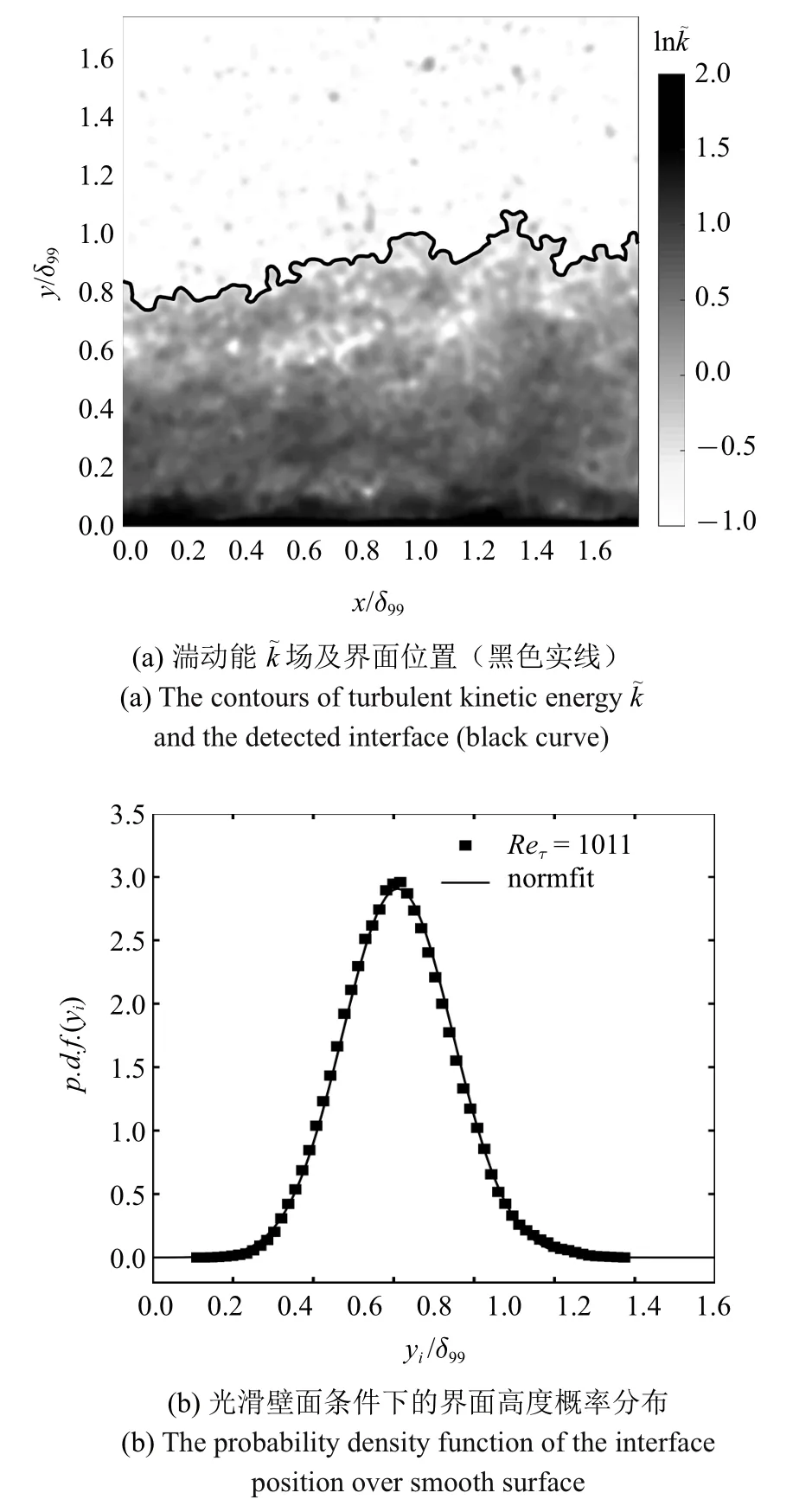
图4 湍流/非湍流界面识别结果(Reτ=1011)Fig.4 Example of detection results of the turbulent/non-turbulent interface for Reτ=1011

图5 界面平均高度与标准差随雷诺数的变化Fig.5 Mean height and standard deviation of the interface under different Reynolds numbers

本实验中所得界面分布的统计平均高度Yi/δ99如图5 所示,其中数据点上竖线的长度表示了该雷诺数下界面高度标准差σi/δ99的大小.与Wu等[4]、Corrsin 和Kistler[8]及Eisma 等[28]的结果相比,界面的无量纲平均高度与标准差是相近的.可以看到,界面高度Yi约为(0.8 ∼0.9)δ99且受雷诺数及壁面条件的影响均不大,沟槽壁面使得界面高度的标准差大于光滑壁面的情况,而Yi+σi基本保持在δ99附近.图6 中将沟槽壁面湍流边界层湍流/非湍流界面高度的概率密度分布与同来流速度光滑壁面上界面高度服从的正态分布(黑色实线)进行了对比.可以明显看到,在本实验条件下,在Reτ,riblets=996 时,界面高度分布呈现正的偏度,对应的壁面摩阻增大了1.3%,这与Wu 等[4]得到的汇聚型沟槽壁面造成摩擦阻力增大的情况下,湍流/非湍流界面会相应地呈现出正偏度的结果是一致的.

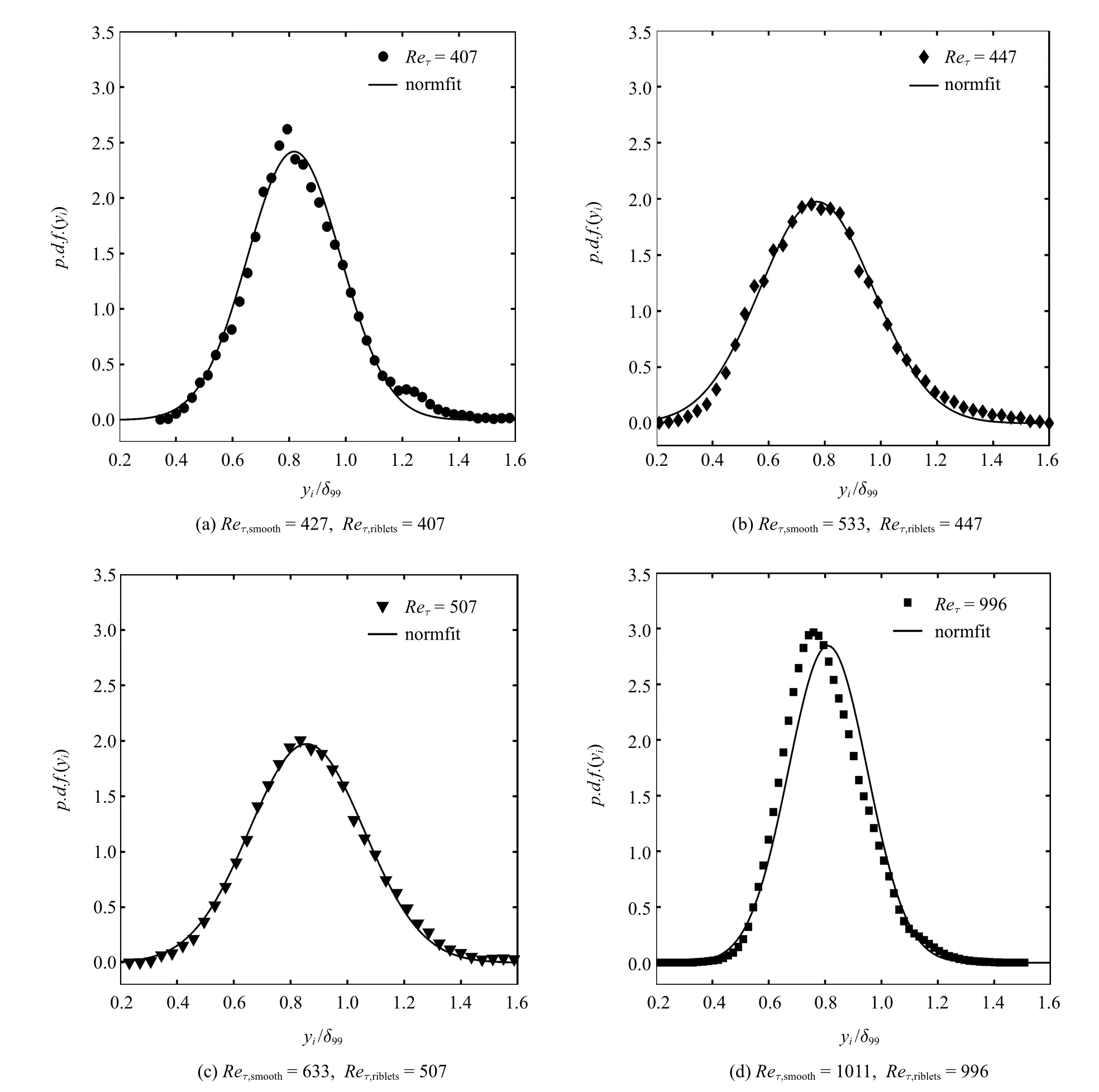
图6 各雷诺数下沟槽壁面条件下的界面高度概率分布Fig.6 Probability density functions of the interface position over riblets surface under different Reynolds numbers compared with the ones over smooth surface

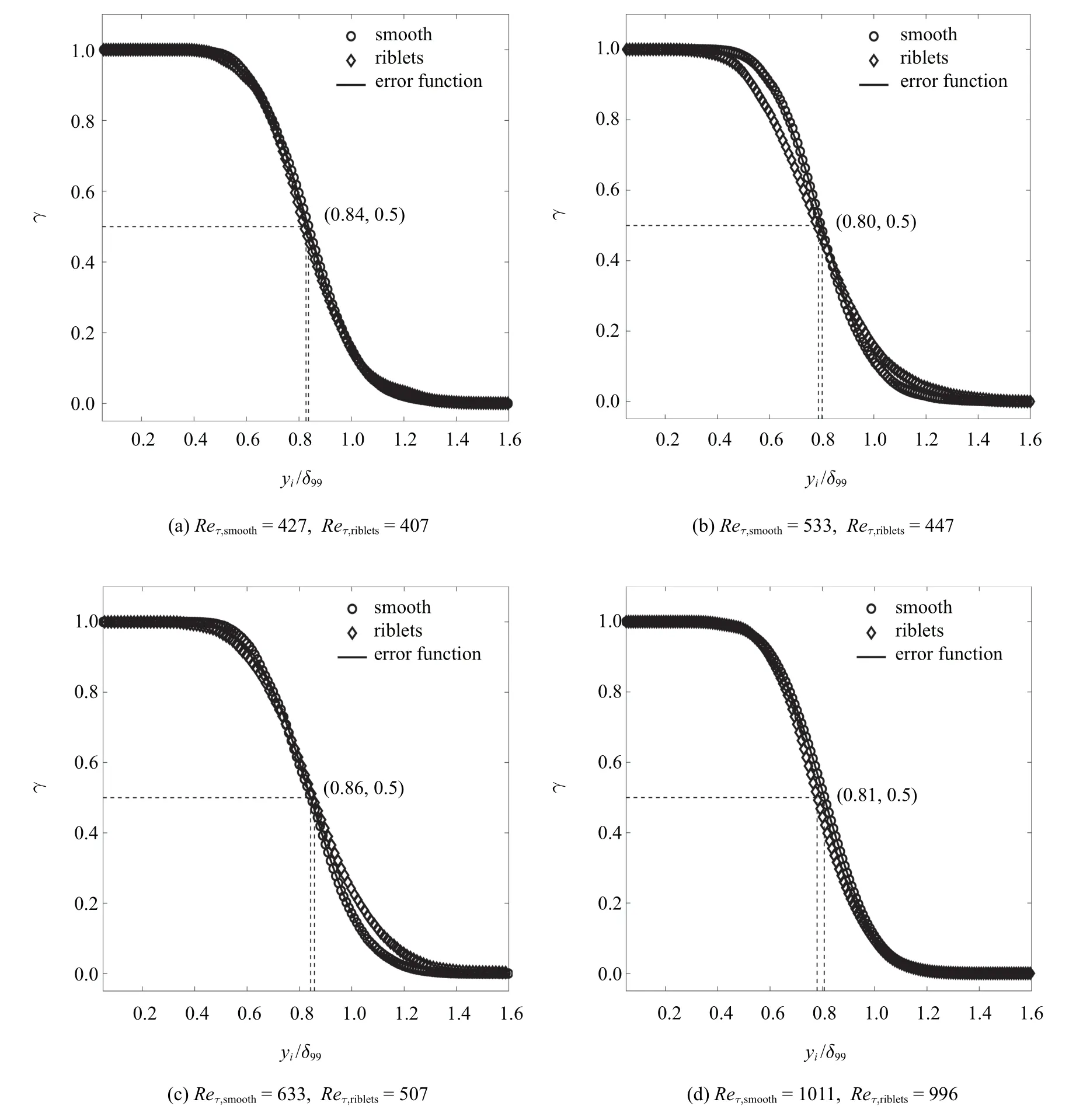
图7 间歇因子分布曲线Fig.7 Profiles of intermittency factor

在识别出湍流/非湍流界面所在位置之后,可以把流场以界面为界进行二值化,界面及界面以下的区域置为1,界面以上的区域置为0,这样对流场在同一垂向高度进行系综平均,就能够得到任意流向位置的沿垂向分布的间歇因子γ,如图7 所示.可以看到,光滑壁面条件下的间歇因子分布很好地服从误差函数,也印证前面提到的其界面高度分布服从正态分布的结果,即实质上对间歇因子分布的微分即可求得界面高度的概率密度分布.当沟槽壁面上界面高度分布的标准差相比光滑壁面上的大得多时,其间歇因子变化也相对更加平缓(图7(b)和图7(c)).γ=0.5 的位置表示湍流和非湍流出现概率相等的位置,对于界面高度服从正态分布的光滑壁面流动来说γ=0.5 的高度理论上就是界面平均高度,因此这里插值得到的γ=0.5 的高度与直接对界面高度求得的平均值相当接近.

Mandelbrot[29]首次猜测在高雷诺数下湍流中应该存在分形特征,而随后被Sreenivasan 等[30]首次在湍流/非湍流界面中发现.Prasad 和Sreenivasan[31]采取了一种盒计数算法来衡量湍流/非湍流界面的分形维度:将二维流场分割为边长为b/δ 的方形格子,并记录将界面曲线完全包纳进去的所需的最少格子数量N(b),改变方格边长b并重复上述操作,最后将不同帧所得结果求平均,就得到了包纳最少格数N与方格边长b的关系,在一定的范围内,格子边长b和最少格数N应该满足N∝(b/δ)−D,根据Mandelbrot和Wheeler[32]提出的共维准则(the co-dimension rule),三维分形维度Df=D+1.

图8(a) 中在对数坐标下绘制了Reτ,smooth=533(Reτ,riblets=447)时的b/δ99∼N的关系曲线,由于其满足指数型正相关,因此在虚线之间的范围内(b/δ99=0.04 ∼0.3)其关系近似一条直线,直线的斜率就是指数的幂,即−D.图8(b)绘制了不同壁面下湍流/非湍流界面分形维度随雷诺数的变化,图中还包括了Wu等[4]的结果.按照雷诺相似性假设和小尺度结构为Kolmogorov 尺度来预测可得分形维度[33]Df=2+1/3.Breda 和Buxton[34]认为界面分形维度与小尺度结构相关,当小尺度结构不为Kolmogorov 尺度时分形维度不一定为2.3 左右.可以看出,在Reτ小于1000范围内,Df呈增长趋势,界面的多尺度结构还没有充分发展.结合De Silva 等[1]的结果,可以推断湍流/非湍流界面分形维度约在Reτ大于2000 以后趋于Df=2.3.

2.4 界面动力学特性

为了明显地显示发生在湍流/非湍流界面附近的速度、涡量跳变,人们常常采用条件平均的方法进行分析:在某一时刻某一流向位置上,在界面所在高度位置建立一个新的坐标系,其原点落在界面曲线上,坐标轴与x,y轴分别平行,然后采集新坐标系下原点附近沿着y轴分布的速度矢量,作为一组速度样本.遍历每个时刻每个流向位置,将所得的所有速度样本整合在一起求系综平均,就得到了条件平均速度Uc.由于界面具有分形特征,界面曲线在流场中蜿蜒伸展,在同一时刻同一流向位置下可能会出现多个界面高度(参见图4(a)),针对这种情况,采用了仅取最低的界面位置建立新坐标系的方式,以保证在新的坐标中,垂向坐标的负半轴区域始终表示的是湍流区域[2,4].图9 给出了不同条件下的条件平均流向速度型,在(y−yi)/δ99=±0.1 以外的区域,流向速度梯度基本已经趋近于近似线性分布,湍流/非湍流界面以外接近势流区((y−yi)/δ99>0.1),流向速度梯度非常小,界面以内处于湍流区((y−yi)/δ99< −0.1),流向速度梯度相对大一些,并且在界面附近位置,流向速度梯度最大,即速度发生跳变.沟槽壁面使得界面处条件平均流向速度会有所不同,顺流向沟槽壁面的影响主要集中在界面附近及界面以内而很难影响到界面以外的区域.

采用Chauhan 等[2]的方法来估量名义界面厚度:先以远离界面位置近似线性的速度型的线性拟合与(y−yi)/δ99=0 轴的交点之距离作为速度跳变量∆Uc,然后以速度跳变∆Uc与速度最大梯度之比作为名义界面厚度δω,即

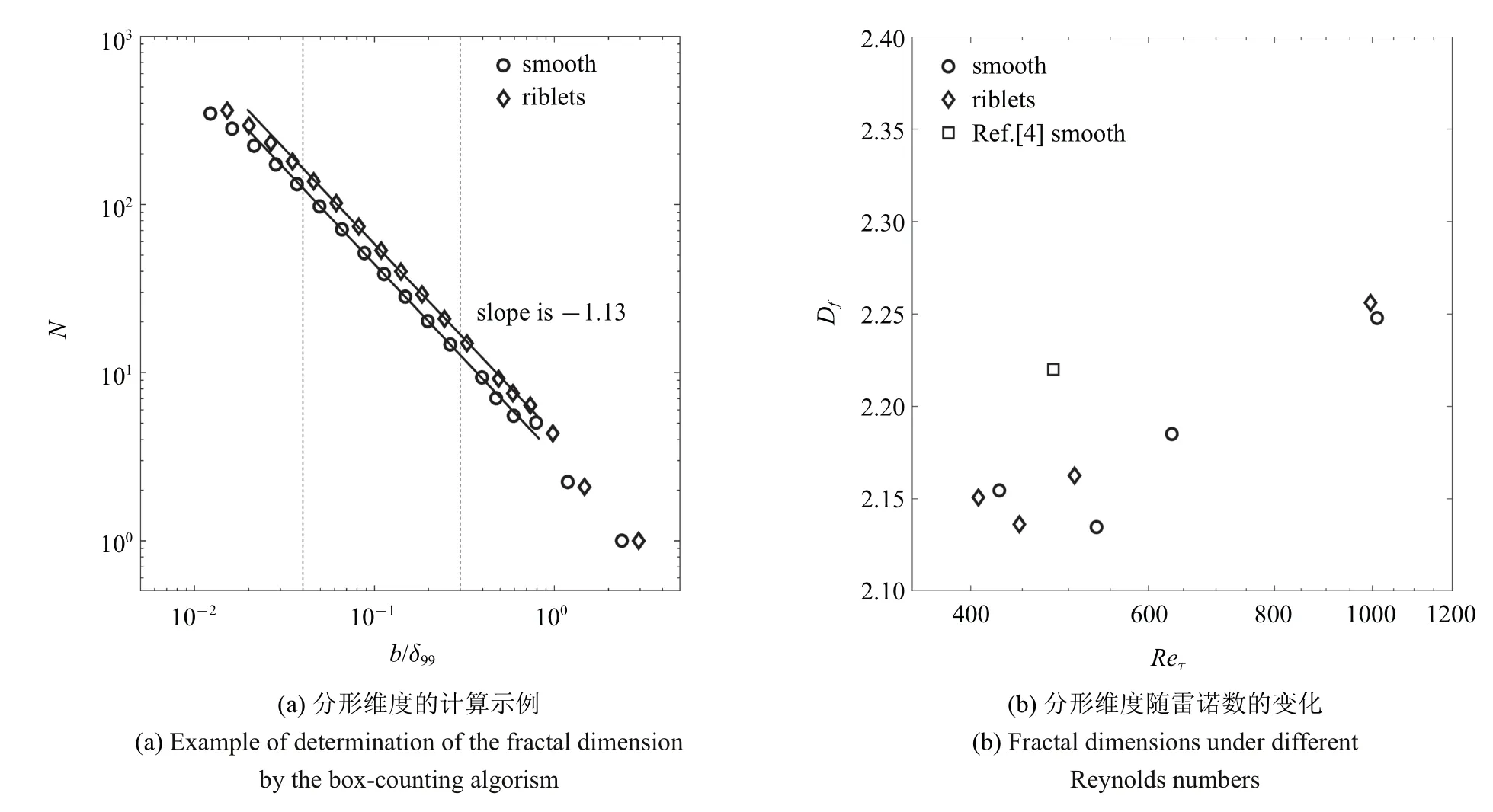
图8 不同条件下界面的分形维度Fig.8 The fractal dimensions under different conditions

图9 界面附近的条件平均流向速度Fig.9 Conditional averaged streamwise velocity profiles across the interface

图10 给出了条件平均流向速度跳变及最大速度梯度随雷诺数的变化.Chauhan 等[7]的研究表明∆Uc/uτ约为1.15 而不随雷诺数变化(Reτ2790).而本文的结果显示在雷诺数较小时,无量纲速度跳变存在随着雷诺数的增大而增大的趋势.条件平均的无量纲流向速度的最大梯度在雷诺数较小时近似为16 (如图10(b) 所示),但壁面形状的影响不明显.相应的无量纲界面厚度(如图11(a)和图11(b)所示)存在一个极大值,该极值点受沟槽影响会略小于光滑壁面的情况.

图12 绘制了条件平均的展向涡量分布,这里采用了简化的近似计算[2],由于垂向速度的梯度∂v/∂x相对于流向速度的梯度∂u/∂y小很多,在计算涡量时可以忽略不计,因此这里条件平均展向涡量ωz=∂Uc/∂y,因此图12 中无量纲涡量的峰值与图10(b)中条件平均流向速度最大梯度相应,从图12 也可以看出,当雷诺数较小时,其条件平均展向涡量分布是相似的.图中(y−yi)/δω=0 处的点画线对应条件平均坐标系下的界面位置,上下两条虚线分别位于(y−yi)/δω=±0.5 的位置,虚线包含的区域则是1 倍的界面厚度范围.无论是何种壁面条件、何种雷诺数,条件平均展向涡量的跳变基本都发生在1 倍界面厚度δω之内.远离界面位置向外,涡量逐渐减少并趋近于0,与外区流动基本为势流相适应,远离界面位置向内,涡量先减少后增加,越靠近壁面流动剪切越强,展向涡量也越大.

图10 条件平均速度在界面附近跳变Fig.10 The conditional averaged velocity jump across the interface

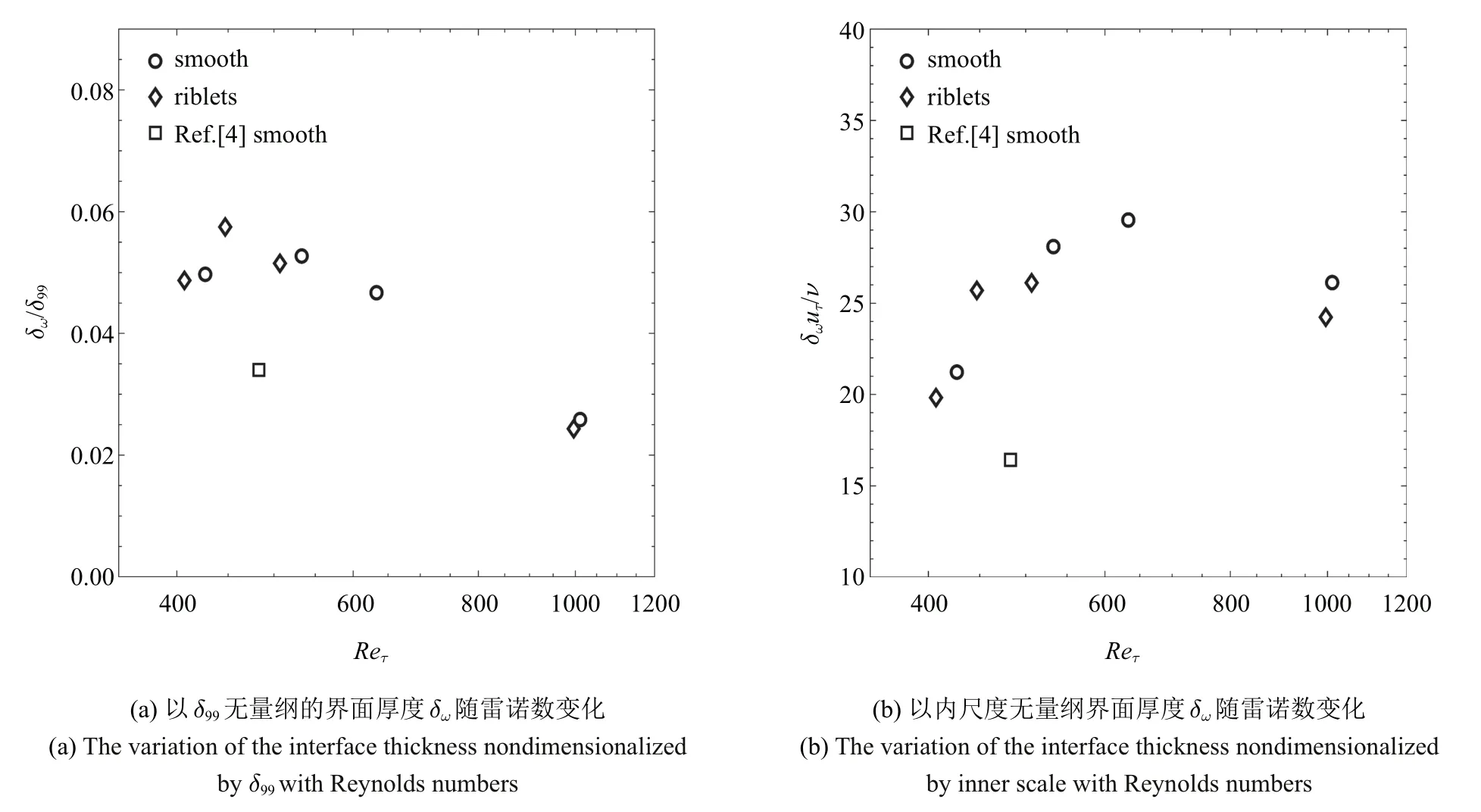
图11 无量纲界面厚度随Reτ 变化Fig.11 The variation of the dimensionless interface thickness with Reynolds numbers

图12 界面附近的条件平均展向涡量Fig.12 Conditional averaged vorticity across the interface

3 结论

本实验采用二维粒子图像测速技术技术对光滑、顺流向锯齿形沟槽表面湍流边界层流动在不同雷诺数下进行了测量,并着重研究和分析了雷诺数Reτ约为400 ∼1000 时通过湍动能方法识别的湍流/非湍流界面的几何特性和动力学特性,主要的结论如下:

(1) 湍流/非湍流界面的平均高度基本在(0.8 ∼0.9)δ99附近.截面为锯齿状的顺流向沟槽壁面在影响摩阻特性的同时影响了界面高度的概率密度分布,阻力增大的条件下界面高度的概率密度分布存在正的偏度,而在减阻情况范围时则基本呈正态分布.在雷诺数Reτ小于1000 的情况下,湍流/非湍流界面的分形维度会随着雷诺数的增大而增大,而壁面条件影响不明显.

(2) 跨越湍流/非湍流界面的无量纲速度跳变随雷诺数增大而增大的趋势,但壁面形状的影响不明显.在本实验雷诺数条件下,无量纲界面厚度随雷诺数的变化存在一个极大值,沟槽影响有降低该极值的趋势.此外,界面附近条件平均涡量分布具有相似性,受壁面形状和雷诺数影响很小.顺流向沟槽的壁面对于跨界面的速度跳变,条件平均涡量没有显著的影响.