一种鲁棒的HLLC格式及其稳定性分析
2020-12-23胡立军袁海专
胡立军, 袁海专
(1.衡阳师范学院 数学与统计学院,衡阳 421002;2.湘潭大学 数学与计算科学学院,湘潭 411105)
1 引 言
近几十年,基于Godunov方法的近似黎曼解法器在涉及激波和其他间断的可压缩流问题中取得了巨大的成功。主要包括Roe[1],HLL[2],HLLC[3],HLLEM[4]和AUSM-类格式[5-7]等。其中,HLL-类格式由于简单、精确、满足熵条件和保正性并且易于推广到不同的双曲系统而受到青睐。根据能否分辨线性波,可将其分成两类。一类是能够分辨线性波的全波HLL-类格式,包括HLLC,HLLEM,HLLE+[8]和HLLI[9],HLLEMS[10],HLLC-ADC[11]和HLLC-SWM[12]等,另一类是非全波HLL-类格式,包括HLL,HLLE[13],HLLS,HLLCM[14]和HLL-CPS[15]等。在计算剪切占优的流动现象、混合流体、燃烧面和物质界面时,需要使用全波HLL-类格式来求流通量。然而,在模拟某些超声速强激波问题时,全波HLL-类格式会出现各种形式的不稳定现象,尤其是carbuncle现象[16]。
Quirk[16]首先对数值计算中的激波异常现象进行系统分类,认为基于任何单一黎曼解法器的Godunov方法都会存在缺陷,并且提出了一种自适应的组合黎曼解法器。Gressier等[17]基于特殊的奇偶失联扰动分析和数值观察发现,格式的严格稳定性和精确捕捉接触波这两种特性是无法兼容的。Liou[18]认为质量通量独立于压力项的数值格式不会出现carbuncle现象,并且通过修正线性波的波速来设计一些激波稳定的接触捕捉格式。Dumbser等[19]利用矩阵方法研究稳态激波的稳定性,发现凸激波比凹激波具有更好的稳定性,并且上游马赫数越大稳定性越差。Shen等[14]认为格式的剪切粘性不足是诱发不稳定现象的唯一原因。
增加耗散已经成为改善激波异常现象的主流方法。Kim等[20]提出了一种HLLC-HLL混合方法,借助于开关函数,使得激波层内的横向通量由不稳定的HLLC转换成稳定的HLL,并且使用加权平均通量方法(WAF)来获得高阶精度。Huang等[21]在部分分量上对HLLC和HLL进行加权来消除不稳定现象。一些研究人员致力于开发真正多维的HLLC通量来抑制不稳定现象[22,23]。Rodionov[24]将N-S方程的粘性机制引入到无粘欧拉方程来消除Goudnov型数值格式的carbuncle现象。Chen等[25]在激波层亚声速区增加剪切波粘性来消除低耗散迎风格式的carbuncle现象。Xie等[26]通过压力控制方法来限制压力扰动的传播,进而治愈HLLC格式的不稳定性。Simon等[11,12]使用反扩散控制和选波修正两种策略来控制HLLC格式的耗散机制,进而抑制其不稳定性。
虽然研究人员对激波不稳定性开展了大量研究,但是仍然没有普遍接受的机理分析,这导致了很多改进方法都有一些局限性。本文结合小扰动分析方法和数值实验来研究HLLC格式的激波不稳定性,据此构造一种激波稳定的HLLC通量。一系列数值实验证明了新格式的鲁棒性和精度。
2 控制方程组
守恒形式的二维无粘可压缩欧拉方程组:
∂U/∂t+∂F(U)/∂x+∂G(U)/∂y=0
(1)
式中
(2)

(3)
(4)
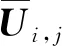
(5)
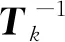
3 HLLC格式
Harten等[2]利用积分关系和 Rankine -Hugoniot 条件提出了一种简单的两波近似的HLL格式,其通量表达式为
(6)
左右波速分别为
(7)
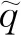
(8)
式中
(9)
(10)
式中k=L,R。
4 HLLC格式的激波稳定性分析
4.1 小扰动分析
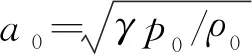
首先,在x-方向(纵向)添加奇偶对称扰动,扰动后的状态为
(11)
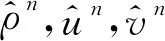
超声速(M0> 1)条件下,扰动的演化方程为
(12)

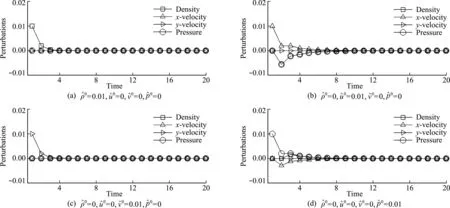
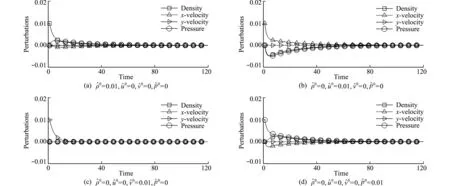
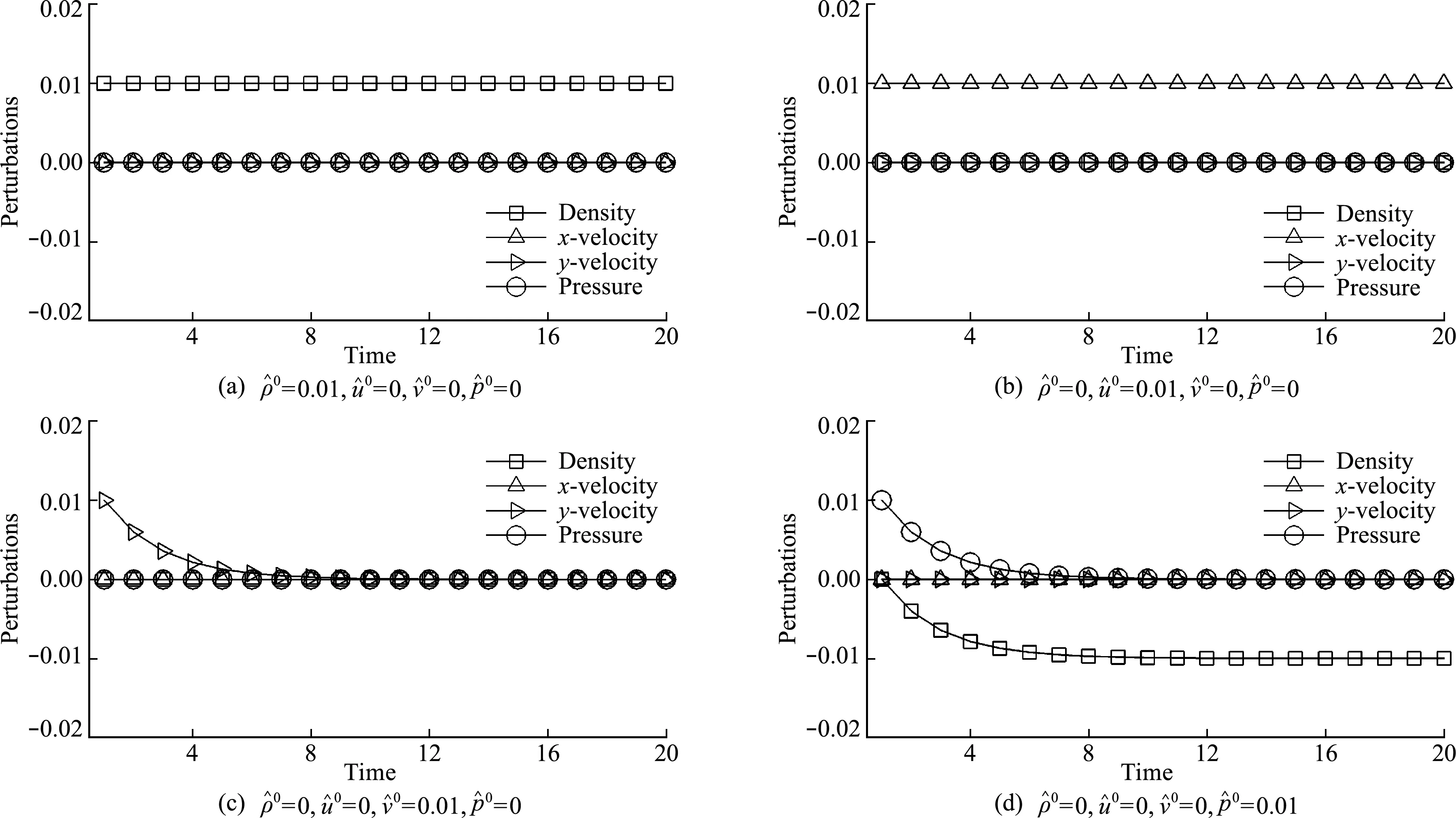
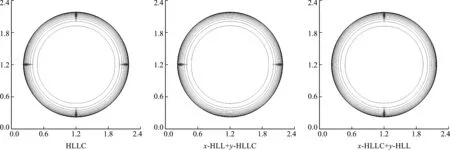
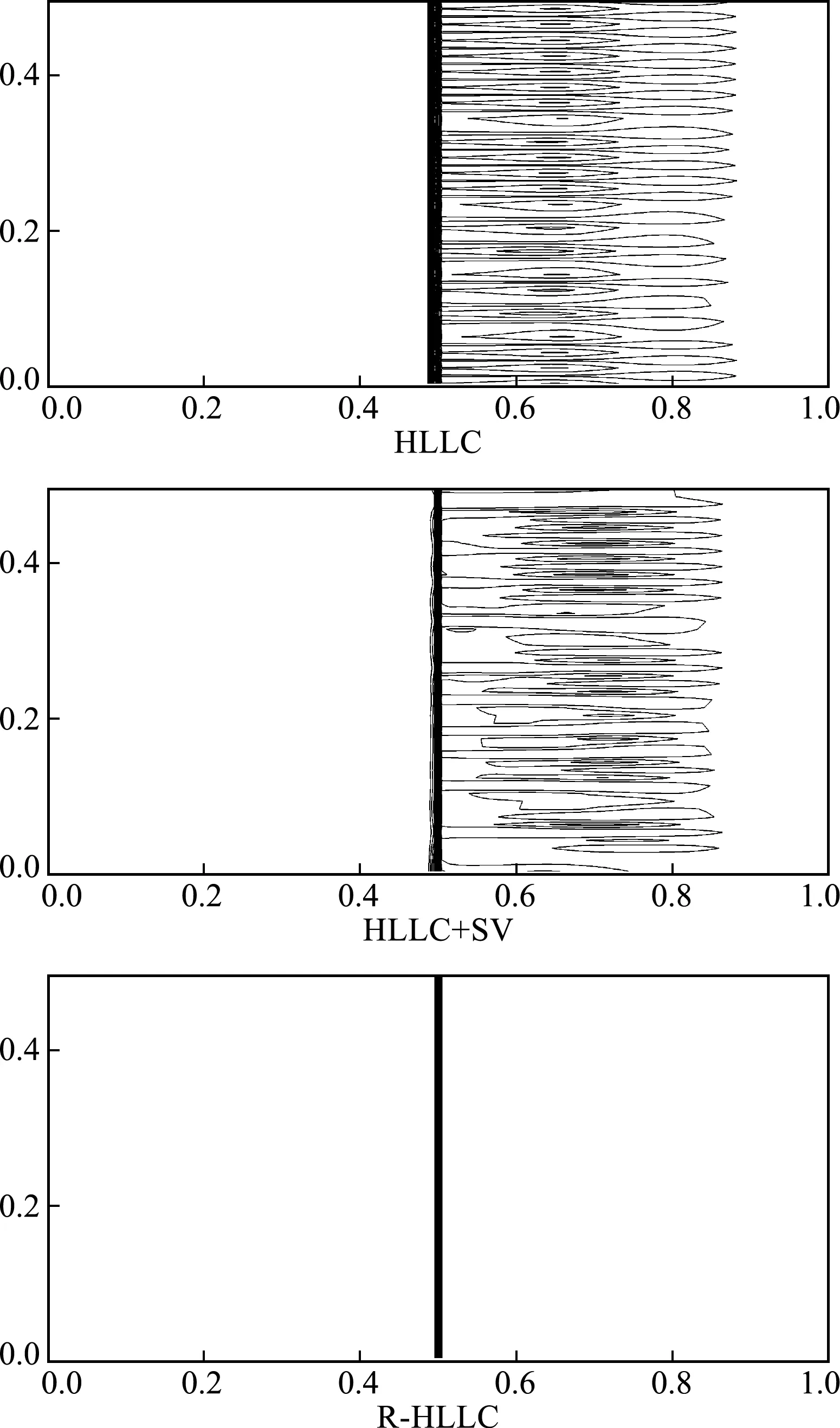
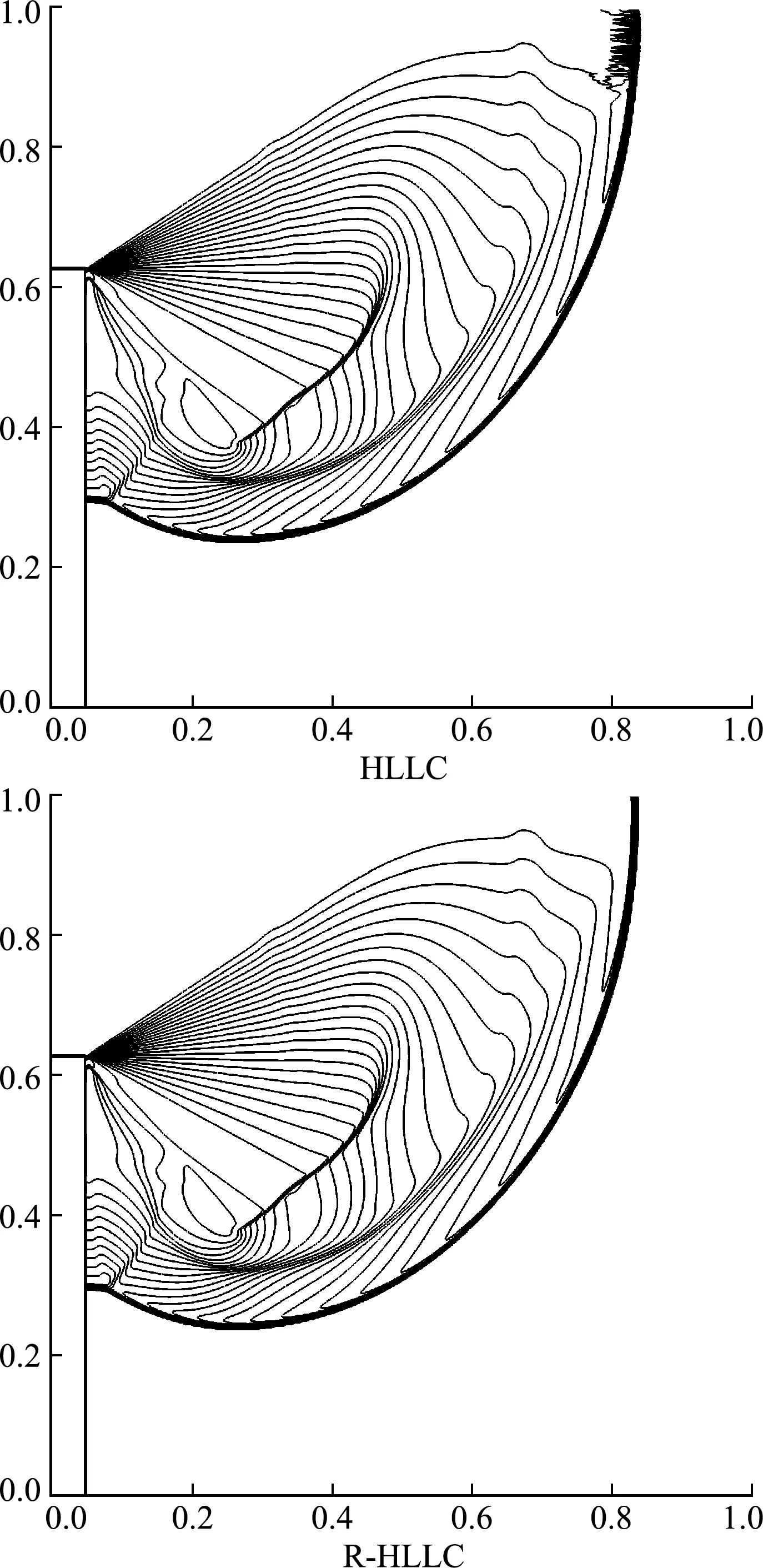
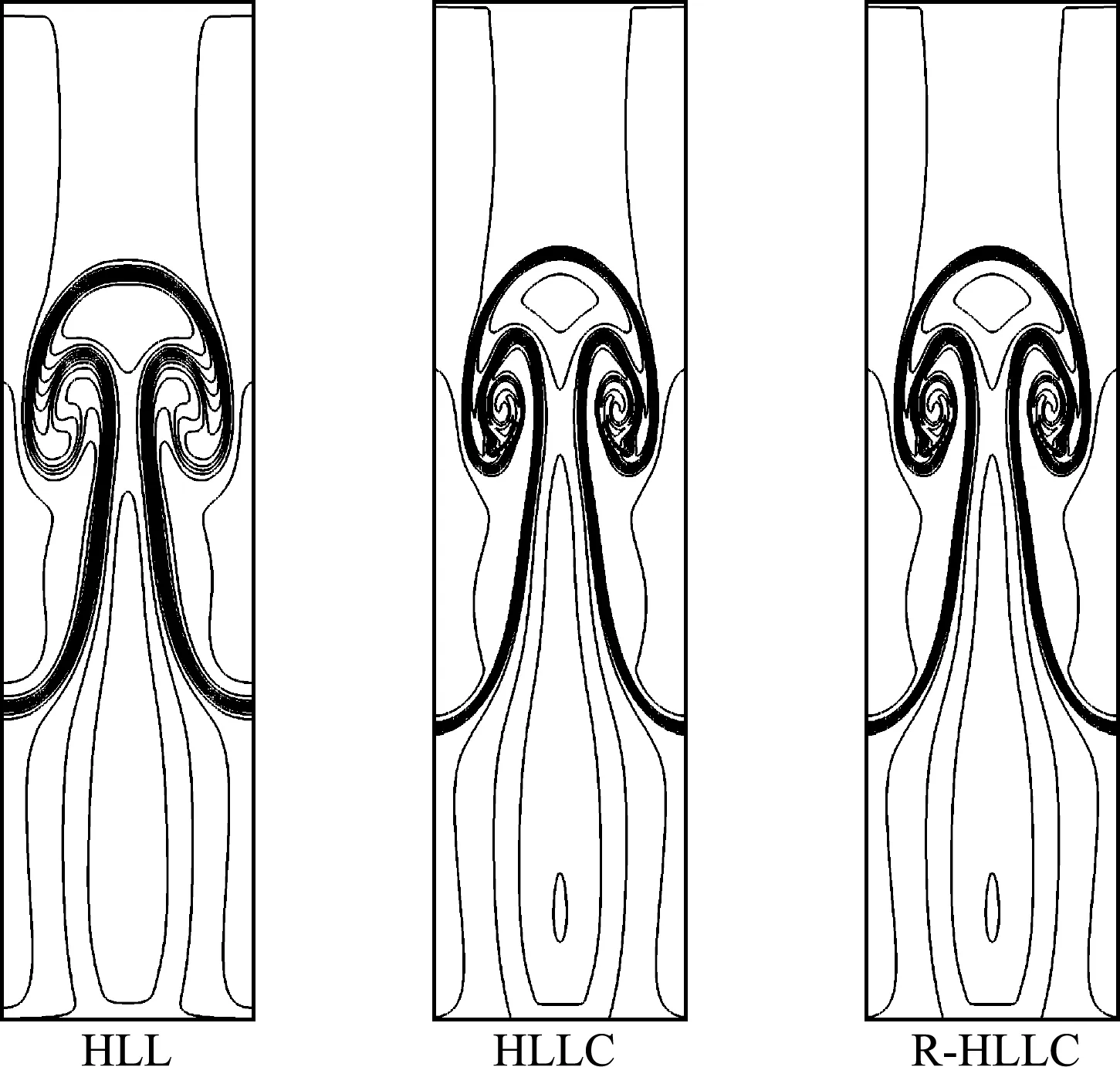
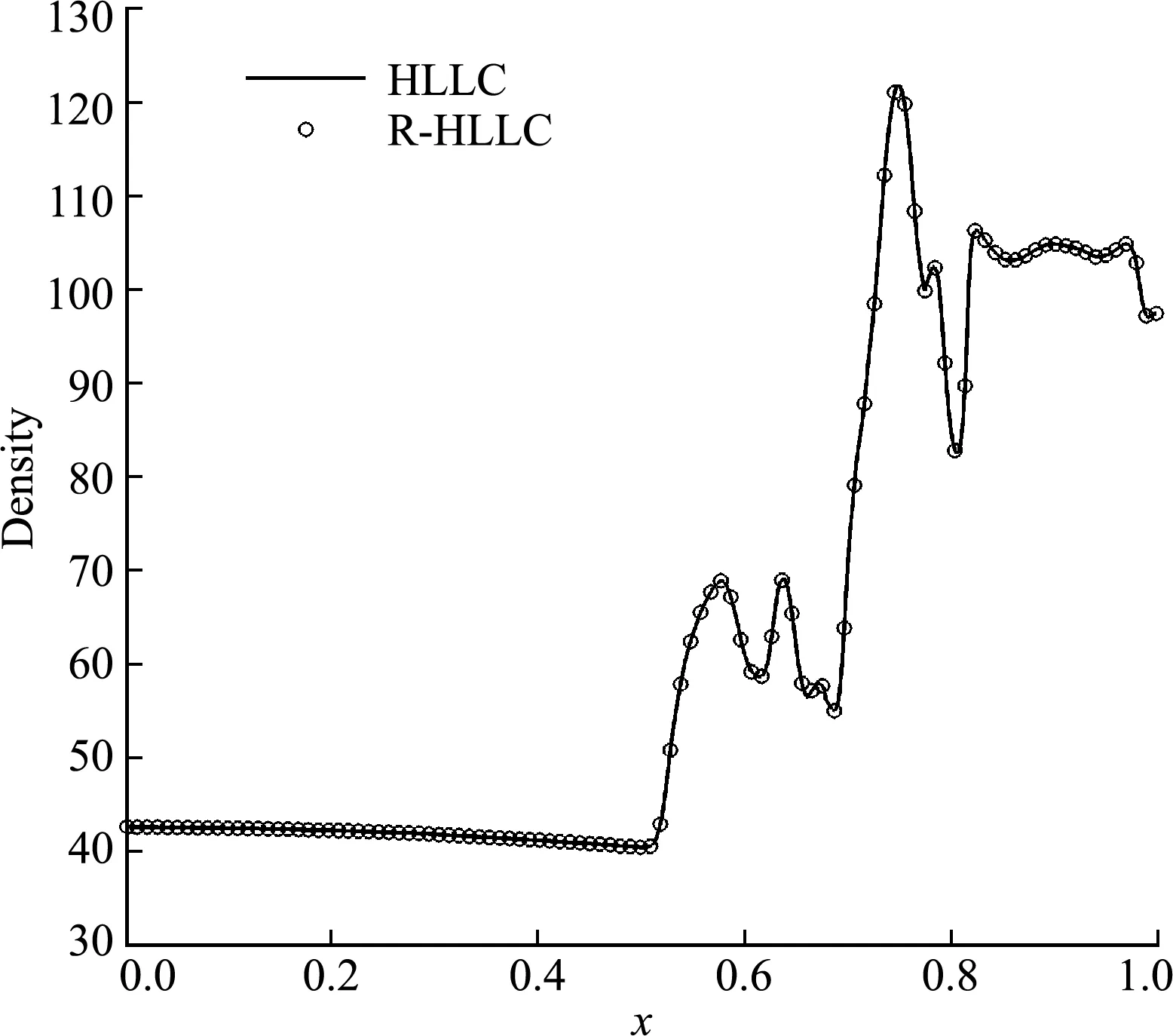
亚声速(0 (13) 接下来,考虑在y-方向(横向)添加如下奇偶对称扰动 (14) 采用HLLC格式计算y-方向的数值通量Gi,j + 1/2和Gi,j - 1/2,从而得到横向扰动的演化方程为 (15) 图1 超声速条件下纵向扰动的演化趋势 图2 亚声速条件下纵向扰动的演化趋势 基于4.1节的结论,在计算横向界面的数值通量时,增加熵波粘性和剪切波粘性来抑制HLLC格式的不稳定现象,具体表达式为 (16) 式中EV0和SV0分别为熵波粘性项和剪切波粘性项,Δq=qR-qL。 在熵波粘性项的单独作用下,横向扰动的演化方程为 图3 横向扰动的演化趋势 图4 二维Sedov爆轰波问题的密度等值线 (17) 此时,密度扰动可以有效衰减。在剪切波粘性项的单独作用下,横向扰动的演化方程为 (18) 此时,剪切速度的扰动可以有效衰减。因此只有在两者共同的作用下,横向所有物理量的扰动才能有效衰减,从而不会诱发不稳定现象。 在计算中,为了保留原HLLC格式精确分辨接触面和剪切层的优点,采用不需要引入经验参数的界面压力比来探测激波的位置[10], h= min. (pL/pR,pR/pL) (19) 上述分析表明,不稳定现象仅与横向界面的通量有关。在计算x-方向网格界面(i+1/2,j)的数值通量时,本文探测与其相邻的y-方向的四个界面是否处在激波层,反之亦然。即 hx= min. (hi,j - 1/2,hi,j + 1/2,hi + 1,j - 1/2,hi + 1,j + 1/2) hy= min. (hi - 1/2,j,hi + 1/2,j,hi - 1/2,j + 1,hi + 1/2,j + 1) (20) 利用余弦函数来定义开关函数 f= [1+cos(πh)]/2 (21) 在激波层内,由于存在压力差,所以0 Xu等[27]认为激波层超声速区的数值结构在扰动下是稳定的,但是亚声速区的扰动会放大,进而导致激波失稳,因此定义亚声速区探测函数[25] (22) 式中M为马赫数。显然,在超声速区g=0;在亚声速区0 考虑式(21,22),激波面横向通量上添加的熵波与剪切波粘性项可表示为 (23) 从而,一种鲁棒的HLLC(R-HLLC,Robust HLLC)格式的通量可表示为 (24) 由TEV和TSV的定义可知,计算强激波亚声速区的横向数值通量时,R-HLLC格式接近于两波近似的HLL格式;在其余的大部分地方,R-HLLC格式等价于HLLC格式。由于HLL格式和HLLC格式对于强激波的捕捉能力基本一致,因此局部增加横向通量的粘性不会导致计算结果的失真,后面数值实验的结果也说明了这一点。此外,Chen等[25]引入剪切粘性来抑制不稳定性。与其相比,本文在三个方面进行了改进,(1) 利用小扰动分析探究了不稳定现象的根源;(2) 仅在横向通量上添加粘性,而文献[25]在横向和纵向都添加了粘性;(3) 引入熵波和剪切波粘性来消除不稳定现象,而文献[25]只引入了剪切波粘性。数值实验的结果表明,单纯添加剪切粘性无法完全抑制不稳定现象。 通过典型算例来检验R-HLLC格式的性能,尤其是计算强激波问题时的鲁棒性。 考虑类似于4.1节小扰动分析的二维稳态激波问题,马赫数为7的稳态激波位于x=0.5处,区域[0,1]×[0,0.5]划分成100×50的正方形网格。波前和波后的初始分布为 (25) 左右边界固定为波前和波后状态,上下使用周期性边界条件。从图5可以看出,原始的HLLC格式和文献[25]构造的HLLC+SV格式都出现了明显的不稳定现象,而R-HLLC格式有效地抑制了不稳定现象的发生,表明仅增加剪切粘性不能完全消除HLLC格式的不稳定性。 马赫数为20的正激波沿x-方向传播,波前和波后的初始状态为 (26) 区域[0,1000]×[0,20]划分成步长Δx= Δy= 1的正方形网格。在波前流场的初始分布上添加取值从-0.5×10-6到0.5×10-6的随机扰动。图6 展示了t=40时的密度等值线。可以看出,HLLC格式形成了明显的carbuncle,激波结构完全破坏,而R-HLLC格式展示了清晰的激波面。图7给出了整个区域内y-方向速度最大值随时间的变化情况。HLLC格式计算得到的 max(|v|) 由10-6量级迅速增长到100量级,而R-HLLC格式计算得到的 max(|v|) 一直维持在初始时的10-6量级。 计算高超声速绕柱流问题的稳态解是研究数值格式是否会遭遇致命的carbuncle现象的一个常规测试问题。马赫数为20的高超声速流流经一圆柱体,问题的详细描述参见文献[21]。本文采用40×80的结构化贴体四边形网格。图8展示了t=4时的计算结果。可以看出,HLLC格式的激波面在流场中心线附近出现了轻微的不稳定现象,而本文构造的R-HLLC格式得到了清晰的稳态弓形激波。 图5 二维稳态激波问题的密度等值线 图6 随机数值噪声问题的密度等值线 马赫数为5.09的右行超声速激波绕过一个90°的角,区域[0,1]×[0,1]划分成步长Δx= Δy=1/400的正方形网格,角点位于(0.05,0.625)处。初始条件和边界条件参见文献[11]。图9展示了t= 0.1561时的计算结果。可以看出,HLLC格式出现了明显的激波失稳现象,而R-HLLC格式则完全消除了伪振荡,得到了清晰的激波面。对于次激波、接触面、膨胀波和入射激波两者具有相同的分辨率。 初始时,区域[0,0.25]×[0,1]上下部分两种流体的初始状态为 (27) 图7 y-方向速度的最大取值 图8 高超声速绕柱流问题的密度等值线 图9 激波后台阶绕射问题的密度等值线 图10 Rayleigh-Taylor不稳定性问题的密度等值线 计算复杂的激波/边界层相互作用问题来检验格式的精度。计算区域[0,1]×[0,0.5]划分成步长Δx= Δy= 1/512的均匀网格。初始条件为 (28) 无粘通量的计算采用二阶MUSCL重构,粘性通量的计算采用二阶中心差分,时间离散采用二阶 Runge -Kutta 格式。计算中,雷诺数取220。从 图11 可以看出,R-HLLC和HLLC格式得到了几乎相同的解。图12表明,两种格式的计算结果沿着底部壁面的密度分布完全吻合。该算例证明了R-HLLC格式在计算粘性流问题时的有效性。 图11 激波/边界层相互作用问题的密度等值线 图12 底部壁面的密度分布 构造了一种激波稳定的HLLC格式。稳定性分析表明,HLLC格式横向通量的密度与剪切速度的扰动不会发生衰减。在横向数值通量上增加熵波与剪切波粘性来抑制激波不稳定现象的发生。为了保留HLLC格式低耗散性的优点,定义开关函数来自动控制添加粘性的位置和大小。新的格式实施简单,仅需在现有HLLC程序的基础上增加若干行代码,并且不会引入依赖于问题的可调参数。数值算例的计算结果展示了新的HLLC格式具有高分辨率和强鲁棒性的优点。此外,构造其他鲁棒的Godunov型激波捕捉格式、开发三维和非结构网格上的R-HLLC格式,并将其应用到其他的高超声速复杂流动问题的数值模拟值得进一步研究。
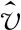
4.2 横向数值通量与不稳定性之间的关系
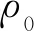
5 一种鲁棒的HLLC格式
5.1 开关函数
5.2 R-HLLC格式
6 数值实验
6.1 二维稳态激波问题

6.2 随机数值噪声问题
6.3 高超声速绕柱流问题
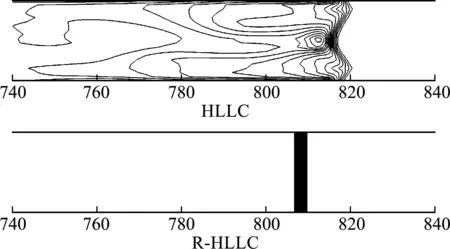
6.4 激波后台阶绕射问题
6.5 Rayleigh-Taylor不稳定性问题
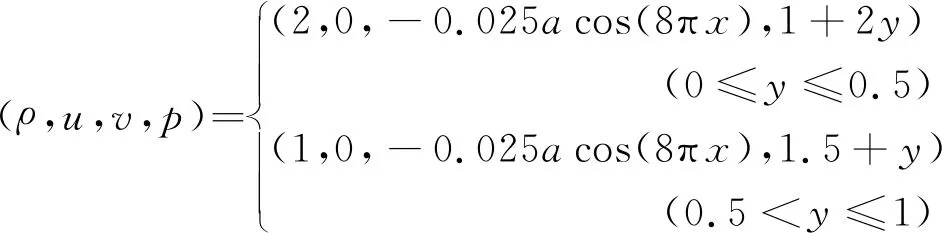


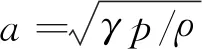
6.6 激波/边界层相互作用问题


7 结 论
