黏弹夹芯板的有限元建模及实验研究
2020-12-23黄志诚王兴国吴南星褚福磊
黄志诚, 王兴国, 吴南星, 褚福磊, 罗 经
(1.景德镇陶瓷大学 机械电子工程学院,景德镇 333403; 2.清华大学 机械工程系,北京 100084;3.北京机械工业自动化研究所有限公司,北京 100084)
1 引 言
对于各种车辆、飞机和船舶等,其内外部噪声和振动水平是最重要的设计标准之一[1]。同时,这些领域经常要求控制产品的重量,需要大量使用薄壁件,而因其轻薄的特性,在激励下更容易产生振动和噪声。在飞机和一些高端汽车中,振动主动控制是满足技术需求的一种方式,但代价是成本较高[2]。所以,更常见的是在结构中添加被动阻尼材料以降低噪音和振动水平。其中,被动约束层阻尼PCLD(Passive constrained layer damping)形式的应用阻尼材料在降低结构振动能量方面非常有效[3]。图1所示的黏弹夹芯板结构即为一典型的PCLD板结构。其技术原理是高损耗因子黏弹性材料层(如橡胶)附着在基板结构上,并且在其另一侧受到刚性层(如金属)的约束(约束层)。 因此,当基板产生弯曲振动时,黏弹性层将经受大的剪切变形,使动能转化为热能耗散掉,达到减振降噪目的。这种结构在没有显著改变构件重量的情况下能够有效地抑制振动,所以在对重量有严格限制的场合应用广泛。其动力学建模和振动及阻尼特性一直是研究的热点问题。
本文基于经典板理论对黏弹夹芯板结构进行了有限元建模,采用Biot模型描述黏弹性材料参数的频率依赖特性并给出了识别其参数的方法。通过引入辅助坐标将Biot模型和黏弹夹芯板的有限元方程相结合,并将其转化成便于求解的标准二阶定常线性系统方程形式。最后,对黏弹夹芯板的振动特性进行了分析和实验研究,结果表明本文方法是正确可靠的,对同类工程振动问题的解决有一定参考应用价值。

图1 黏弹夹芯板结构
2 有限元建模
2.1 基本假设
假设黏弹夹芯板的两个弹性层(基板和约束层)的剪应变忽略不计,只考虑中间黏弹性层的剪应变;各层沿厚度方向的挠度变化可忽略,即三层具有相同的挠度,中面只发生弯曲变形;弹性层不耗散振动能量,黏弹性层为不可压缩材料,通过剪切变形耗散能量;黏弹性层为线性黏弹性材料,其本构模型由复剪切模量模型表示;各层结合面完美粘合,不存在相对滑动。
2.2 运动学关系
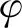
基于上述假设和图2所示的运动关系,可得黏弹性层x向和y向位移分别为[14]
(1)
(2)
黏弹性层绕y轴和x轴的剪应变分别为
(3)
(4)
式中d= (h3+h1)/2+h2为约束层和基板中面间的距离。
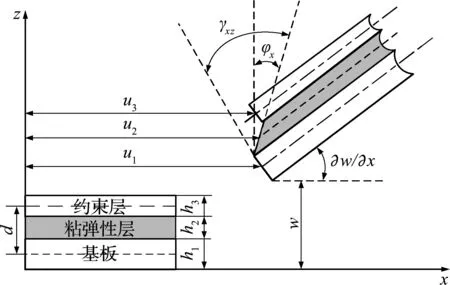
图2 xoz截面黏弹夹芯板的运动关系
2.3 自由度与形函数
构造如图3所示的夹芯板单元。该单元为四节点矩形单元,尺寸为2a×2b。每个节点有7个自由度,分别为板单元基板层和约束层面内x向和y向位移u1,v1,u3和v3、板的横向位移w及绕x轴和y轴的转角θx和θy。其空间分布函数(插值函数)为
u3=a1+a2x+a3y+a4xy
v3=a5+a6x+a7y+a8xy
u1=a9+a10x+a11y+a12xy
v1=a13+a14x+a15y+a16xy
w=a17+a18x+a19y+a20x2+
a21xy+a22y2+a23x3+a24x2y+
a25xy2+a26y3+a27x3y+a28xy3
θx= ∂w/∂y,θy=-∂w/∂x
(5)
式中系数a1,a2,…,a28由单元4个节点的28个节点位移向量Δe来决定。节点位移向量为
(6)
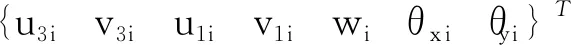
(i= 1,2,3,4)(7)
因此,单元内任意位置(x,y)的位移Δ可由单元节点位移矢量插值得到,即
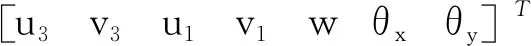
(8)

将形函数N代入式(1~4),可得对应于黏弹性层纵向位移u2,v2和剪应变γx z,γy z的形函数分别为
(9)
(10)
(11)
(12)
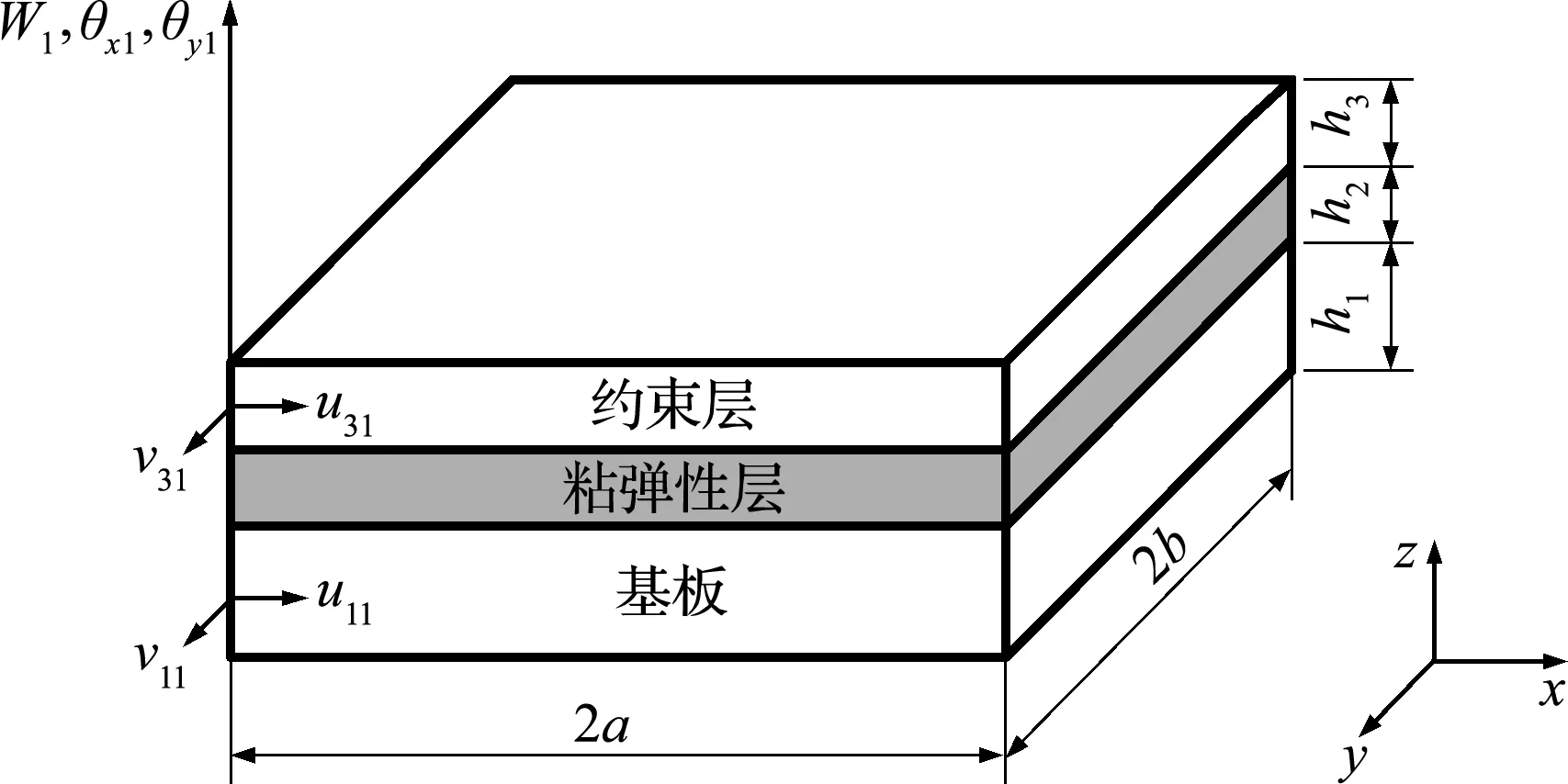
图3 28自由度板单元示意图
2.4 单元运动方程
2.4.1 势能
根据经典板理论[15]可得单元不同层因拉伸和弯曲引起的势能为
(13)
式中下标i(i= 1,2,3)分别表示该参数属于基板、黏弹性层和约束层,
(14)
为第i(i= 1,2,3)层面内弹性矩阵,其中Ei和νi分别为第i层的弹性模量和泊松比,
(15)
为第i层的弯曲弹性矩阵,ke i和kb i分别为第i层与拉伸和弯曲相关的刚度矩阵,其表达式为
(16)
式中Be i和Bb i(i= 1,2,3)分别为基板、黏弹性层和约束层的拉伸和弯曲应变-位移矩阵,其表达式分别为
(17)
黏弹性层的剪切应变能为
(18)
式中G为黏弹性材料的剪切刚度矩阵,其表达式为
(19)
式中Gx为x向剪切模量,Gy为y向剪切模量。本文研究的黏弹性材料为各向同性材料,所以有Gx=Gy=Gv,其中Gv为黏弹性层的剪切模量,一般情况下为复数形式。ks v为黏弹性层的剪切刚度矩阵,其表达式为
(20)
式中Bs v为黏弹性层的剪应变矩阵,其表达式为
(21)
显然,单元总势能为各层势能之和
(22)
则单元总刚度阵为各层刚度阵之和
(23)
式(23)可简写为
ke=ke+ks v
(24)
式中ke为单元的弹性刚度阵,其表达式为
(25,26)
式中G=Gv为黏弹性材料的剪切弹性模量,kv v为单元粘性刚度阵,其表达式为
(27)
2.4.2 动能
板单元各层动能也包含拉伸和弯曲动能两部分。第i层(i= 1,2,3)的动能为
(28)

单元总动能为各层动能之和,即
(29)
应用形函数,则可得单元总质量阵
(30)
式中me i和mb i分别为第i层拉伸和弯曲质量阵。这些质量阵的表达式分别为
(31)
2.4.3 单元运动方程
将单元势能及单元动能代入哈密尔顿(Hamilton)原理的变分形式可以推导出单元运动方程
(32)
式中Re为单元外部激励力。
2.5 应用Biot模型
黏弹材料拉氏域的切变模量函数可用Biot模型[16]表示
(33)
式中G∞为黏弹材料剪切模量的平衡(稳态)值,N为微振子系列项数,{ak,bk}为正常数。如果取N阶微振子,该模型有2N+1个参数需要确定。这些参数可以通过对实验数据进行曲线拟合得到。
将单元运动方程(32)进行拉氏变换得
(34)
将Biot模型的表达式(33)代入式(34)并引入辅助耗散坐标
(35)
式中k= 1,2,3,…,N。经整理后可得到单元动力学方程为
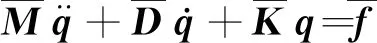
(36)
式中
(37)
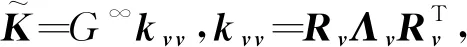
显然式(36)为普通的二阶定常线性系统动力学方程,求解固有频率和阻尼等模态参数都很直接方便,这一优点使得Biot模型具有很好的工程应用价值。
3 数值模拟
考虑三根长度不同但其他参数相同的悬臂黏弹夹芯板结构,其几何和材料参数列入表1。文献[17]对这三种不同的悬臂板进行了一系列实验以确定黏弹材料的机械性能参数。本节将应用本文板单元分别对这三种不同的悬臂板进行分析,得到其前三阶固有频率和损耗因子,将所得结果与实验值进行对比以验证本文模型。
表1中黏弹材料的弹性模量实部和损耗因子随频率变化而变化,文献[17]通过实验确定其表达式分别为
(38)

(39)
式中α=5.26 MPa,β=55.59×106s-1
δ=6.98×109s-2,ε=0.58 MPa
式(38,39)通过数学变形得到形如取两阶微振子项的Biot模型表达式,其参数可以直接提取,列入表2。
应用本模型分别计算该板前三阶固有频率和损耗因子值,并与实验值对比,结果列入表3。计算时,该板沿长宽方向离散成50×40个单元。

表1 悬臂黏弹夹芯板的几何和材料参数

表2 黏弹材料Biot模型参数
由表3可知,在对固有频率的预估中,本文模型对三根板的预估误差都在3%以下,最低误差为1.5%,最高误差为2.78%,平均误差为2.13%。在对结构损耗因子预估中,本文模型的预估误差都在5%以下,最低误差为2.32%,最高误差为4.58%,平均误差为3.25%。上述结果表明,本文方法是准确有效的。
4 实验研究
为进一步验证本文推导的有限元板模型,对一黏弹夹芯板进行自由振动测试实验。该板的边界条件为一边固支,另三边自由。长为290 mm,宽为80 mm,其约束层、黏弹性层和基板厚度分别为1.0 mm,0.5 mm和1.7 mm。其材料参数列入表4。
核心层材料选用国产 Z N -1 型黏弹性材料,文献[18]测得其在不同激励频率下的储能模量和损耗因子值,据此通过曲线拟合得到其Biot模型参数,列入表5。
通过如图4所示的实验装置测得黏弹夹芯板前三阶固有频率,对应的损耗因子由半功率法得到,然后使用本文推导的有限元模型来计算板的固有频率和损耗因子。计算时,板沿长宽方向划分为20×8个单元。前三阶固有频率和损耗因子的实验和计算结果列入表6。

图4 结构模态实验
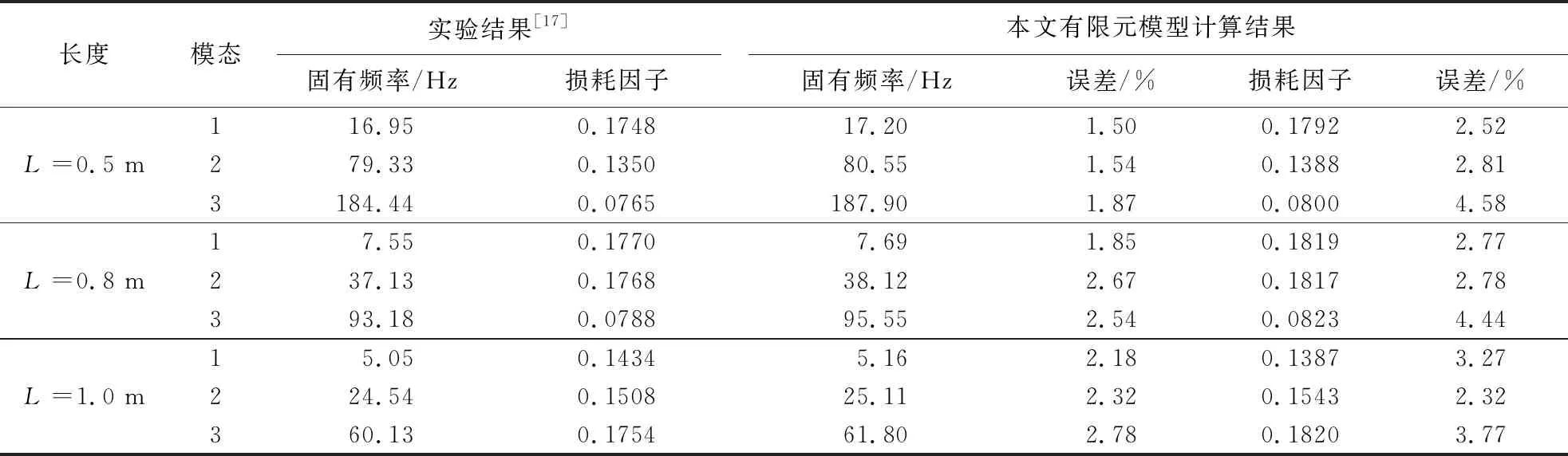
表3 不同长度的黏弹夹芯板前三阶固有频率和损耗因子的实验值和数值模拟结果对比Tab.3 Comparison of experimental values and numerical simulation results of first three natural frequencies and loss factors of viscoelastic sandwich plates of different lengths

表4 黏弹夹芯板结构的材料和几何参数

表5 Z N -1型黏弹材料Biot模型参数

表6 悬臂黏弹夹芯板前三阶固有频率和损耗因子的计算和实验结果比较Tab.6 Comparison between calculation and experimental results of first three natural frequencies and loss factors of cantilever viscoelastic sandwich plate
由表6可知,本文有限元模型的计算结果与实验结果吻合良好,这说明黏弹性材料Biot模型能够很好地描述黏弹性材料参数随频率变化的特性,本文黏弹夹芯板有限元模型是准确有效的。
5 结 论
建立了黏弹夹芯板的有限元动力学模型。采用黏弹性材料Biot模型描述其力学性能参数的频率依赖特性,通过引入辅助坐标将其与三层四节点28自由度板单元结合,将黏弹夹芯板的有限元动力学方程改造成二阶线性系统形式,降低了常规非线性系统方程的求解难度。通过数值模拟和实验研究验证了本文方法的有效性。
