基于BP神经网络的无刷直流电机控制系统

2020-12-23黄亮程

机电信息 2020年32期

张闯王勋黄亮程

（贵州电网有限责任公司贵阳供电局，贵州贵阳550008）

0 引言

无刷直流电机可以根据判断转子所在位置信息，通过电力电子元器件来实现换向，克服了普通直流电机通过机械换向器实现换向存在的诸多缺点，因而被广泛应用于诸多领域[1]。传统PID控制方法仅适用于线性系统，且控制精度不高，而无刷直流电机（BLDCM）采用电子换向方式[2]，是具有强耦合、变量多等优点的非线性系统。传统PID控制方法已不能满足高精度、高性能的控制要求，智能控制[3]及新型控制算法[4]成为研究的主流。因此，在传统PID控制方法的基础上，引入智能化控制方法对提高系统整体性能具有重要意义。本文对设计的两种控制器进行了仿真实验，以证明所设计的控制器的有效性。

1 无刷直流电机基本工作原理

无刷直流电机主要由电机本体、位置检测装置、电子换向装置以及驱动控制器构成。电机运行过程中需要控制电机速度，在无刷直流电机速度控制中，电机通过传感器装置对转子位置信号进行检测，得到转子的位置信息，再根据所获得的信息，驱动控制器控制电子换向装置中电力电子器件的关断，以达到换向的目的，从而保证电机稳定运行。

三相绕组为星形连接，其电压平衡方程为：

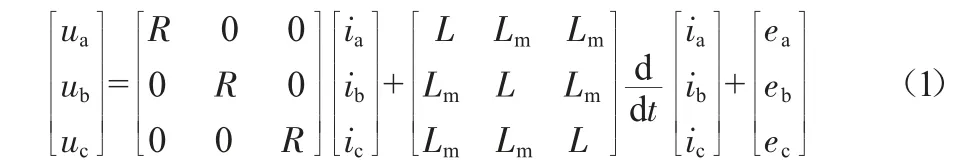
式中：ua、ub、uc为电机绕组相电压；ea、eb、ec为电机绕组电动势；ia、ib、ic为电机绕组相电流；L、Lm分别为电机绕组的自感和定子每两相绕组之间产生的互感；R为电机绕组电阻。

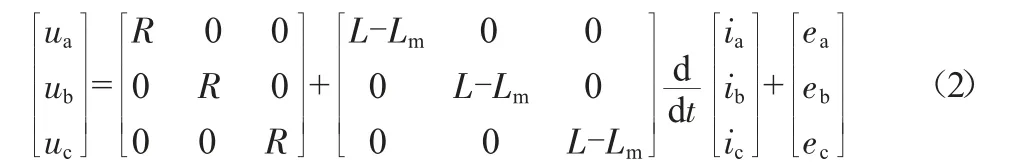
电机的电磁转矩为：

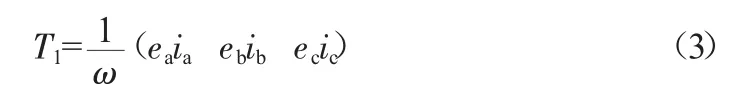
电机运动方程：

式中：T1为电磁转矩（Nm）；T2为负载转矩（Nm）；J为转子惯性矩（Nm）；ω为机械角速度（rad/s）。

2 PID控制

PID控制方法是将反馈所得到的误差信号进行比例、积分以及微分运算结果叠加，从而获得输出信号。在实际应用中，多是通过人工试凑法来确定PID的参数Kp、Ki、Kd，其中，Kp为比例时间常数，Ki为积分系数，Kd为微分系数。常规PID控制系统仿真模型如图1所示。

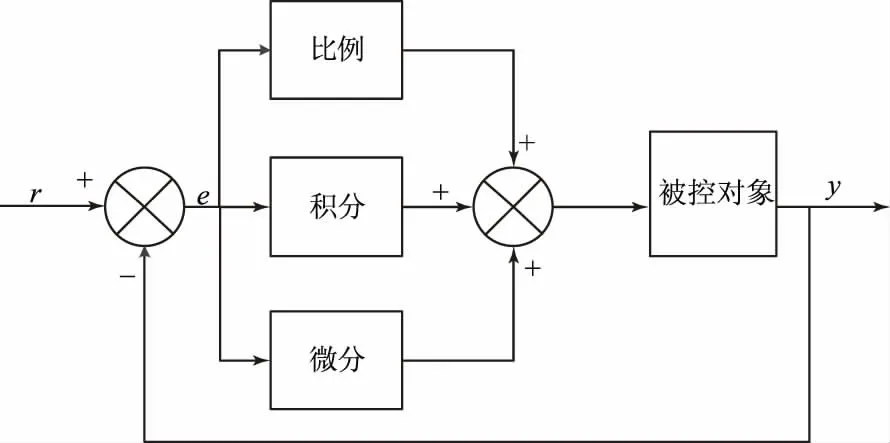
图1 常规PID控制系统仿真模型

3 BP神经网络

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最为广泛的神经网络。其基本思想是梯度下降法，即利用梯度搜索技术，使网络的实际输出与期望输出误差均方根最小。BP神经网络结构为输入层得到信号后将其传给隐藏层，隐藏层则根据神经元相互联系的权重、规则把这个信号传给输出层。输出层负责对比结果，如果结果不正确，则根据误差，返回并调整神经元相互联系的权值。通过信号的正向和反向传播过程对各层的权值不断进行调整，从而使预测结果不断逼近期望结果，该过程也称为神经网络的训练过程，如图2所示。

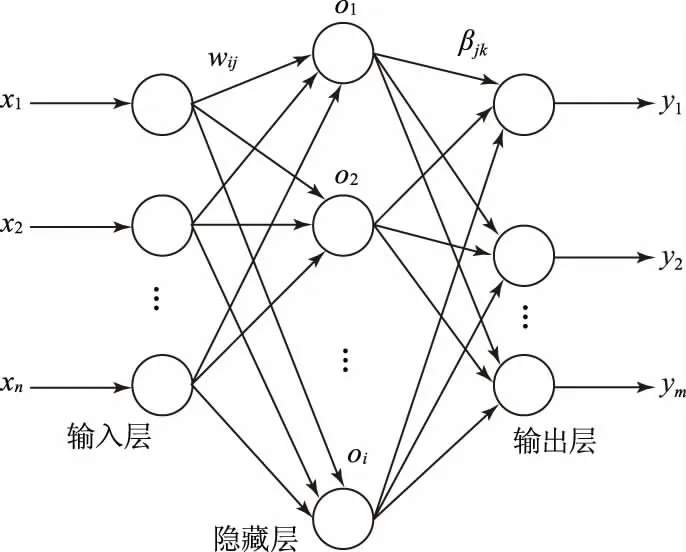
图2 神经网络的训练过程

4 基于BP神经网络的PID控制原理

BP神经网络通过不断学习样本来优化和修正神经元相互联系的权值，逐步获得样本数据输入与输出的映射关系。BP神经网络的精度较高，将其应用于传统PID控制中可获得较为精确的控制参数，以实现最佳的PID控制。利用BP神经网络对PID控制器的3个参数Kp、Ki、Kd进行在线调节，使用BP神经网络可以设计参数Kp、Ki、Kd自学习的PID控制器，如图3所示。

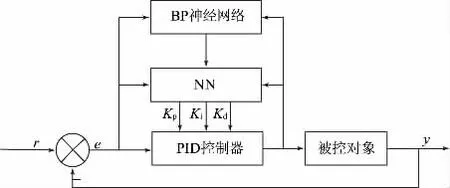
图3 基于BP神经网络的PID控制器结构

5 实验仿真分析

在PID控制算法技术上引入BP神经网络对电机转速进行测试，其中BP神经网络结构为输入层3个节点，隐含层6个节点，输出层为3个节点，学习速率为0.24，惯性系数为0.03，误差精度设置为0.000 01。初始时刻，BP神经网络输入层到隐含层链的接权值在（-1，1）随机产生。将设定值与无刷直流电机实际输出值的差值序列作为神经网络的训练数据，对神经网络进行训练，从而获得最优的参数Kp、Ki、Kd值。本实验从响应时间及鲁棒性两方面来验证基于BP神经网络的PID控制模型较传统PID控制模型，针对直流无刷电机的控制性能优越。

无刷直流电机控制系统空载启动，进入稳态过程，电机转速波形仿真结果如图4所示，基于BP神经网络的PID控制模型在0.45 ms达到稳定，而传统PID控制模型在1.13 ms达到稳定，由此可见，通过引入BP神经网络，PID控制对参数整定速度明显变快。

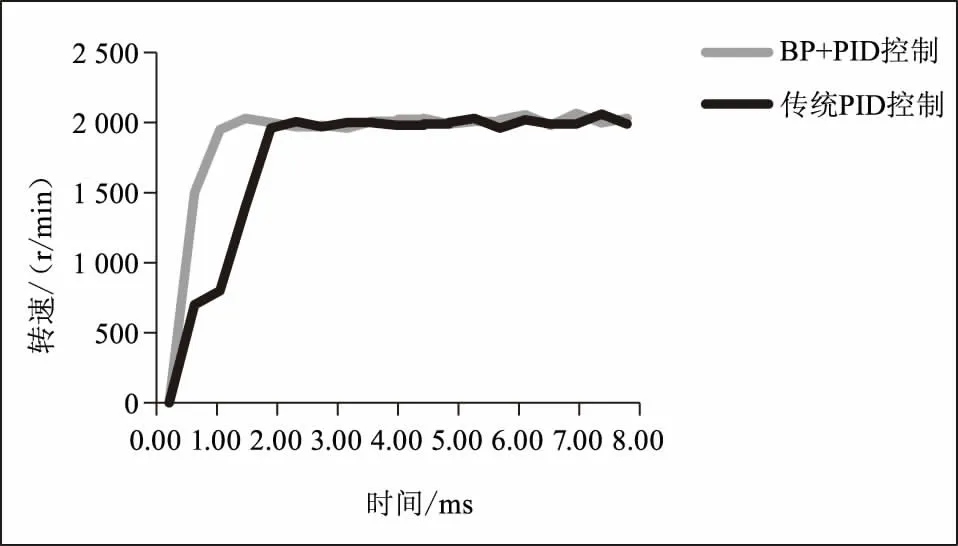
图4 给定转速下电机转速波形仿真结果

通过对电机转速进行突变调整，观察传统PID控制模型与基于BP神经网络的PID控制模型的响应时间。在1.60 ms时，将电机转速由2 000 r/min突然调整至1 500 r/min，在3.4 ms时，又突然恢复至2 000 r/min。转速突变下鲁棒性对比曲线如图5所示，在两个转速突变的节点，基于BP神经网络的PID控制模型于1.74 ms和4.26 ms达到稳定，而传统PID控制模型则分别在1.93 ms和4.47 ms回到稳定状态，由此可见，基于BP神经网络的PID控制模型能够快速调整参数，使转速恢复稳定，鲁棒性更强。