中美规范下缓和曲线最小长度对比分析

曾志刚 杜朝阳

(中交第二公路勘察设计研究院有限公司 武汉 436000)

近年来随着我国“一带一路”重大战略的全面推进，越来越多的中国设计、施工等工程单位进军海外市场，在项目推进过程中不可避免地需要理解和应用国外特别是欧美规范，美国采用《A Policy on Geometric Design of Highways and Streets 》[1](以下简称《美国规范》)作为指导公路与城市道路设计的规范，在美洲地区被广泛应用。

本文结合牙买加南部沿海高速公路项目的设计实例，对中、美两国规范中对高速公路缓和曲线最小长度Ls的最小值设定加以研究。

1 缓和曲线

在平曲线上，当汽车从直线进入圆曲线时，驾驶员应当逐渐转动方向盘，以改变前轮的转向角，使其适应相应的圆曲线。前轮的逐渐转向是在进入圆曲线之前的某一段内完成的，这一曲率不断变化的路段就是缓和曲线段。缓和曲线的设置具有以下3个方面的作用[2]。

1) 缓和曲线曲率的逐渐变化，便于驾驶员在缓和曲线上的驾驶操作，使汽车能安全舒适地进入圆曲线。

2) 直线和圆曲线间设置缓和曲线后，汽车行驶过程中从没有离心力的直线段进入到有离心力的圆曲线段，即缓和曲线消除了离心力的突变。

3) 当需要设计超高和加宽时，可在缓和曲线内完成超高和加宽的渐变。

2 缓和曲线最小长度

2.1 按线形曲率过渡要求计算

在高速行驶或曲率急变时，汽车可能超越当前车道驶出一条很长的过渡性轨迹线。从安全角度出发，有必要设置一条驾驶员易于遵循的路线，使车辆在进入或离开圆曲线时避免因曲率骤变侵入其他车道，这就决定缓和曲线必须保证一定的长度，以避免车辆在回旋线上行驶时间过短而使驾驶者操纵过于匆忙。假定汽车行驶速度为v(km/h),汽车在缓和曲线上行驶的最小时间为t(s)，则缓和曲线最小长度Ls1的计算方法见式(1)。

(1)

我国习惯认为汽车在缓和曲线上的行驶时间至少应有3 s，则Lsmin1的计算方法见式(2)。

(2)

JTG D20-2017 《公路路线设计规范》[3](以下简称《中国规范》)就是按3 s行程制定了各级公路缓和曲线的最小长度指标，并向上修正成最小5 m间隔的整数，见表1。

表1 《中国规范》中缓和曲线最小长度

《美国规范》认为汽车在缓和曲线上的行驶时间至少应有2 s，即Lsmin2的计算方法见式(3)。

(3)

《美国规范》按2 s行程制定了各级公路缓和曲线的最小长度指标，并且近似取整，取值见表2。

表2 《美国规范》中缓和曲线最小长度

2.2 根据超高渐变率计算

行车道从直线上的双坡断面过渡到圆曲线上的单坡断面，一般是在回旋线长度内完成的。如果回旋线过短，超高渐变率过大，则会因路面急剧地由双坡变为单坡而使路面扭曲，对行车和路容均不利，如果超高渐变率过小，则对排水不利，因此，对由于超高过渡而引起的路面旋转角速度应控制在不使人感到不舒适的程度。

《中国规范》中规定了适中的超高渐变率，由此可推导出计算超高缓和段最小长度的计算方法见式(4)。

Ls min3=B×Δi/P

(4)

式中：B为超高旋转轴至硬路肩外边缘的宽度，m；Δi为设计超高坡度与路拱坡度的代数差，%；P为超高渐变率，%，见表3。

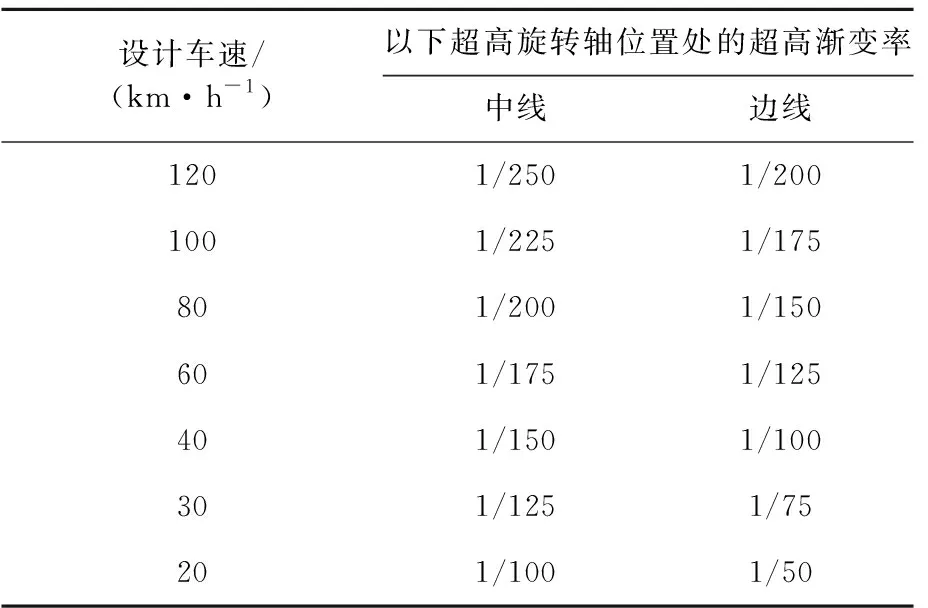
表3 《中国规范》超高渐变率

虽然设置缓和曲线能使路线和离心力的变化均处于一个渐变的过程，但是目前缺少确切的数据证实缓和曲线对于车辆在道路上行驶是必不可少的，因此《美国规范》并未要求平曲线设计时必须使用缓和曲线。由直线直接过渡到圆曲线的设计中，《美国规范》对超高缓和段的最小长度作了如式(5)所示要求，设计中可以参考用于确定缓和曲线长度。

式中：w为单条行车道的宽度，m；n1为旋转的行车道数；ed为设计超高坡度，%；bw为行车道数的调整系数，见表4;Δ为超高渐变率，%，见表5。

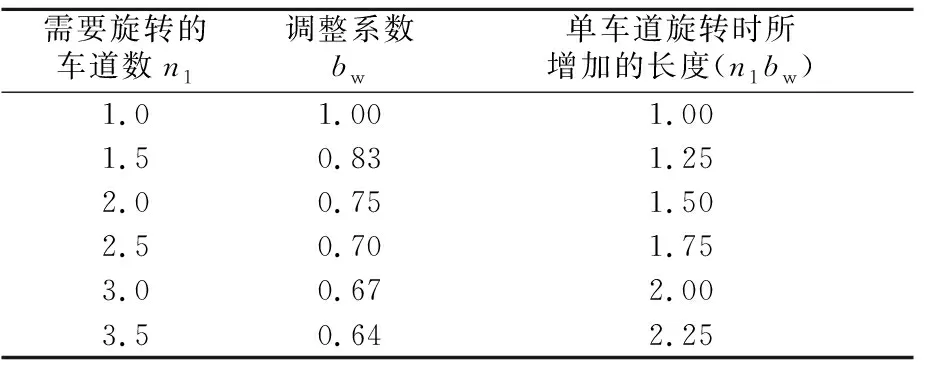
表4 《美国规范》中不同旋转车道数的调整系数

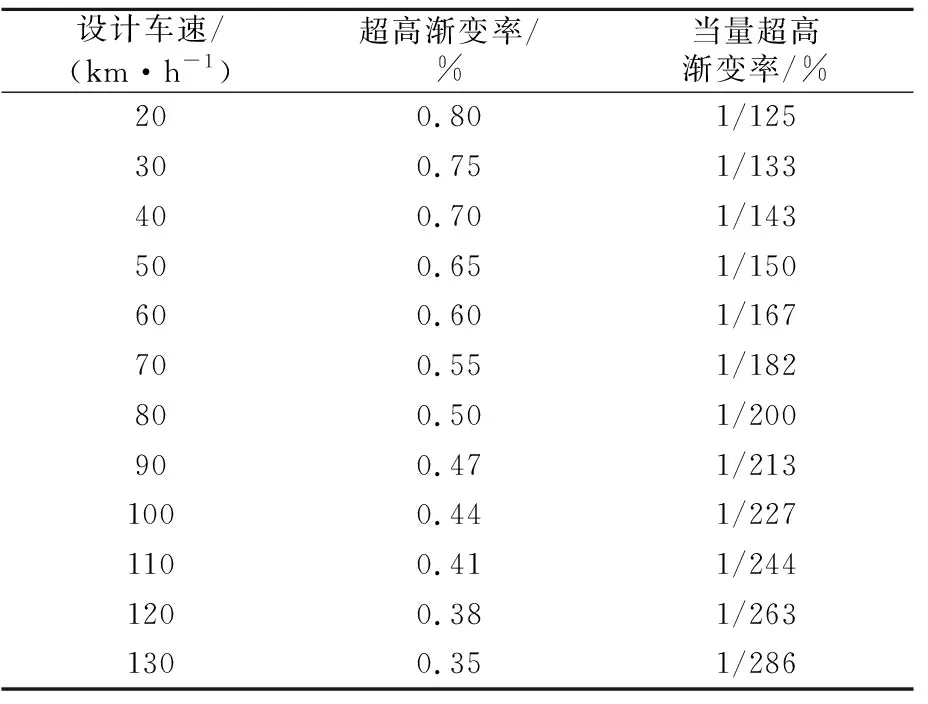
表5 《美国规范》超高渐变率

2.3 考虑乘客的舒适度要求

汽车行驶在回旋线上，其离心加速度将随回旋线曲率的变化而变化。若变化过快，将会使乘客有不适感。为使乘客感觉舒适，回旋线需要有一定的长度保证。

则

(6)

因此，选定能保证舒适度的最大离心加速度变化率αt就能得出在车速v(km/h)和圆曲线半径R条件下的最小缓和曲线长度。对于离心加速度变化率αt我国公路上一般控制在0.5～0.6 m/s3之间[4]，等级高的公路取低值。于是缓和曲线最小长度的计算方法见式(7)。

(7)

对于高速公路,当速度增加时，空气动力及其他动力作用会影响车辆尤其是大型半挂车在曲线上的行驶轨迹,因此其横向加速度变化率可减小为0.45 m/s3，据此计算的回旋线长度也应相应地增长，其取值见表6。

表6 高速公路缓和曲线最小长度建议值

美国公路设计中离心加速度变化率通常采用0.3～0.9 m/s3，同时还要考虑超高的影响加以修正，最大值推荐采用1.2 m/s3。于是缓和曲线最小长度计算方法见式(8)。

(8)

2.4 根据车辆最小侧向偏移计算

《美国规范》中强调，缓和曲线需要有足够的长度使车辆在正常的轨迹下行驶，其侧向偏移量不会超出自己的行车道。根据这个标准确定出的缓和曲线的最小长度计算方法见式(9)。

(9)

式中：Pmin为车辆在直线与圆曲线之间的缓和曲线上的最小侧移量，中、美两国规范推荐值均为行驶力学上要求的0.2 m；Pmin为圆曲线半径，m。

2.5 考虑线形顺适及美观要求

以上4种决定缓和曲线长度取值的因素都是从行车安全性、舒适性方面考虑，中国规范还从线形顺适美观角度推荐了缓和曲线长度的取值。考虑驾驶员的视觉，缓和曲线的旋转角在3°左右时，曲线极不明显，在视觉上容易被忽略，旋转角大于29°时，圆曲线与缓和曲线不能很好协调，因此最适宜的旋转角为3°～29°。

旋转角为

则

因此缓和曲线满足视觉需求且使线形圆顺的条件是其参数A按R/3≤A≤R取值，根据回旋线公式Ls=A2/R可得R/9≤Ls≤R。

3 实例分析

现以牙买加东西高速项目山区段为实例，分析AASHTO规范下缓和曲线长度的取值。项目设计速度为80 km/h，标准路幅25.2 m(1.0 m土路肩+2.5 m右侧硬路肩+7.3 m行车道+1.5 m 左侧硬路肩+0.6 m中央分隔带+1.5 m左侧硬路肩+7.3 m行车道+2.5 m右侧硬路肩+1.0 m土路肩)，路拱横坡为2.5%，土路肩横坡为4.0%。某一圆曲线半径为400 m，超高取值为6.6%，根据AASHTO规范进行缓和曲线长度计算。

按线形曲率过渡要求计算

根据超高渐变率计算

w=3.65，n1=(2.5+7.3+1.5)/3.65≈3，

ed=6.6，bw=0.67，Δ=0.5

则有

考虑乘客的舒适度要求计算

根据最小侧向偏移计算

综上，向上取整Ls min=100 m。

分别采用《美国规范》及《中国规范》计算本项目山区段不同半径的圆曲线对应的缓和曲线最小长度取值。绘制中、美规范下缓和曲线长度最小值对比曲线见图1。

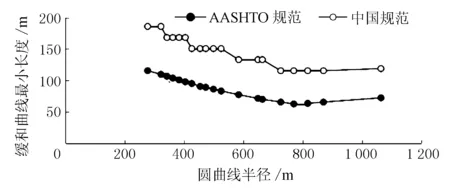
图1 中美规范下缓和曲线长度最小值对比曲线

由图1可见，中美两国缓和曲线最小长度均由超高渐变率决定。显然，《中国规范》计算的缓和曲线最小长度大于《美国规范》计算的缓和曲线最小长度。主要原因分析如下。

1) 《中国规范》规定：超高过渡宜在回旋线全长范围内进行。因此根据最大超高变化率来计算最小缓和曲线长度时，采用的是设计超高与路拱横坡的代数差来进行计算。《美国规范》中超高过渡由直线缓和段和超高缓和段组成，直线缓和段曲线外侧横坡由正常路拱渐变至零坡，超高缓和段由零坡渐变至全超高。因此计算最小缓和曲线长度时，横坡差值即为设计超高值。

2) 《美国规范》计算超高缓和段长度对不同旋转车道数有不同的调整系数，车道数越多系数越小。

4 结语

经过对中、美两国缓和曲线最小长度取值的对比分析，可以发现两国规范在设计理念、参数选值上的不同。美国超高缓和段的设置与中国有较大不同，设置起点位于直线段，导致需要设置的缓和曲线长度相对中国较小。在以美国规范为主的项目设计中，设计者应该从项目特点出发，考虑安全、视觉、景观等角度，选用合适的缓和曲线最小长度，从而设计出安全、经济、舒适、和谐的平面线形。