三维集成微系统散热微通道均温性研究

唐清林，兰 欣，李祥瑞

(山东大学 能源与动力工程学院，山东 济南 250061)

0 引言

高换热效率的液冷式微通道换热技术，虽然已成为解决高功率芯片散热问题的重要手段[1-2]，但其壁面温度梯度过大将导致微系统可靠性降低[3]。在高功率密度下，由于三维微系统内各叠层材料热膨胀系数存在差异，较大壁面温升会在不同材料界面产生热-机械应力，严重影响系统可靠性。此外，由于芯片内部介电层、铜互连及芯片基底材料物理特性有差异，较大温度梯度会在不同尺度材料界面上产生随循环功率变化的热应力，由此产生不可忽略的热-机械可靠性问题，甚至会导致芯片乃至三维微系统最终失效。因此，减小散热面过高的壁面温升和过大的温度梯度是保障系统可靠性的必要条件。

为提高微通道壁面均温性，文献[4]通过试验研究单层直微通道，发现水力直径越小，壁温标准差越低。文献[5]通过试验与模拟分析铜基蛇形通道，发现单蛇形通道比矩形直通道换热性能高35%，但压降及壁面温度梯度过大。文献[6]设计了V型肋，使蛇形通道进出口压降减小60%，且提高了壁面均温性。文献[7]通过试验和模拟研究双层硅基微通道，发现在不同流率下顺流结构壁面温升更低，逆流结构壁温分布更均匀。文献[8]通过模拟研究双层互异结构微通道，发现双层异构比双层同构壁温更均匀。为避免顶层出口侧高温流体对底层入口侧低温流体的热效应，文献[9]通过模拟研究顶层截断式双层微通道，提出顶层最优无量纲截断距离为0.38。文献[10]提出变密度肋微通道结构，使壁面温度变化小于2 ℃/mm。文献[11]研究了交错布置变密度肋结构，同平行变密度肋相比，交错肋降低系统热阻，提高系统整体均温性，但压降损失增加。文献[12-14]通过试验和模拟研究铜、硅基斜截式微通道，发现斜截结构压降较小且换热能力较强。文献[15]通过模拟研究含扰流肋的斜截式微通道，发现含肋斜截结构换热能力更强，但压降损失更大。

综上，大量研究通过设计、优化结构提高微通道换热性能和均温性，其中，压降较小的斜截结构和换热较强的含肋斜截结构仍存在壁面温度梯度较大的问题。为提高微通道换热性能，同时保证壁温均匀性，本文对微通道进行结构设计。探究不同入口流速Vin=0.3～0.7 m/s时，通道结构分别为矩形微通道热沉(rectangular microchannel heat sink，R-MCHS)、斜截式微通道热沉(oblique microchannel heat sink，O-MCHS)、含肋斜截式微通道热沉(oblique and ribbed microchannel heat sink，OR-MCHS)和混合式微通道热沉(hybrid microchannels heat sink，H-MCHS)的均温特性。出口侧采用强换热能力含肋斜截结构及增加入口流速均可显著提高壁温均匀性。本文研究可为三维集成微系统散热及可靠性设计提供参考。

图1 4种微通道的几何结构图

1 模型设计

1.1 物理模型

本文研究的铜基微通道模型由10个平行直通道组成。在不考虑微通道边缘效应的情况下，将通道模型进行简化。选择微通道散热器的1个周期对称几何结构进行分析。图1展示了4种微通道的几何结构。H-MCHS前半段采用斜截结构，后半段采用含有扰流肋的斜截结构。主通道宽度Wm为0.5 mm，肋的宽度Wf为0.5 mm，通道长度Lc为25 mm，通道高度Hc为1.5 mm，基板厚度Hb为0.3 mm。

1.2 数值模型

为分析微通道模型的散热特性，使用fluent软件进行流固耦合计算。并做如下假设：微通道中冷却介质为不可压缩流体；流动与传热过程是在稳态条件下进行的；忽略重力、流体黏性耗散及散热器表面与外界环境间换热。根据上述假设，连续性方程(1)、动量方程(2)、能量方程(3)和能量方程(4)如下：

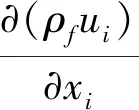
(1)

(2)

(3)

(4)

其中:式(3)和式(4)分别为流体域与固体域的能量方程；ui、uj(i≠j)为x、y、z方向速度,m/s;ρf为流体密度,kg/m3;μf为流体动力黏度，(N·s)/m2;Tf为流体温度,K;cf为流体比热容,(J·kg)/K;kf为流体导热系数,W/(m·K);ks为固体导热系数,W/(m·K);Ts为固体温度,K。

1.3 边界条件的设置

将入口设置为充分发展的速度入口，平均入口流速为Vin，流体温度Tf,in为293.15 K；出口设置为压力出口。在散热器底面施加恒定、均匀的热流密度q=65 W/cm2，周期结构左、右两面设置为周期性边界条件。冷却介质为水，微通道材料为铜，物性参数采用文献[13]的变物性参数设置，比热、运动黏度、流体导热系数及密度均为通道进出口平均温度的函数。采用Simple算法进行压力与速度耦合，速度残差、能量残差分别设置为1×10-6和1×10-8。对计算模型进行网格无关性检验。以H-MCHS为例，对比不同网格密度下H-MCHS最大壁温和进出口压降，发现当网格数量为191.8×104时，最大壁温偏差及进出口压降偏差分别为0.04%和0.57%，因此，采用该密度网格进行后续计算较为合理。

1.4 参数定义

本文中通道水力直径Dh及平均对流换热系数have由式(5)和式(6)计算。为表征壁温分布情况，定义壁温温差Td,w，如式(7)所示。雷诺数Re和平均努塞尔数Nuave由式(8)和式(9)计算。f为范宁摩擦因数，如式(10)所示。η、σ分别为通道强化传热因子和壁温标准差，通过式(11)和式(12)计算。

(5)

(6)

Td,w=Tmax,w-Tmin,w；

(7)

(8)

(9)

(10)

(11)

(12)

其中：q为芯片热流密度；Ah、Acon分别为通道加热壁面面积和流固换热面积；△T为通道壁面平均温度与流体平均温度差值；Tmax,w和Tmin,w分别为壁温最大值和最小值；△p为通道内的压降损耗；Ti,w及Tave,w分别为壁温和壁温平均值。

2 结果与分析

2.1 模型验证

为验证本文数值方法的准确性，与Lee模型[12-13]的数值和实验结果进行对比验证，见图2。图2a为本文壁温分布数值结果与Lee模型壁温数值结果，其最大偏差小于0.1%。图2b为本文进出口压差数值结果与Lee模型实验结果，其最大偏差为8.45%。本文模型数值结果与文献[12-13]中实验及数值结果都能很好地吻合，证明了本文数值方法的准确性。

(a) 壁温分布

(b) 压降受Re的影响

图2 模型验证

2.2 结构对均温性的影响

微通道结构对均温性的影响见图3。图3a是入口流速为0.3 m/s时的壁温分布，各结构壁温都随通道长度的增加而增加，这是由于通道内流固耦合界面局部对流换热能力随通道长度增加而减弱，因此本文设计出口侧强换热能力的混合通道H-MCHS来提高其散热均匀性。R-MCHS壁面温升最大为348.47 K，壁面温差为28.27 K，其壁面温升和温差较大，均温性较差，因此后续主要对其他3种结构进行分析。H-MCHS同其他均匀结构相比具有均匀的壁温分布，壁面温差仅为5.9 K，相比于O-MCHS和OR-MCHS，壁面温差分别减小了49.10%和47.56%，显著提高了通道散热均匀性。同O-MCHS、OR-MCHS相比，H-MCHS均温性得到较大改善，其壁面局部热点由出口侧单一热点增加为出口侧、过渡区域前侧两处局部热点，过渡区域为H-MCHS斜截结构与含扰流肋的斜截结构过渡处。H-MCHS在过渡区域局部换热能力增强，使壁温下降，从而形成过渡区域前侧热点；而过渡区域后侧结构相同，通道散热能力随通道长度增加而减弱，从而使壁温上升形成出口侧局部热点。图3b清楚展示了不同流速下H-MCHS壁温分布及两局部热点受入口流速影响情况，当Vin<0.5 m/s时，过渡结构前侧热点温度小于出口侧热点温度，当Vin≥0.5 m/s时，过渡结构前侧局部热点温度大于出口侧热点温度。这是因为H-MCHS出口侧结构相比入口侧结构的换热能力受流速影响更大。

(a)Vin=0.3 m/s时不同结构的壁温分布

(b) H-MCHS不同流速的壁温分布

图3 微通道结构对均温性的影响

图4为不同结构温度云图和速度云图。从图4a可以看出：H-MCHS具有更均匀的温度分布，当通道长度为7～18 mm时，壁温保持在316～318 K，而O-MCHS与OR-MCHS壁面温度梯度较大。图4b取通道1/2高度处速度切面云图。O-MCHS主流道流体通过斜截通道流向相邻主流道，从而使主流道流动边界层不断发展，主流道与斜截通道流体相互混合进而强化通道壁面与流体间换热。OR-MCHS在斜截入口后方布置绕流肋，使流体更多地被分配到斜截通道内，增加斜截通道内流速，使斜截通道与主流道流体混合更加充分，同时增加换热面积，进一步强化通道换热。H-MCHS前半段采用斜截结构进行换热，后半段布置扰流肋斜截结构强化通道后方换热，从而有效减小因通道长度增加而导致壁温梯度过大的问题。

(a) 不同结构温度云图

(b) 不同结构速度云图

图4 不同结构温度云图和速度云图

2.3 入口流速对均温性的影响

图5为入口流速对壁面最大温升和压降的影响。如图5a所示，各结构壁面温升都随着入口流速增加而减小，增加入口流速可显著增加通道换热性能。OR-MCHS壁面温升最低，但其压降损失最大。如图5b所示，各通道压降损失都随着入口流速增加而增加。均温性最优的H-MCHS继承均匀通道结构O-MCHS、OR-MCHS结构特点，使其最大温升介于两均匀结构之间，其压降损失相比于O-MCHS增加了1.02倍，而比OR-MCHS减小了34.32%。这是由于含肋斜截结构虽然能提高换热能力，但压降损失较大。当入口流速从0.3 m/s增加到0.7 m/s时，3种结构的压降损失分别增加了2.19倍、2.25倍和2.09倍。

(a) 不同入口流速时壁面最大温升

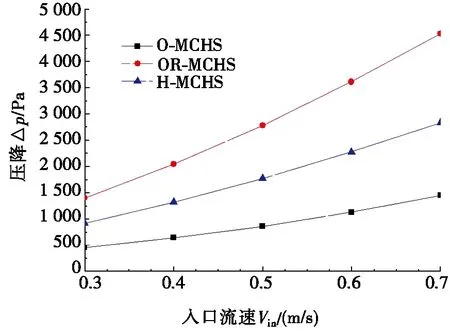
(b) 不同入口流速时压降

图5 入口流速对壁面最大温升和压降的影响

图6为入口流速对摩擦阻力因数和壁面温差的影响。如图6a所示，当入口流速为0.3 m/s时，OR-MCHS摩擦阻力因数f分别是O-MCHS和H-MCHS的3.03和1.53倍，随着入口流速增加，3种结构的摩擦阻力因数逐渐减小。图6b表明：增加入口流速可显著减小壁面温差。当入口流速增加到0.7 m/s时，3种结构壁面温差Td分别减小了78.76%、57.07%和50.33%，入口流速的增加极大地改善了壁面均温性。均匀通道O-MCHS、OR-MCHS壁面温差随入口流速增加而减小，且O-MCHS壁面温差减小幅度最大，H-MCHS壁面温差相对较低，且随入口流速的增加先减小再增加，当入口流速为0.5 m/s时达到最低值。虽然入口流速的增加提高了各结构换热能力，但各结构换热能力受入口流速影响程度不同。均匀结构通道壁面温差为进出口侧温度差，而H-MCHS因有2个局部热点，随着入口流速增加，过渡区域前侧热点温度大于出口侧热点温度，壁面温差由进出口间壁面温度差值变为进口侧与过渡区域前侧热点差值，而H-MCHS入口侧结构换热能力相对出口侧较弱，从而导致温差增加。

(a) 不同流速时摩擦阻力因数的变化

(b) 不同入口流速时壁面温差的变化

图6 入口流速对摩擦阻力因数和壁面温差的影响

图7为入口流速对Nuave和△Nuave/Nu0的影响。图7a对比了不同入口流速时各结构平均努塞尔数Nuave变化，3种结构Nuave都随入口流速增加而增加，OR-MCHS换热效果显著优于O-MCHS和H-MCHS。图7b为各通道结构在不同入口流速时△Nuave与入口流速为0.3 m/s时原结构努塞尔数Nu0的比值变化规律。随着入口流速增加，各结构散热能力都得到增强，尽管OR-MCHS散热效果最好，但O-MCHS的△Nuave/Nu0随着入口流速的增加而快速增大，表明O-MCHS换热能力受入口流速影响最大，对入口流速依赖性最高，但这也将导致过高的泵功损失和可靠性要求。

(a) 不同入口流速时Nuave的变化

(b) 不同入口流速时△Nuave/Nu0的变化

图7 入口流速对Nuave和△Nuave/Nu0的影响

2.4 综合特性分析

为了更加全面地分析O-MCHS、OR-MCHS和H-MCHS的综合特性，本文分析了相对于R-MCHS的强化传热因子η。η考虑通道流动阻力和换热的综合优化效果，由式(11)可知，η值越大，通道综合热性能越高。图8为综合特性分析。如图8a所示，η随入口流速先增加再减小。O-MCHS综合热性能显著优于其他结构。当入口流速为0.5 m/s时，O-MCHS综合热性能最佳；η=2.16时，H-MCHS综合热性能最低。这是由于H-MCHS前半段未布置扰流肋，相对削弱了通道换热，且后半段扰流肋的布置增加了流动阻力，导致整体综合热性能相对较低。将连续壁面离散成有限且足够多的点，则用壁温标准差刻画壁温的离散程度，壁温标准差由式(12)表示，壁温标准差越小，说明壁温偏离壁面平均温度的程度越小，壁面均温性越好。图8b展示了不同入口流速时壁温标准差σ，其中O-MCHS、OR-MCHS壁温标准差随着入口流速的增加而减小，增加入口流速可减小壁面温度梯度，当入口流速增加到0.7 m/s时，壁温标准差σ分别减小了79.57%和58.90%。H-MCHS壁温标准差σ相对较低，当入口流速为0.3 m/s时，壁温标准差σ仅为2.09 K，相比于O-MCHS、OR-MCHS，H-MCHS壁温标准差σ分别减小了53.76%和57.78%。入口流速从0.3 m/s增加到0.7 m/s时，H-MCHS壁温标准差σ减小了50.70%。当入口流速大于0.4 m/s时，H-MCHS壁温标准差σ趋于1 K。尽管H-MCHS的η值相对较低，但H-MCHS可在相对较低的入口流速下实现更均匀的壁温分布。

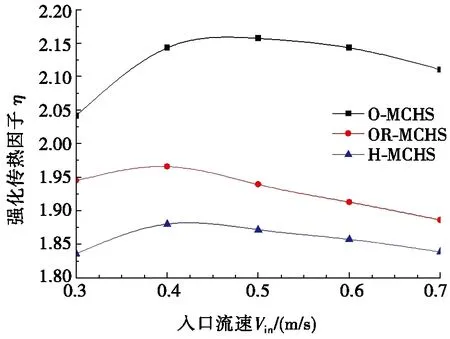
(a) 不同结构强化传热因子

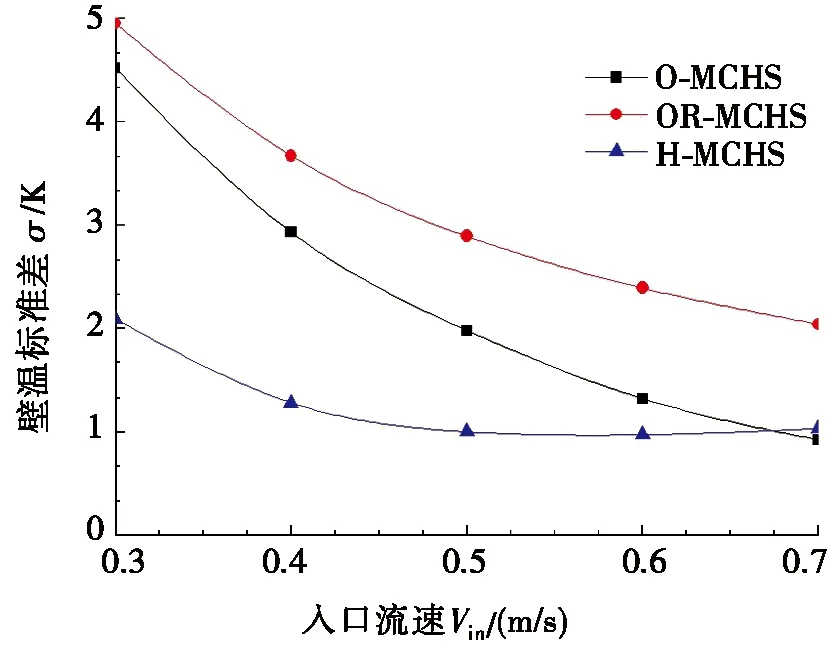
(b) 不同结构壁温标准差

图8 综合特性分析

3 结论

(1)当雷诺数Re较低(300～600)时，强化通道出口侧换热可显著改善通道壁温梯度过大的问题，使壁温分布更加均匀。当入口流速为0.3 m/s时，与O-MCHS、OR-MCHS壁面温差相比，H-MCHS分别减小了49.10%和47.56%，壁温标准差σ分别减小了53.76%和57.78%。H-MCHS的压降损失相比于O-MCHS增加了1.02倍，而比OR-MCHS减小了34.32%。

(2)在相同工况下，增加入口流速可以提高散热均匀性，但压降损失增加需要更大的泵功。当入口速度从0.3 m/s增加到0.7 m/s时，3种通道(O-MCHS、OR-MCHS、H-MCHS)壁面温差Td分别减小了78.76%、57.07%和50.33%，壁温标准差σ分别减小了79.57%、58.90%和50.70%，但压降损失分别增加了2.19倍、2.25倍和2.09倍。

(3)对于3种结构综合特性，O-MCHS综合热特性最好，其壁温标准差随着入口流速增加而减小。H-MCHS虽然综合热性能指标相对最低，但壁面温度梯度最小，壁温标准差σ最低且受流速影响较小。当流速大于0.4 m/s时，σ基本稳定在1 K。