WSN 节点定位技术的质心定位算法优化策略*
2020-12-23吴斌
吴 斌
(浙江邮电职业技术学院,浙江 绍兴 312366)
0 引言
新型无线传感器网络(Wireless Sensor Networks,WSN)影响了人们的生产、生活方式,被广泛应用于多个领域。在无线传感器网络应用中,要定位发生信息的位置,而没有信息位置检测的数据是没有意义的。只有提供可靠位置信息,才能够有效使用无线传感器网络收集的数据[1]。距离无关定位算法定位性能受到环境影响因素较小,能耗较低,且其定位精度能够满足大部分无线传感器网络的应用需求,为无线传感器网络定位技术学者研究的重点算法[2]。
1 质心定位算法的分析
1.1 RSSI 测距的原理
接收信号强度指示(Received Signal Strength Indication,RSSI)能够展现电磁波能量的大小数值。在距离不断增加的过程中,RSSI值不断减小,通过RSSI值计算锚节点的未知节点与距离。在发射端距离为d时,接收端通过测量表示RSSI存在随机误差,要求利用时间间隔抽样得出RSSI1(d),RSSI2(d),…,RSSI6(d)和算术平均值为:
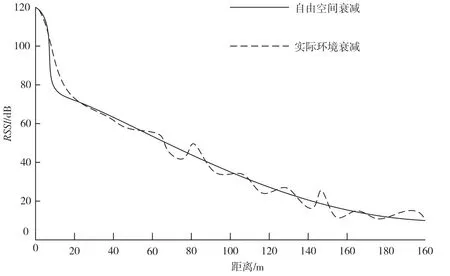
图1 接收信号强度衰减曲线
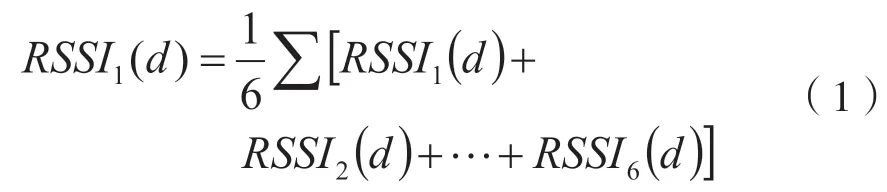
在实际使用过程中,电磁波传播路径损耗和理论值存在差别[3]。传播路径的损耗模型为:
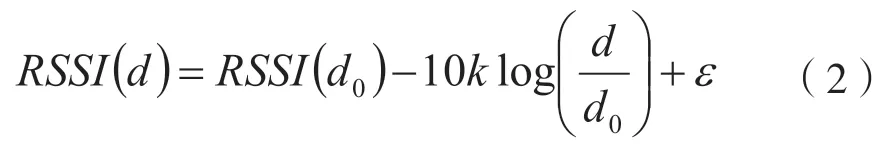
式中:d0为已知距离;d为接收端和发射源距离;RSSI(d)为距离发射源d所接收的RSSI值;RSSI(d0)为在发射端d0处所接收RSSI;ε为高斯分布随机变量,标准差为4~10;k 指的是衰减因子,范围为2~5。

接收信号强度衰减曲线详见图1。通过图1 可见,两者距离较远,通过RSSI距离误差得到扩大[4]。
1.2 三角形质心定位
理论上,WSN 各节点能够利用未知节点和3个锚节点距离,通过三边法计算其位置。但是,在实际使用过程中,要利用三角形质心法改善定位的精度。此方法的原理为:在未知节点H 接收锚节点发送信息时,将未知节点B 和锚节点的距离作为圆心计算,将d1、d2和d3作为半径画圆,D1、D2、E1、E2作为两两相交交点,计算ΔE1E2D1面积和ΔE1E2D2面积,将最小面积的ΔE1E2D2质心为未知节点H 估计坐标。通过节点H 接收n锚节点信号时,实现三角形的创建,从而得出未知节点坐标信息,利用质心算法得到坐标位置的最终位置[5]。
2 质心定位算法的改进
2.1 质心定位算法误差分析
质心精度和锚节点分布情况与密度相关。虽然使锚节点数增加能够改进定位精度,但是要使用多节点通信,增加节点能量消耗。另外,假如在未知节点周围使用定位锚节点,根据未知节点均匀分布,能够提高算法的定位精度,将会提高定位精度。相反,如果分布不均匀会降低定位精度[6]。图2 为未知节点周围分布参考锚节点情况对比。
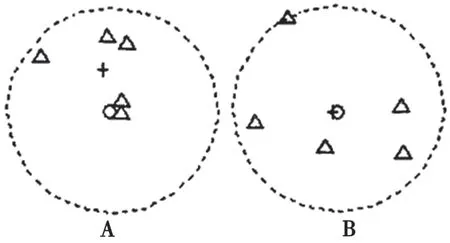
图2 未知节点周围分布参考锚节点对比
图1 中的小圆表示需要对未知节点进行定位,虚线圆为中心位置节点通信半径,三角形指的是定位计算锚节点。“+”指的是通过锚节点估计的坐标位置,B 中因为锚节点基于未知节点的中心分布均匀,定位比A 要精准。A 中的“+”指的是未知节点周围5 个锚节点求质心所得出的估计位置,通过图1 表示,距离未知节点最近的锚节点定位精度比较高。假如在B 中选择最近锚节点,那么精度较低。根据此情况,假如能够有效选择锚节点估计坐标,则能够提高定位精度。或者利用某方法降低因为分布不均导致的误差,从而改进定位精度[7]。
2.2 选择算法阈值
基于优化后的质心定位算法创建WSN 节点质心定位算法。此算法的特点是根据网络参数实际情况选择定位算法。假如N 值选择较大,那么未知节点临近区域中跳数比1 小的锚节点个数无法满足N值需求,算法会选择传统算法定位未知节点。这时会增加锚节点能量消耗,且加大计算开销和通信开销[8]。假如N 值选择较小,那么临近区域中未知节点跳数较小,锚节点数量会大于等于N 值,就会选择改进质心算法定位未知节点。在网络大部分未知节点同时利用改进质心算法定位的时候,虽然降低了锚节点能量、计算开销与通信开销,但是无法满足精准节点定位精度[9]。
2.3 创建测距模型
无线电传播过程中的环境、障碍物的影响,导致传播存在能量损耗,所以定位重点为对于多变环境选择合适能量损耗模型。能量损耗模型包括对数常态分布模型、对数据距离路径损耗模型和自由空间传播模型。根据实际使用经验,都是通过对数常态模型或者自由空间传播模型实现的,其中自由空间传播模型表示为:
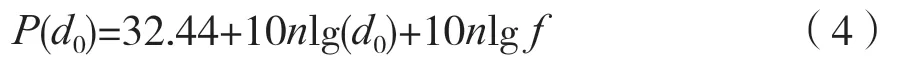
式中:P(d0)为路径损耗,接收端和发射端距离表示为d0;n指的是路径损耗系数2.5~4,表示无线电传播频率。
对数-常态分布模型为:
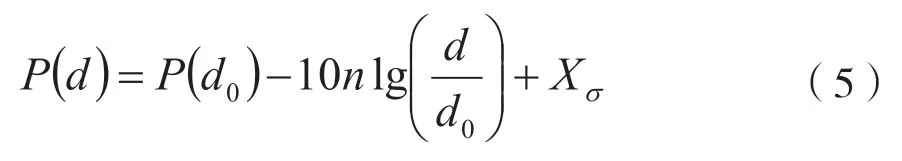
式中:P(d)指的是信号接收强度,P(d0)的d0为1;n指的是衰减因子;Xσ指的是高斯随机变量[10]。
在测距过程中,要创建RSSI与d相应的公式:

参数指的是环境参数,A和n都会对定位精度和测距造成影响。A与n的选值在环境等因素的不断变化过程中变化。在A为一定值时,同个位置能量值在n减少过程中增加。固定n不改变的时候,相同位置能量值在A减小过程中变大。所以,使定位精度和测距得到提高的主要方法是对不同环境使用不同A与n的值。A一般为-45 dBm,n的一般范围为2.5~4.0。
2.4 典型滤波方法和性能
2.4.1 均值滤波算法
均值滤波是指对周围周期性发送信息,并对数据进行接收。设置值为k,记录数据接收数量,对节点所发送数据时的个数进行记录,对已有数据个数是否大于等于k值进行判断。如果是,不接收,否则接收。最后,使收集的k个RSSI值实现求和运算,并且和k相除得到RSSI值,公式为:
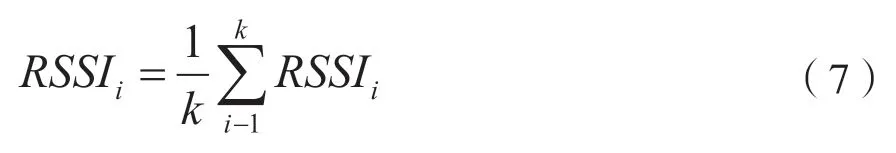
该方法简单方便,在收集数量较大时,信号处理能力较强。在数据波动较大时,RSSI值并不稳定,增加了误差,所以此方法一般应用到平均值附近的波动信号中。
2.4.2 中位值滤波算法
中位值滤波原理是指未知节点对周围周期性发送信息从而实现周围数据的接收。设置值为k,接收数据也就是RSSI值数量。接收到节点发送数据的时候,对数据数量是否大于等于k值进行判断,大于等于不接受,否则接收。最后,对收集的k个RSSI值进行排序,如果k为奇数,那么中间值就是最终值。如果k为偶数,那么中间值相加的一半是最终值,公式为:

此方法能够降低误差,在收集量低时具有理想的效果。采样较少的时候,它会增加误差。
2.5 改进算法实现
以上滤波原理和性能分析表示,两种算法的优劣势不同,所以本文使用其优点处理未知节点接收的采样值。此算法能够解决单个滤波算法缺点,提高测距准确度。和传统算法不同,此算法重点为解决传统测距阶段误差。首先,预处理未知节点的RSSI值后开展高斯滤波,加权修正RSSI值,提高测距精准度,在定位中使用,提高定位低精度。
未知节点规律性接收通信范围中锚节点位置信息,记录锚节点坐标信息与RSSI值。处理RSSI值的方法:首先,对RSSI值进行预处理,滤除波动比较大的数据;其次,利用预处理后RSSI值选择高概率区域,滤除突变因素导致高于真实值的数据;最后,加权修正高斯滤波后的RSSI值,最终得到RSSI值。
步骤1:RSSI值预处理。首先得出接收m个RSSI值平均,使m个RSSI值排序得到中位值。其次,实现平均值和中位值的平均值,即理想RSSI值。最后,使此组和理想RSSI值求差,和此理想值求比值,得出最大比值即RSSIrhread[11]:

式中,RSSIAVG为平均值,RSSIMID为中位值。
得出理想RSSI和阈值后,重新接收数据,通过式(10)和式(11)使接收的RSSI值和比值对应。如果一个RSSI值比RSSIrhread值要大,那么此数据无法满足真实值需求,缺乏参考性,需删除记录。
步骤2:对预处理后的RSSI值进行高斯滤波,使预处理后的k个RSSI值高斯滤波。
步骤3:高斯滤波后加权修正RSSI值,求筛选后n个RSSI值的平均值,根据式(11)求出RSSIAVG值后赋予n个RSSI值不同权值,将大权值赋予给和均值相差较大的值。最后,对权值进行归一化,以得到加权系数,从而得出修正后的RSSI:
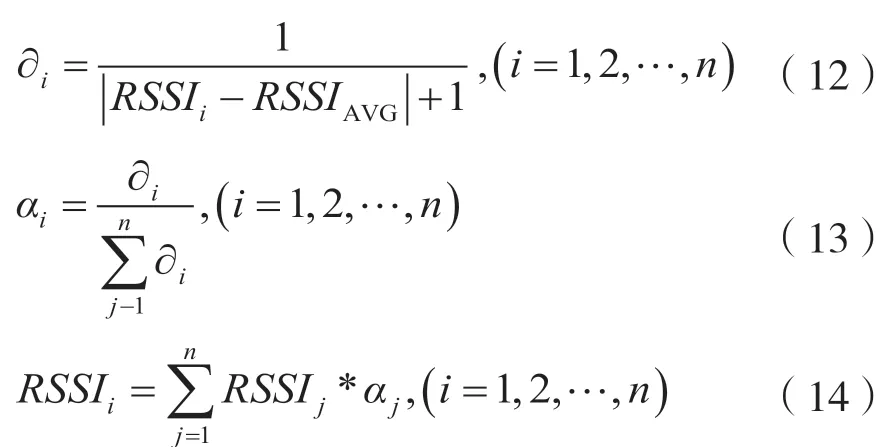
图3 为改进算法流程。
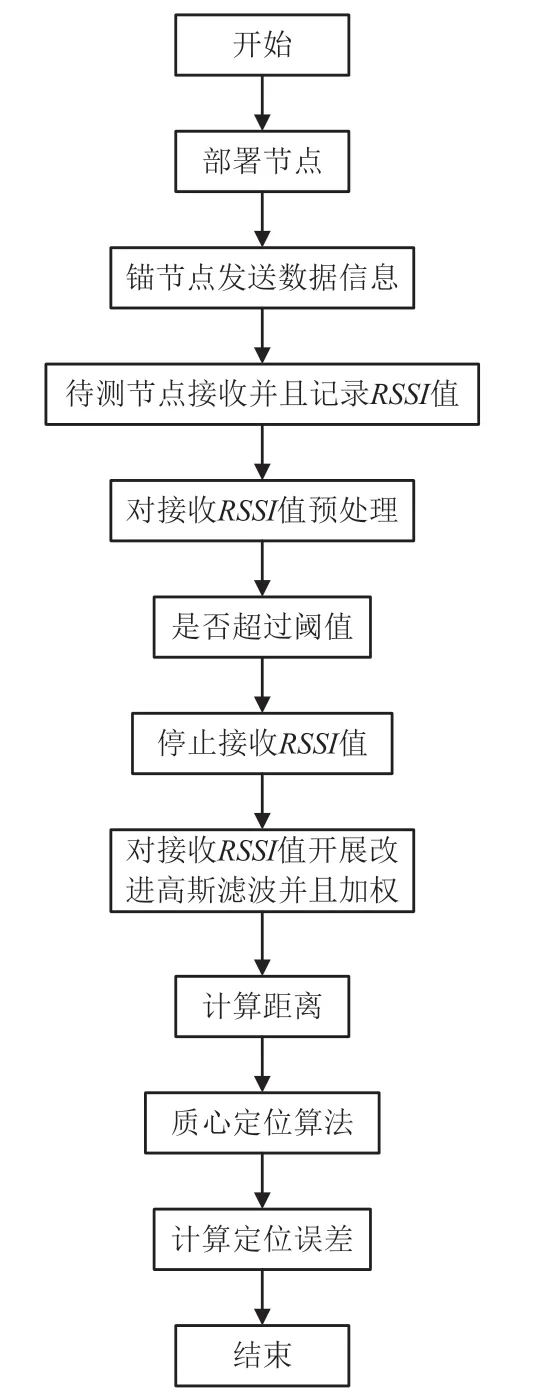
图3 改进算法流程
3 仿真结果分析
为了对本文所提出优化算法精准性和有效性进行分析,使用NS-2 仿真软件实现本文算法和传统算法的对比分析。假设仿真实验过程中的模拟区域为120 m×120 m 的区域范围,阈值N为4,节点总数为100 且均匀部署于正方形区域,节点通信半径为20 m。在锚节点数量不同的时候,图4 为不同算法定位误差曲线。分析仿真结果可知,在锚节点数量不断增加的时候,两种算法定位误差率都在改善。在锚节点个数比20 大的时候,本文定位算法误差率比传统算法要低,且锚节点数量越多定位越精准。表1 为锚节点改变时算法定位情况表。比如,在锚节点为20 的时候,优化定位算法有32 个,传统算法有48 个。锚节点只会对选择优化算法发送信息,所以降低了通信开销,还能够降低锚节点能量消耗。在120 m×120 m 区域中随机部署20 个锚节点,数量不改变且传感器节点总数量改变时,定位误差率在节点总数增加的过程中不断降低。在整个区域中,优化算法定位误差比传统算法要好[12]。
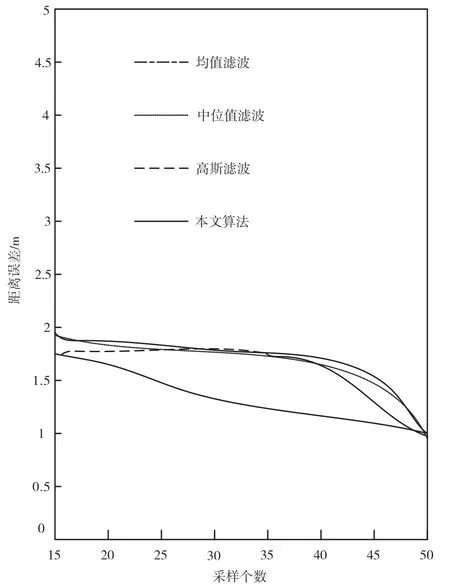
图4 不同算法定位误差曲线
4 结语
本文研究表明,优化算法能够改进传统质心算法的误差。在今后研究过程中,如何寻找处于未知节点周围均匀有效分布少数锚节点来开展质心算法尤为重要。使用质心定位算法比较简单,通信量较小,并且降低定位误差。
