基于混合图卷积网络模型的节点分类方法*

范 敏，范晓波，胥小波，康英来

（中国电子科技网络信息安全有限公司，四川 成都 610000）

0 引言

近年来，随着互联网和大数据的迅猛发展，图结构成为广泛应用的数据组织形式。例如，在社交和电商领域，大规模Web 系统产生的社交网络数据、黑产团伙数据等；在网络安全领域，各大安全产品可视化Web 界面中的资产关系图、攻击向量图等。在这些图数据中，节点表示单个用户或者资产IP 的行为特征，边表示用户或者资产IP 之间的互联关系。同时，虽然深度神经网络[1]（Deep Neural Networks，DNN）在语音识别、图像识别等机器学习问题中取得了很好的效果，但对于图结构这种非欧式数据仍处于早期研究阶段，其中语音和图像分别可以看成是一种具有固定序列（1 维序列）和网格结构（2 维网格）的图数据[2]。针对任意结构的图数据，以低维实空间中的向量数据形式表示节点属性和原始图结构的机器学习方法就是图表征学习[3]（Graph Representation Learning，GRL），常应用于节点分类、链路预测以及社群发现等任务。图表征学习可以分为节点嵌入（Node Embedding）和图神经网络（Graph Neural Network）两类方法。

第一类方法，节点嵌入。它以DeepWalk[4]、Node2Vec[5]、Struc2Vec[6]等模型为代表，仅考虑图的空间结构信息。例如，DeepWalk 通过随机深度游走的方式得到某个节点的邻居序列点，以此序列点作为该节点的上下文，然后利用Skip-gram 的思路训练得到该节点的特征向量。Node2Vec 是在DeepWalk 的随机深度游走基础上增加了随机广度游走信息序列。Struc2Vec 在保证原始图的结构信息前提下，通过将原始图映射为多层的图结构，然后再进行带偏置信息的随机游走得到上下文序列，最后利用Skip-gram方法训练得到节点的向量表征。此类方法仅仅使用了节点的标签特征，对节点具有高维附加属性的问题适用性较差。同时，由于没有参数共享机制，参数量复杂度为O(|V|)，其中|V|为图中节点的数量。随着图中节点数量的增加，参数量也会线性增加。

第二类方法，图神经网络。它以GCN[7]、GAT[8]、fastGCN[9]等模型为代表。它基于神经网络结构，能有效克服节点嵌入方法无法表达具有高维附加属性节点的问题，但是图神经网络的训练是一个难点。因为随着神经网络层数的增加，训练图神经网络不仅需要克服反向传播[10]中梯度消失、大量权重矩阵参数带来的过拟合等神经网络模型固有的问题，还需要克服图结构数据中存在的过渡平滑[11]（Over Smoothing）现象。过渡平滑是指应用多个图卷积层（大于2 层）后节点特征趋于同一向量，导致几乎无法区分的现象。这种现象最早在GCN 模型中被观察到[12]，作用类似于低通滤波器[13]。为了解决图神经网络中的过渡平滑问题，有两种典型方法。第一种，改变网络连接架构。例如：Xu K 等人[14]提出跳跃知识网络结构（Jump Knowledge Networks，JKN），利用跳跃连接为每个节点单独选择近邻范围，而不是固定数量的近邻聚合，从而实现了更好的局部结构注意力表征；Gong S 等人[15]提出几何原则连接结构（Geometrically Principled Connection，GPC），利用仿射残差连接改善了传统残差连接，进而更加高效地学习到了特定的映射转化矩阵。第二种，利用正则化技术。例如：Rong Y 等人[16]提出DropEdge 方法对图中的边进行随机Dropout，生成随机子图，类似于随机森林中的Bagging 思路，利用多样性实现正则化的目的；Zhao L 等人[17]提出PairNorm 方法，将节点特征之间的成对距离进行归一化；Zhou K 等人[18]提出NodeNorm 方法，将节点均值和方差归一化，而这些归一化技术通过阻止隐藏层节点之间或者节点特征之间的相关性学习降低了模型的平滑系数，防止了过度平滑。虽然上述的诸多方法通过各种方法和技巧使得训练深层的图神经网络得以实现，缓解了过度平滑问题，但是通常并不能带来性能的显著提升，反而会使模型复杂，降低实际的预测速度。表1 来源于参考文献[18]的表10～表12，每一类有15 个标签数据。可以看出，随着深度的增加，GCN-res（基线）的性能急剧下降，PairNorm和NodeNorm 表现一直良好。但是，深度的增加并没有带来模型性能的显著提升，甚至可能带来性能下降风险。例如：64 层NodeNorm 在CITESEER 测试数据集精度为67.49%，逊于2 层的GCN-res 的68.68%。

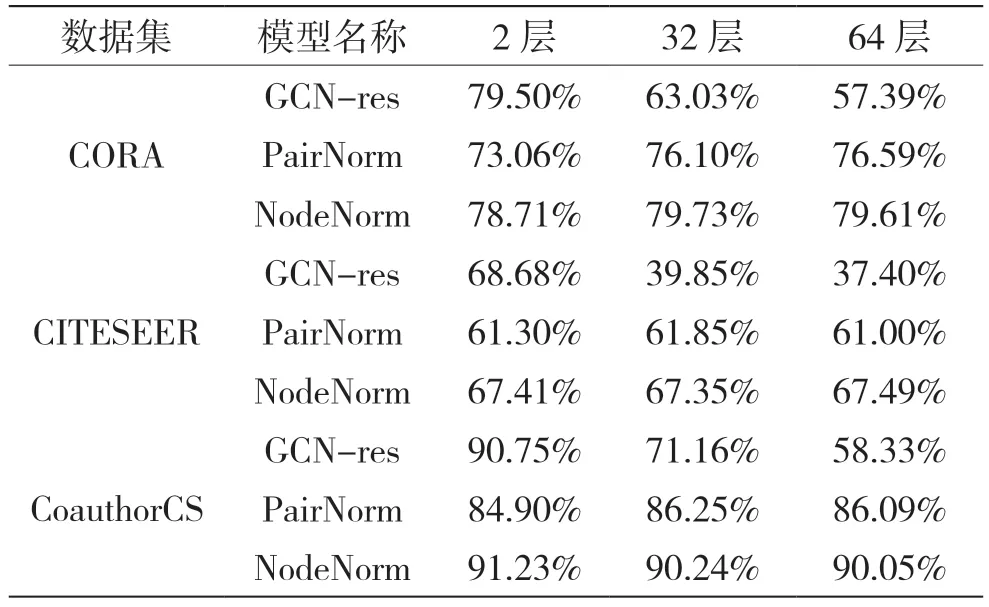
表1 CORA、CITESEER、CoauthorCS 测试数据集AUC

因此，本文从浅层网络和改变网络连接架构的角度出发，通过深入分析GCN 模型和GAT 模型的本质特征，结合图中节点的相邻相似性、结构相似性以及特征多样性，基于集成学习（Ensemble Learning）[19]的思路，利用组合式平滑操作增加原始特征的多样性，提出了混合图卷积网络模型（GCN Mixture Model，GCN-MM）。该模型一方面在GCN 模型中引入多个可学习的注意力矩阵，实现了对网络结构中边的重要性的刻画；另一方面，在GAT 模型中引入一阶切比雪夫多项式近似的谱图（Spectral Graph）[20]卷积，实现了对图网络结构中先验知识的保留，这样在GAT 模型中只需较少的注意力矩阵就能实现和原始GAT 模型相当的精度，同时改善了计算复杂度。

本文具体章节内容安排如下：第1 节深入分析GCN 模型和GAT 模型的本质特征；第2 节基于第1 节的分析，详细阐述提出的GCN-MM 的网络结构和数学表达；第3 节是在公共数据集CORA、CITESEER、PUBMED 上进行对比实验，并分析实验结果；第4 节总结全文。

1 相关工作分析

一张有n个节点、m条边的无向无环图由节点V={v1,v2,…,vn}和边E={e1,e2,…,em}的集合组成，其邻接矩阵、度矩阵和正则化的拉普拉斯矩阵分别为：

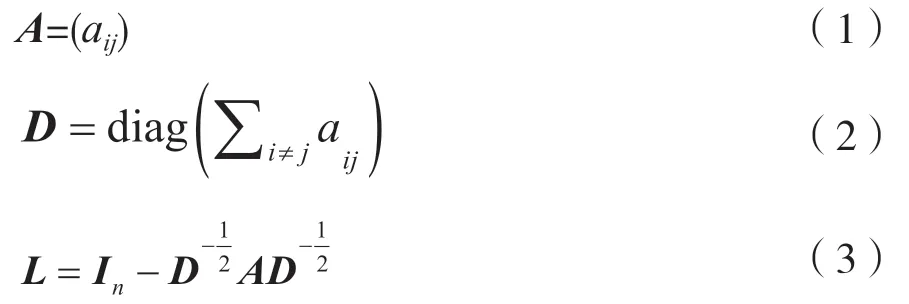
在谱图卷积中，图上的卷积操作需要将拉普拉斯矩阵进行特征分解得到特征值和特征向量，定义如下：

式中，x表示每个节点的标量，U表示拉普拉斯矩阵分解后的特征向量，ψ表示特征值。特征分解属于计算密集型，复杂度高，导致矩阵分解在实际应用中无法计算。此外，该卷积核是全局的卷积核，参数量随着图中节点数增加而增加，因此需要放松约束条件，利用空间采样或者谱采样方式近似拉普拉斯矩阵。例如，Donnat 等人[21]提出GraphWave 模型，利用Heat Kernel 来近似g(ψ)。

1.1 GCN 模型

GCN 模型通过引入切比雪夫多项式来近似g(ψ)，避免了矩阵分解，同时使用一阶近似也就是局部卷积核，避免了卷积核参数巨大的问题。

切比雪夫多项式定义为：

式中，T1(x)=x，T0(x)=1。

GCN 模型引入一阶切比雪夫多项式来近似g(ψ)，从文献[7]推导得出近似函数：

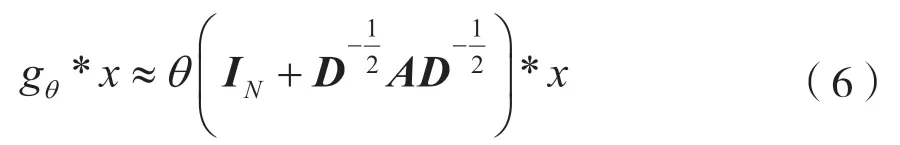
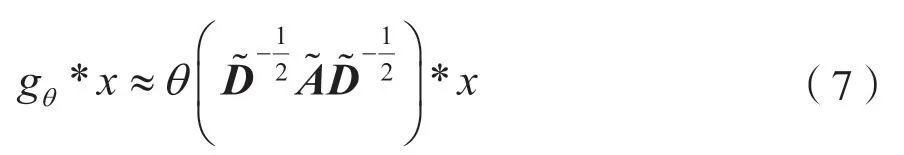
两层的图卷积网络为：

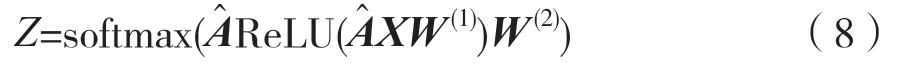
式中，W表示神经网络的连接权重，W(1)表示第一层神经网络的权重，W(2)表示第二层神经网络的权重，ReLU 和softmax 表示非线性激活函数，A^是单层卷积操作，即：

通过引入一阶切比雪夫多项式近似，使得从原先的全局卷积变为现在的局部卷积，即将距离中心节点1 跳的节点作为邻居节点，如图1 所示。每一次迭代，GCN 模型通过汇聚邻居节点1 跳的信息，避免了每次迭代都需要重新计算并更新整个图的卷积核参数，降低了计算复杂度。

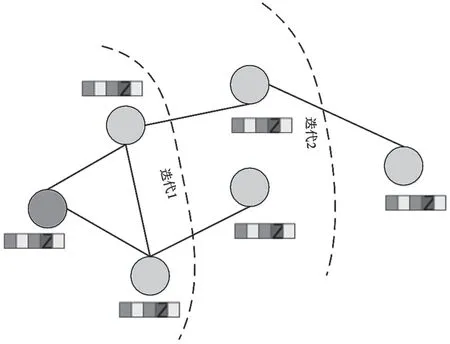
图1 GCN 模型

将式（8）进行可视化分解以便于理解，其模块示意图如图2 所示，其中H表示神经网络隐藏层向量。

1.2 GAT 模型

由于GCN模型假设图中所有的边重要性一样，也就是认为节点之间的连接关系重要度一样，因此在现实场景中是不合理的。文献[8]提出的GAT 模型通过引入多个注意力矩阵来学习图中相邻节点之间的重要性，即针对任意节点xi和节点xj，GAT 模型首先学习它们之间的注意力权重矩阵。注意力矩阵的数学表达为：

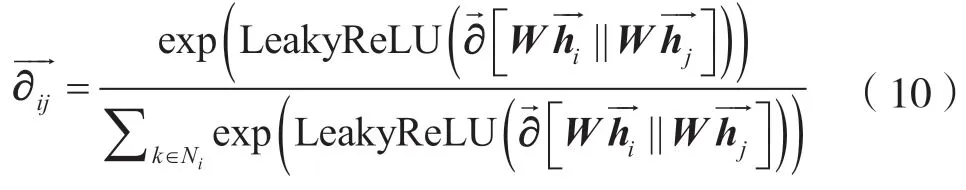
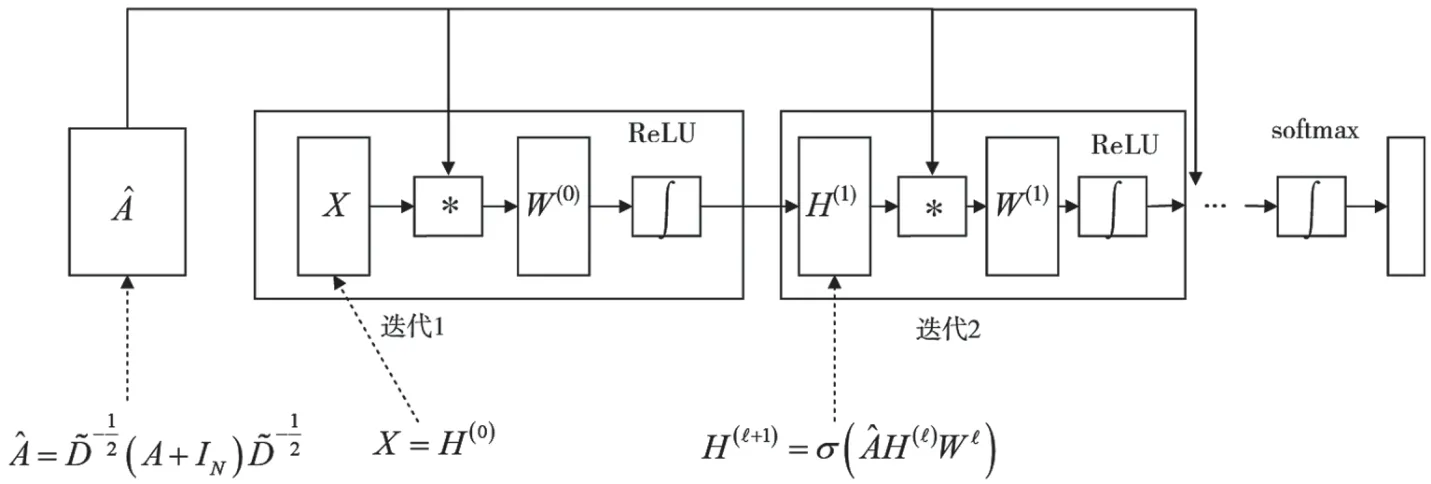
图2 GCN 模块

式中：LeakyRelu 是非线性激活函数；||代表将节点xi和xj的隐藏层表示进行拼接，然后进行归一化操作得到注意力权重矩阵，是非对称矩阵。这种非对称性对图中节点的重要性进行了区分。

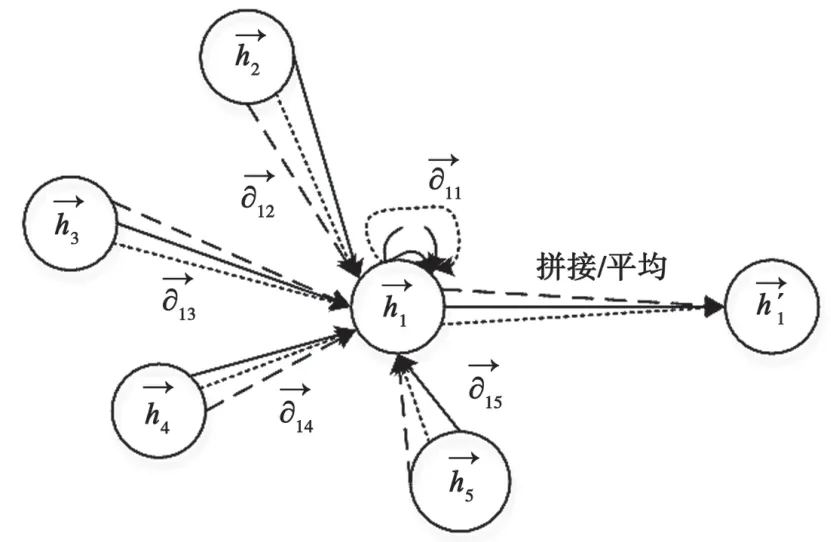
图3 GAT 模型

虽然GAT 模型通过学习近邻节点的权重实现了对近邻的加权聚合，使得对噪音近邻较为鲁棒，也赋予了注意力机制模型一定的可解释，但是因为引入了多个注意力权重矩阵也增加了模型的复杂度，导致计算比较耗时。

1.3 混合图卷积网络模型

本质上，GCN 模型是从谱域采样的角度，利用一阶切比雪夫多项式采样来近似图拉普拉斯矩阵，认为网络中所有的边的重要性是一致的，且每次只采样节点1 跳的近邻，是一种特殊形式的图拉普拉斯平滑操作。结合图2 和图4 的模块示意图对比，多个注意力矩阵通过引入对边的注意力矩阵来学习相邻相似性和结构相似性，本质上可以理解为是在近似的图拉普拉斯矩阵中进行局部重采样（reweighed）的过程。神经网络中卷积操作本质上是局部重采样，而多种不同尺度的卷积核是一种多样性特征抽取和表达。

2 提出GCN-MM 模型

2.1 GCN-MM 的网络结构

为了提升GCN 模型预测的准确性，同时提升GAT 模型的收敛速度，本文从浅层网络和改变网络连接架构的角度出发，提出了基于混合图卷积网络模型（GCN-MM）的节点分类方法，结构如图5 所示。

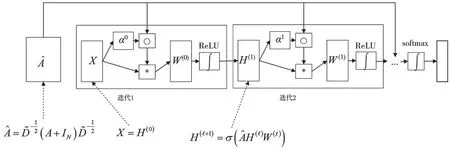
图4 GAT 模块

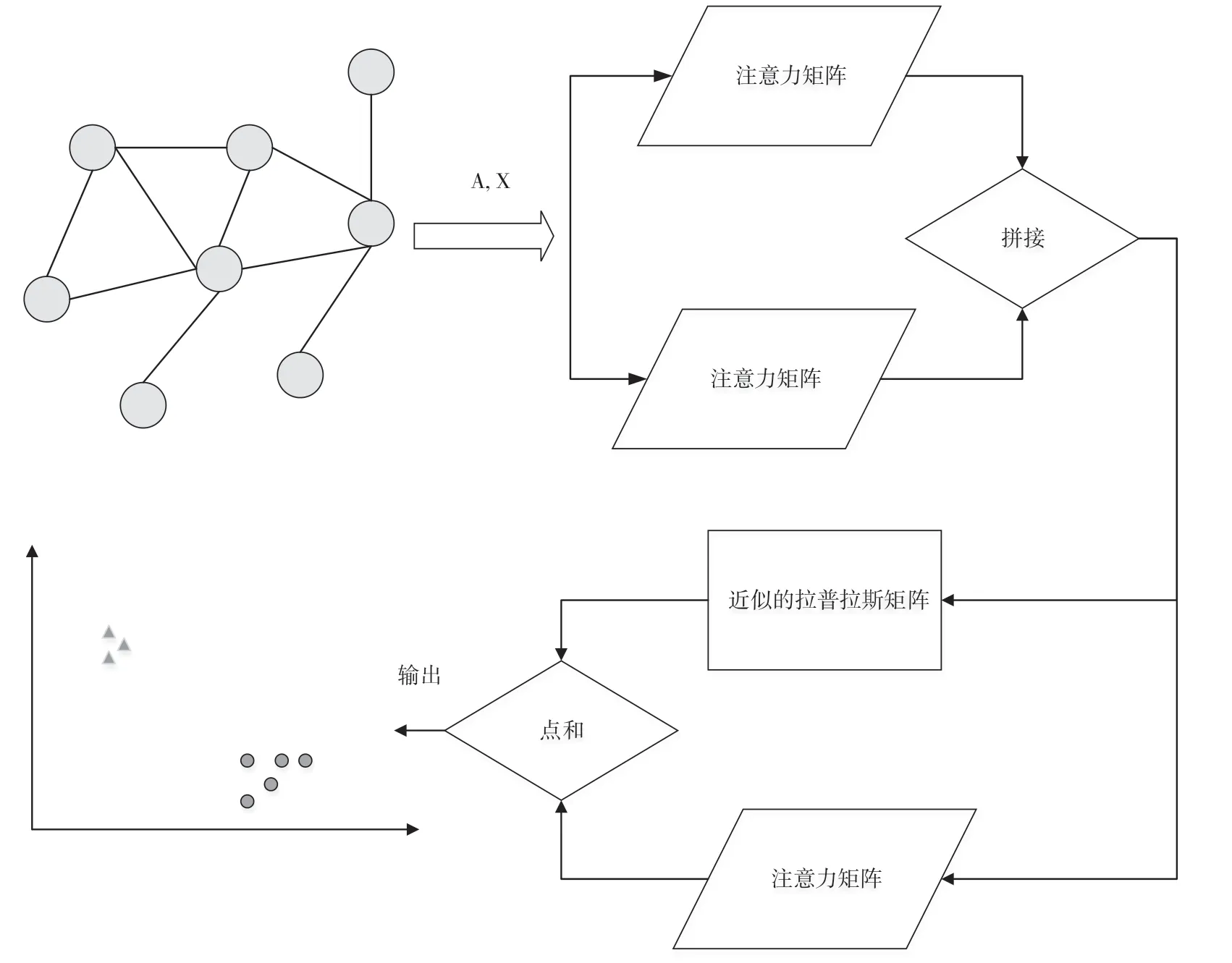
图5 GCN-MM 模型

首先，输入是一张无向连通图的一阶邻接矩阵和特征矩阵，输出是节点的分类标签结果。其次，混合结构的第一层仅使用2 个注意力矩阵（文献[8]的原GAT 模型使用了8 个注意力矩阵，2 层），第二层引入一阶切比雪夫多项式近似的图拉普拉斯矩阵和1 个注意力矩阵。最后，将第一层的输出进行拼接输入到第二层，而第二层的两个输出进行矩阵元素的点和操作作为最后的one-hot 分类结果。

在GCN 模型中，一张无向连通图被表示为半正定的图拉普拉斯矩阵，用于对图的空间结构信息进行数学描述。图卷积运算是对图拉普拉斯矩阵进行一阶近似。在GAT 模型中，图信息通过注意力矩阵传递给网络，而注意力矩阵刻画的是节点和其邻居节点的重要性关系，不是整张图。因此，本文提出的混合图卷积网络模型结构主要包含GCN 模型中的一阶切比雪夫多项式近似的图拉普拉斯矩阵和GAT 模型中的多个注意力矩阵两个部分。将以上两部分进行混合连接，不仅能够引入全局图的结构相似性，而且能够引入局部多样性表达特征，从而减少模型参数，大幅提升了训练速度，同时精度不受影响。

2.2 GCN-MM 的数学表达

从GCN-MM 混合模型结构中可以看出，该网络结构为浅层结构，共有两层。

第一层的数学表达式为：

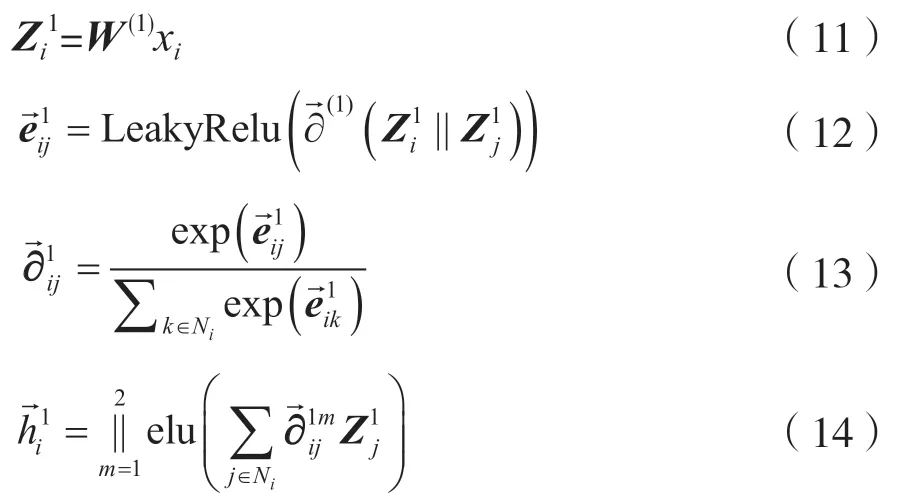
式中，LeakyRelu 和elu 表示非线性激活函数。式（11）中，xi表示第i个节点的特征，W(1)表示第一层网络的权重。式（12）中，表示第一层节点i和节点j之间的重要性系数。式（13）表示将重要性系数归一化到0～1，形成非对称注意力系数矩阵。式（14）表示利用两个注意力系数矩阵对节点i的周围邻居j进行拼接运算，得到节点i的第一层隐藏层输出。

第二层的数学表达式为：

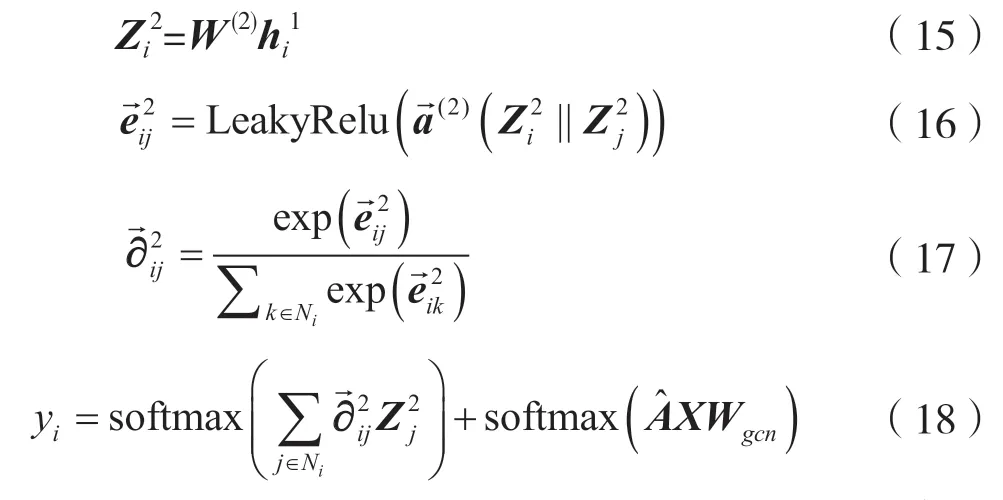
式（18）表示引入一阶切比雪夫多项式近似的谱图卷积，实现了对图网络结构中先验知识的保留。其中：A^ 是单层卷积操作，即式（9）；Wgcn表示GCN 模型学习的权重矩阵。

模型在训练时采用多分类交叉熵误差损失函数，公式为：

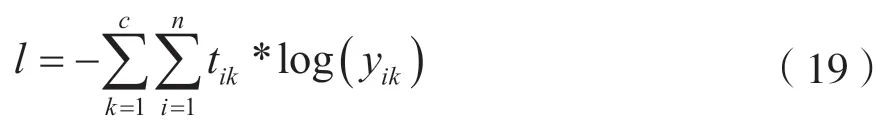
式中，tik表示样本i属于类别k的概率，yik表示模型对样本i预测为属于类别k的概率。整个神经网络使用经典的误差反向传播算法（Error Back Propagation）进行训练。

3 实验与分析

3.1 公共数据集

CORA、CITESEER 和PUBMED 是3 个文献引用网络公共数据集。这3 个数据集的图结构仅有一个连通分量，且都是直推学习（Transductive Learning）任务，详细信息如表2 所示。其中，节点数量表示文档数量，边数量表示文档之间的引用链接数量，特征数量表示文档的词汇特征，类别数量表示文档的类别，训练节点数量表示固定的训练集，验证节点数量表示固定的验证集，测试节点数量表示固定的测试集，标签率表示每个数据集中用于半监督任务训练的节点占比。另外，数据集中的节点全部都有标签，因此可以进行监督任务的学习。

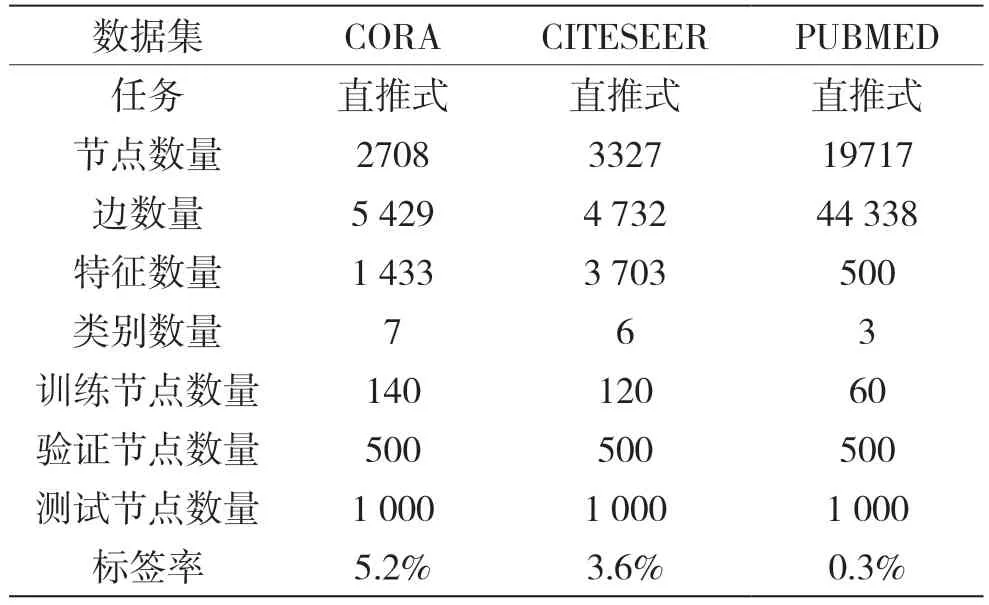
表2 数据集介绍

3.2 对比方法

本文将所提出的GCN-MM 混合结构模型在3个公共数据集CORA、CITESEER、PUBMED 上分别进行监督任务和半监督任务的比较实验。

文献[7-8]的半监督任务精度评价指标采用AUC（即ROC 曲线下的面积）。文献[9]提出的FASTGCN 模型通过将图卷积操作看作在概率度量下的积分变换，采用蒙特卡洛方法估计积分进行训练。它的监督任务评价指标采用Micro F1 Score（微观F1 分数）。为了公平比较，本文在对应任务中也采用同样的评价指标。速度评价指标采用训练耗时。训练耗时任务控制实验在同一台计算机设备（Intel（R） Xeon（R） CPU E5-2620 v3 @ 2.40GHz）中进行。

3.3 实验设置

本文提出的混合结构模型分为两层，输入是邻接矩阵A和特征矩阵X，输出是对节点所属类别概率的预测。第一层使用两个可学习的注意力矩阵模块，每一个矩阵模块的输出维度为8，因此进行Concatenate 后第一层的输出是16 维的特征，后使用指数线性单元[22]（Exponential Linear Unit，ELU）作为非线性激活函数。第二层包括一个一阶切比雪夫多项式近似的图拉普拉斯矩阵和一个可学习的注意力矩阵，输出的维度是类别个数，同时采用softmax 作为激活函数构建。为了防止过拟合，提高模型的泛化能力，在3 个数据集的实验中均进行了10-folds 交叉验证，同时依次采用了停止法（Early stopping）、L2 正则化以及Dropout[23]技术。

以CORA 数据集为例，本文提出GCN-MM 的具体网络结构如图6 所示。首先，将构建CORA 数据集的邻接矩阵和特征矩阵作为输入，邻接矩阵的维度是2708，特征矩阵的维度是1433。通过第一层的两个注意力系数矩阵后，输出维度为16。将这16 维的特征进行Dropout 层后，分别输入到第二层的一个注意力系数矩阵和近似的图拉普拉斯矩阵进行学习映射。最后，将两个映射输出的预测结果进行按矩阵元素Add 操作作为最终的预测结果。CORA 数据集共有7 类，因此输出的是7 维的one-hot 编码格式的向量。该向量是对目标变量的预测。

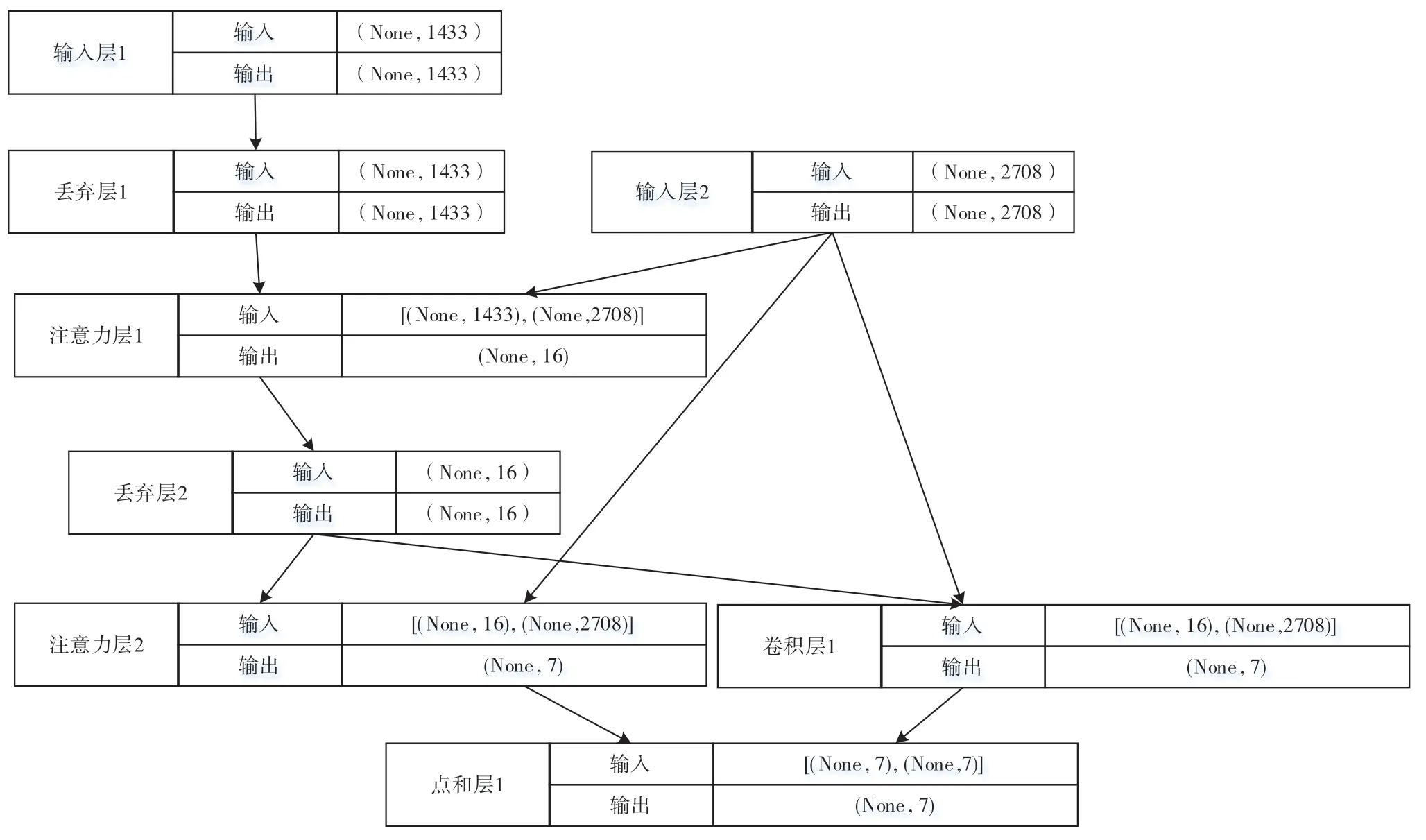
图6 Core 数据集的GCN-MM 结构

3.4 对比结果

对比结果主要分为两部分，包括CORA 和PUBMED 两个数据集的监督任务分类精度比较，以及CORA、CITESEER、PUBMED 这3 个数据集的半监督任务分类精度与训练速度比较。

3.4.1 监督任务

在监督任务上，因为FASTGCN[9]在CORA 和PUBMED 数据集上进行了监督任务实验，而论文GCN 模型和GAT 模型并没有进行监督任务的实验，所以在监督任务上与FASTGCN 中所给的数据进行比较。本文提出的模型监督任务的精度表现如表3所示。从表3 可以看出：在CORA 数据集的监督任务中，提出的模型Micro F1 Score 比原始的GCN 模型增加约1%，比GCN 模型的加速版FASTGCN 模型增加约3%；在PUBMED 数据集的监督任务中，提出的模型Micro F1 Score 比原始的GCN 模型增加约2%，比GCN模型的加速版FASTGCN模型增加约1%。

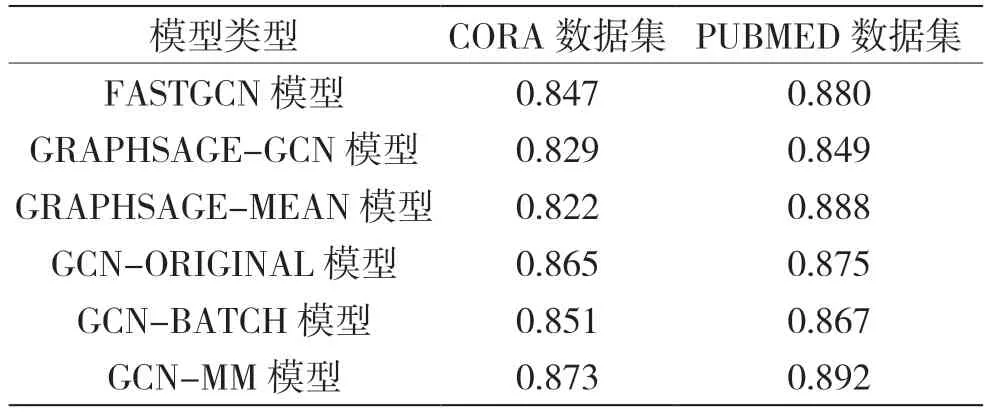
表3 监督任务微观F1 分数比较

监督任务整体柱状图如图7 所示。

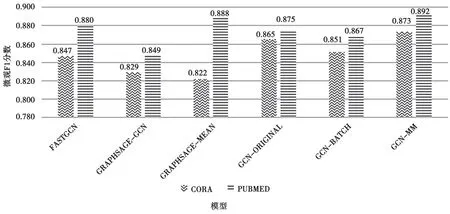
图7 监督任务直方图比较

3.4.2 半监督任务

在半监督任务中，由于文献[8]给出了GAT 模型在CORA、CITESEER 和PUBMED 这3 个公共数据集中和GCN 模型的对比，因此本文的半监督任务也在3 个数据集中进行对比。各个数据集的半监督任务标签率如表2 所示，CORA 数据集标签率是5.2%，CITESEER 数据集标签率是3.6%，PUBMED数据集标签率是0.3%。

为了保证实验公平性，在比较训练耗时的任务中，迭代次数（Epoch=2000）和停止法（Early stopping=100）两个参数保持一致，则提出的模型半监督任务的训练耗时表现如表4 所示，单位是秒，精度AUC 如表5 和图8 所示。从表4 可以看出，在CORA、CITESEER 和PUBMED 这3 个公共数据集中，提出的模型在模型参数和训练速度上介于GCN 和GAT 之间。因为GAT 在GCN 基础上进行了边的重新采样，且原始论文中第一层GAT 利用8 个Head，因此模型参数量大、较耗时，而提出的模型只用了2 个Head。

表5 是半监督任务的精度AUC 分数表现对比情况。

表4 半监督任务训练时间比较/s

表5 半监督任务AUC 比较

为了更清晰地进行对比，可以将表5 形成柱状图，如图8 所示。

结合表4 和图8 可以看出，GAT 模型训练耗时大于3 天（259200 s），而提出的模型相比GAT 模型在减少模型参数和训练耗时的前提下并没有影响模型的精度。

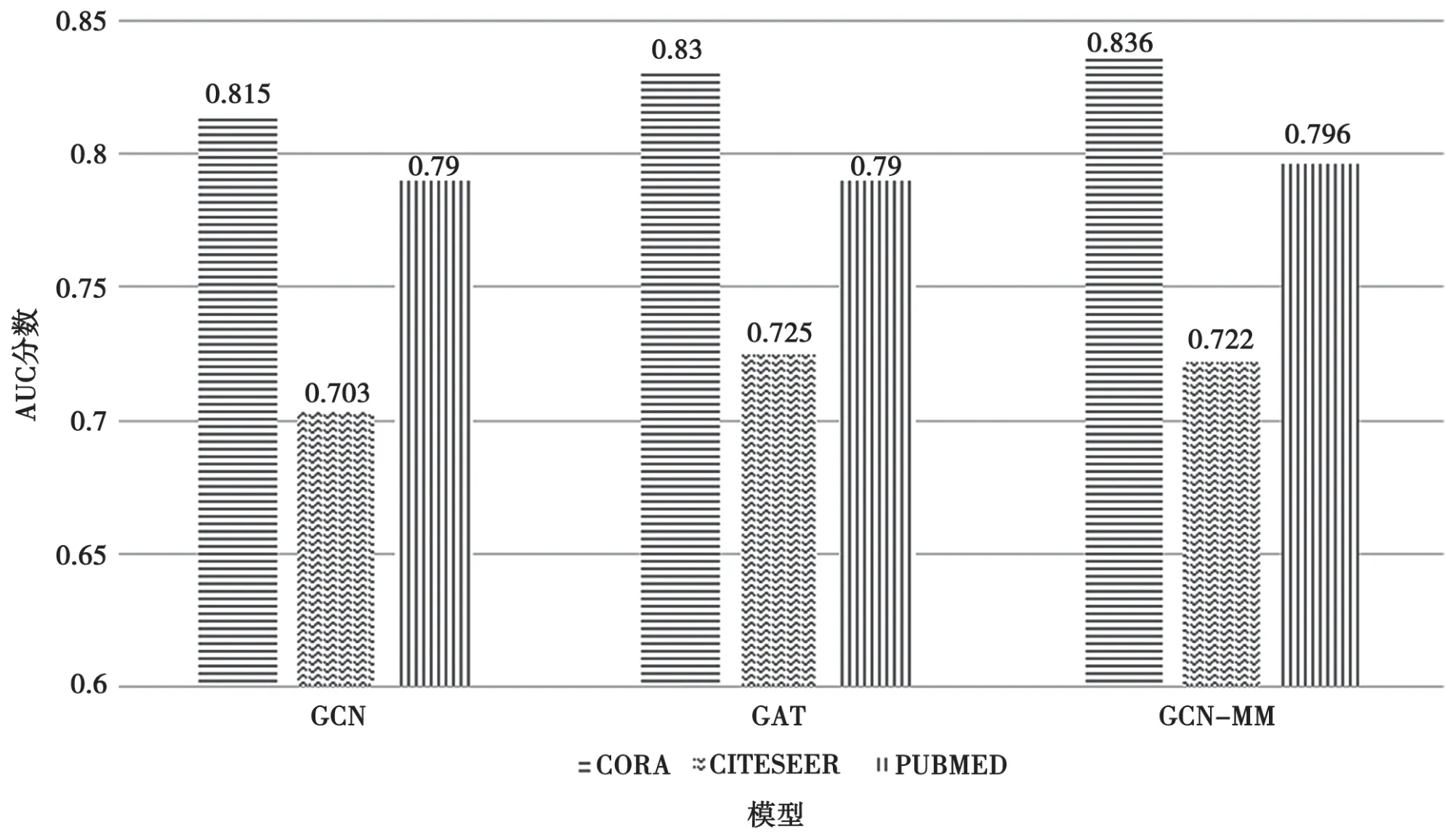
图8 半监督任务直方图比较

4 结语

本文利用GCN 模型的全局特性和GAT 模型的局部特性，结合网络节点的相邻相似性、结构相似性以及特征多样性表达3 个方面，提出了一种混合图卷积网络模型。该结构一方面引入GCN 模型中的一阶切比雪夫多项式近似的图拉普拉斯矩阵提高了运算速度，另一方面引入GAT 模型中的多注意力矩阵提高了分类精度，能有效克服纯GCN 带来的精度缺陷和纯GAT 模型带来的速度缺陷，减少可调整参数数量和训练耗时，同时不影响模型精度。未来，在该框架下，网络结构的设计还可融合更多的模型，如Graph-SAGE 模型，以提供新的多样性表达而不必局限于本文所使用的两种网络结构，使模型具有更强的扩展性。