基于改进生物地理学优化算法的分布式装配置换流水车间调度问题

2020-12-23黄佳琳张丫丫顾幸生

华东理工大学学报(自然科学版) 2020年6期

黄佳琳，张丫丫，顾幸生

（华东理工大学化工过程先进控制和优化技术教育部重点实验室，上海 200237）

置换流水车间调度问题(Permutation Flowshop Scheduling Problem, PFSP)是制造系统和工业过程中广泛研究的组合优化问题[1]，通常假设所有的工件都在一个工厂中进行加工，即单一工厂生产模式。现如今，在全球化的背景下，分布式制造以低成本、低风险、高质量的优势取代了单一工厂生产模式，成为工业生产过程中的主流形式。比起单一工厂调度问题，分布式制造的调度问题更为复杂。它不仅需要考虑工件在机器上的加工顺序，还必须考虑如何将工件合理地分配到相应的工厂进行加工。不同工厂的不同工件分配会形成不同的调度方案，从而影响供应链的绩效[2]。

装配流水车间调度问题(Assembly Flowshop Scheduling Problem, AFSP)广泛存在于生产制造系统中，用于生产由不同工件装配而成的多种产品[3]。考虑到装配系统在工业过程中的实际应用，装配流水车间调度问题也是生产调度领域的重点问题。装配流水车间是一个混合生产系统，其中各个生产操作都是独立并且同时执行的，以便将工件运输到装配线，及时进行产品的组装。在组装过程中，可以由给定数量的不同工件根据装配程序制造各种各样的最终产品，装配程序代表了由不同供应商提供的不同工件之间的组装关系[4]。

分布式装配置换流水车间调度问题(Distributed Assembly Permutation Flowshop Scheduling Problem,DAPFSP)是分布式置换流水车间调度问题和装配流水车间调度问题的结合，最早由Hatami 等[5]提出。Hatami 等针对DAPFSP 问题，以最小化装配工厂完工时间为目标，提出了基于不同结构的启发式算法和可变邻域下降(VND)算法等12 种方法。在此基础上，越来越多的优化算法被应用于求解DAPFSP问题。2016 年，Wang 等[6]提出了基于分布估计算法的模因算法(EDAMA)来求解DAPFSP 问题，通过与文献[5]的12 种启发式与元启发式算法比较，验证了 EDAMA 算法的优越性。2017 年，Lin 等[7]采用回溯搜索超启发式(BS-HH)算法，同样与12 种方法以及EDAMA 等智能优化算法进行比较，突出了BSHH 算法的有效性。2019 年，Pan 等[8]针对新型 DAPFSP问题的不同的CPU 时间和解决方案质量的需求，提出了一个混合整数线性模型，还列出了3 种不同结构的启发式算法、两种可变邻域搜索方法以及迭代贪婪算法，最后在算法性能和运算时间两方面与其他16 个已有算法进行对比，结果表明所提算法能够高效地解决新型DAPFSP 问题。

生物地理学优化(Biogeography-Based Optimization, BBO)[9]算法自提出以来，因对问题依赖度小、算法参数少、易于实现等优点备受青睐。Rahmati 等[10]采用BBO 算法求解包含3 个目标函数的柔性作业车间调度问题，并且对遗传算法和BBO 算法进行比较，利用基准测试数据（Brandimart 数据）以及Barnes和Chamber 数据的运算，凸显了BBO 算法的优势。Lin 等[11]采用和声搜索算法和基于对立的学习方法改进BBO 算法来求解专色印刷的专色匹配问题，通过与粒子群算法的比较，验证了BBO 算法的有效性。然而，BBO 算法存在收敛速度缓慢、易陷入局部最优解以及在规定迭代次数中难以获得最优解等缺点[12]。考虑到分布式装配置换流水车间的加工特点，本文设计了3 种改进策略：首先，使用加工时间最短优先（Shortest Processing Time，SPT）规则和 NR2规则改善初始可行解的结构；其次，在变异过程中加入基于工厂完工时间的工件插入启发式方法，优化工件的工厂分配策略及其在各工厂内的加工顺序；最后结合模拟退火算法，跳出局部最优，提高算法寻优的质量。仿真结果证明了改进的BBO 算法求解分布式装配置换流水车间调度问题的有效性。

1 分布式装配置换流水车间调度问题

1.1 问题的描述

分布式装配置换流水车间调度问题包括两个阶段：生产阶段和装配阶段，并且可以概括为3 个子问题：工件调度、产品调度和工厂分配，如图1 所示。

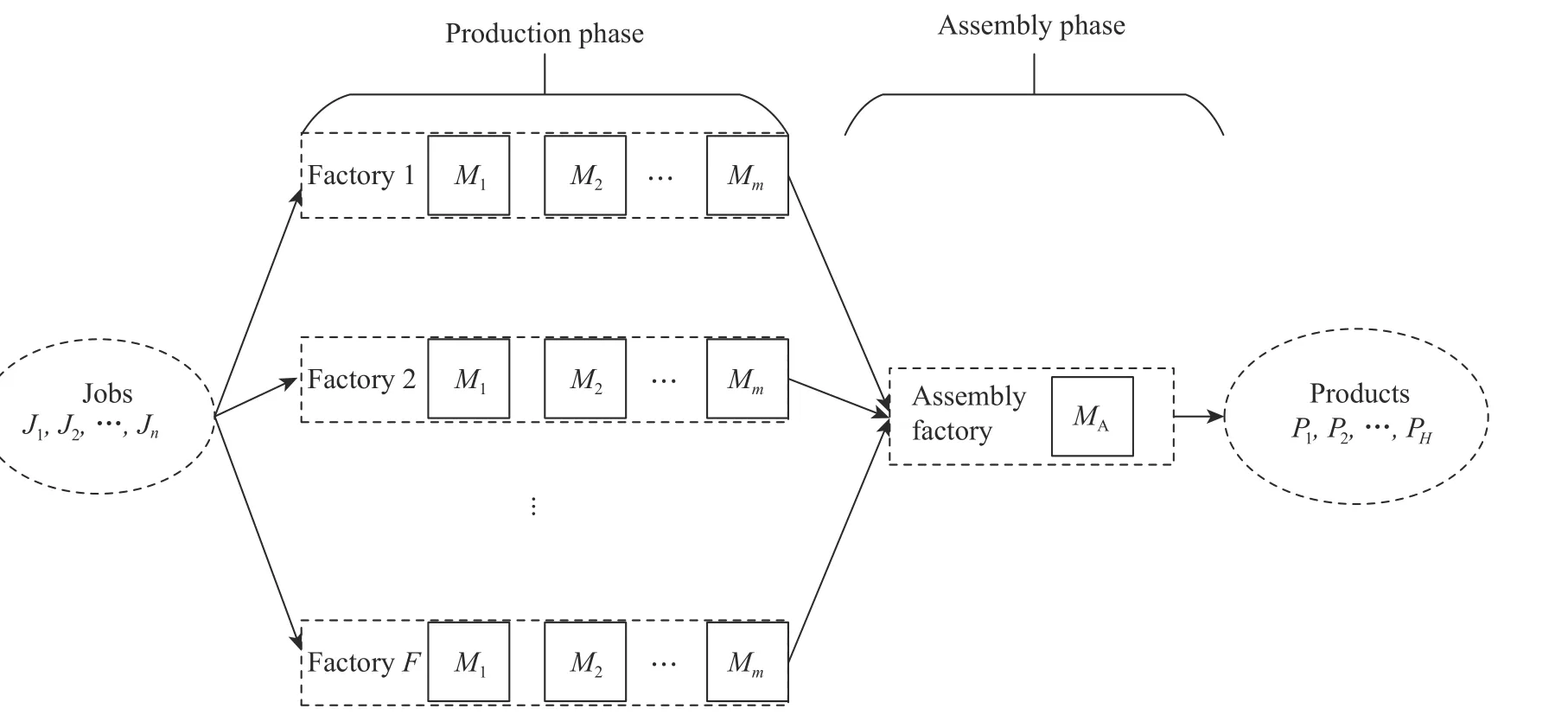
图 1 分布式装配置换流水车间调度问题Fig. 1 Distributed assembly permutation flowshop scheduling problem

1.2 模型的目标函数

2 生物地理学优化算法

BBO 算法是一类基于种群和生物启发的群智能优化算法，其核心是栖息地间种群的迁移和变异过程，同时这两个过程也是算法实现优化操作的主要步骤。

2.1 生物地理学优化算法的设计原理

生物种群分布于不同的栖息地，各栖息地都可用对应的适宜度指数(Habitat Suitability Index,HSI)来表示。与HSI 相关的特征包括栖息地的降雨量、植被的多样性和气候等因素，构成了一个描述栖息地适宜度的向量SIV(Suitable Index Vector)[15]。应用BBO 算法求解优化问题时，一个栖息地对应优化问题的一个可行解，通过计算各栖息地的适宜度值来评价这些解的优劣程度。根据不同栖息地之间物种的迁移操作和栖息地内物种的变异操作，使适应度值较差的栖息地获得更多适应度值较好的栖息地的信息，实现栖息地的不断进化[16]。

2.2 生物地理学优化算法的迁移操作

BBO 算法通过迁移算子实现栖息地之间的信息交互，从而达到进化的目的。栖息地的适宜度值越高，其所能容纳的物种数量越多，反之则越少，这就需要建立一个表征物种数量与栖息地适宜度关系的映射函数[17]。BBO 算法根据各个栖息地的适宜度值，从大到小进行排序，设栖息地数量为P，最大物种数为 Nmax，则栖息地 n 的物种数量 N(n)=Nmax-n，n=1, 2, …, P（n 是各栖息地经过排序后的序号）。物种在栖息地之间的迁移操作根据迁出率μ(n)和迁入率λ(n)进行，各栖息地的μ(n)和λ(n)的计算公式如式(8)、式 (9)所示：

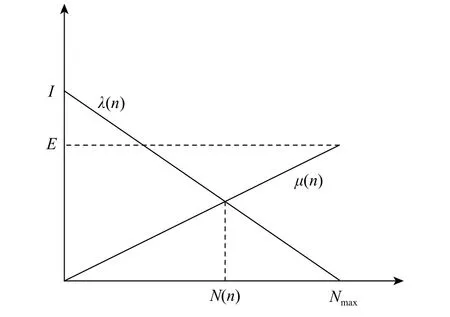
图 2 迁入率、迁出率与物种数量的关系Fig. 2 Relationship between immigration rate, emigration rate and species quantity

2.3 生物地理学优化算法的变异操作

突发的灾难性事件能够完全改变一个栖息地的生态环境，导致栖息地的适宜度值产生巨变，生物地理学中通过变异来模拟这一情况[19]。BBO 算法根据变异概率随机地修改栖息地的特征向量，变异概率主要取决于栖息地的物种数量概率，也可以说和栖息地的物种数量息息相关。物种数量为N(n)的栖息地发生变异的概率 mn如式(10)所示：

3 MBBO 算法求解 DAPFSP 问题

3.1 编码与解码

应用改进的生物地理学优化(MBBO)算法求解分布式装配置换流水车间调度问题时，在初始化阶段将采用两种不同的编码方式生成初始可行解，分别称为规则解和随机解。

规则解主要是根据SPT 规则生成。将每个产品中的工件按SPT 规则进行排列，确定每个产品的工件加工顺序。在此基础上，计算每个产品的装配开始时间，并规定最早开始装配的产品排在前面，由此产生产品序列。两者结合即为一个完整的工件加工序列，这样产生的规则解是唯一的。最后采用NR2规则进行解码。NR2规则定义为[13]：将工件 j 分配给包含工件j 之后最大完工时间最小的工厂，由此生成新的调度方案。

随机解引入了“虚拟工件”的概念，其包含了工件和工厂两种因素。首先，将所有工件进行随机排列，生成一个工件加工序列；然后，将工厂作为“虚拟工件”，插入到已有的工件加工序列中，“虚拟工件”的个数同工厂的数量一致，并且“虚拟工件”用数字“0”表示。需要注意的是，每个随机解的第1 列必须是“虚拟工件”，即必须为“0”，否则将存在不能在任何工厂加工的工件，这样的随机解就变成了不可行解。除此之外，若随机解存在两个“虚拟工件”相邻的情况，就表示存在某个工厂处于闲置状态，不加工任何工件。这样的解虽然属于可行解，但根据实际生产过程可以判断，此类解的适应度值一般比较低。为了提高初始可行解的质量，MBBO 算法以将工件均匀分配给各个工厂的方式生成新的初始解，取代存在工厂闲置情况的初始解。随机解的解码根据最大完工时间的计算公式进行计算。

以 8 个工件、2 台机器、2 个工厂、2 个产品的分布式装配置换流水车间调度问题为例，隶属于2 个产品的工件分别为：产品1={1,2,4,8}，产品2={3,5,6,7}。对于规则解，所有工件按SPT 规则排列后，每个产品的工件加工顺序如下：产品1={8,1,2,4}，产品2={7,5,3,6}，此时，两个产品的开始装配时间分别为：产品1=127，产品2=133，则规则解的工件排序如图3 所示。最后根据NR2规则解码，得出规则解的具体形式及最大完工时间 Cmax(Λrule)=501 ，规则解的具体形式如图4所示。

图 4 规则解的具体形式Fig. 4 Specific form of rule solution

针对这个例子，随机解就是利用randperm 函数对1～9 进行随机排序，并把大于8 的数置零，最后在首位插入一个“0”。随机解的数量很多，从中挑出一个，其具体形式如图5 所示。

图 5 随机解的具体形式Fig. 5 Specific form of random solution

3.2 按照适应度值排序

在执行精英保留策略、迁移操作和变异操作之前，需要计算各个栖息地即各个初始可行解的适应度值，并按照从大到小的顺序进行降序排序，最优解排在第一位。

3.3 精英保留策略

BBO 算法在迭代过程中有可能生成适应度值更高的解，若不对这些优良解采取保护措施[17]，放任它们参与迁移操作和变异操作，很容易破坏优良解的结构，丧失获取更优可行解的机会，导致算法的搜索能力下降。MBBO 算法加入了精英保留策略，即在每次执行迁移和变异操作之前，取初始可行解数量的10%作为精英解，不作任何改变，而是保留到下一步迭代过程再进行相应操作。

3.4 迁移操作

BBO 算法通过迁移操作，用较优解中的元素来取代较差解中的元素，以此实现栖息地之间的信息交互。MBBO 算法的迁移操作和BBO 算法的迁移操作大同小异。对每个解，在执行迁移操作时，改进前后的算法同样都是按位进行循环，根据迁入率判断该位是否发生迁入，若发生迁入，再根据轮盘赌法选择迁出的位，进行相应位的交换操作。MBBO 算法有两个特别之处：第一，对于规则解，规定其不参与迁移操作。因为规则解的特色就在于它是产品序列和各产品工件序列的结合，每个产品的工件不能分开，否则将会影响产品的装配开始时间，进而影响解的结构，致使该解失去作为规则解的优势。第二，对于随机解，在按位循环判断是否发生迁入或是根据轮盘赌选择迁出位的时候，都必须跳过每个解的第一位（第一位都是“0”，即“虚拟工件”），否则将会生成不可行解。

3.5 改进的变异操作

BBO 算法利用变异操作来保证解的多样性，抑制算法的早熟现象。BBO 算法的变异过程是根据变异概率判断解（栖息地）的某个特征分量是否发生突变，具体操作与迁移过程相似。首先按位进行循环，根据变异概率判断该位置元素是否发生变异，若发生变异，则随机选择变异的位，进行合法交换即可。然而，BBO 算法的变异过程随机性较大，很有可能破坏之前的优势解，因此MBBO 算法对此进行了改进，加入了基于工厂完工时间的工件插入启发式方法。在MBBO 算法的变异过程中，利用变异概率判断某个解而不是解的某个特征分量是否进行突变，若确定该解发生突变，则依次将该解中完工时间最大的工厂的每个工件插入到该解中完工时间最小的工厂的工件序列中，并找到最佳的插入位置。插入最佳位置后，比较新解和旧解的工厂最大完工时间，若新解的工厂最大完工时间小于旧解的最大完工时间，则接受新解，反之，则返回旧解。基于工厂完工时间的工件插入启发式方法的伪代码如下：

3.6 模拟退火算法

为了提高解的质量，MBBO 算法还结合了模拟退火算法，有助于跳出局部最优解，增强算法的搜索能力。

考虑到MBBO 算法的效率问题，在算法迭代过程中，记录每次的最优值，若在最后20 次的迭代过程中，最优值都保持不变，则对得到的最优解采用模拟退火算法进行进一步寻优。模拟退火算法的伪代码如下：

3.7 MBBO 算法求解 DAPFSP 问题

MBBO 算法求解DAPFSP 问题的过程中，可行解表示栖息地，每个可行解都由一个行矩阵表示，而栖息地中的物种由矩阵中的元素及它的位置信息共同表示。适应度值对应着于目标函数值的倒数，目标函数值即式(7)计算出的值。MBBO 算法求解DAPFSP 问题的具体流程如图6 所示。

4 仿真实验

为了验证改进的生物地理学优化算法求解分布式装配置换流水车间调度问题的有效性，对两组基准数据（http://soa.iti.es）进行仿真计算。每组数据由4 个变量组成：n（工件数）、m（机器数）、F（工厂数）、H（产品数）。第1 组由900 个小型实例组成，其中，n={8,12,16,20,24}，m={2,3,4,5}，F={2,3,4}，H={2,3,4}。第2 组由540 个大型实例组成，其中，n={100,200}，m={5,10,20}，F={4,6,8}，H={30,40,50}。对于小型实例，每个组合都有5 个例子；对于大型实例，每个组合有 10 个例子[6]。

采用平均相对百分比偏差(ARPD)来评估算法的性能[7]，计算公式如下：

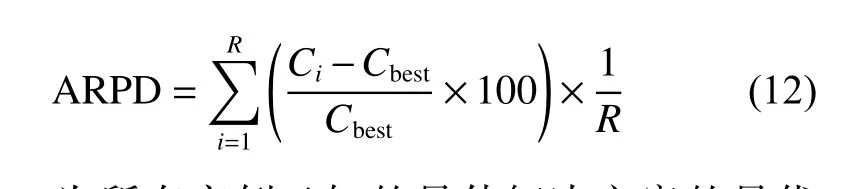
其中：Cbest为所有实例已知的最佳解决方案的最优值；Ci为算法每次运行后得到的最大完工时间的最小值，即算法的最优值，一共运行 R 次。如果ARPD＜0，则表明产生了新的最佳解决方案。所有实例的已知最优解都可在http://soa.iti.es 上获得。

4.1 参数设置

MBBO 算法有4 个关键参数：栖息地数量P（初始化产生的可行解的数量）、最大突变率mmax、最大迭代次数MaxIterations 以及退火率α。为了研究这4 个参数对MBBO 算法性能的影响，采用正交试验的方法对实例I_24_3_2_2_1 进行仿真计算。其中的“24”表示工件总数为 24，“3”表示每个工厂都有 3 台机器，第 1 个“2”表示一共有两个工厂，第 2 个“2”表示最终装配出两个产品，末尾的1 表示这个实例是这个组合的第1 个例子。表1 列出了影响算法性能的关键参数的不同组合。

图 6 MBBO 算法求解DAPFSP 问题的流程图Fig. 6 Flow chart of MBBO for solving DAPFSP

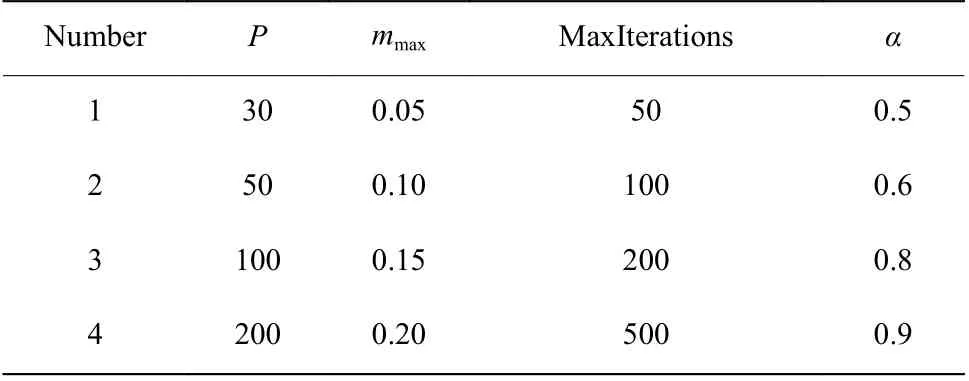
表 1 不同参数值的组合Table 1 Combination of different parameters

所有的参数组合都采用MBBO 算法运行10 次，计算平均最大完工时间(AM)，所得结果列于表2，由此观察不同参数对算法性能的影响，最终找出最令人满意的参数组合。

对于每个参数，将平均最大完工时间作为关键指标，判断每个参数的趋势，结果如图7 所示。

由图7 可以看出，栖息地数量和最大迭代次数越大，算法的性能越好，但同时计算成本会增加，时间明显变慢。综合考虑算法的性能效果以及耗费的时间成本，选取MBBO 算法参数如下：P=50，mmax=0.10，MaxIterations=100，α=0.9。此外，最大迁入率 I 和最大迁出率E 均设为1，取栖息地数量P 的10%作为保留的精英解。

4.2 模拟退火算法对MBBO 算法的影响

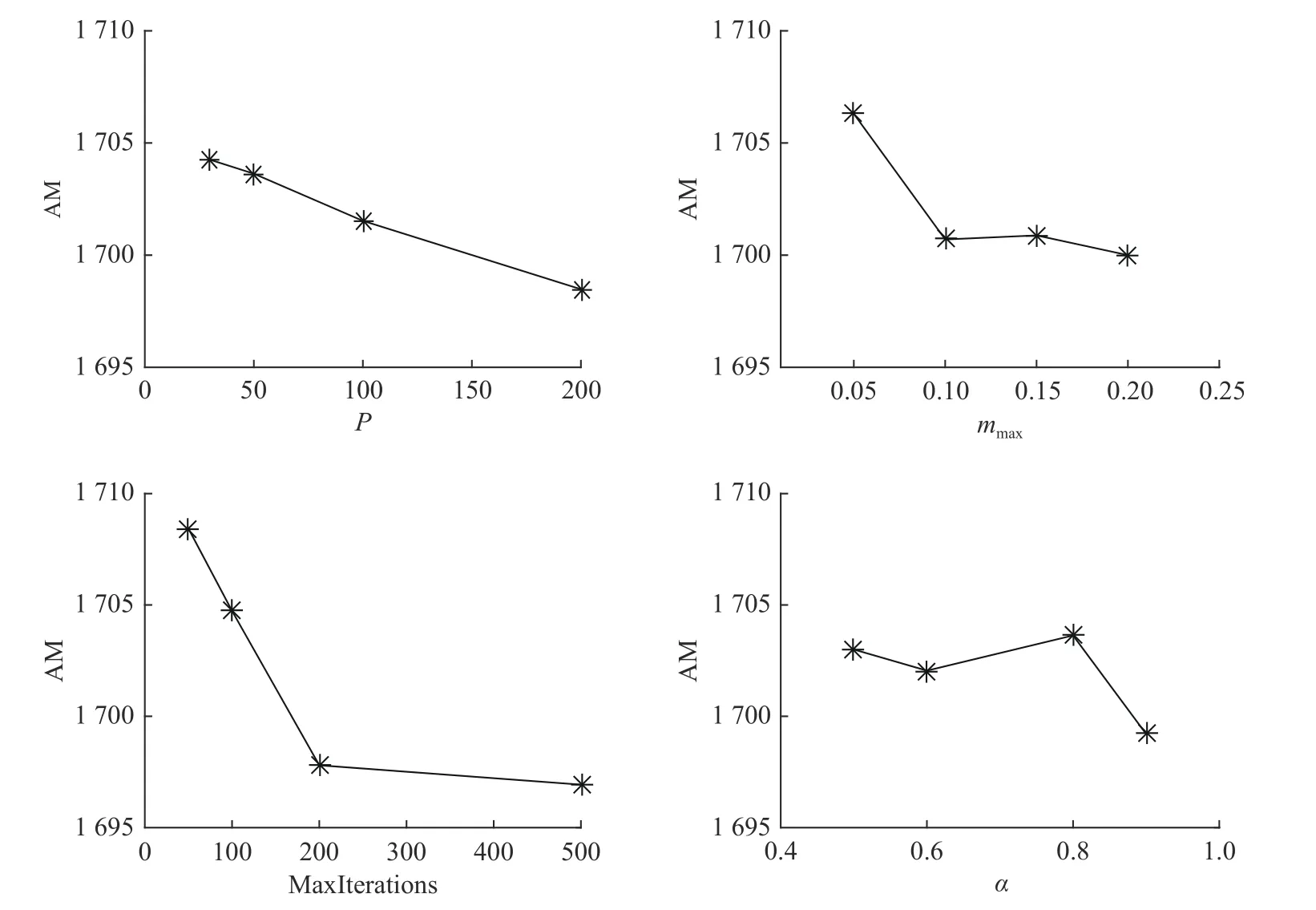
图 7 参数趋势图Fig. 7 Parameter trend chart

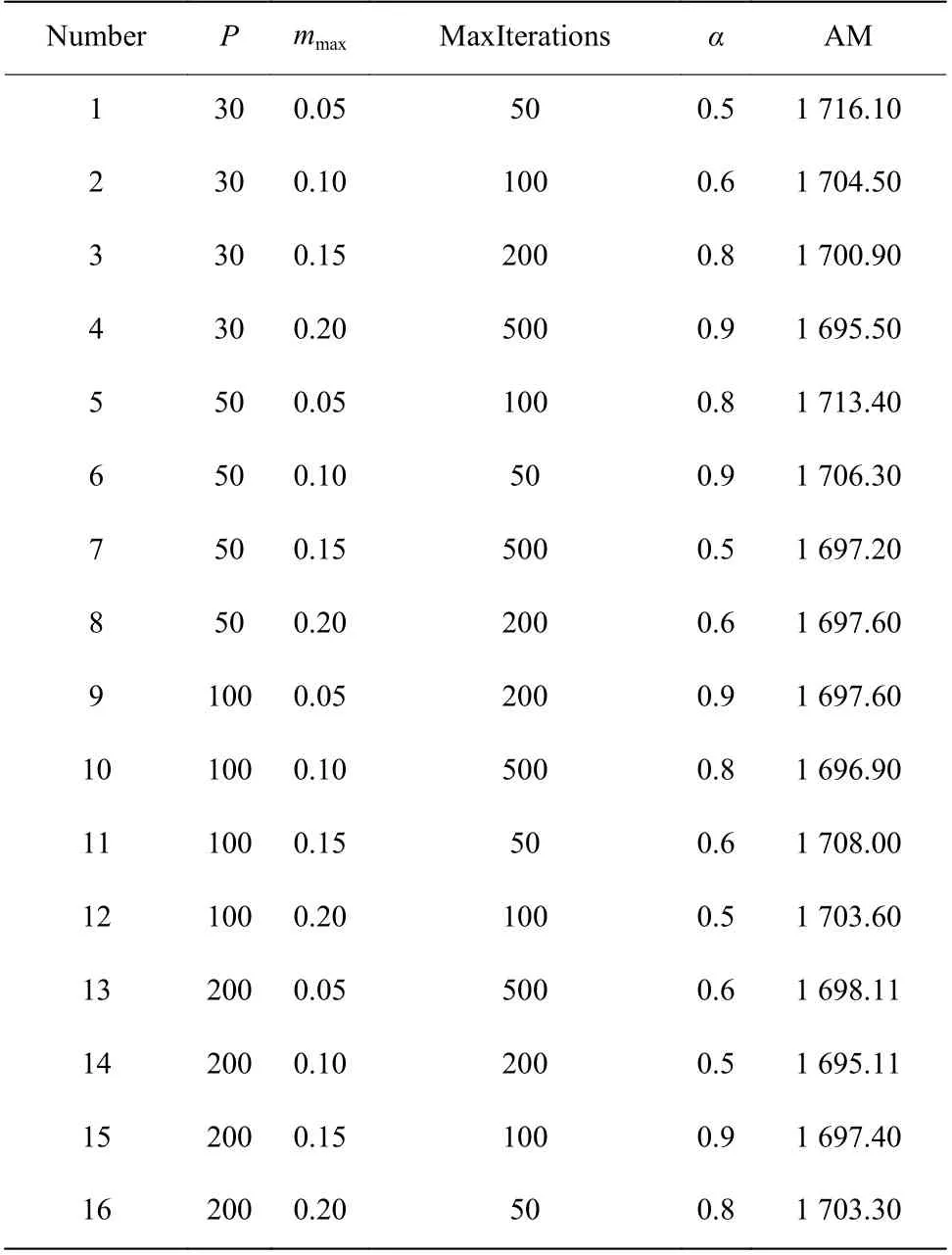
表 2 不同组合的平均最大完工时间Table 2 Average maximum completion time for different combinations

为了验证模拟退火算法对改进生物地理学优化算法的有效性，对所有小型实例进行仿真，比较了使用和不使用模拟退火算法的MBBO 算法的实例运算结果。两个算法都具有相同的参数设置（除了SA 算法的部分）和停止条件，并且独立运行5 次。表3 列出了F 和n 的15 个组合的平均ARPD 值，每个组合包含60 个小型实例。

模拟退火算法具有很强的全局搜索能力，能够使算法跳出局部最优而趋向于全局最优。从表3 可以看出，在大多数组合中，融合了模拟退火算法的MBBO 算法可以利用模拟退火算法的优势来获得较低的ARPD 值。不仅如此，MBBO 算法在有和没有模拟退火算法的情况下获得的ARPD 平均值分别为0.051 和0.100，前者的算法性能明显高于后者。由此可见，混合入模拟退火算法可以有效地改善所提出的MBBO 算法的性能。

4.3 DAPFSP 问题的小型实例

运用MBBO 算法求解分布式装配置换流水车间调度问题的900 个小型实例，每个实例都独立运行5 次，记录每次得到的算法最优值，利用ARPD 值评估算法的性能。表4 列出了F 和n 的15 种不同组合分组的统计结果，每个组合都包含60 个实例。取60 个实例的平均ARPD 值作为最终结果，并与H11、H12、 H21、 H22、 H31、 H32、 V NDH11、 V NDH12、 V NDH21、VNDH22、 V NDH31、 V NDH32算法进行比较。这 12 个算法都是用来解决DAPFSP 问题的有效方法，各算法的结果直接从文献中获得[5]。

表 3 MBBO 算法的小型实例运算结果Table 3 Small-sized instances results of MBBO algorithm

表 4 小型实例平均ARPD 值的结果对比Table 4 Comparison of average ARPD values of small-sized instances

从表4 可以看出，对于所有的小型实例，MBBO算法获得的结果明显优于12 个启发式与元启发式算法，且每个组合的平均ARPD 值和MBBO 算法的平均值均远远小于列出的12 个算法。不仅如此，MBBO 算法还更新了一些已知最佳方案，例如组合2×20 和 2×24 的 60 个实例的 ARPD平均值小于零。

本文还将MBBO 算法与BBO 算法的运算结果进行了比较。由于BBO 算法较为简单，运算速度快，因此对BBO 算法的参数进行如下调整：P=100，mmax=0.1，MaxIterations=200，I=E=1，取 P 的 10% 作为保留的精英解。由表4 可知，MBBO 算法求解DAPFSP问题的效率明显高于BBO 算法。在工厂数和工件数均较小的情况下（如 2×8 和 2×12），BBO 算法以初始栖息地和迭代次数多的优势，比MBBO 算法略胜一筹，但差别并不大。而当工厂数和工件数增大之后，BBO 算法便显出颓势，所得结果大不如MBBO 算法。所以，针对DAPFSP 问题，引入本文的3 种策略能有效地改善BBO 算法的性能，提高所得最优解的质量。

4.4 DAPFSP 问题的大型实例

针对分布式装配置换流水车间调度问题的540 个大型实例，同样运用MBBO 算法，将每个实例独立运行5 次，记录每次得到的算法最优值，利用ARPD 值评估算法的性能。表5 列出了工件数n=100和n=200 时的统计结果，每组都包含270 个实例，最终结果为每组所有实例的ARPD 平均值，然后与12 个启发式与元启发式算法以及BBO 算法的结果进行比较。

表 5 大型实例平均ARPD 值的结果对比Table 5 Comparison of average ARPD values of large-sized instances

由表 5 可以看出，当n=100 时，MBBO 算法有较大的优越性，其获得的大型实例的ARPD 平均值要远小于 H11、H12、H21、H22、H31、H32、 V NDH11、 V NDH12、VNDH21、 V NDH31这10 种算法的结果。当工件个数上升到 n=200 时，MBBO 算法获得的大型实例的ARPD 平均值均优于 H11、H12、H31、H32这 4 种启发式算法的结果，而比另外几种启发式和元启发式算法稍显不足。在大规模的实例中，与BBO 算法相比，MBBO 算法显然更为合理、高效，两个算法结果的平均值相差0.753，MBBO 算法优势显著。

综上所述，利用MBBO 算法求解DAPFSP 问题时，针对ARPD 平均值这个指标，在多数规模的实例上均效果良好，在某些实例上还找到了比已知方案更佳的结果。表6 列出了小型实例和大型实例中MBBO算法更新的最佳方案。MBBO 算法在初始化阶段利用SPT 规则、NR2规则和“虚拟工件”改良初始解，缩小算法搜索解空间的范围，提高搜索效率。在变异阶段，根据各工厂完工时间的信息，采用基于工厂完工时间的工件插入启发式方法，优化工件的工厂分配及加工顺序。同时，结合模拟退火算法，跳出局部最优，提高了算法的搜索能力。MBBO 算法是求解DAPFSP 问题的一种有效算法。

5 结束语

本文针对分布式装配置换流水车间调度问题，提出了一种改进的生物地理学优化算法及其应用于分布式装配置换流水车间调度问题的基本步骤，取得了较好的优化效果。针对BBO 算法的缺点，提出了3 种改进策略：使用SPT 规则和NR2规则初始化栖息地；在变异过程中加入基于工厂完工时间的工件插入启发式方法；加入模拟退火算法跳出局部最优。这3 种改进策略提高了算法的搜索能力，改善了算法的寻优效果。通过900 小型实例和540 个大型实例的仿真计算，并与12 个启发式与元启发式算法以及BBO 算法进行比较，验证了MBBO 算法求解DAPFSP 问题的有效性。

今后可以从以下几个方面做进一步的研究：

(1) 在迁移和变异操作过程中，MBBO 算法只是针对迁移和变异的方式进行改进，没有对其根本的

迁入率、迁出率和变异概率进行优化。可以考虑对迁移概率和变异概率的计算公式做出相应的改进，以提高算法的搜索能力。