基于直觉模糊VIKOR的水利项目评标决策研究

牛立军，王世洋

(华北水利水电大学 水利学院，河南 郑州 450046)

自我国招标投标法颁布实施以来,工程建设领域招投标竞争机制日趋完善,但在工程项目实际实施过程中,仍然存在着生产效率低下、质量差、安全环保意识不强等问题[1]。招投标工作作为工程项目启动的源头,其选择投标商的方法是否正确合理直接影响后期项目的建设质量。因此,建立科学、规范的工程项目评价方法并开展全面、客观的评价,对提高工程质量有着重要意义。

针对水利项目评标决策，许多国家以世界银行推行的最低评标价法选择投标商，即投标商在满足招标文件要求的条件下，将投标报价以外的因素价值量化，选择最低评标价作为中标方案。最低评标价法可以在一定程度上提高资金利用率，遏制暗箱操作现象，但可能会出现低价低质、索赔诉讼、成本超支等情况[2]。国内则普遍采用综合评估法选择投标商[3],综合评估法能够综合考虑投标商的企业状况、施工技术、管理水平、报价等定量定性指标,但对定性指标的量化问题,常受到专家主观偏好的影响,致使评价信息带有模糊不确定性。基于此,众多学者从不同角度展开研究,赵程伟等人引入Z-number模糊数处理定性指标量化问题,建立了基于Z-number理论的折衷排序工程评标模型[4]; 袁宏川等人将定性指标用三角模糊数表达,提出折衷模糊水电EPC项目评标决策方法[5]; 胡旸旸等人将格序理论引入水利项目评标决策,解决评标过程中的不可共度和矛盾性[6];于忠兰等人将组合赋权法和模糊综合评价应用到水电项目评标优化决策中[7]。

上述研究成果在一定程度上提高了评标结果的准确度,但仍有问题有待改进。一是专家的综合意见没有得到较好地处理。有些方法直接将专家意见简单平均综合,忽略了专家自身经验、偏好、专业范围等方面存在的差异,没有考虑专家自身权重对综合意见的影响。二是专家给予指标主观赋分之后,常常利用数学模型转化处理后再进行决策,这一过程可能会因评价信息的流失而造成评价结果偏离实际的情况。本文在前人研究的基础上,将直觉模糊集理论应用到水利项目评标决策中,充分考虑指标隶属度、非隶属度和犹豫度方面的信息,从指标层面入手,依据熵理论确定每个专家赋予的指标权重和专家自身权重,建立最小偏差优化模型确定指标综合权重,以此解决专家在评价过程中的模糊不确定性和意见综合问题,结合VIKOR方法对投标商进行排序,合理选出符合工程实际和自身需求的投标商,确保工程如期、高质量完成。

一、构建评标指标体系

构建系统完整的评标指标体系是选择合适投标商的关键。随着水利工程建设的不断推进,评标指标也进行了相应的优化,业主在注重传统评标指标的同时,对新技术、新工艺、新材料等应用也给予了高度的重视。因此,为体现新形势下“高质量”的建设理念,构建完善的指标体系需考虑以下原则:一是投标商应具备良好的企业状况;二是投标商应具有优越的施工技术和管理能力;三是投标商应配置充足的装备和人员;四是投标商应具备强有力的服务保障和强大的风险应对能力。根据这些原则并结合已有文献,建立水利项目评标指标体系，见表1。

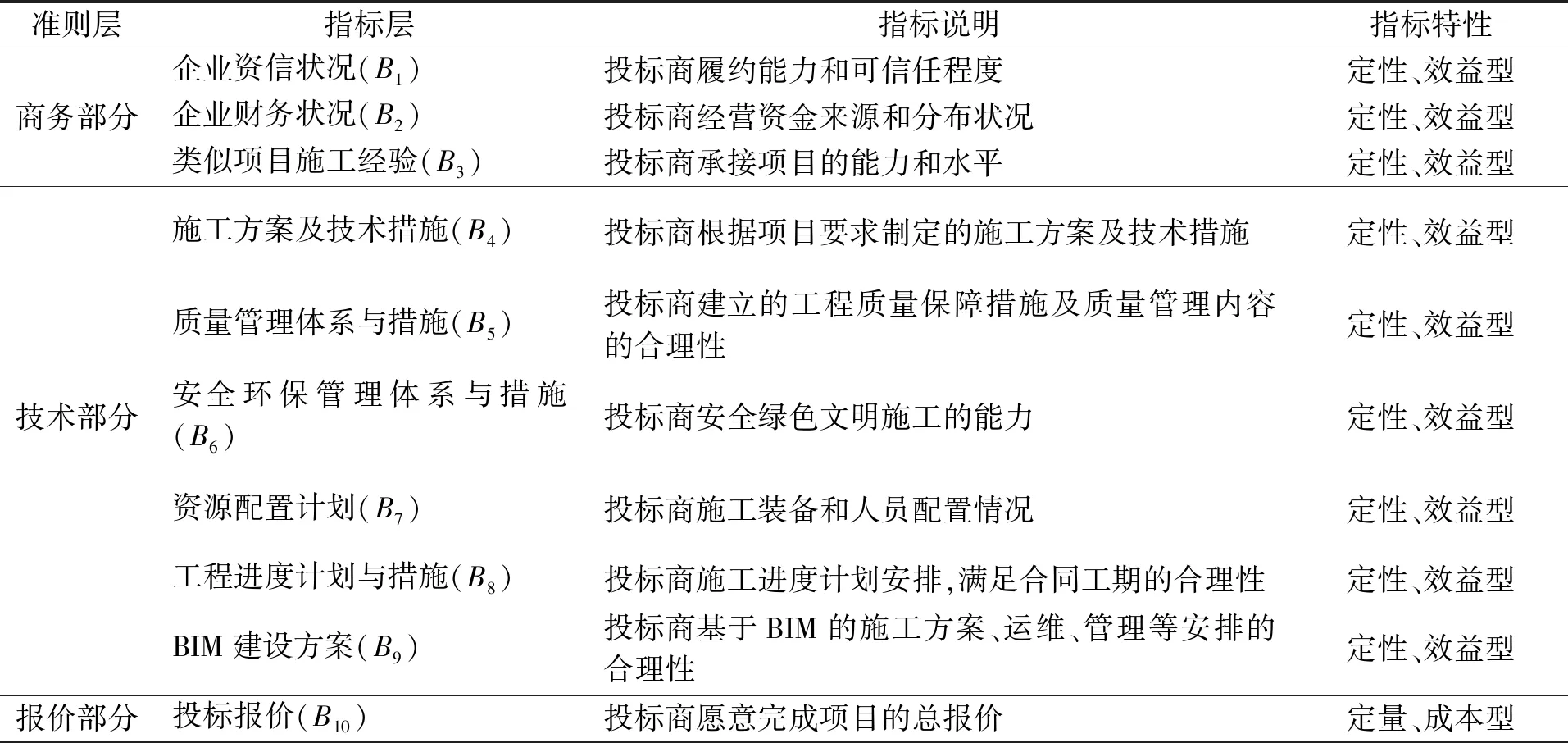
表1 水利项目评标指标体系

二、建立水利项目评标决策模型

(一)直觉模糊集

设X为给定集合,则称

A={|x∈X}

为属于X的直觉模糊集。其中,μA(x),νA(x)分别表示X中元素x属于A的隶属度(满足程度)和非隶属度(不满足程度),且满足条件

0≤μA(x)+νA(x)≤1,x∈X。

此外,称πA(x)=1-μA(x)-νA(x)表示一个问题的犹豫度或不确定程度[8]。为描述方便,将直觉模糊数记为(μA(x),νA(x))。

设A、B是X上的任意两个直觉模糊数,两者之间的欧式距离[9]为

(1)

(二)规范化指标评价信息

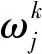
水利项目评标决策的指标体系具有混合特性,由定量和定性两类指标组成,各指标不可以用同一单位衡量,即存在不可公度性。为了使评标结果更加准确可靠,本文对定量和定性指标的评价信息统一用直觉模糊数表示,以避免群决策信息的流失。定量指标(投标报价)的处理直接将投标商的报价得分作为隶属度,得分标准以报价与基准价的偏差率为基础,报价每高于或低于基准价一个百分点扣除相应的分数,最后得分记为xij,反映了投标商的报价对所投项目的满足程度(隶属度),将其表示为直觉模糊数,即

(2)

定性指标常用好、一般、差等模糊性语言来描述偏好信息[10],为便于评价，这些模糊性语言信息需要转化为具体的数值。本文采用7个语言评价粒度来描述语言变量评价信息,对应的直觉模糊数见表2。

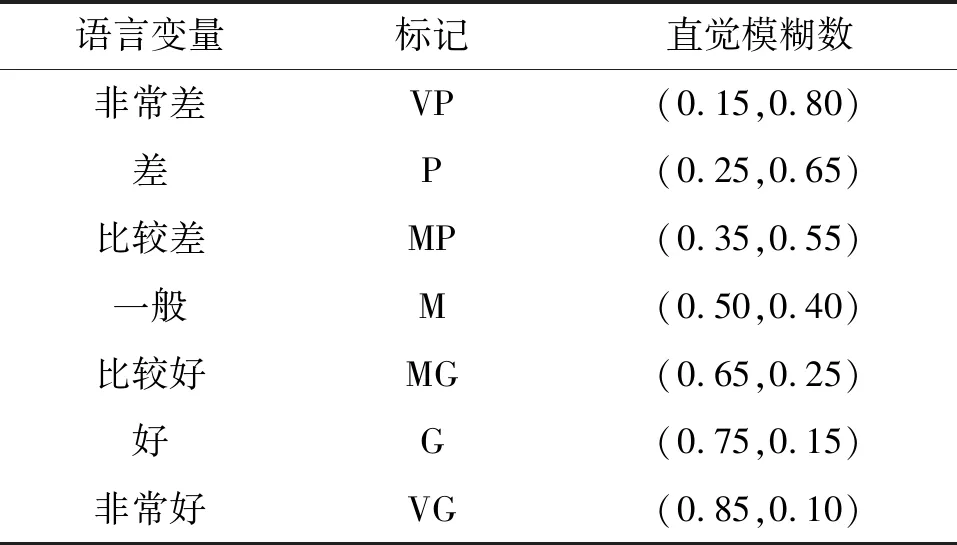
表2 定性指标评价语言与直觉模糊数的转化关系

将分值和语言评价信息统一转化为直觉模糊数形式,得到专家Ck的直觉模糊评价矩阵

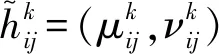
(三)确定指标权重

利用直觉模糊熵的大小来反映专家对指标评价信息的模糊不确定程度,直觉模糊熵越大,说明专家给出的评价信息模糊不确定程度越高,应分配指标较小的权重,反之,则分配较大的权重。专家Ck对指标Bj评价的直觉模糊熵[11]为

(3)

则专家Ck直觉模糊评价矩阵确定的指标权重可表示为

(4)

指标综合权重可通过建立最小偏差优化模型[12]确定。

(5)

其次,检验左右端点是否为奇异权重,具体做法是以dj/2为半径,判断左右端点的邻域

和

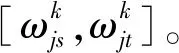
(6)

(四)确定专家权重

我国《招标投标法》规定,依法必须招标的项目,评标专家由5人以上单数组成(1)《中华人民共和国民法通则》第一百五十五条规定“以上”“以下”“以内”包括本数。《招标投标法》属于民法范畴，故本文选取专家人数为5人。。而各专家的专业范围、认知水平等不尽相同,故需要合理分配专家权重。专家权重分配取决于所给出评价信息的精确可靠程度,专家给出的评价信息越精确可靠,说明专家对判断对象的了解程度或掌握的信息越多,应分配较大的权重,反之,则分配较小的权重。依据熵理论和加权直觉模糊熵确定专家权重

(7)

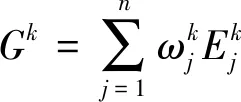
(五)VIKOR方法折衷排序

VIKOR(多准则妥协解排序)方法是一种基于理想点、折衷排序的多准则决策方法[13],其特点是能够同时考虑最大的群体效用和最小的个人遗憾,以最贴近理想解的思想对选择方案折衷排序。

1.利用直觉模糊加权平均算子将各专家决策矩阵集结成群决策矩阵,即

(8)

2.依据群决策矩阵,确定各指标下的正理想解和负理想解,即

(9)

(10)

式中，E为效益型指标集合，F为成本型指标集合。

3.采用VIKOR方法分别计算各投标商的群体效用值S(Ai)、个人遗憾值R(Ai)、折衷评价值Q(Ai),即

(11)

(12)

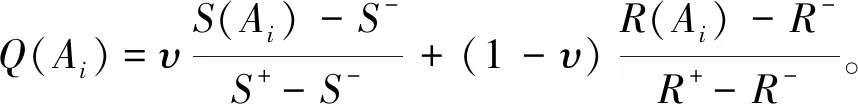
(13)

式中：d为任意两直觉模糊数之间的欧式距离；S+=max[S(Ai)]，S-=min[S(Ai)]，R+=max[R(Ai)]，R-=min[R(Ai)]；1≤i≤m；υ为折衷系数,υ∈[0，1]，当υ>0.5时,表示偏向最大化群体效用进行决策,当υ=0.5时,表示均衡最大化群体效用和最小化个人遗憾进行折衷决策，当υ<0.5时，表示偏向最小化个人遗憾进行决策。本文υ取0.5。

根据S(Ai)、R(Ai)及Q(Ai)的值对投标商进行优劣排序,如果投标商Ai的Q(Ai)值为最小值且同时满足以下两个条件,则Ai为评标决策的最优投标商。

条件一Q2-Q1≥1/(m-1),式中Q1和Q2分别对应Q(Ai)值排序中的最小值和次小值,m为备选投标商数量,当m≤4时,1/(m-1)取0.25。

条件二最优投标商Ai在S(Ai)值和R(Ai)值排序中均为最小值。

若仅满足条件一,则说明所有投标商均接近于理想解;若仅满足条件二,则说明Q1和Q2所对应投标商均为折衷解。

三、算例验证

某水利项目面向社会公开招标,共有4家投标商(A1,A2,A3,A4)通过审查,投标报价依次为:985万、974万、986万、972万,特邀请5位专家依据评价指标分别对4家投标商进行评价,利用本文提出的评标决策模型对投标商进行排序。具体步骤如下:

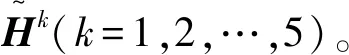
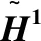
表3 规范化直觉模糊评价矩阵

步骤2利用式(3)—(6)计算不同专家分配的指标权重和综合权重。由表3计算出专家C1分配的指标权重

ω1=(0.087 0.076 0.100 0.076 0.073 0.073 0.070 0.084 0.076 0.285)。

相同的方法可求出专家C2、C3、C4、C5分配的指标权重

ω2=(0.098 0.087 0.062 0.062 0.076 0.112 0.087 0.101 0.067 0.249)，

ω3=(0.076 0.091 0.079 0.091 0.079 0.067 0.079 0.117 0.064 0.259)，

ω4=(0.083 0.073 0.108 0.108 0.097 0.070 0.073 0.073 0.077 0.239)，

ω5=(0.113 0.110 0.082 0.074 0.074 0.069 0.069 0.059 0.071 0.279)。

则评价指标综合权重

ω*=(0.093 0.084 0.088 0.084 0.078 0.072 0.077 0.088 0.073 0.264)。

步骤3基于评标决策模型所提出的专家权重确定方法,利用式(7)依次计算出各评标专家的权重，λ1=0.194,λ2=0.204,λ3=0.200,λ4=0.205,λ5=0.198。

步骤4利用式(8)将各专家决策矩阵集结成群决策矩阵，见表4。

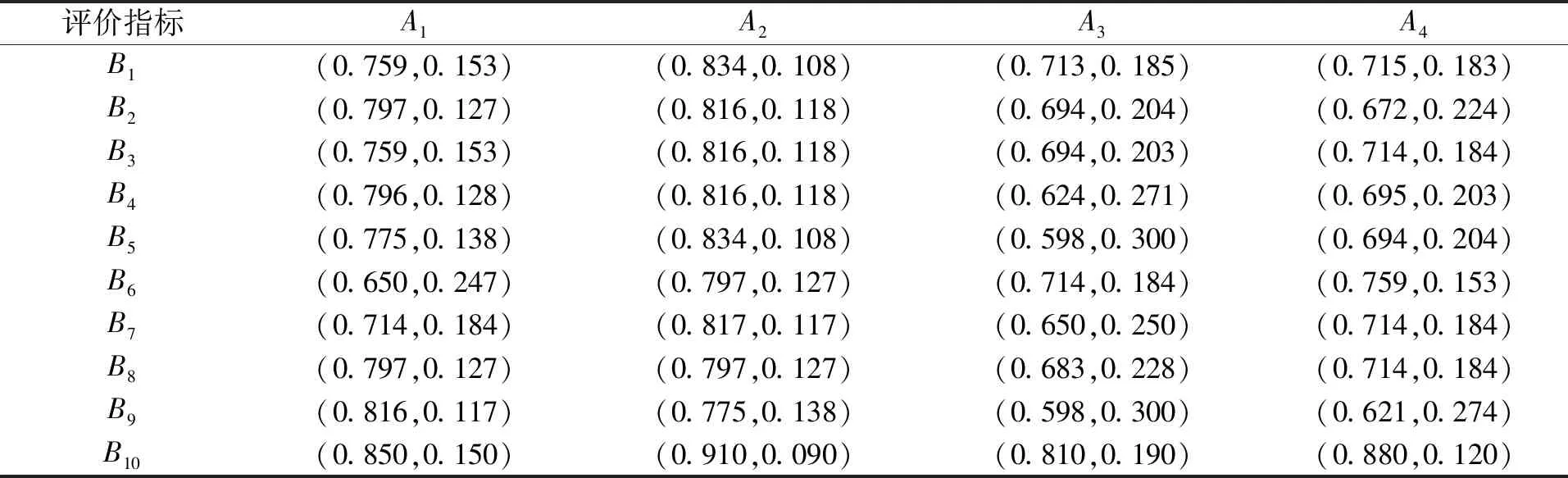
表4 群决策矩阵F

步骤5根据群决策矩阵F,确定投标商各指标下的正理想解和负理想解分别为

f+=(0.834,0.108),(0.816,0.118),(0.816,0.118),(0.816,0.118),(0.834,0.108),

(0.797,0.127),(0.817,0.117),(0.797,0.127),(0.816,0.117),(0.910,0.090);

f-=(0.713,0.185),(0.672,0.224),(0.694,0.203),(0.624,0.271),(0.598,0.300),

(0.650,0.247),(0.650,0.250),(0.683,0.228),(0.598,0.300),(0.810,0.190)。

步骤6根据直觉模糊欧式距离测度公式及式(11)—(13)计算各投标商群体效用值S(Ai)、个体遗憾值R(Ai)和折衷值Q(Ai),排序结果见表5。

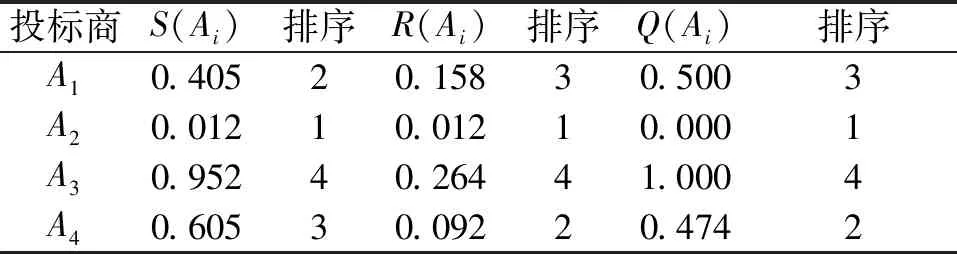
表5 各投标商的S(Ai)、R(Ai)及Q(Ai)值排序

由表5可以看出,依据折衷值Q(Ai)的大小进行优劣排序的结果为A2≻A4≻A1≻A3,其中Q(A4)和Q(A2)的差为0.474，大于0.25,满足条件一；同时,A2在S(Ai)值和R(Ai)值中均为最小值,满足条件二。因此,A2为此次项目评标的最优投标商。

四、敏感分析

(一)对比分析

使用熵权-TOPSIS方法的计算结果见表6。

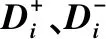
表6 各投标商的及Ti值

由表6可以看出，各投标商优劣排序结果为A2≻A1≻A4≻A3，与VIKOR方法得到的最优投标商均为A2，两种方法都可以达到对投标商择优的目的，相比之下，投标商A1和A4的排序发生了变化。引起差异的主要原因是熵权-TOPSIS方法对定性指标的评价值带有主观随意性，忽略了专家认知过程及结果的不确定因素。此外，TOPSIS方法是以距离正理想解最近，且距离负理想解最远进行排序，没有考虑两个理想点之间的关联性，最终评标结果不一定最接近理想解。本文所提决策方法可以有效解决专家评价过程中以及结果的不确定因素，考虑直觉模糊评价值到正、负理想解的距离以及两理想点之间的距离，以折衷解的方式进行排序，进一步客观选择最优投标商。

(二)敏感性分析

在使用VIKOR方法进行选优排序时,因其带有参数υ,且参数的取值对决策结果有一定的影响,故需要对参数折衷系数υ进行敏感性分析,以体现该方法的可靠性和稳定性,具体是在υ∈[0,1]中按照0.1的步长计算不同折衷系数υ对决策结果的影响,如图1所示。

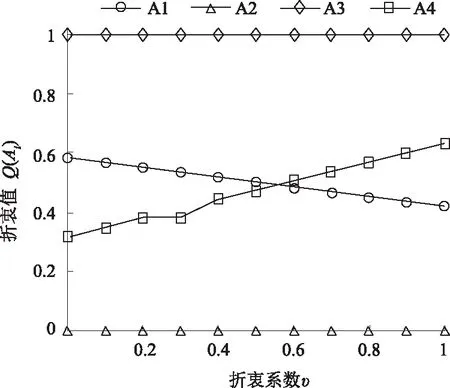
图1 折衷值Q(Ai)随折衷系数υ的变化情况

由图1可以看出,投标商A2和投标商A3的Q(Ai)值不随折衷系数υ的改变而发生变化,投标商A2的排序结果始终为最优，投标商A3始终为最劣；投标商A1和投标商A4的排序随折衷系数υ的变化而发生了变化,这说明本文所提出的评标决策方法能够依据专家主观偏好信息获得不同的排序结果。此外,投标商A2在υ∈[0,1]中任意取值均满足条件一和条件二,因此,投标商A2在评标决策过程中是可靠稳定的最优投标商。

五、结语

本文在构建新形势下水利项目评标指标体系的基础上,提出了一种基于直觉模糊和VIKOR

相结合的评标决策方法。整个评标决策过程的评价信息始终以直觉模糊数表示,避免了评标过程中群决策信息流失的问题,有效削减了专家判断过程中的模糊不确定性,依据直觉模糊熵理论确定指标权重和专家权重,合理确定指标综合权重,综合考虑了各专家的意见,评标结果更加客观。通过水利项目实例使用VIKOR方法进行排序并结合敏感性分析,验证了该评标决策方法的可靠稳定性。