基于广义柔度曲率信息熵的梁结构损伤识别方法

项长生，李凌云，周 宇，王立宪，吴 侃

(1. 兰州理工大学土木工程学院，甘肃 兰州 730050； 2. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心，甘肃 兰州 730050； 3. 安徽建筑大学土木工程学院，安徽 合肥 230601)

0 引言

梁结构在服役过程中会因为材料性能退化、 承担荷载变化等因素出现不同损伤，存在潜在的安全隐患，对其进行及时有效的健康监测与损伤诊断具有非常重要的意义[1]. 因此，学者们对梁结构的损伤识别方法展开了广泛且深入的研究，其中，柔度矩阵包含了结构固有频率和模态振型这两种结构动力特性，广泛用于结构的损伤识别[2-5]，如柔度曲率[6-7]、 柔度曲率差变化率[8]等. 为了克服柔度矩阵在结构损伤定位上存在的缺陷，文献[9-10]首次将结构损伤前后的广义柔度矩阵(generalized flexibility matrix, GFM)的变化用于识别结构损伤，表明GFM具有较好的损伤定位能力. 由于广义柔度矩阵引入了高次频率，从而有效减小了截断高阶模态造成的截断误差的影响. 因此，一经提出就受到广大学者的关注[11-14].

信息熵可以度量系统中某个信号所提供信息量的无序程度，对系统的非线性具有显著的突显作用. 在机械故障诊断[15-16]和图像处理[17-18]等领域得到广泛应用. 但在混凝土梁式结构的损伤识别方面的相关研究并不多见，具有较大的发展潜力. 文献[19]首次系统地将信息熵理论应用到混凝土结构损伤识别中，用信息熵来描述结构单元能量分布的均匀程度(主要体现在单元刚度和频率带的变化上). 随后，有学者将信息熵理论用于混凝土结构的裂缝扩展及损伤演化的研究中, 取得了较好的研究成果[20-22].

本研究结合信息熵和广义柔度矩阵在结构损伤识别中的优势，提出广义柔度曲率信息熵指标(generalized flexibility curvature information entropy, GFCIE)，以简支梁和连续梁这两种常见梁结构为例，对新指标的有效性进行验证.

1 广义柔度曲率矩阵

设M为n×n阶与归一化振型{Φi}相关的结构质量矩阵，且满足正交条件：

{Φi}TM{Φi}=1

(1)

基于对振型归一化的质量矩阵，广义柔度矩阵定义为[9]：

Fg=F(MF)l=ΦΛ-1ΦT(MΦΛ-1ΦT)l=ΦΛ-1-lΦT(l=0, 1, 2, …)

(2)

(3)

式中:ωi为第i阶振动圆频率;δi为第i阶归一化系数;n为模态阶数. 本研究只考虑l=1的情况，此时广义柔度矩阵表达式为：

(4)

对GFM做一次横向差分，可以得到一个(n-2)×n阶矩阵dFg：

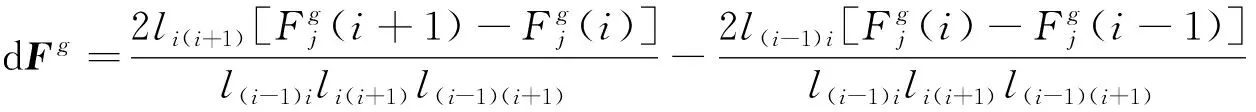
(5)

(6)

由于广义柔度曲率矩阵是一个(n-2)×(n-2)矩阵，会造成边跨支座处节点信息的缺失，这是其不可避免的缺点，应该引起注意.

2 GFCIE指标的提出与计算

2.1 信息熵的基本理论

熵是热力学和统计物理学中特有的宏观量，1948年信息论的创始人香农(Shannon)打破学科壁垒，创造性地提出了信息熵的概念：

(7)

式中:S为某个信息所携带信息量的大小，反应信号状态的紊乱程度；pi是第i种信源信号出现的概率； lnpi是第i种信源信号的自信息量.

2.2 构造GFCIE指标

提取广义柔度曲率矩阵ddFg的对角线元素，并按节点顺序组成一个列向量，将其定义为广义柔度曲率矩阵的对角向量Π：

Π=diag(ddFg)

(8)

将广义柔度曲率对角线元素占总对角线元素之和的比值定义为GFCIE指标函数中的概率函数P(x)：

(9)

显然，新引入的物理量P(xi)满足完备性和非负性，即：

(10)

将式(9)代入式(7)中可得广义柔度曲率信息熵的表达式：

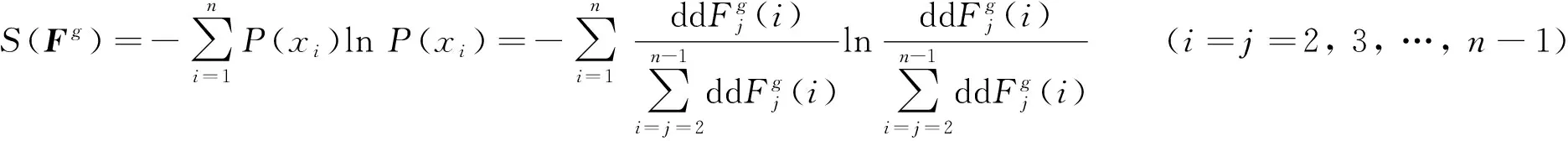
(11)

广义柔度曲率信息熵指标以广义柔度矩阵对结构损伤的敏感性为切入点，以概率的形式对结构出现损伤的分布状态及发展程度进行描述，其计算的具体步骤如下.

1) 对结构进行损伤前后的模态分析，提取结构的模态数据，根据公式(4)～(6)编制MATLAB程序计算结构广义柔度曲率矩阵ddFg，并提取其对角线元素构造对角向量Π.

2) 再将广义柔度曲率对角线元素占总对角线元素的比值作为GFCIE指标函数中的概率函数P(x)，由公式(7)～(11)计算结构的GFCIE指标.

3 算例验证

3.1 简支梁损伤识别

用MIDAS/Civil建立一等截面简支梁，梁计算跨径为6 m，截面尺寸为0.4 m×0.2 m，主梁材料采用C50混凝土，混凝土的弹性模量E=34.5 GPa，泊松比μ=0.2，容重c=25 kN·m-3，质量密度ρ=2.549 kN·(m3·g)-1. 将结构均匀划分成50个单元, 假设结构损伤只表现为结构刚度的减小，而质量矩阵保持不变[24]，如图1所示.

图1 简支梁单元划分和截面尺寸 (单位：m)Fig.1 Element distribution of simply supported beam and section size (unit: m)

本研究提取结构第一阶固有频率和模态振型，根据GFCIE指标的计算步骤，简支梁的损伤工况识别结果如图2～3所示. 由图2可知，GFCIE指标显示出了较好的定位能力，与表1中设定的简支梁损伤工况比较吻合. 可以看到，跨中位置不同程度的损伤指标突变峰值层次分明，可起到预判结构相对损伤程度的作用. 对支座附近的识别结果不尽人意，虽能定位损伤，但指标突变规律无迹可寻.

图2 工况1～3损伤识别结果Fig.2 Case 1 to 3 damage identification results

图3 工况4～6损伤识别结果Fig.3 Case 4 to 6 damage identification results

表1 简支梁损伤工况Tab.1 Damage cases of simply supported beam

对于多处损伤工况，GFCIE指标也展现出了令人满意的损伤定位能力. 如图3所示，除了支座处的3号单元外，16、 30和45号单元的GFCIE指标都随着损伤的扩展而持续增大. 工况4中，四处损伤位置都设定了20%的损伤，在图3中对应的指标最大突变值分别为：0.004 6、 0.018、 0.019和0.023，除了3号单元外其他三个单元的指标值较为接近，即可以通过指标突变值反应结构各损伤量的接近程度.

3.2 连续梁桥损伤识别

以两跨钢筋混凝土连续梁桥为例，验证所提GFCIE指标对不同梁结构的适用性. 结构材料与3.1节简支梁的材料相同，全桥均匀划分为40个单元. 对连续梁定义了单处损伤、 对称位置损伤和多位置损伤这三种损伤工况，在识别损伤时根据ΔS(Fg)突变量的大小定性判断结构的损伤程度，具体工况如表2所示. 桥全长40 m，跨径布置为20 m+20 m，主梁截面形式为单箱单室箱型，如图4所示.

表2 连续梁损伤工况Tab.2 Damage casesof continuous beam

(a) 单元划分 (b) 截面尺寸图4 结构单元划分和截面尺寸 (单位：cm)Fig.4 Element distribution of structural and section size (unit: cm)

识别结构损伤时，在损伤处y轴的正上方会有突变, 各损伤工况的识别结果如图5～10所示. 由图5可知，结构发生单处损伤时，在3号单元处出现了突变，这与工况7设定的损伤位置相同. 注意到，在没有设定损伤的位置处也出现了不同程度的突变，这可能是由指标构造过程中模态数据多次迭代引起的，但其突变量较小，不影响指标对结构损伤识别结果的准确性. 对比不同损伤程度的突变值，当损伤程度从10%增大到50%时，指标最大突变值分别为：0.013、 0.038、 0.061、 0.098、 0.151，将结构损伤程度与其对应单元的GFCIE指标最大突变值的变化关系进行拟合，如图6所示. 发现GFCIE指标在损伤位置的突变量随着损伤程度的增加呈现出线性增加的趋势，在损伤程度大于40%时，指标突变的增幅迅速上升，可以推断损伤位置处的结构部件已进入塑性破坏阶段.

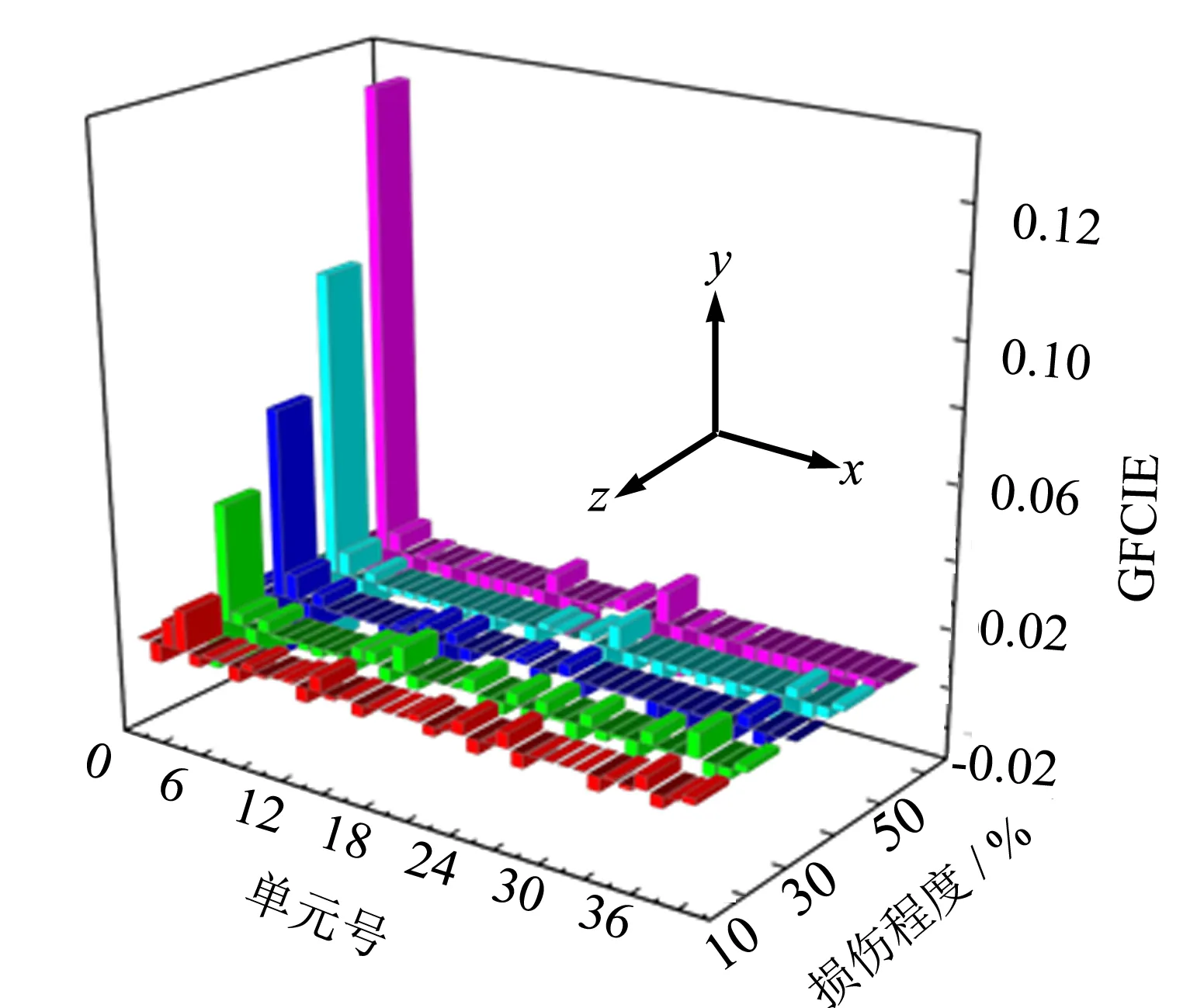
图5 工况7损伤识别结果Fig.5 Case7 damage identification results

图6 工况7损伤拟合曲线Fig.6 Case7 damage fitting curve

工况7损伤拟合曲线方程为：

y=3.33x4-2.7x3+0.99x2-0.065x-0.000 17

(12)

算例所示连续梁为对称结构，其普遍存在对称位置损伤识别出现异常的问题，遂对指标用于结构对称位置的损伤工况的实用性进行研究.

工况8中为10号单元和30号单元同时发生10%、 20%、 30%的损伤，损伤识别结果如图7所示. 可以清楚地看到，在10、 11、 30、 31号节点处的指标突变值明显大于其他位置的突变值，且两组对称节点的突变值比较接近，如10、 30号单元均发生20%的损伤时，对应节点的指标最大突变量分别为0.018和0.020. 由图8可知，结构两边对称位置发生不同程度的损伤时，GFCIE指标峰值的位置也随之变化. 当10号单元和30号单元分别发生20%和40%的损伤时，对应节点的损伤指标最大突变量分别为0.026和0.059. 那么，GFCIE指标完全可以胜任对称结构的损伤识别，且损伤识别结果比较理想.

图7 工况8损伤识别结果Fig.7 Case 8 damage identification results

图8 工况9损伤识别结果Fig.8 Case 9 damage identification results

3.3 GFCIE指标抗噪性分析

工程中，实测模态信息难免会受到各种噪声与误差的干扰，如噪声引起的测量误差、 测量仪器自身的误差、 温差影响等. 理论上认为误差的变化服从高斯分布[25]，但高斯分布与实际误差的有界性相矛盾. 今引入服从截尾高斯分布 (truncated gaussian distribution, TGD) 的误差模型[26], 将服从高斯分布的随机变量模型进行截尾修正. 模拟误差以式(13)～(14)的形式引入：

(13)

(14)

对工况8分别引入噪声水平为3%、 6%、 10%和12%的误差，损伤识别结果如图9所示. 由图9分析可知，当噪声水平不大于10%时，GFCIE指标可以较好地定位损伤位置，定性判断结构相对损伤程度. 当噪声水平超过10%时，损伤程度为10%的损伤工况无法通过GFCIE指标正确识别，损伤程度为20%和30%的损伤，仅可通过指标突变最大值及局部刚度退化情况描述其损伤位置和损伤程度.

(a) 引入3%噪声损伤识别结果

(b) 引入6%噪声损伤识别结

(c) 引入10%噪声损伤识别结果

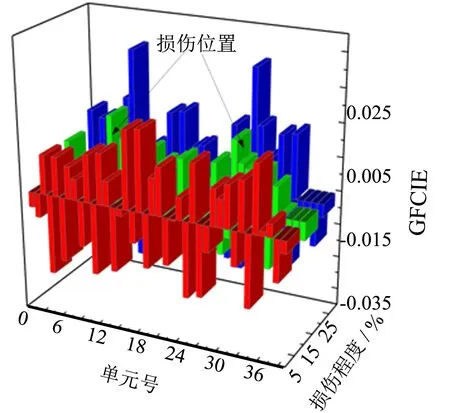
(d) 引入12%噪声损伤识别结果图9 GFCIE抗噪性分析Fig.9 Anti-noisy analysis of generalized flexibility curvature information entropy

4 结语

结合信息熵与广义柔度矩阵在结构损伤识别中的优势，提出了基于广义柔度曲率信息熵指标的结构损伤识别方法，用MIDAS/Civil建立简支梁和连续梁两种不同的梁结构验证了指标的有效性，并采用截尾高斯误差模型验证了所提指标的抗噪性，得到以下结论.

1) 相对于普通柔度矩阵，广义柔度矩阵可进一步降低高阶模态的贡献，提高指标识别精度. 但在广义柔度曲率矩阵推导过程中会损失结构两端2个节点的模态信息，会对支座处的损伤识别造成影响.

2) 所提GFCIE指标可以胜任不同类型的梁结构损伤识别，仅用一阶模态数据就可较好地识别结构的单处、 对称位置处、 多处损伤的位置，且能定性反应其损伤程度. 在识别过程中存在未损伤单元处也出现了突变，尤其在GFCIE指标轴负方向出现较大突变的问题，虽不影响结构损伤的判断结果，但仍值得注意，这也是接下来需要改进的地方. GFCIE指标对实际结构工程的损伤识别能力还需进一步验证提升.

3) 采用服从截尾高斯分布的误差分布模型对指标的抗噪性能进行分析，该方法相比普通高斯误差分布模型实际更接近误差分布. 结果表明，GFCIE指标具有一定的抗噪能力，但对噪声水平在10%以上的抗噪能力有待进一步完善提升.