基于分子动力学的正十八烷/石墨层吸附行为分析

张田田 陈振乾

(东南大学能源与环境学院，南京 210096)

相变材料是一类具有储能和释能特性的功能性材料.最常见的储能方式有显热储能、潜热储能和化学储能.其中，潜热储能是基于材料在相变过程中的吸热或释热[1]，这种储能方法与显热储能相比，具有更高的储能密度.潜热储能通常按其相变行为分为固-气、气-液和固-液3大类[1-2].对于固-气和气-液相变材料，由于其在相变过程中巨大的体积变化而未被广泛应用.常见的固-液相变材料虽然相变过程中体积变化较小，但也存在热导率低、相变时发生泄漏等固有缺点[3-4].烷烃类有机材料作为一种广泛使用的相变材料，具有较广的熔化温度、中等的储热密度(200 kJ/kg)、较高的熔解潜热以及理想的热稳定性和化学稳定性[5].

为了防止该类材料相变时发生泄漏，同时提高材料的导热性能[6]，人们通过复合其他高导热材料来制作定型相变材料[7-8].目前，多孔碳材料如膨胀石墨、石墨泡沫和碳纳米管等已得到应用，Zhong等[9]、Lafdi等[10]和Li等[11]研究了石蜡-石墨泡沫复合相变材料储能系统的结构、热扩散率和潜热等性能，发现与导热率为0.25 W/(m·K)的纯石蜡相比，不同泡沫石墨掺杂量的石蜡-泡沫石墨复合相变材料的导热率分别可提高190倍、270倍、500倍和570倍.Xiang等[12]研究发现在石蜡材料中添加剥离石墨纳米片后，该石蜡基复合相变材料的导热性得到较好改善，同时剥离石墨纳米片使得石蜡的潜热略有提高.

其中，烷烃和多孔碳材料组成的定型相变材料具有良好的导热性，无毒、环保，还可加工成不同的形态，其在动力电池热管理系统中的应用已成为相变材料的研究热点[13-14].Cheng等[15]制备的膨胀石墨/石蜡复合材料轻质墙体具有良好的导热性能，通过添加质量分数20%的膨胀石墨，使复合相变材料的导热系数提高至0.76 W/(m·K).

为了解多孔碳材料对烷烃相变材料作用的微观机理，分子动力学(MD)方法可作为宏观实验的补充.Luo等[16]采用分子动力学方法研究了石蜡/膨胀石墨复合相变材料的传热性能；Liu等[17-18]和Feng等[19]利用分子动力学方法研究了石蜡和聚苯乙烯/铜表面混合物的蓄热和导热性能.基于此，本文采用数值模拟方法，通过构建石墨层与正十八烷(C18H38)分子的复合相变材料模型，从微观尺度研究正十八烷分子的排布、自扩散系数以及分子间的结合强度等参量，探讨石墨层的添加对正十八烷相变材料储热性能的影响机理.

1 模型及方法

1.1 模型构建

本文建立了2种相变材料(PCM)模型，包括石墨层/正十八烷复合相变材料模型和纯正十八烷模型，如图1所示.

(a) 石墨层/正十八烷复合相变材料模型

(b) 纯正十八烷模型

以正十八烷为相变材料、石墨层为支撑材料，建立了由石墨层和2层石蜡(正十八烷)组成、共有9 744个原子的“三明治”复合相变材料微观模型.为了保证结构的分子排列合理，首先对体系进行几何优化，然后在正则系综(NVT)下，在253～333 K的温度范围内每间隔10 K进行1 ns的退火，以获得可用于动力学计算的稳定初始构型.随后，将上述能量最小化的构型在等温等压系综(NPT)下进行动力学模拟，每个模拟总长为3 ns，时间步长选为1 fs，弛豫时间确定为1 ns，截断距离为1.25 nm.

1.2 分析方法

为描述正十八烷与石墨层间相互作用，本文通过分子动力学模拟，使用凝聚相优化分子势力场(COMPASS)[20]，采用Lennard-Jones(L-J)势函数来描述体系中非键相互作用.其中运动方程的求解采用Velocity Verlert 算法[21]，其优点在于每步仅需评估一次能量，且允许使用相对较大的时间步长.

1.2.1 自扩散系数

自扩散系数[22]是一种重要的热物理性质，可以表征传质现象，从而指导材料的微观设计.均方位移(mean square displacement, MSD)[23]是用模拟时间计算原子轨迹的统计平均值，用于表征系统粒子的扩散行为，具体公式为

MSD=〈|ri(t)-ri(0)|2〉

(1)

式中，ri(t)表示某一特定粒子i在t时刻的位置矢量；ri(0)为与初始时刻相对应的位置矢量；角括号〈〉表示系综平均值.

根据爱因斯坦方程，由MSD的长时间极限计算自扩散系数[24]，计算公式如下：

(2)

式中，D、N分别表示自扩散系数和粒子总数.

1.2.2 径向分布函数

径向分布函数(radial distribution function, RDF)是一种揭示体系中分子间相互作用等结构特征的重要方法.考虑到分子在空间中随机均匀分布，径向分布函数表示在参考分子确定后，在一定范围内找到另一个分子的可能性，如图2所示.图中，r为所选定的某一范围的半径，dr表示区间.

通过在区间dr内对空间进行离散化，可以获得距离给定分子r和r+dr区间内的分子数，即

(3)

(4)

(5)

式中，n(r)、V、g(r)分别表示dr空间范围内的分子数量、体积和径向分布函数；Nα、ρα、cα分别表示α类分子的总数量、密度和浓度.

2 结果与分析

2.1 分子排布

为了保证模型中的分子排布合理，在进行初步的几何优化后，正则系综(NVT)下，在263～333 K的温度范围内进行1 ns的退火模拟，以获得稳定初始构型，然后进行动力学计算.结果显示，在263、273、283 K等温度条件时，石墨层表面的正十八烷分子排列规则，呈现出明显的分层；并且随着温度升高，距离石墨层表面较远的正十八烷分子的排布逐渐无序；但即使在温度高于烷烃的相变温度(301 K)情况下，如313、323和333 K时，石墨层表面的正十八烷分子依旧排列整齐，如图3所示.

根据动力学计算结果，可以获得模型在各个温度条件下烷烃分子的浓度分布曲线，该曲线表示分子在模型中一定厚度(slab)区间内的密度与其在体系中密度的比值，可以从侧面描述体系中烷烃分子分布情况.如图4所示，在253 K时，正十八烷浓度分布表现出明显的分层特征；同时，在靠近石墨层表面区域的烷烃分布浓度明显要大.随着温度升高，分层现象减弱，正十八烷分子在远离石墨层表面区域出现的几率降低，即说明石墨层对烷烃分子表现出了较强的吸附作用.

(a) 263 K

(e) 303 K

图4 不同温度下正十八烷分子的浓度分布曲线

2.2 势能分量

图5和图6分别表示纯正十八烷体系和石墨层/正十八烷复合体系中的势能分量，即静电能、总势能、总价能和范德华能.其中，静电能和范德华能均属于非键相互作用能，总价能主要描述分子内的相互作用能.如图5(a)所示，随着模拟中温度的升高，静电能明显增加；如图5(b)所示，总价能随着温度的升高而线性增加，这是由于在较高温度下原子更剧烈的振动，并且相变不会明显影响分子内的相互作用；如图5(c)所示，范德华能在总体上也表现出随温度升高而增加的趋势；在图5(d)中可以观察到总势能表现出与静电能同样的现象.这表明相变温度303 K附近总势能的突然变化主要受远距离相互作用的影响，但与静电能和范德华能相比，总势能的增长率变化不明显.

(a) 静电能

(b) 总价能

(c) 范德华能

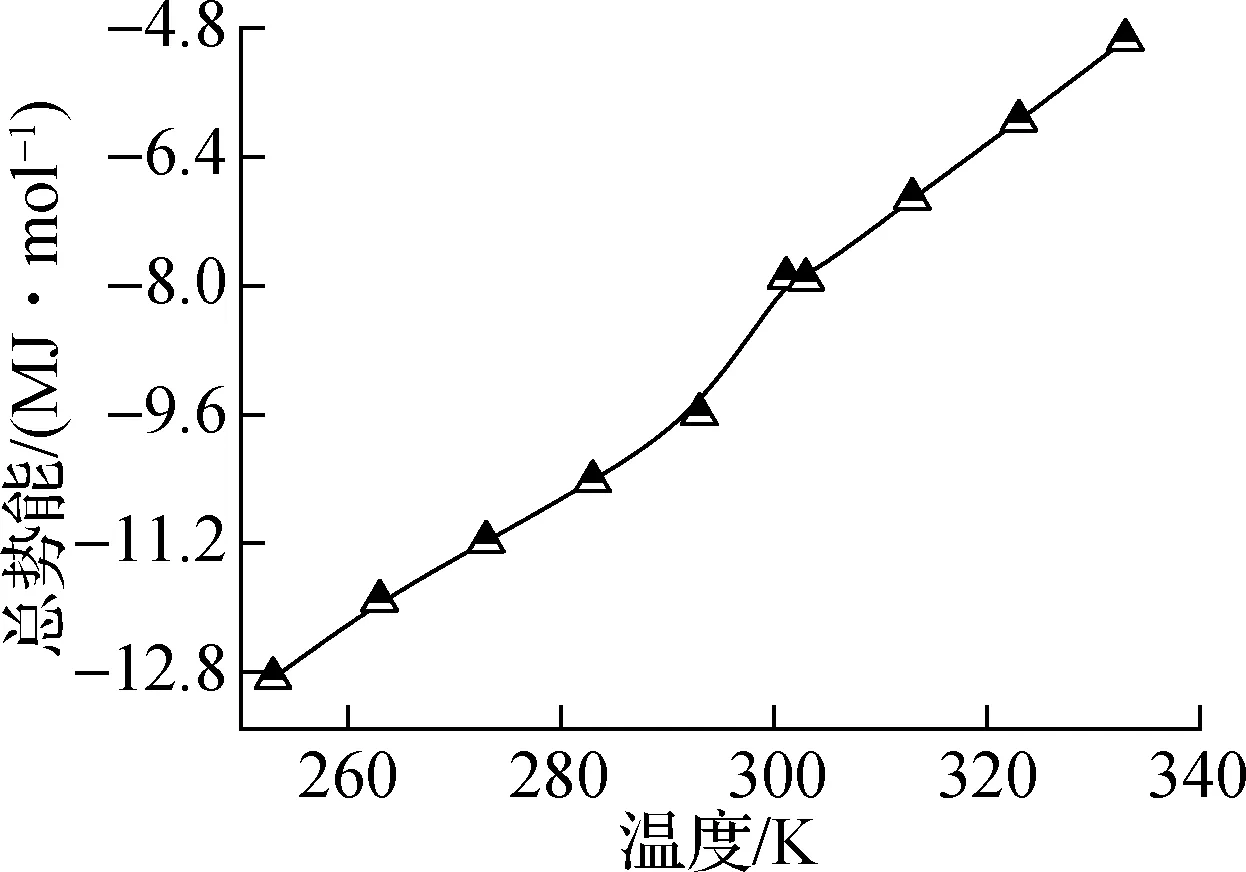
(d) 总势能

由图6可知，体系中添加石墨层之后，石墨层/正十八烷复合体系的势能分量增加速率有突然变化的现象，如图6(a)和(c)所示.但与纯正十八烷体系相比，相变过程中的明显差异表明石墨层对烷烃的微观行为具有影响.石墨层/正十八烷复合体系的相变温度比纯正十八烷体系高约10 K，这可能是由于石墨层对烷烃分子的吸收促进了烷烃分子的结晶.此外，石墨层/正十八烷复合体系的势能分量的增大幅度要弱于纯正十八烷体系，尤其是对于范德华能而言，这说明相变过程中石墨层/正十八烷复合体系中正十八烷分子的构象变化不如纯正十八烷体系中那么明显，即纯正十八烷体系中的扩散强度更大.

(a) 静电能

(b) 总价能

(c) 范德华能

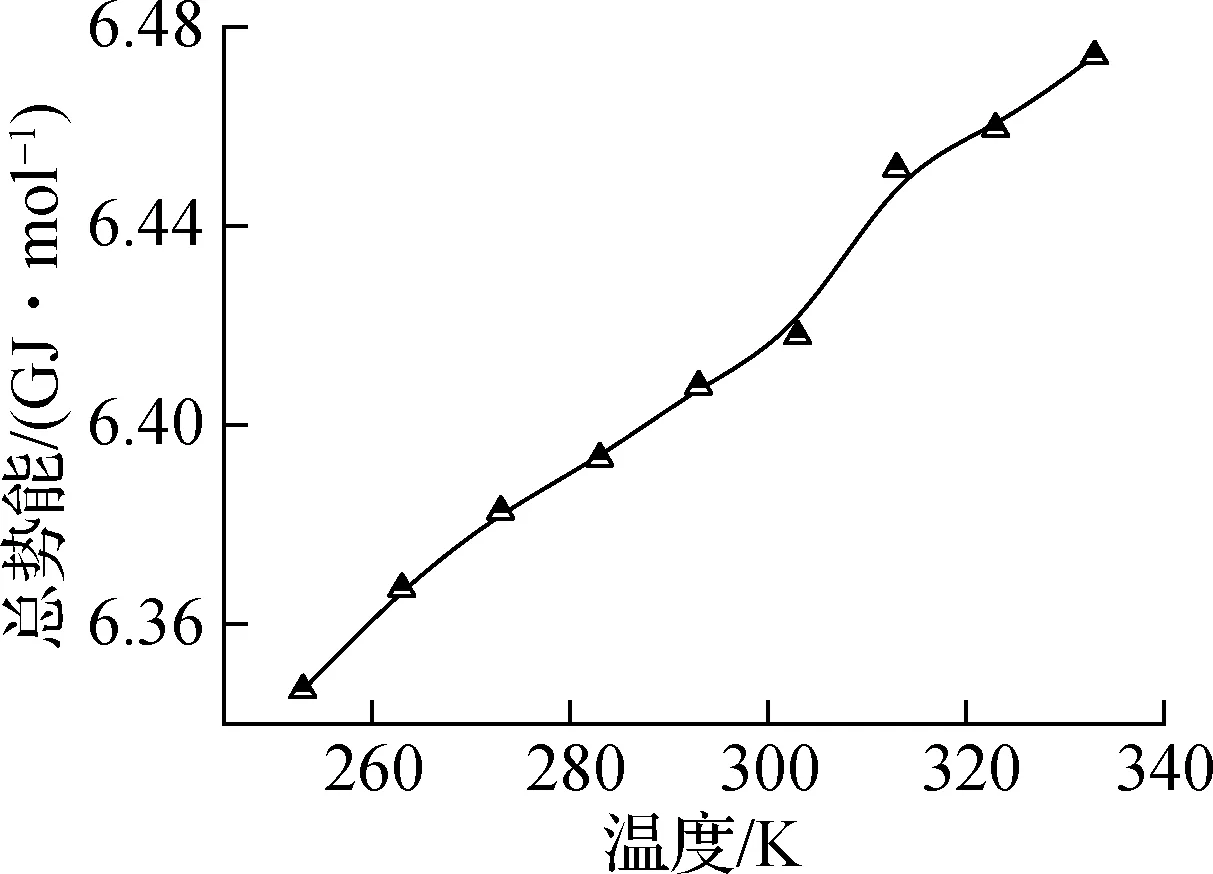
(d) 总势能

2.3 自扩散系数

为了更好地了解石墨层对正十八烷分子排布的影响，本文研究了“三明治”复合相变材料模型中正十八烷分子的扩散性质.根据上述分析中石墨层对正十八烷的吸附作用，分别将模型中的烷烃划分为靠近石墨层的靠近端和远离石墨层表面的远离端2个区域，如图7所示.

图7 模型中不同区域的烷烃(单位：nm)

进一步分别对靠近端、远离端以及全部烷烃分子进行扩散性质研究.均方位移是利用分子轨迹的位移平均值来表征系统粒子的扩散行为，通过计算获得正十八烷分子均方位移的线性部分斜率来表示体系中各部分的自扩散系数.图8为靠近端、远离端以及全部烷烃分子3个不同区域内正十八烷分子的均方位移曲线.由图可知，正十八烷分子的均方位移与时间近似呈线性关系，且随着温度的升高，各曲线的斜率也逐渐增大.

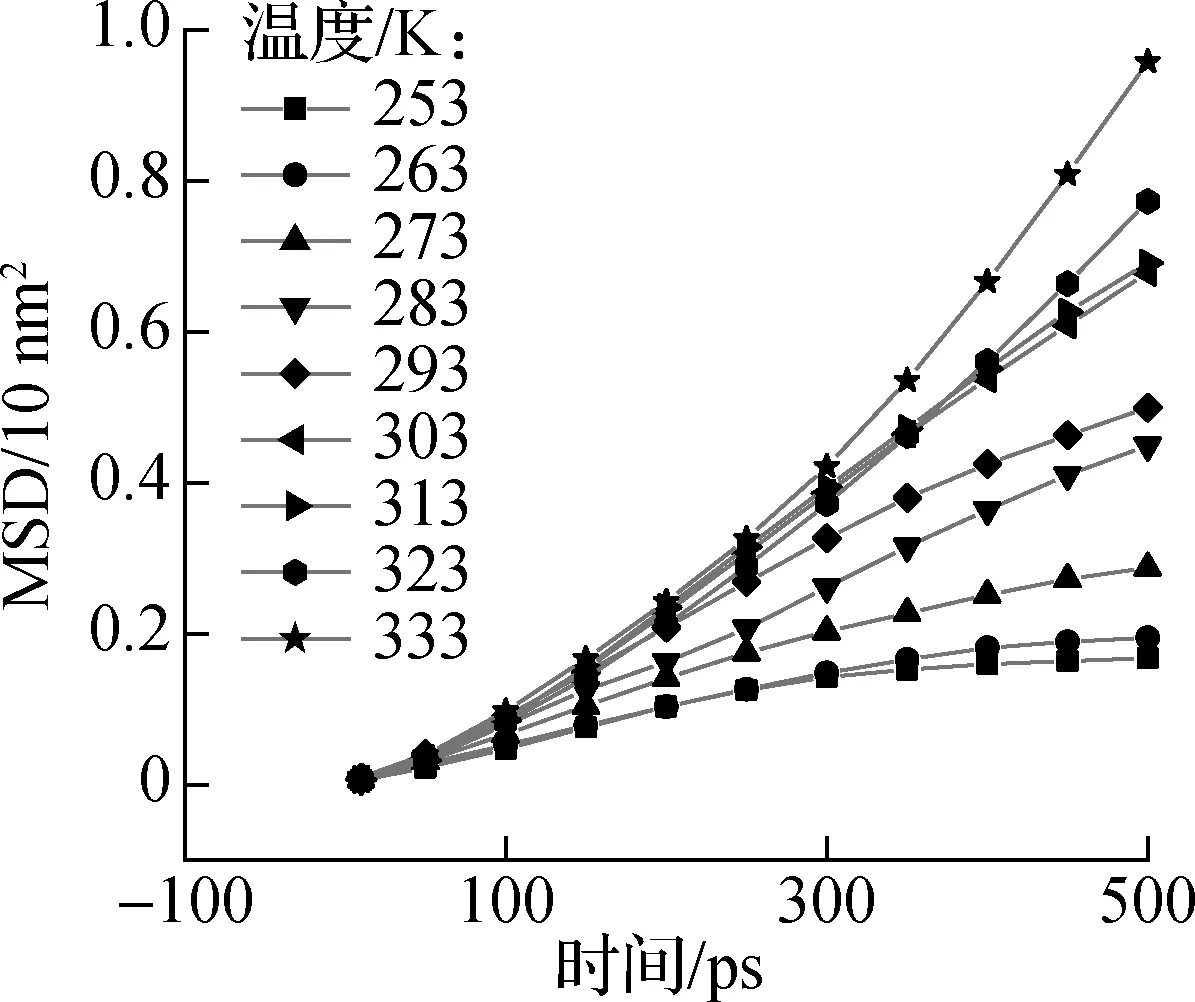
(a) 靠近端烷烃分子

(b) 全部烷烃分子

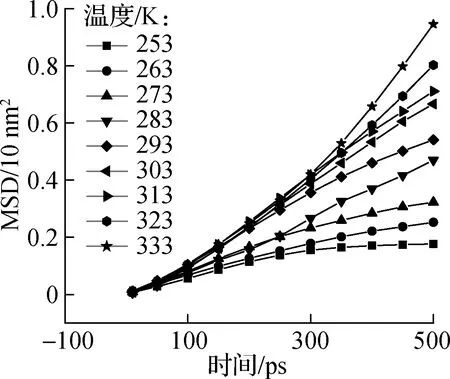
(c) 远离端烷烃分子

根据以上均方位移曲线的斜率获得烷烃分子在体系中的扩散系数.如图9所示，在同一温度下，远离石墨层表面烷烃分子的自扩散系数均高于靠近石墨层表面端烷烃分子；此外，随温度升高，靠近端和远离端的自扩散系数差异变得更加明显.同时对于所有烷烃分子，随温度升高，其自扩散系数呈现增大的趋势.当温度从253 K增加到283 K时，自扩散系数也从0.951 nm2/ns逐渐增加到1.526 nm2/ns；但在293～313 K范围内，自扩散系数从1.655 nm2/ns显著增加到3.356 nm2/ns；由文献[25]可知正十八烷的相变温度在301 K左右，可以推测体系中烷烃分子自扩散系数快速增大的原因是发生了相变，这与2.2节关于势能分量的分析结果一致，也进一步对所建立模型的准确性加以佐证.

图9 不同温度下烷烃分子的自扩散系数

2.4 径向分布函数

径向分布函数表征粒子密度随与参考原子间距离的变化，是描述物质内部微观结构的数学语言，可以从整体角度反映出体系中粒子的聚集特性.由于分子的周期性排列，每层分子对应一个分布峰.在第1邻域出现一个尖峰，代表第1邻域分子之间的结合强度.在较长的距离范围内，液体结构的分布函数会出现一个接近1的扩散峰[26-27].

图10为石墨层/正十八烷复合体系中烷烃分子的径向分布曲线，可以看出在不同温度条件下分别有3个非常明显的峰出现在0.177、0.251和0.307 nm处，即在这3个位置的领域内，正十八烷分子聚集分布.从第1峰的局部放大图来看，随着温度从253 K升高到333 K，该峰的强度从4.347略微降低到3.783，说明复合体系的有序度降低，正十八烷分子在固体状态下的结合强度最大.

图10 不同温度下体系的径向分布曲线

为了获得烷烃相变温度，本文采用了Abraham[28]提出的经验方法，定义参数R为径向分布函数曲线第1谷的谷值gmin与第1峰的峰值gmax的比值，即R=gmin/gmax.如图11所示，可以看到R随着温度的升高而升高；同时，与温度区间253～303 K相比，当温度从313 K增加到333 K时，R增加的趋势明显更大，由此可以推测，在温度为303～313 K的过渡区间内，石墨层/正十八烷复合体系中的正十八烷正在发生相变.

图11 不同温度下体系的R值

3 结论

1) 本文模拟研究了石墨层/正十八烷复合相变材料微观模型中烷烃分子在石墨层表面的吸附行为，结果显示石墨层对烷烃分子表现出较强的吸附作用.在253 K时，正十八烷浓度分布表现出明显分层特征；同时，在靠近石墨层表面区域的烷烃分布浓度明显要大，随温度升高，分层现象减弱.

2) 研究了体系中烷烃分子的扩散性质，结果表明：靠近石墨层表面的烷烃分子的扩散系数明显较小，而且随着温度的升高，自扩散系数显著增加，当温度从253 K增加到283 K时，自扩散系数也从0.951 nm2/ns逐渐增加到1.526 nm2/ns；但在293～313 K范围内，自扩散系数从1.655 nm2/ns显著增加到3.356 nm2/ns；可以推测体系中烷烃分子自扩散系数快速增大的原因是发生了相变.

3) 采用径向分布曲线对烷烃分子在不同温度下的结合强度进行了分析，烷烃发生相变是在温度为293～303 K的过渡区间内.综上，相变材料中添加石墨层可以影响烷烃分子的排布以及扩散，进一步影响了整体材料的导热以及相变性能.