带金属阻尼器的竖向接缝装配式剪力墙受力性能分析
2020-12-22党隆基梁书亭朱筱俊颜欣妍
党隆基 梁书亭 朱筱俊 颜欣妍 张 铭
(1东南大学土木工程学院, 南京 211189)(2东南大学建筑设计研究院有限公司, 南京 210096)
随着可持续发展观念的深入,具有低碳、绿色、环保、节能等特点的装配式混凝土建筑得到了社会的广泛认可.而装配式剪力墙结构作为一种具有良好抗侧性能的结构体系,是我国住宅产业化的主要结构形式.截止到目前,装配式剪力墙结构体系的研究多集中于水平接缝连接形式,并开发了多种连接形式[1-3].现有研究表明,采用“等同现浇”设计理念的剪力墙虽满足刚度和承载力的需求,但剪力墙在地震作用下容易引起应力集聚,发生剪切破坏.
为改善剪力墙结构耗能不足和延性较差的特点,武藤清[4]采用竖向接缝来提高低矮剪力墙的变形能力.近年来,赵伟等[5]和贾斌等[6]进行了钢框架内填预制带竖缝钢筋混凝土剪力墙的抗震性能试验,试件表现出良好的变性能力,但该类剪力墙主要依靠墙体自身的塑性变形来消耗地震能量.随着主动积极抗震技术的推广,在结构或构件的关键部位布置附加耗能装置已被证明是一种合理有效的抗震路径[7].目前,用于装配式剪力墙竖向接缝连接的金属耗能器主要包括椭圆形阻尼器[8]、梳形板[9]、U形板[10]和O形阻尼器[11].这些阻尼器属于面外弯曲耗能,滞回性能稳定但刚度较小.
通常情况下,截面为X形的金属阻尼器(XMD)可实现钢材沿截面全长屈服[12],且具有较高的初始刚度和耗能能力.鉴于此,本文将XMD应用于装配式剪力墙竖向接缝中,致力于改善装配式剪力墙的抗震性能.基于XMD滞回性能试验和带XMD的竖向接缝装配式剪力墙低周反复荷载数值分析,考察了XMD与预制墙板的协同工作机理,以期为竖缝耗能接缝装配式剪力墙的研究提供参考和依据.
1 试验
1.1 试件设计
由文献[13]可知,在面内剪切变形作用下,阻尼器的弹性刚度和屈服剪力与XMD削弱段的宽度和厚度成正比,与XMD削弱段长度成反比.为此,在XMD长度和厚度一定的情况下,本文以削弱段宽度为研究对象,共设计制作了3个试件(见图1).试件XMD20、XMD30、XMD40的削弱段宽度分别为20、30、40 mm,主要设计参数见表1.试件所用钢材厚度均为6 mm,通过材性试验测定钢材的屈服强度为316.11 MPa,抗拉强度为440.53 MPa,断后伸长率为28%.
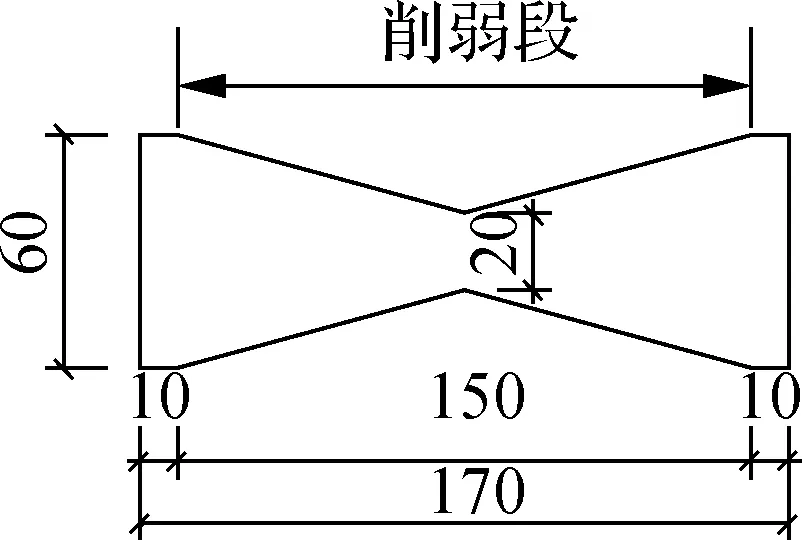
(a) 试件XMD20
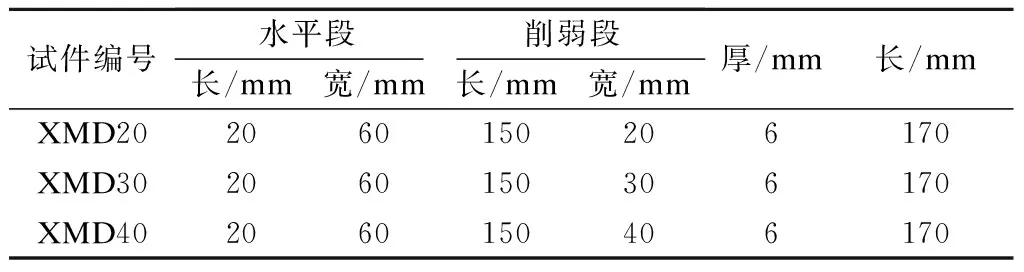
表1 试件的主要设计参数
1.2 加载装置
XMD的测试工作在江苏省交通科学研究院股份有限公司完成,其加载装置示意见图2.试件加载采用量程为50 T的MTS疲劳机,由于MTS疲劳机的几何构造难以实现单个XMD受力性能的测试,因此需通过双T形钢梁来实现2个XMD试件的同时测试,从而获得单个XMD的滞回性能.

图2 试验加载装置
如图2所示,金属阻尼器两端分别焊接于厚度为14 mm的连接板,每个连接板上均有6个直径为12 mm的螺栓孔,其中XMD外侧连接板与双T形钢梁通过螺栓连接,XMD内侧连接板与加载头通过螺栓连接.MTS疲劳机的下夹具用于固定双T形钢梁,上夹具则通过连接加载头施加竖向循环往复荷载.为防止试验过程中加载头发生面外变形,连接装置两侧各布置了一个限位装置.为限制阻尼器在循环荷载作用下面外屈曲变形,2块钢板通过螺栓连接固定于金属阻尼器外侧.
2 试验结果
2.1 滞回性能
试件采取位移控制的加载模式,每级幅值为屈服位移的倍数,其屈服位移根据数值分析确定.由图3所示,试件在整个加载过程中表现出良好的滞回性能.当位移小于0.6 mm时,试件基本处于弹性状态;当位移达到0.6~1.2 mm时,试件进入屈服状态,刚度下降,滞回环面积增大;当位移大于1.2 mm时,试件滞回环形状趋于稳定,呈现饱满的梭形.随着位移的持续增加,XMD与连接板焊缝撕裂,试验结束.试件XMD20、XMD30、XMD40的破坏位移分别为14.4、14.4、10.2 mm.
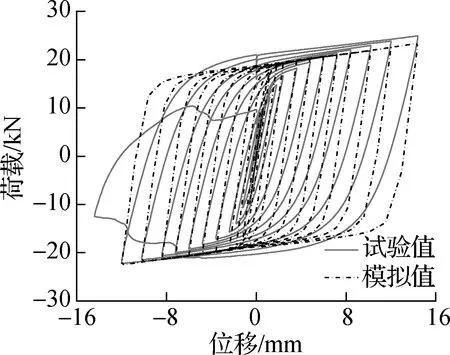
(a) 试件XMD20
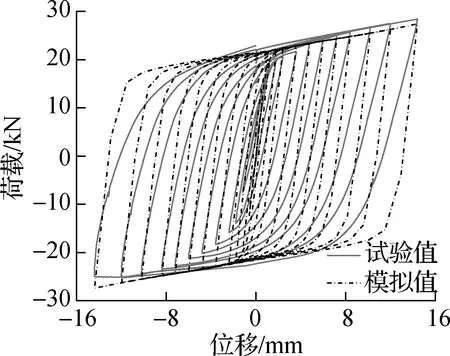
(b) 试件XMD30
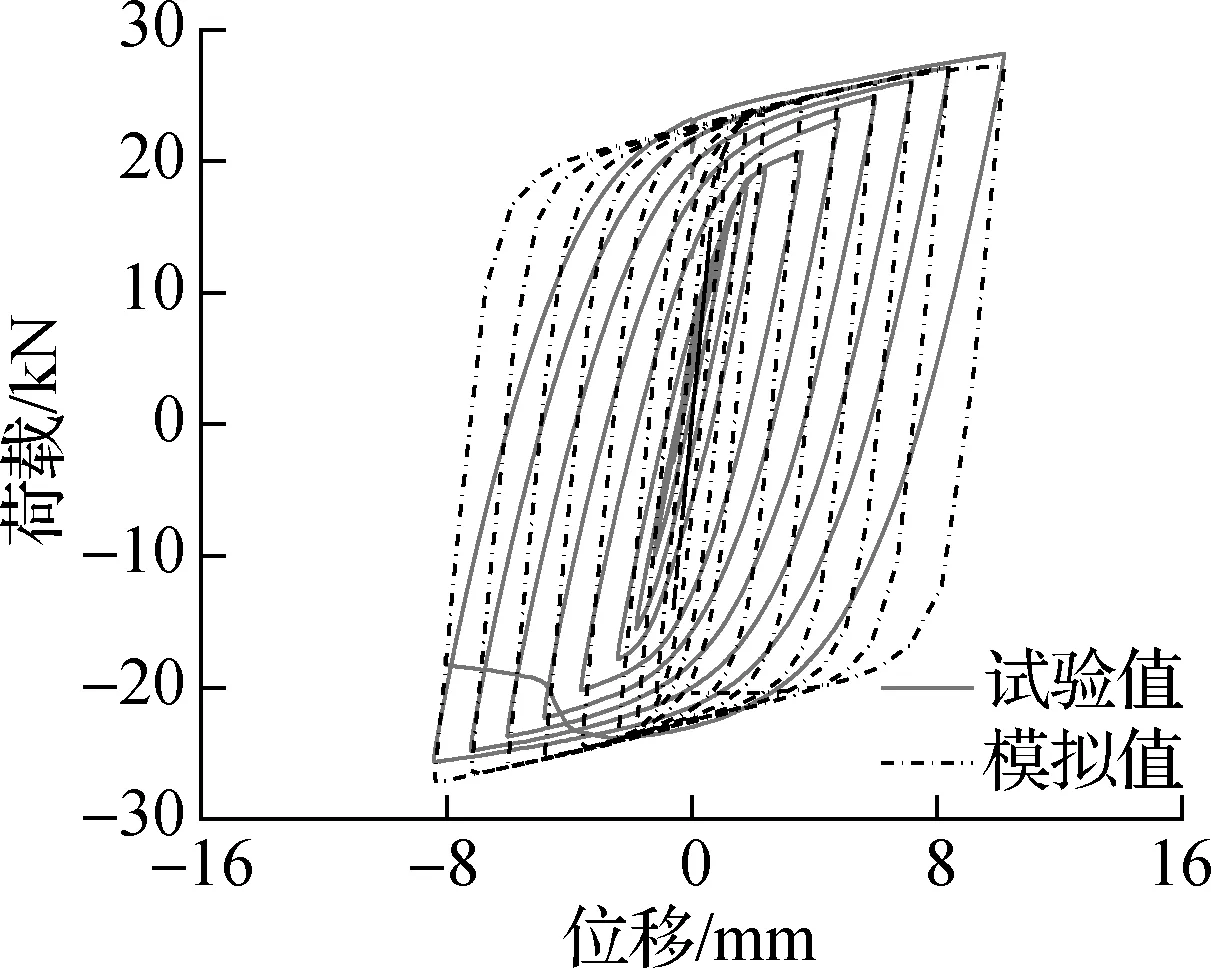
(c) 试件XMD40
2.2 承载力和耗能能力
由图4所示,试件的承载力随着位移的增加而缓慢提高,表现出良好的塑性变形能力.随着削弱段宽度的增大,试件承载力的提高幅度逐渐下降;当位移为8.4 mm时,试件XMD30和XMD40的承载力分别比试件XMD20提高约15.12%和23.78%.
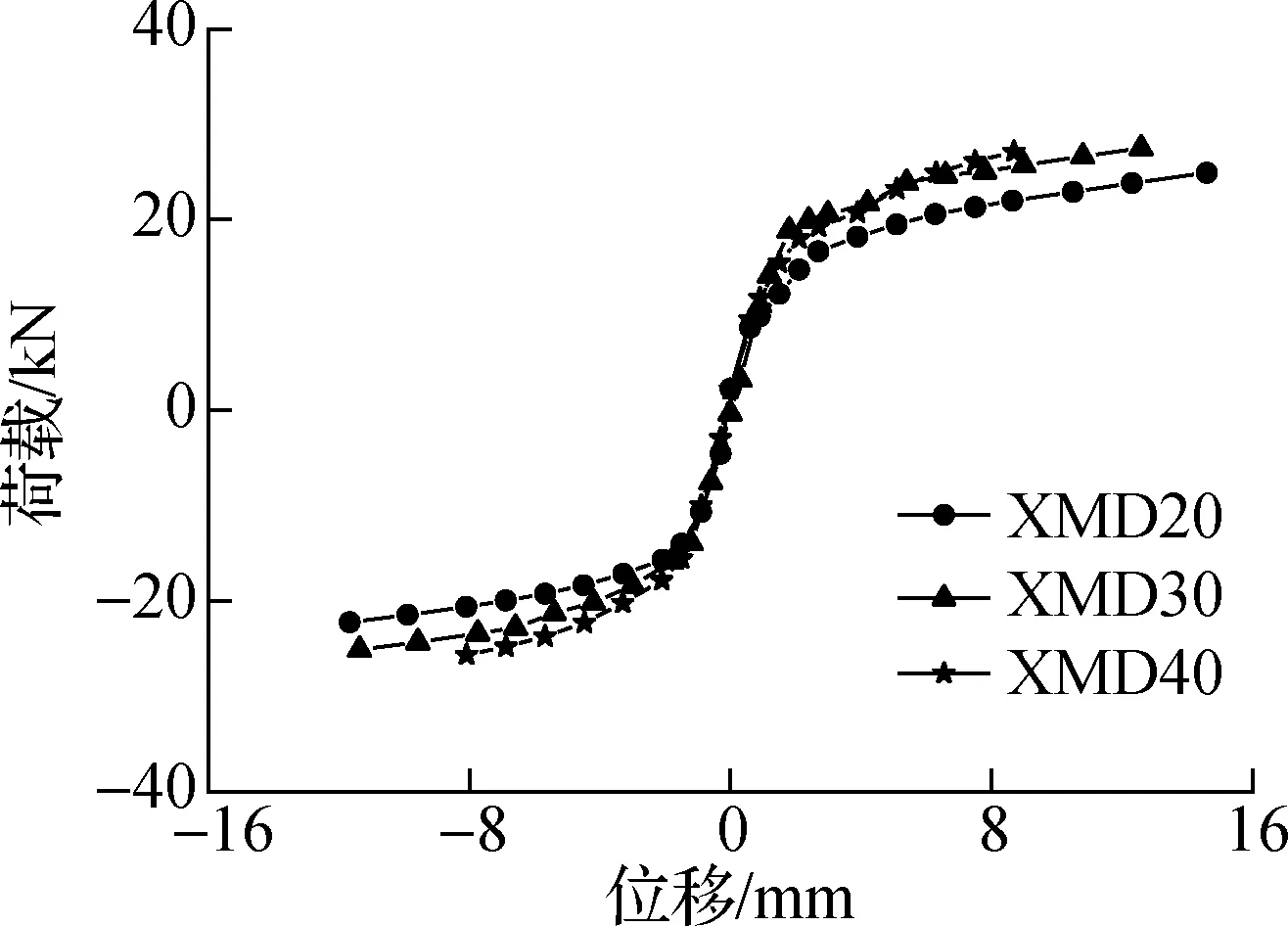
图4 试件的骨架曲线
耗能值和等效黏滞阻尼系数常被用来评价结构或构件在地震作用下耗散和吸收地震能量的能力.图5给出了循环荷载作用下试件单圈滞回环耗能值Ed和等效黏滞阻尼系数ξeq随位移的变化关系.由图可知,在同等位移作用下,试件XMD40的Ed最大,但其ξeq最小.当位移为8.4 mm时,试件XMD30和XMD20的ξeq分别为0.394 2和0.388 9,分别比试件XMD40提高约3.65%和5.06%.因此,XMD的耗能能力随着削弱段宽度的增加而降低.
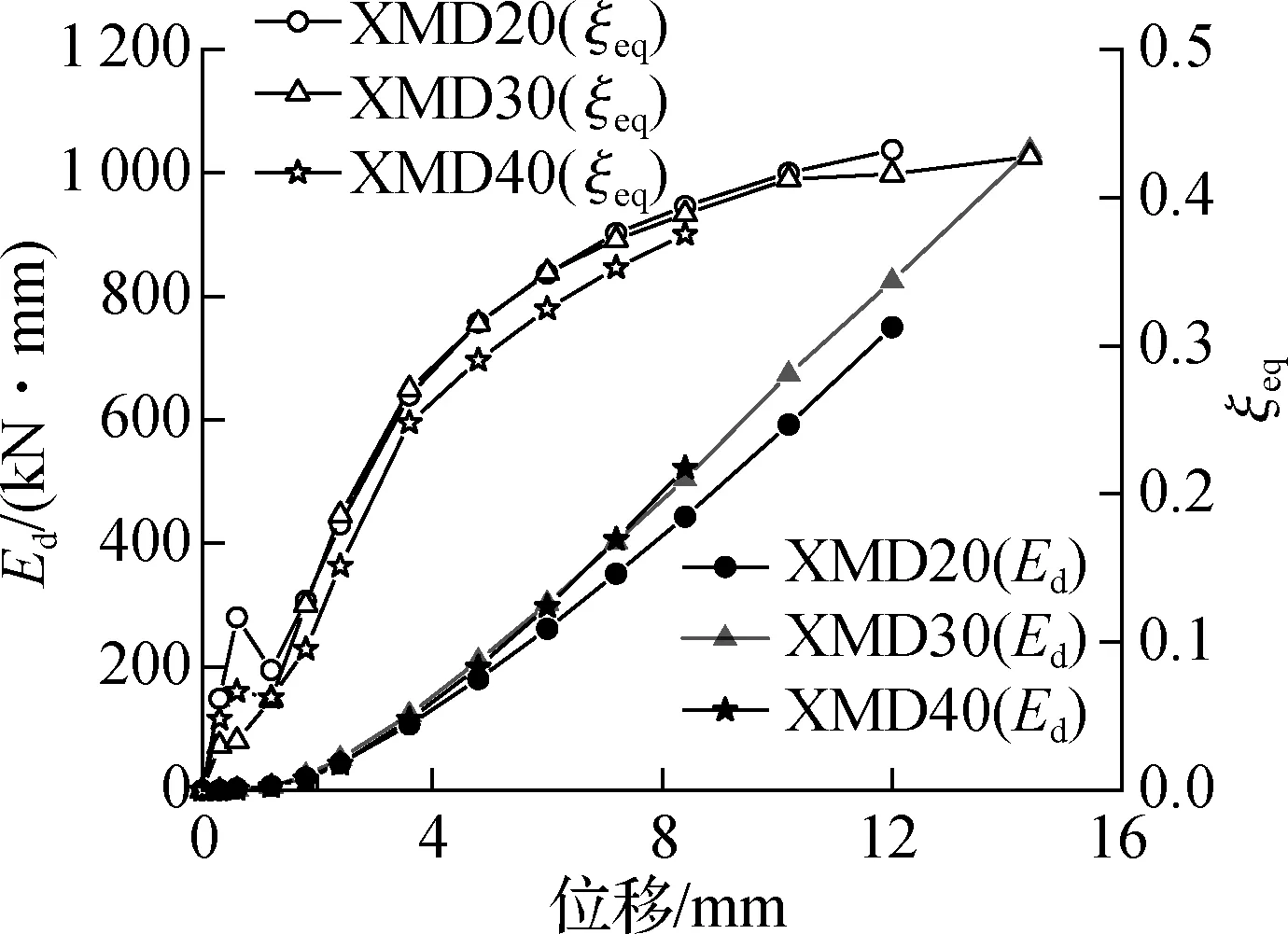
图5 试件的耗能能力
3 竖向耗能接缝装配式剪力墙抗震性能分析
由单个X形金属阻尼器在循环荷载作用下的滞回性能可知,试件XMD20的变形能力优于试件XMD30和XMD40.为此,本文将试件XMD20作为耗能连接件应用于装配式剪力墙竖向接缝中,并基于数值分析的方法研究金属阻尼器数量对装配式剪力墙抗震性能的影响.
3.1 试件设计
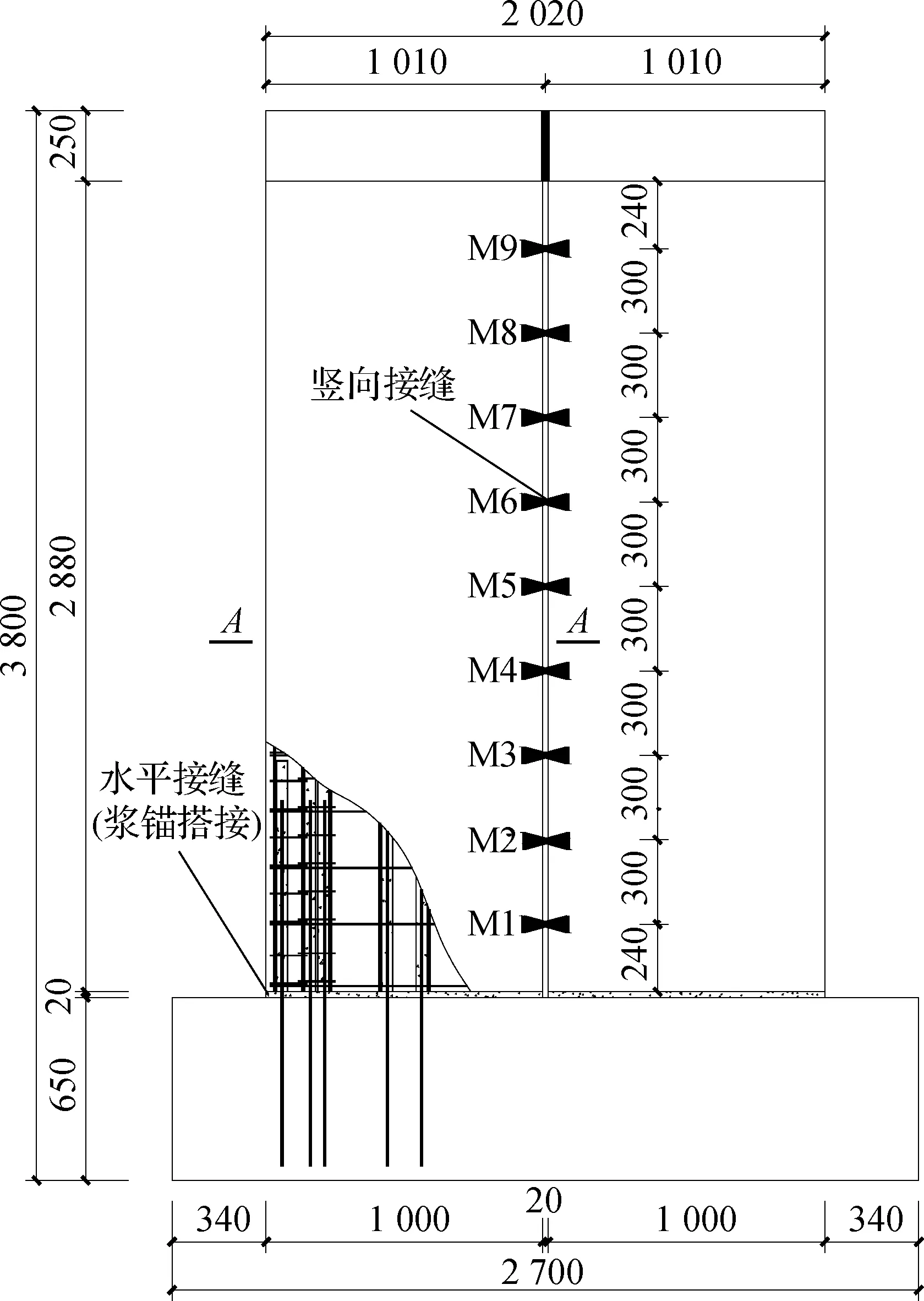
(a) 立面图
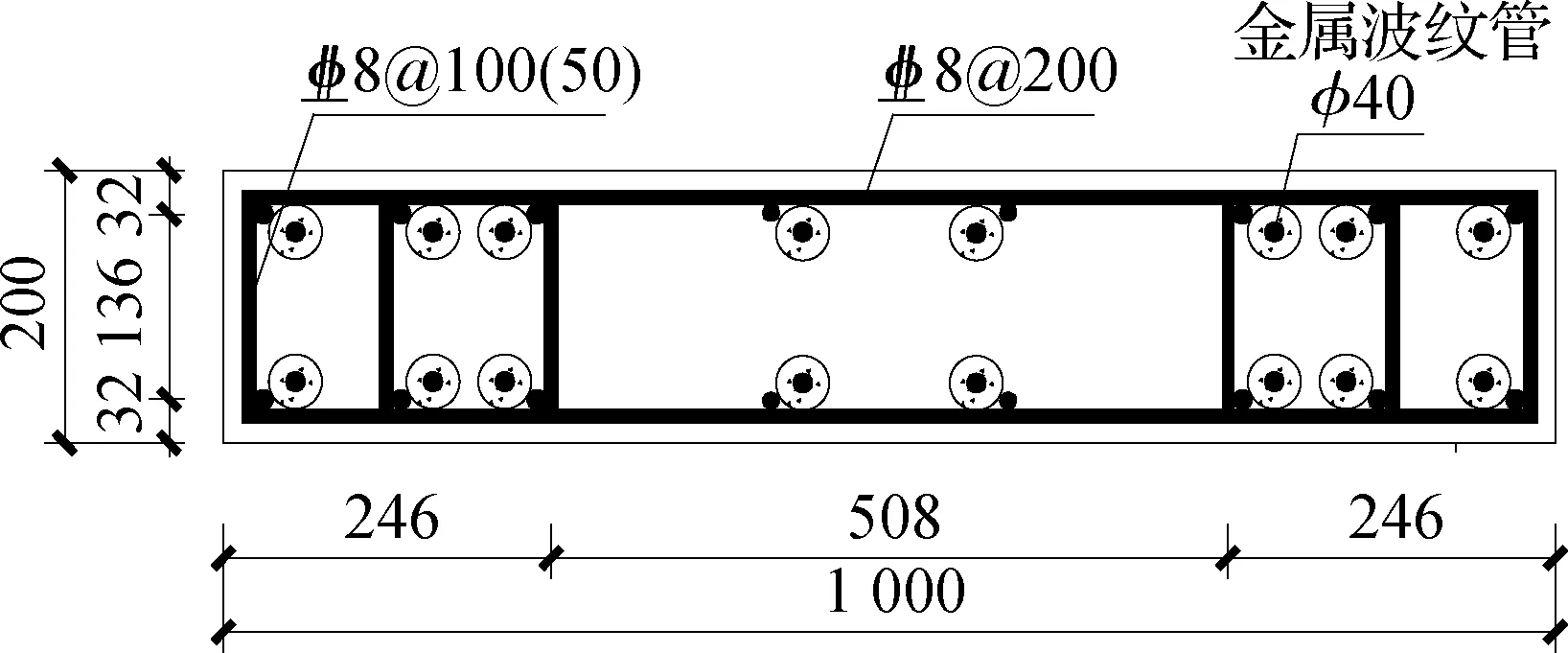
(b) A-A剖面图
3.2 有限元验证
采用有限元软件ABAQUS建立竖向耗能接缝装配式剪力墙的数值分析模型.为验证数值分析模型的准确性,选择文献[16]中的试件RCSW和文献[17]中的试件SW-1作为验证模型,其试件高宽比为1.84和1.65,与设计试件的高宽比(1.5)较为接近.
3.2.1 材料属性
试件钢筋均采用CLOUGH恢复力本构模型,并基于ABAQUS平台开发的子程序实现[18].此外,阻尼器XMD采用二折线本构模型,其屈服强度和塑性应变由钢材材性试验获得,试件XMD20、XMD30、XMD40的数值分析结果与试验结果吻合较好(见图3).
混凝土采用ABAQUS自带的损伤塑性本构(CDP)模型,其应力-应变关系按照《混凝土结构设计规范》(GB 50010—2010)[14]设定.对于CDP模型,经反复计算,最终确定膨胀角为38°,偏移值为0.1,双轴与单轴初始屈服强度比为1.16,黏结系数为0.002,拉压子午面第二应力不变量的比值为2/3,损伤因子为0.90~0.95,受压损伤恢复系数取0.3~0.6.
3.2.2 单元类型与约束条件
混凝土和XMD采用C3D8R单元模拟,钢筋采用T3D2单元模拟,经反复计算,最终确定加载梁和底座网格边长为75 mm,预制墙板网格边长为50 mm,XMD网格边长为5 mm.加载梁与预制墙板之间采用Tie连接,预制墙板与底座之间采用硬接触的方式,以模拟金属波纹管连接.XMD通过Tie连接固定于预制墙板,加载梁之间采用约束方程模拟水平往复荷载的传递.
3.2.3 试验结果与模拟结果的对比
如图7所示,试件RCSW和SW-1的试验结果与模拟结果基本吻合良好,其差异性主要是源于损伤因子和受压损伤恢复系数取值的不同.对于屈服荷载,试件RCSW和SW-1的计算值分别为试验值的0.98和0.84倍;对于峰值荷载,试件RCSW和SW-1的计算值分别为试验值的0.82和0.88倍.以上结果表明,利用本文建模方法可以较好地预测高宽比大于1.5的剪力墙试件.
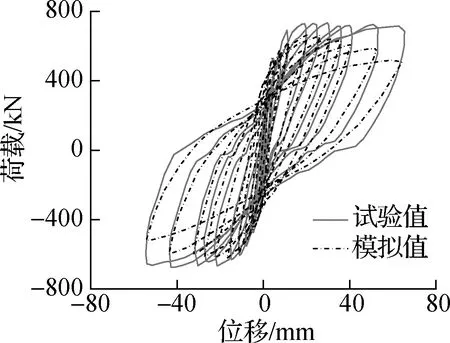
(a) 试件RCSW
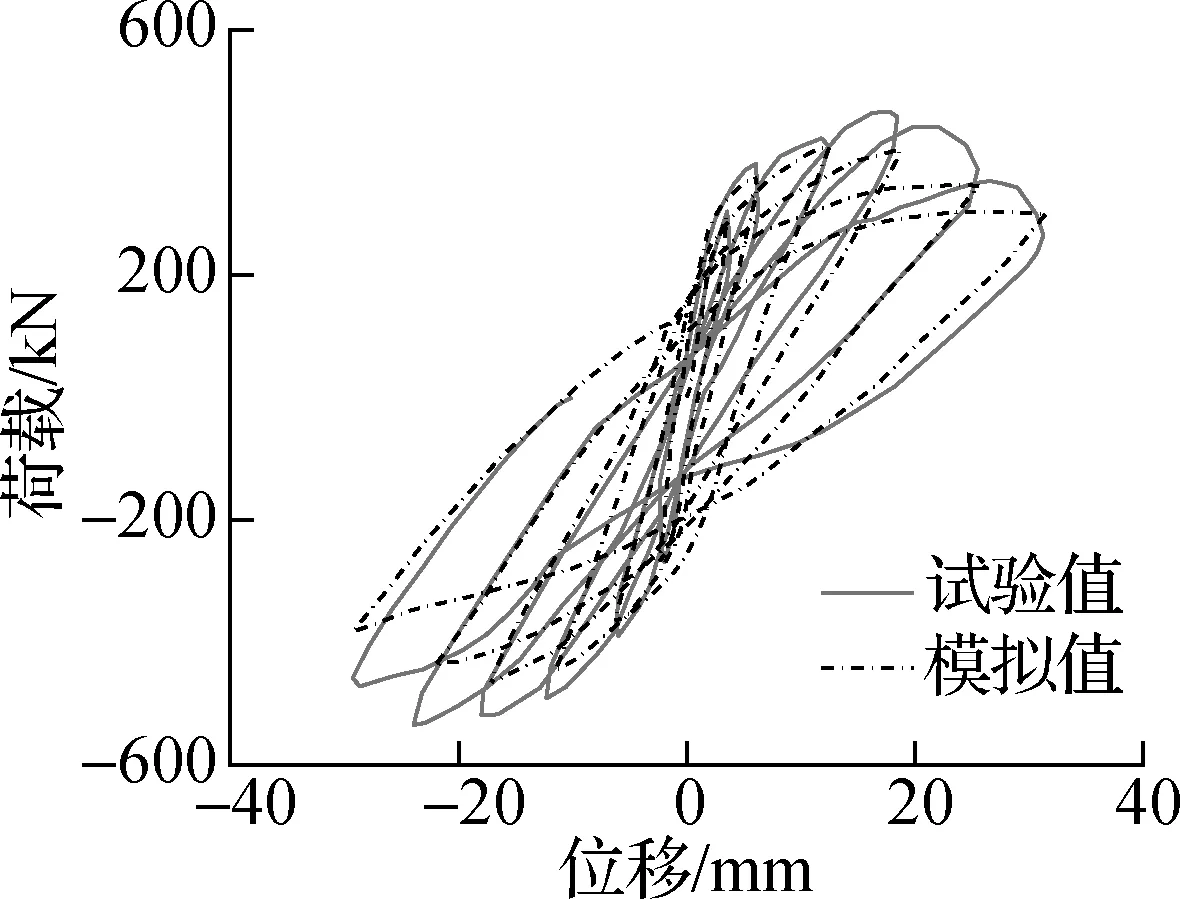
(b) 试件SW-1
4 结果与分析
本文共设计了5个剪力墙模型,考察X形金属阻尼器数量对剪力墙抗震性能的影响.将未布置X形金属阻尼器的试件PSW作为对比试件.试件PSWVEC3、PSWVEC5、PSWVEC7、PSWVEC9中X形金属阻尼器的布置方式见表2.

表2 X形阻尼器布置方式
4.1 破坏形态
图8给出了试件在峰值荷载下混凝土的塑性应变云图.由图可知,试件混凝土塑性变形主要集中于预制墙板底部.试件PSW、PSWVEC3和PSWVEC5混凝土塑性变形区域沿墙板宽度方向斜向分布,表示在金属阻尼器数量小于10的情况下,剪力墙试件以弯剪破坏为主.在低周反复荷载作用下,金属阻尼器与预制墙板协调变形,在一定程度上可增强预制墙板之间的整体性,改善剪力墙的塑性变形能力.当金属阻尼器数量增加至18个时,试件PSWVEC9混凝土塑性变形区域近似呈水平分布,其破坏形态为弯曲破坏.以上结果表明,随着金属阻尼器数量的增加,竖向耗能接缝装配式剪力墙的破坏形态逐渐由弯剪破坏向弯曲破坏转变.
以试件PSWVEC5为例,重点分析金属阻尼器沿墙肢高度方向的应力变化规律.如图9所示,在试件达到破坏荷载时,沿高度方向均匀分布的金属阻尼器均达到屈服强度,表示金属阻尼器应用于装配式剪力墙竖向接缝中具有良好的工作性能.阻尼器M9的应力值最大,阻尼器M1的应力值最小,这是因为剪力墙底部约束强于剪力墙顶部,从而导致剪力墙之间的相对位移随着剪力墙高度的增加而增加.
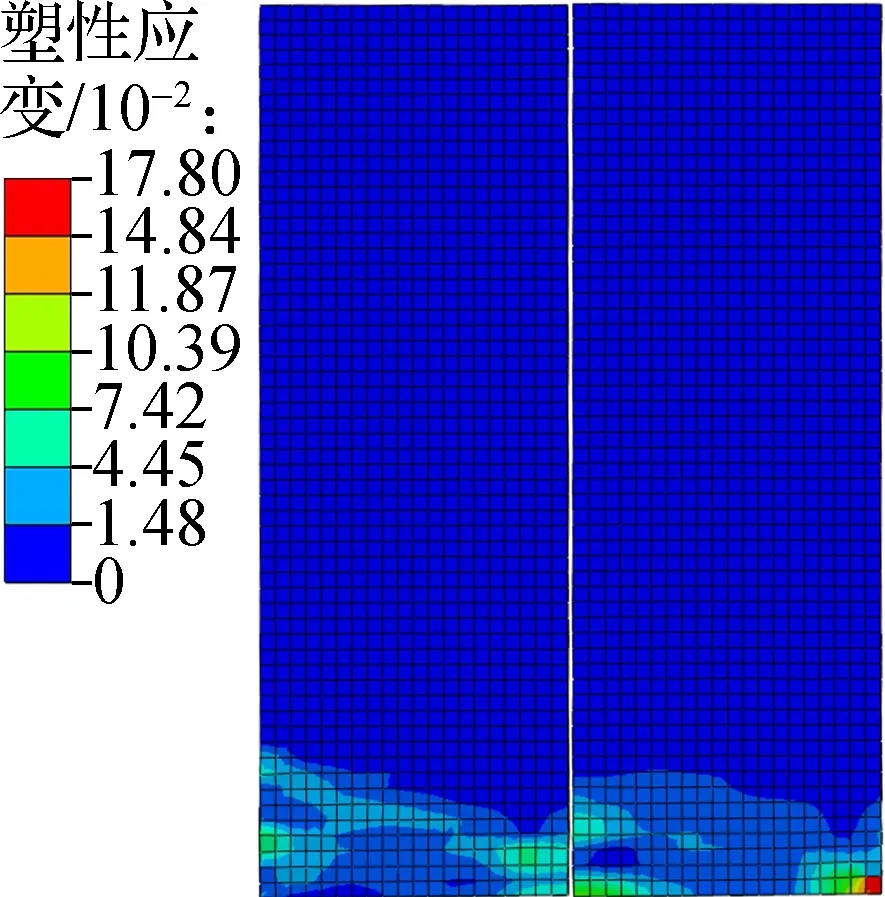
(a) 试件PSW
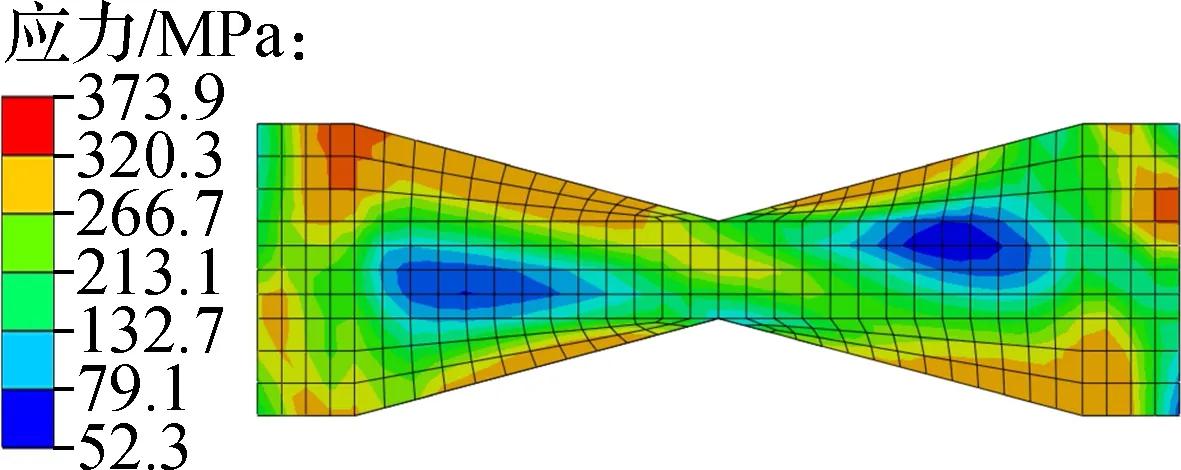
(a) 阻尼器M1
4.2 承载力和延性
图10给出了试件的荷载-位移曲线.由图可知,随着阻尼器布置数量的增加,试件的承载力和刚度均不同程度地提高.与试件PSW相比,试件PSWVEC3、PSWVEC5、PSWVEC7、PSWVEC9的承载力分别提高约19%、24%、29%、32%.
对于带金属阻尼器的装配式剪力墙试件,试件的强度退化曲线随着阻尼器数量的增加而逐渐平缓,表明剪力墙的塑性变形能力随着金属阻尼器数量的增加而提高.经计算,试件PSWVEC3、PSWVEC5、PSWVEC7、PSWVEC9的延性系数分别比试件PSW提高约16%、23%、40%、49%.由此可知,作为竖向接缝连接件,金属阻尼器可提高装配式剪力墙的刚度、延性和耗能能力,但提高程度随着金属阻尼器数量的增加而逐渐减小.
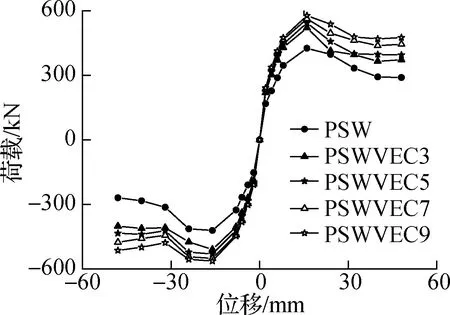
图10 试件的荷载-位移曲线
4.3 相对位移
如图11所示,在低周反复荷载作用下,竖向耗能接缝装配式剪力墙中预制墙板之间产生相对位移,布置于竖向接缝的金属阻尼器在相对位移作用下发生变形.因此,需要对预制墙板之间的相对变形进行分析.
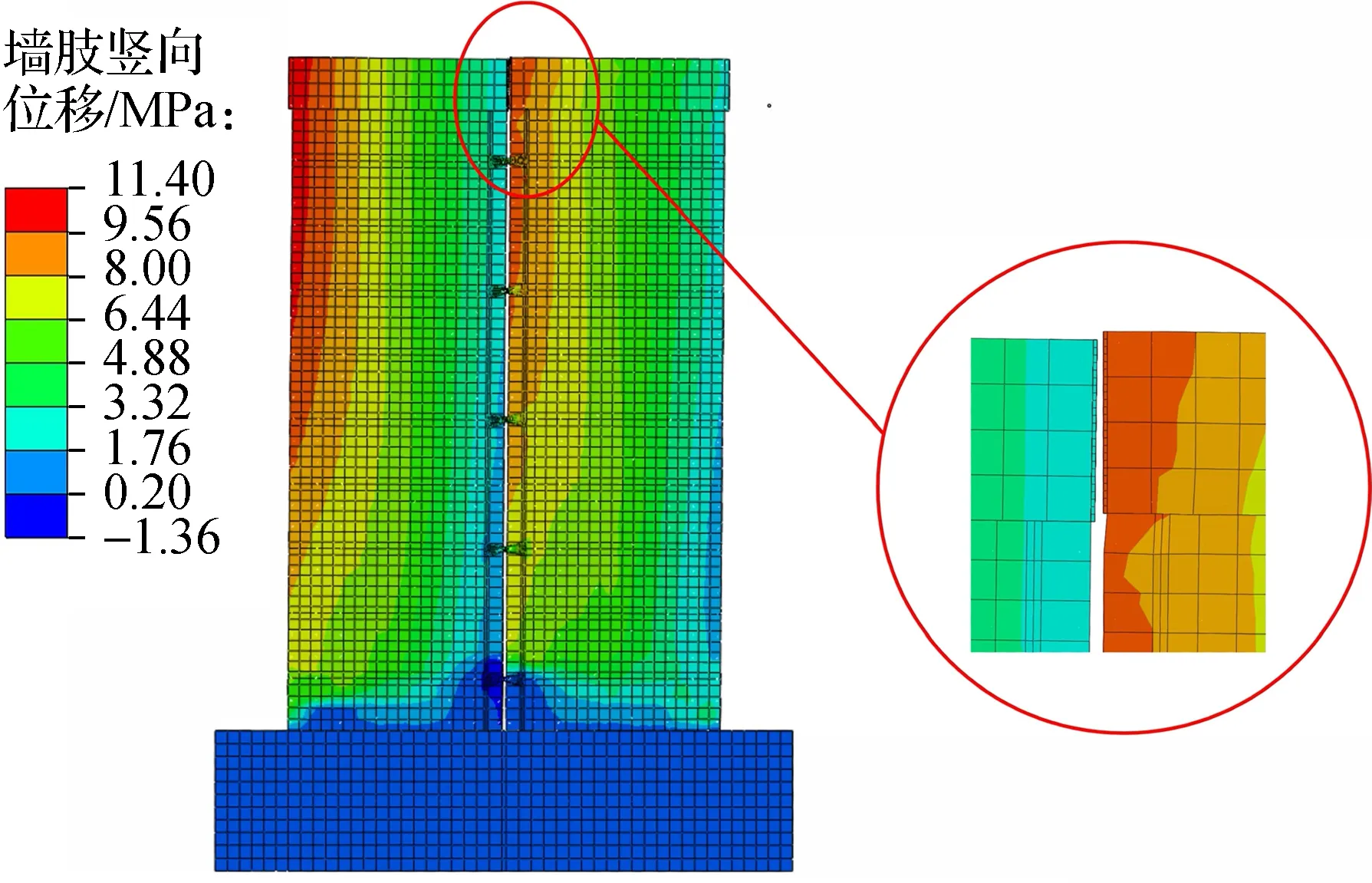
图11 预制墙板相对位移示意图
以剪力墙加载点位移32 mm为例,预制墙板相对位移Δs随剪力墙高度h的变化情况见图12.由图可知,预制墙板相对位移随剪力墙高度的增加而增加.沿墙肢高度方向0~250 mm处,由于预制墙板底部与底座属于湿式连接,剪力墙底部混凝土破坏较为严重,因此预制墙板相对位移出现波动,同时由于底座对预制墙板底部的约束作用导致预制墙板间相对位移较小;随着底座对剪力墙约束效应的弱化,相对位移逐渐增加并趋于稳定.预制墙板相对位移随着金属阻尼器数量的增加而减小,当XMD数量从0增加至18时,预制墙板间的相对位移减少约30.74%,表明金属阻尼器可增强带竖向接缝装配式剪力墙的整体性.
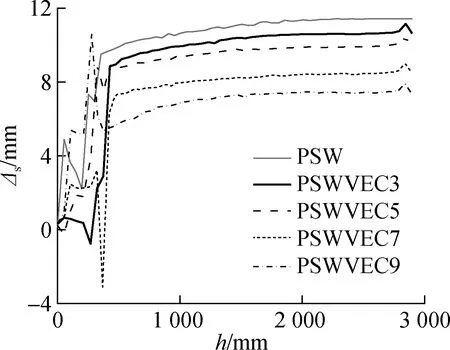
图12 相对位移与剪力墙高度的变化关系
4.4 耗能能力
图13给出了试件耗能值随水平位移的变化关系.图中,Ed表示竖向耗能接缝装配式剪力墙的耗能值.由图可知,试件的耗能值随着阻尼器数量的增加而提高.与试件PSW相比,试件PSWVEC3、PSWVEC5、PSWVEC7和PSWVEC9的耗能值分别提高约17.81%、34.50%、42.39%和52.31%.为充分评估X形金属阻尼器对竖向耗能接缝装配式剪力墙耗能能力的提高程度,对试件XMD20耗能值随位移的变化关系进行线性拟合,其拟合公式为
Ed=-0.067 49+0.075 17Δd
(1)
式中,Δd为试件XMD20加载点的位移.
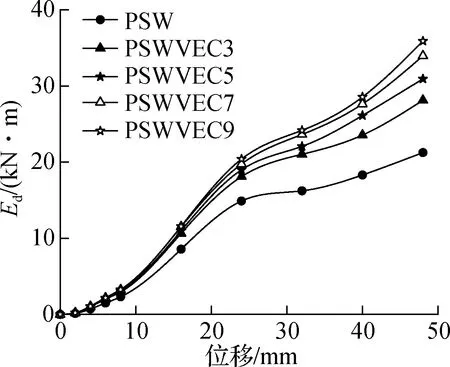
图13 试件耗能值
试件XMD20的试验结果与拟合结果对比见图14.由图可知,当剪切位移小于12 mm时,拟合结果与试验结果吻合良好,XMD20的耗能值与位移近似为线性关系.
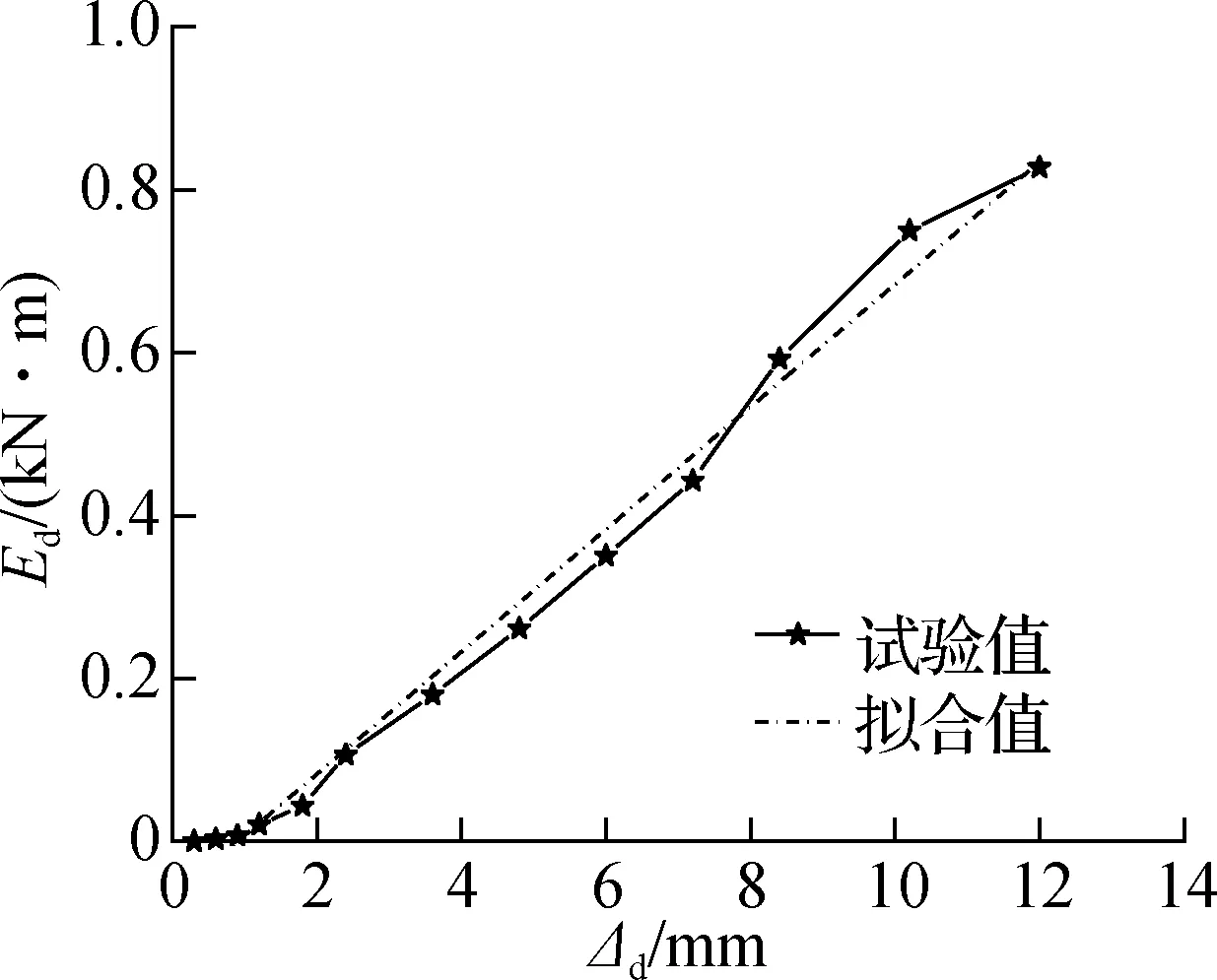
图14 试件XMD20的耗能值
竖向耗能接缝装配式剪力墙的耗能值Ed主要由剪力墙自身耗能值Ed2和金属阻尼器耗能值Ed3组成,并定义Ed4=Ed2+Ed3.Ed可由试件的滞回曲线获得,Ed3可根据式(1)计算得到.图15给出了试件Ed和Ed4随加载等级变化的对比结果.由图可知,在整个加载过程中,竖向耗能接缝装配式剪力墙的耗能值可近似等于剪力墙自身耗能值与金属阻尼器耗能值之和.以试件达到破坏位移为例,试件PSWVEC3、PSWVEC5、PSWVEC7和PSWVEC9的Ed4/Ed分别为0.91、0.99、0.98和1.02.
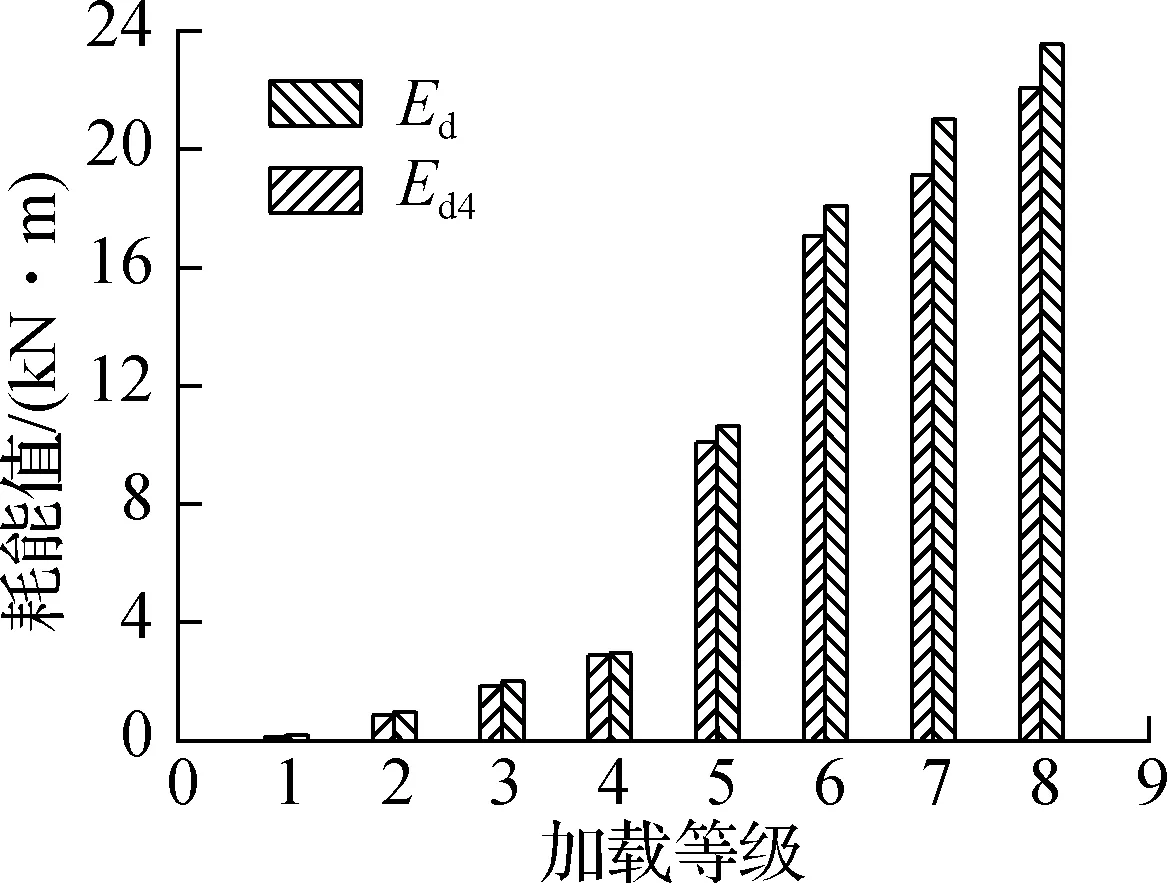
(a) PSWVEC3
5 结论
1) X形金属阻尼器在循环荷载作用下表现出良好的滞回性能.阻尼器的刚度和承载力随着削弱段宽度的增加而提高,但其耗能能力随着削弱段宽度的增加而降低.
2) 在低周反复荷载作用下,X形金属阻尼器与预制墙板之间表现出良好的协同工作性能.随着金属阻尼器数量的增加,试件的破坏形态逐渐由弯剪破坏向弯曲转变.
3) 竖向耗能接缝装配式剪力墙的刚度、承载力、延性和耗能能力随着金属阻尼器数量的增加而提高,但提高的幅度逐渐降低.竖向耗能接缝装配式剪力墙的耗能值可近似等于剪力墙自身的耗能值与阻尼器耗能值之和.
4) 预制墙板相对位移沿墙板高度方向逐渐增加.预制墙板相对位移随着金属阻尼器数量的增加而减小,当XMD数量从0增加至18时,预制墙板间的相对位移减少约30.74%.
