连续型经狭窄腔检测机器人结构设计及运动学分析

周正东 贾峻山 魏士松 刘传乐 章栩苓 毛 玲

(南京航空航天大学机械结构力学及控制国家重点实验室, 南京 210016)

将仿生设计学与机器人技术相结合而产生的仿生机器人，使得机器人技术领域的研究得到了极大的发展.人们在对章鱼触角、象鼻、蛇等生物的仿生学研究中诞生了连续型机器人的设计灵感[1].连续型机器人不具有传统意义上的关节形式和刚性的连杆，通过弹性变形使机器人产生不同形状的连续弯曲运动，是一种新兴的仿生机器人[2].连续型机器人具有弯曲半径小、柔性高、动作灵活的特点，能够在复杂狭小工作空间内工作，对多障碍物和非结构化环境具有极强的适应能力[3]，其应用前景广阔，特别适用于微创医疗、核设施及航空发动机检修、太空未知环境探索等特殊场合.

近年来，国内外针对连续型机器人进行了研究，并取得了一定的进展.在航空维修领域，Niu等[4]对飞机油箱检查连续机器人结构及运动学进行了研究，并进行了仿真和实验验证；向立清等[5]对航空发动机原位检测的连续型机器人运动学开展了研究；Dong等[6]对发动机叶片检测的连续型机器人进行了理论探讨和样机制作.在微创医疗领域，胡海燕等[7]设计了一款用于结肠疾病检查的医疗机器人，并对其通过性进行了研究；杨正馨[8]研制了单孔腔手术连续型机器，并对所提出的切口式柔性杆进行了运动学和力感知研究；Rosen等[9]研制了头颅微创手术机器人，其末端有内窥镜、手术钳和剪刀等装置，可对患者头颅进行微创手术.Sato等[10]设计了一款拆解式体内装配的3自由度手持式机械装置，通过微创孔进入人体对肝脏进行超声扫描成像；为防止器官形变而影响成像结果，Arata等[11]提出了一款具有弹性保护功能的腹腔镜超声扫描装置.荣健等[12]针对蒸汽发生器出口接管焊缝的检测问题，基于UR10机械臂开展了焊缝无损检测机器人的研究.英国OC Robotics公司对工业用连续型机器人进行了开发，并将其产品成功应用于航空、核工业等领域[13].

在精准微创医疗应用中，医护人员时常需将检测装置通过微创孔进入体内并对病变组织进行全方位检测成像，检测装置需具有多自由度及高通过性；在工业无损检测领域，核设施及狭窄腔体等特殊工况中，人员无法达到需要检测的目标位置，需借助机器人实施作业；由于工作环境非结构化特性，机器人须具有良好的弯曲性及通过性，才能更好地完成经狭窄腔开展多方位大范围的检测任务，然而现有的机器人难以满足上述经狭窄腔进行大范围检测作业的需求.为此，本文设计了一种新颖的连续型机器人，运用几何分析方法对所设计的线驱动连续型机器人进行运动学建模，分析单组关节运动学映射关系，并对其工作空间进行分析；提出了多组关节协同运动时的解耦运动学算法；利用MATLAB分别对单组关节和2组关节进行了运动学仿真，以验证运动学算法的可行性和有效性，为后续机器人系统的研制奠定了理论和技术基础.

1 机器人系统结构的设计与分析

传统的连续型机器人大多都是以单根弹性芯柱状物体作为中心骨架，且轴向没有约束变形的机构，这种结构会对机器人的刚度和精度产生影响.影响连续型机器人刚度的主要原因为：在驱动线受到张力时，对机器人的支撑连接件产生侧向作用力，对连续型机器人的中心骨架产生扭矩，从而使中心骨架发生扭曲变形[14-15]，同时当驱动线受到张力时，中心骨架还会产生一定的轴向压缩.影响连续型机器人精度的主要原因为：机器人发生弯曲变形时没有恒定的曲率[15].

为满足经狭窄腔开展多自由度大范围检测作业的需求，并从结构上提高连续型机器人的刚度和精度，在保证曲率恒定的前提下，防止扭曲变形及轴向压缩变形，本文提出了一种具有万向节和圆柱螺旋弹簧约束的新型连续型机器人.

1.1 机械结构设计

连续型经狭窄腔检测机器人采用圆柱形外形设计，由支撑圆筒、内部传动轴、万向节、圆柱螺旋弹簧、驱动线、驱动线导轮、驱动模块组成，如图1所示.在支撑圆筒之间采用万向节及圆柱螺旋弹簧作为关节支撑，可以保证机器人弯曲后具有一定的刚度和恒定的曲率.

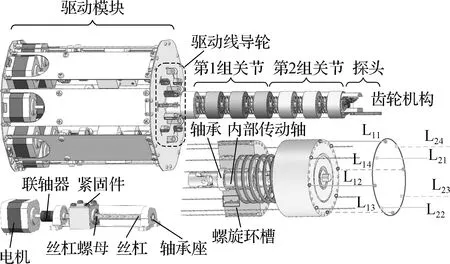
图1 连续型经狭窄腔检测机器人结构图

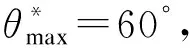
1.2 驱动原理

驱动模块中丝杠装置的直线运动使驱动线受到张力作用，且支撑圆筒间的驱动线线长发生变化，引起万向节的偏转及圆柱螺旋弹簧的弯曲，从而使连续型机器人实现弯曲运动，其驱动原理如图2所示.

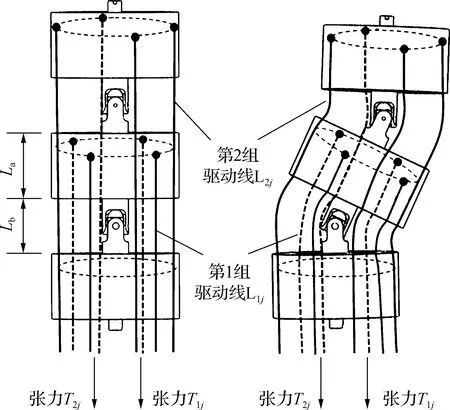
图2 驱动原理图

当第1组驱动线受到一组张力T1j并处于紧绷状态时，第1组关节达到某种弯曲姿态并处于锁定状态，此时的第1组关节可视为第2组关节的“基座”；当第2组驱动线受到一组张力T2j时，第2组关节达到某种弯曲姿态，从而实现整个连续型机器人的整体驱动.当张力T1j、T2j分别驱动第1组、第2组关节向相同的方向弯曲，连续型机器人实现类L形弯曲；当张力T1j、T2j分别驱动第1组、第2组关节向相反的方向弯曲，连续型机器人实现类S形弯曲.

根据狭窄腔的具体结构形状调整连续型机器人的弯曲姿态，使末端探头经狭窄腔后，到达目标位置，并通过主轴电机的旋转将动力传输至末端齿轮机构，实现探头的检测动作，机器人弯曲检测示意图如图3所示.

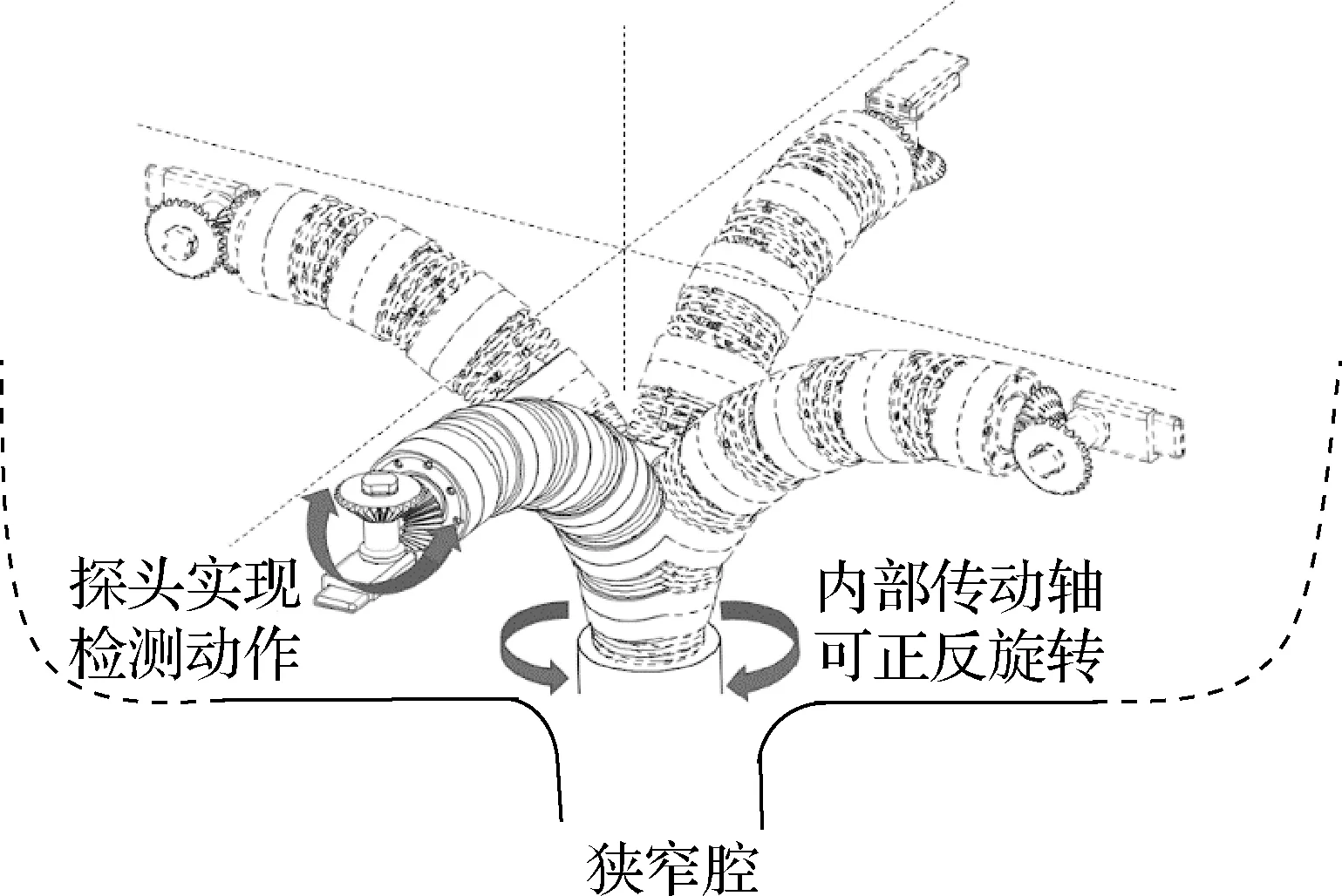
图3 机器人弯曲检测示意图

2 连续型机器人运动分析

线驱动连续型机器人通常不具有刚性关节和连杆，其利用驱动线线长变化引起自身弹性变形使机器人本体发生弯曲而达到某种姿态，故该运动学的分析不仅包括关节空间与操作空间之间映射关系的分析，还应包括驱动空间与关节空间之间映射关系的分析.

所提出的线驱动连续型机器人，各关节的结构相似，自由度相同，下面先以单关节段作为研究对象，建立统一的运动学模型，然后推广至全部关节.

2.1 单组关节运动学分析

为了确定机器人的运动学模型，在连续型机器人的第1组关节起始端支撑圆筒上端面的几何中心、第1组关节及第2组关节最末端支撑圆筒上端面的几何中心分别建立坐标系O0-x0y0z0、O1-x1y1z1、O2-x2y2z2，各坐标系的x轴指向支撑圆筒上被驱动线L11穿过的线孔，y轴指向支撑圆筒上被驱动线L12穿过的线孔，z轴方向由右手螺旋法则确定；连续型机器人的弯曲运动可分解为关节自身的弯曲运动和以坐标系z轴为旋转轴的旋转运动，分别用θ、φ表示弯曲角和旋转角.单组关节运动学模型如图4所示，图中θ为单组关节弯曲角度，θ*为单关节段弯曲角度；绕坐标系O0-x0y0z0的z轴旋转φ后生成坐标系O0-swt，绕坐标系O0-swt的w轴旋转-θ并平移至坐标系O1-x1y1z1原点后生成坐标系O1-s1w1t1；O0OO1平面为单组关节弯曲平面(O为轴s与轴s1的交点)；绕坐标系O0-swt的w轴旋转-θ*并平移至相邻支撑圆筒上端面几何中心后再绕t轴旋转-φ后生成坐标系o1-uve.

(a) 单组关节

2.1.1 关节空间与操作空间映射关系分析

关节空间与操作空间映射关系，即关节变量θ、φ与机器人末端位姿之间的关系.在机器人运动过程中，可由坐标系O0-x0y0z0到o1-uve的齐次变换矩阵T表示单关节段的关节空间至操作空间运动学映射：

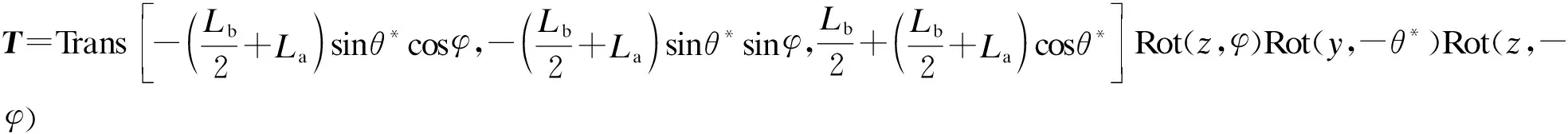
(1)

式中，θ*∈[0,π/3]，φ∈[0,2π]；θ=3θ*.

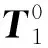
(2)

操作空间至关节空间的运动学映射关系分析是在已知机器人末端位置和姿态的情况下，对机器人弯曲角θ和旋转角φ进行求解.设n、o、a分别为单组关节末端坐标系O1-x1y1z1的x、y、z轴所对应的单位矢量，p为坐标系O1-x1y1z1原点在坐标系O0-x0y0z0中的位置矢量，则机器人末端位姿可由矩阵Tm表示，即

(3)

联立式(2)和(3)，可得单组关节操作空间至关节空间的运动学映射关系：

θ=arccosaz

(4)

(5)

2.1.2 驱动空间与关节空间映射关系分析

驱动空间与关节空间映射关系指机器人弯曲时驱动线线长变化量ΔLij(i=1,2;j=1,2,3,4)与关节变量θ、φ之间的关系.根据图4(b)所示的单关节段运动学模型，先分析单关节段中驱动线线长变化.单关节段的弯曲角θ*和旋转角φ是通过改变2个支撑圆筒之间90°分布的4根驱动线的线长而进行控制的；在单关节段弯曲过程中，万向节和驱动线的弯曲角度相等，但由于驱动线在支撑圆筒端面圆周方向均匀分布，因此尽管弯曲角度相等，但弯曲曲率不同.由图4(b)中的几何关系，可得到驱动线弯曲曲率半径ρij(i=1,2;j=1,2,3,4)等于支撑圆筒上驱动线Lij穿过的线孔与点O之间的距离，则单关节段第1组和第2组驱动线线长变化量为

(6)

(7)

由对单关节段的运动学分析，推广至机器人的单组关节，可得单组关节第1组及第2组驱动线线长变化量分别为

(8)

(9)

2.1.3 单组关节工作空间分析

机器人工作空间是机器人末端所能达到的空间点的集合，由机械结构及关节变量所决定，是一种重要的运动学指标.

由上述关节空间与操作空间映射关系式(1)～(3)，联立式(2)和(3)，可得机器人单组关节末端坐标为

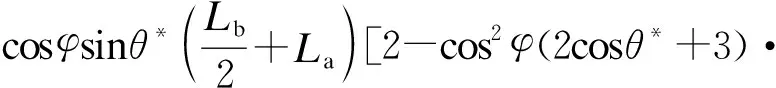
(10)

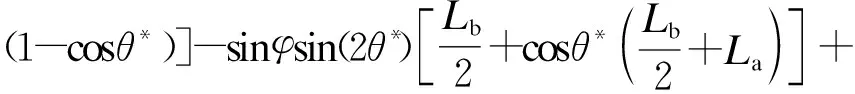
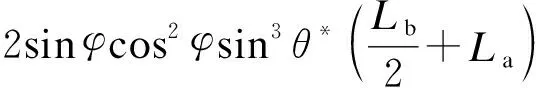
(11)

(12)

其中，La=20 mm，Lb=24 mm，θ*∈[0,π/3]，φ∈[0，2π].

令F(θ*,φ)表示坐标系O0-x0y0z0原点O0到单组关节末端在XOY平面上投影之间的距离，即

(13)

则单组关节的作业半径rw=F(θ*,φ),单组关节最大作业半径R等于函数F(θ*,φ)的最大值.

根据式(10)、(11)和(13)可以求得，当θ*=0.7 rad，即单组关节弯曲角度为θ=2.1 rad时，函数F(θ*,φ)取最大值99.33 mm，即单组关节最大作业半径R为99.33 mm.

机器人单组关节在空间运动时，对于任意给定的旋转角φ，作业半径随弯曲角θ(θ=3θ*，θ∈[0,π])变化的曲线如图5所示.

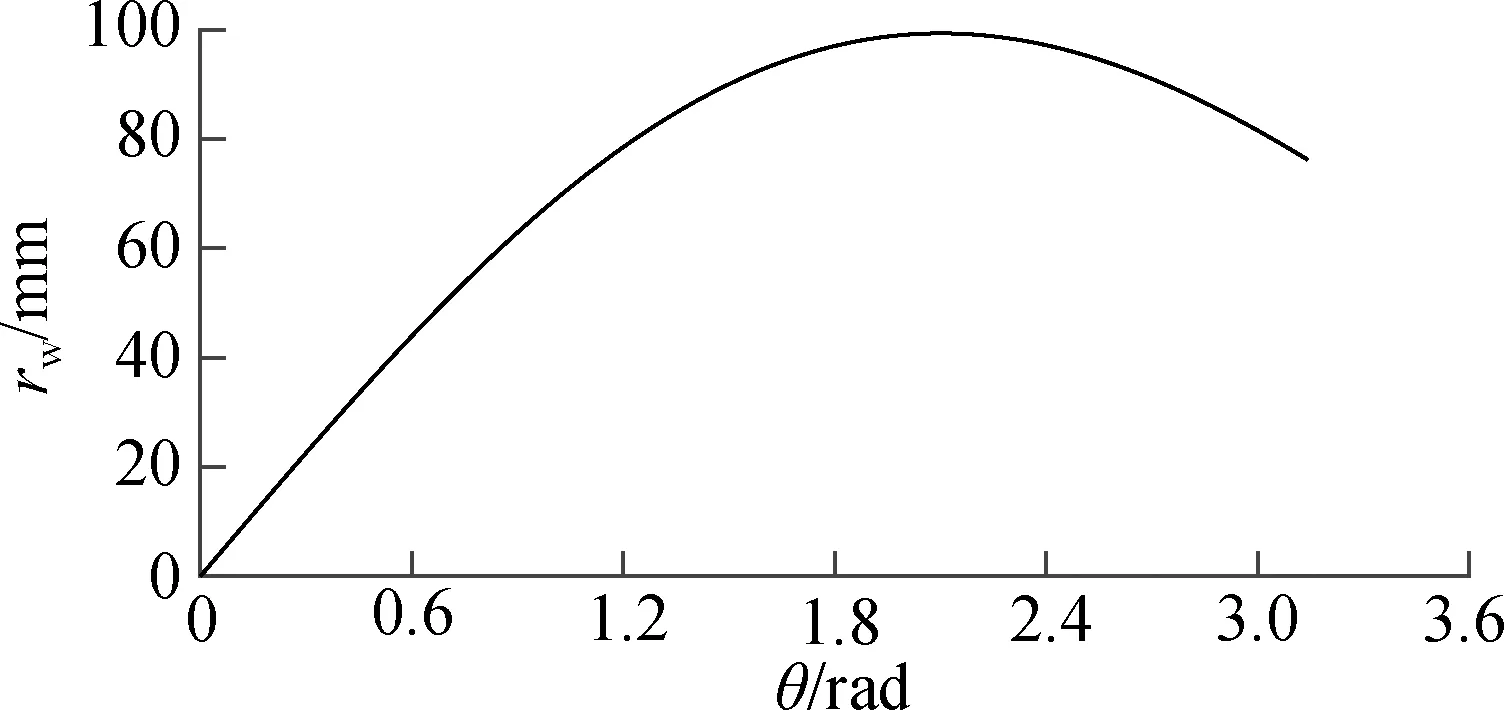
图5 作业半径rw随弯曲角θ变化的曲线图

根据上述分析可确定连续型机器人单组关节末端端点的空间位置分布，利用MATLAB绘制其工作空间点云图，如图6所示.

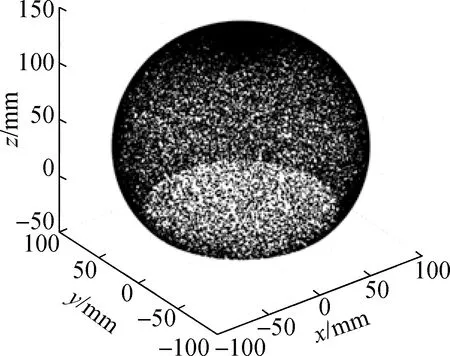
(a) 三维图

从图6可以看出机器人工作空间为一个开口中空球体.所提出的线驱动连续型机器人可经过非通直的狭窄腔后，对内部目标进行多自由度大范围灵活检测作业.与文献[10-11]所提出的刚性结构相比，所提出的结构工作空间大，且机器人本体灵活性高、通过性强.

2.2 多组关节运动学解耦分析

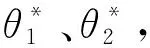
(14)

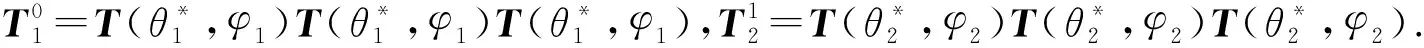
2组关节协同运动时，第2组驱动线线长变化包括2个部分：贯穿在第1组关节中的第2组驱动线线长变化和贯穿在第2组关节中的第2组驱动线线长变化.由单关节段运动学分析，根据式(6)～(9)可得第2组驱动线线长变化量为

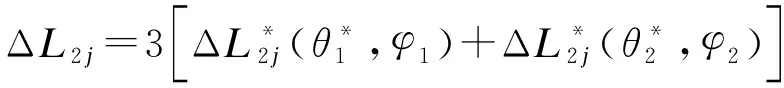
(15)

3 机器人运动学数值仿真

在初始状态下，各组关节驱动线线长不发生变化，第1组关节末端在基坐标系O0-x0y0z0中的坐标为(0,0,132)，机器人末端在基坐标系O0-x0y0z0中的坐标为(0,0,264).根据前述单组关节运动学算法，当第1组关节单独运动时，弯曲角θ∈[0,π]，旋转角φ∈[0,2π]，等间距取50个采样点，第1组关节末端位置变化曲线如图7所示.

图7 第1组关节单独运动时末端位置变化曲线

根据前述多组关节运动学算法，当2组关节协同运动时，可得第2组驱动线线长变化量在[-72.46,45.64] mm范围内变化.设第1组、第2组关节的弯曲角和旋转角分别为θ1∈[0,π/4]和φ1∈[0,2π]、θ2∈[0,π/4]和φ2∈[0,2π]，等间距取50个采样点，机器人实现类L形姿态时末端位置变化曲线如图8(a)所示.设第1组、第2组关节的弯曲角和旋转角分别为θ1∈[0,π]和φ1∈[0,π]、θ2∈[0,π]和φ2∈[π,2π]，等间距取50个采样点，机器人实现类S形姿态时末端位置变化曲线如图8(b)所示.第2组驱动线线长变化曲面图如图9所示.

当2组关节协同运动且完成类L形姿态的过程中，第1组、第2组关节的弯曲角和旋转角分别为θ1∈[0,π/4]和φ1∈[0,2π]、θ2∈[0,π/4]和φ2∈[0,2π]，第1组驱动线线长变化曲面图如图10所示.当仅单组关节完成类L形姿态的过程中，弯曲角θ∈[0,π/2]、旋转角φ∈[0,2π]，第1组驱动线线长变化曲面图如图11所示.

从图10和图11可以看出，与单组关节相比，2组关节协同运动并实现类L形姿态时，驱动线线长变化量小，能更快地达到预定的姿态，且机器人末端可达空间位置更多，能实现多样的姿态，可满足更加复杂的非结构化环境作业需求.

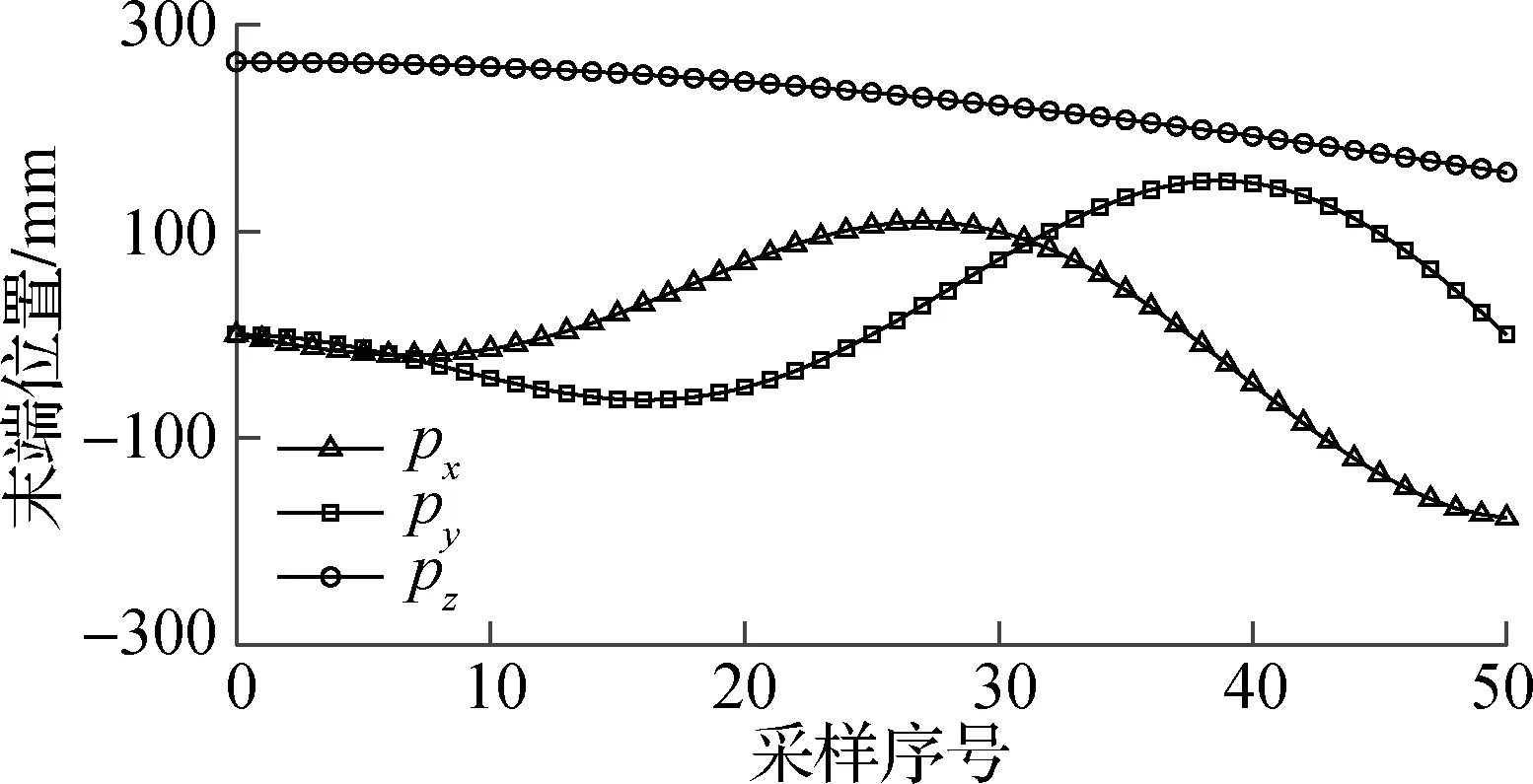
(a) 类L形

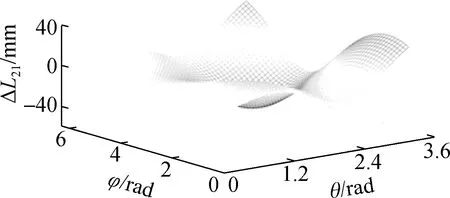
(a) 驱动线线长变化量ΔL21

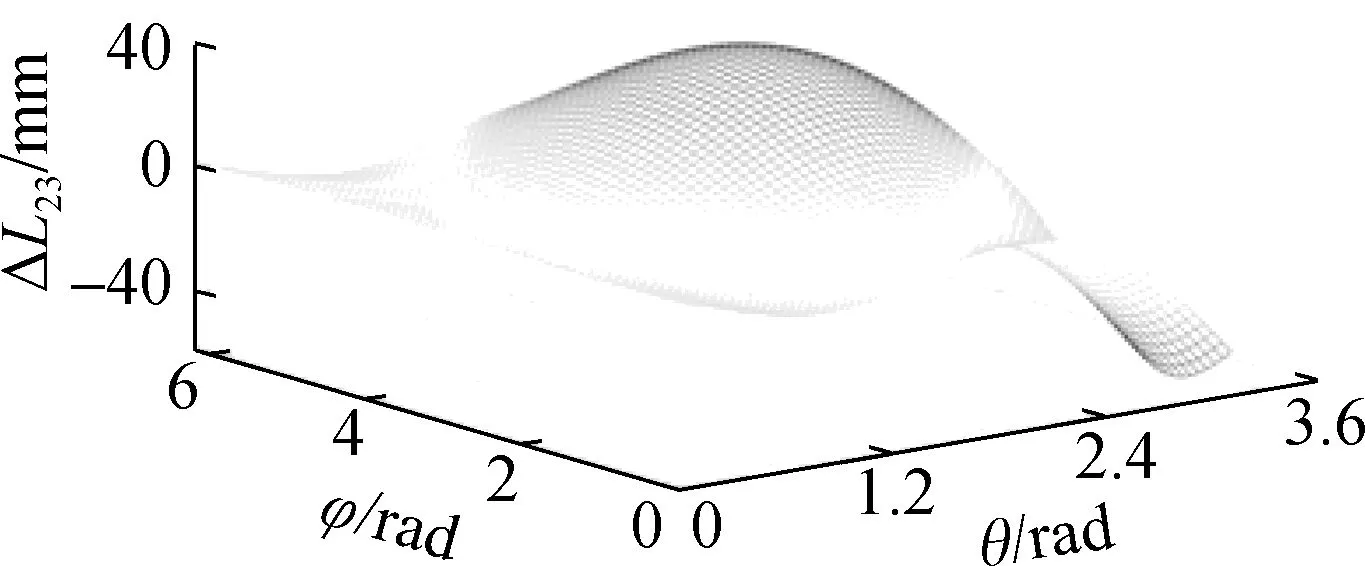
(c) 驱动线线长变化量ΔL23

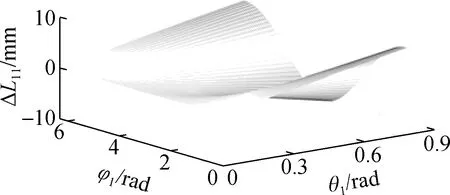
(a) 驱动线线长变化量ΔL11

(c) 驱动线线长变化量ΔL13

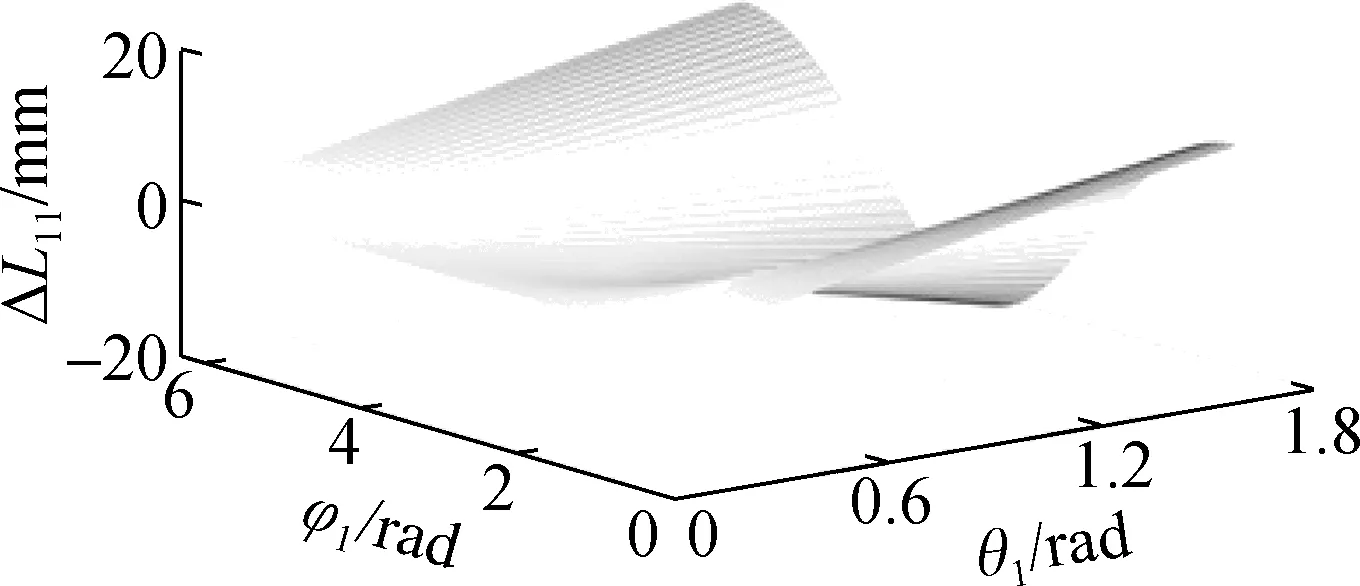
(a) 驱动线线长变化量ΔL11

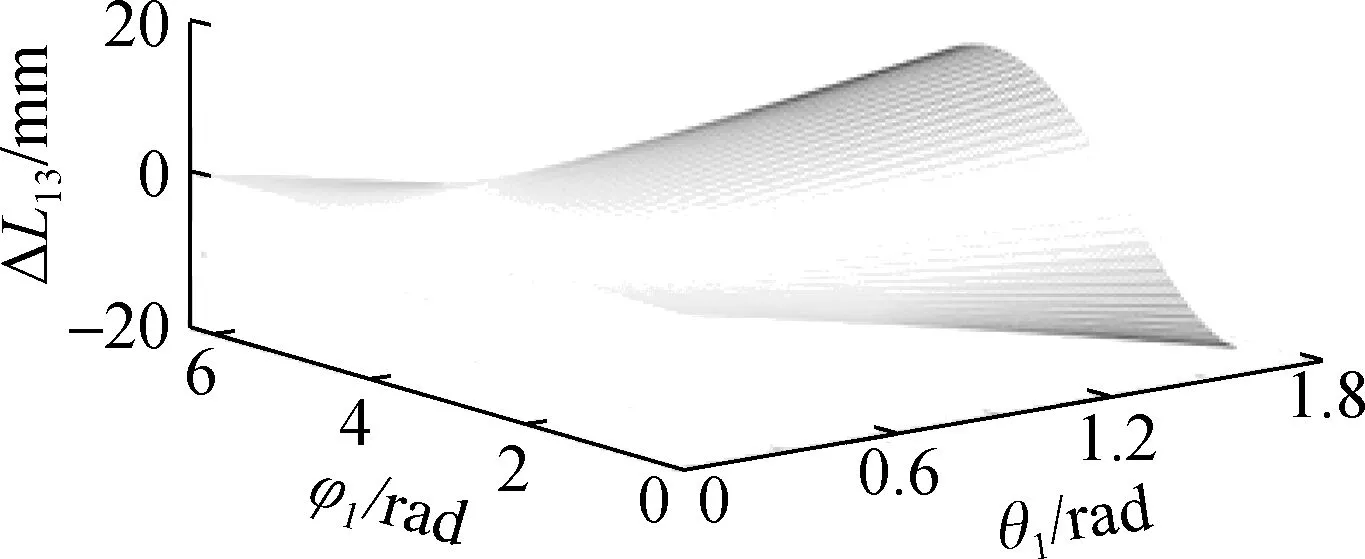
(c) 驱动线线长变化量ΔL13

4 结论

1) 结合仿生设计学在关节间引入万向节和圆柱螺旋弹簧约束进行经狭窄腔检测机器人的设计，在保证弯曲曲率恒定的前提下，可防止机械系统扭曲变形和轴向压缩变形.由万向节与内部传动轴交替连接构成柔性软轴，使得动力能从驱动端有效传输至机器人末端.

2) 基于几何分析方法，提出了一种线驱动连续型机器人单组关节单独运动和多组关节协同运动的运动学算法，建立了对应的几何模型和运动学模型，并对机器人单组关节工作空间进行了研究分析.在此基础上，推导出2组关节协同运动的解耦运动学算法，为多组关节协同运动的运动学解耦分析提供了定量分析手段.

3) 所提出的连续型经狭窄腔检测机器人具有较好的弯曲性能和通过能力，单组关节最大可弯曲180°；其工作空间大，单组关节最大作业半径为99.33 mm；能实现类L形、类S形的姿态变化，可满足对狭窄腔内目标进行大范围检测作业的需求.仿真结果表明，驱动线线长变化量曲面图的显示与其实际变化规律一致；由机器人末端位置变化曲线和驱动线线长变化量曲面可以看出，机器人整体运动平滑稳定，所建立的模型合理有效，为后续线驱动连续型机器人系统的研制奠定了理论和技术基础.