深化开放题教学 培养学生高阶思维

苏子沣

（闽清县白中镇中心小学，福建福州350806）

数学高阶思维“常发生在元认知、问题解决、应用与创造性活动中，学生的思维经历联系与转化、抽象与扩展、批判与监控的过程。”［1］教师培养学生的高阶思维能力是重要任务，也是课堂教学的重点问题。恰当应用开放题进行教学，有助于学生形成和发展数学高阶思维。小学数学开放题有条件开放题、方法开放题和结论开放题等。现以人教版小学数学教科书中开放题的教学为例，谈谈教师如何深化开放题教学，培养和发展学生的数学高阶思维能力。

一、经历联系与转化过程，用条件开放题培养学生高阶思维

条件开放题就是问题中所提供的条件太多、太少或隐含，导致学生无法直接根据已有条件解决问题。解决条件开放题，学生要根据题目中的所有数学信息进行分析、找出信息之间相互影响和相互制约的关系（即联系），并把题目中的信息根据需要进行适当变化（即转化），以便用所学知识顺利解决问题。学生通过观察、推理、联想、抽象或概括等思维过程排除多余条件、发现隐含条件，建立知识间的联系，对已有经验适当加工或改造，就能在问题解决的过程中发展数学高阶思维。

六年级下册P57有这样一道习题：用1:200的比例尺，画出你家房子的平面图。每个学生家的房子形状未必相同，所画的平面图也就可能大不一样。有的大，有的小。要画平面图，学生需要知道相关数据才行，但题中只有一个比例尺。仔细分析一下，学生可以发现题目中的隐含条件是这个图形最多只能是长为29.7厘米、宽为21厘米的长方形（A4纸大小）。教学时，教师要引导学生用整体的观点进行审题、找出隐含条件，发现这些信息中的联系，再根据比例尺1:200画房子的平面图，从而把实际问题转化为已知比例尺和实际距离求图上距离的数学问题。画图前，教师要引导学生实际测量房子的相关数据，再根据实际数据和比例尺算出图上的数据；画图时，教师要引导学生根据房子的造型构思图形，做到胸有成竹，再根据实际情况画图并及时修订，最后展示平面图、交流画图情况。

数学高阶思维要求学生能根据问题信息及时转换思路、把问题转化为新问题，而且要求学生能主动发现数学对象之间的相互联系。学生及时建立知识间的联系是问题转化的关键。数学对象之间建立的联系越丰富、越深刻，学生分析问题和解决问题时的思维转化就越灵活。学生把解决实际生活中的开放性问题所用的相关知识联系起来，使开放性问题转化为测量、计算图上距离等问题，实现对已有知识网络的整理和重组。学生对知识的联结越强，解决开放题越顺利，高阶思维的形成与发展就越有可能。

二、经历抽象与扩展过程，用方法开放题培养学生高阶思维

方法开放题就是学生要解决的数学开放性问题的方法并不唯一，而是多种多样。学生的不同思路可能会出现不同或相同的解题方法，学生的相同思路也可能会出现相同或不同的解题方法。学生可以从开放题的不同解题方法中抽取共性进行描述，从而形成正确认识（即抽象）；学生也可以从开放题最容易发现的方法开始思考，并扩大思维方向，以便从不同角度发现不同方法，直至举一反三地应用到类似问题解决过程中（即扩展）。解决方法开放题，学生要在抽象与扩展中透过现象看本质，发现、概括出一般规律，并进行知识的迁移、推广和应用，使学生在用不同思路解决问题的过程中发展高阶思维。

五年级下册P82有这样一道习题，要求填空：

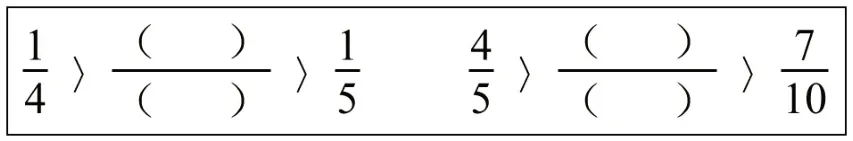
解决这道开放题时，有的学生通分，发现用20做公分母时，没有符合条件的分数；用40做公分母时，，符合要求的分数是；用60做公分母时，符合要求的分数是1360、1460（或730）……有的学生把分数化成小数，发现，介于0.2和0.25的两位小数有0.21、0.22、0.23、0.24，化成分数分别是介于0.2和0.25之间的小数有0.201、0.202、0.203、0.204……把这些小数化成分数，可以得到很多符合要求的分数。不同的解题方法，所用的知识不同，解决问题的过程也不同，学生的收获也不同，构建的问题解决模型不同，积累的解决问题经验也不同。学生可以把解决第一个问题所建构的数学模型和积累的相关数学活动经验迁移应用到第二个问题解决过程中。

培养学生的抽象思维是数学教学的共识，将经过抽象得到的数学知识进行广泛应用同样重要。“某种程度上，扩展也可看成是一种抽象，它是将抽象得到一般对象化到了更高的抽象层次。抽象思维与扩展能力相辅相成，共同为数学高阶思维领航”。［2］学生从不同角度思考问题，用不同方法解决问题，并在不同角度或方法之间进行灵活转化，最终殊途同归。当然，学生解决方法开放题需要辩证地看待不同方法之间的优劣，甚至可以适当进行方法比较与优化。

三、经历批判与监控过程，用结论开放题培养学生高阶思维

结论开放题的结论不确定，可以有多种答案。看问题的着眼点不同，探索出的结论可能也不同。学生需要根据已有信息探索符合条件的可能结论。如果学生对信息通过观察、比较、分析、综合、抽象、推理和概括并获得结论后，教师要引导他们学会批判和监控，也就是对已有结论要敢于质疑，帮助学生在识别、分析和评价结论中监控、调节思维过程。学生在批判和监控自己或同学的数学方法与数学结论的过程中能有效发展高阶思维。

六年级上册P93有这样一道开放题：

学生根据题目中的信息提出了一些数学问题，如：1.获二等奖的有多少幅？2.获三等奖的有多少幅？3.获三等奖的比二等奖多多少幅？4.获一等奖和二等奖的一共有多少幅？5.获一等奖和三等奖的一共有多少幅？6.获二等奖和三等奖的一共有多少幅？7.获奖的一共有多少幅？8.没获奖的一共有多少幅……交流时，学生对问题有了争议，焦点在获三等奖的人数究竟用125×16%×（1+4%），还是用125×（16%+4%）表示。教师引导持不同观点的学生进行辩论，他们分别阐述了自己的想法和理由：持前一种的观点学生认为，比较量是获二等奖的人数，4%是相对获二等奖的人数（即125×16%）而言的；持后一种观点的学生认为4%是相对125幅画而言的，并且指出如果用他们的方法，计算结果会出现小数，不符合生活实际情况。最后，持前一种观点的学生主动否定了自己的想法，支持了后一种观点。教师顺其自然地引导学生要灵活、准确地认识比较量，由此有效发展了高阶思维。