Hankel矩阵填充的保结构阈值修正算法
2020-12-21张春晓宋儒瑛
张春晓,宋儒瑛
(太原师范学院 数学系,山西 晋中 030619)
0 引言
矩阵填充是近些年以来非常热的一个研究课题,就是如何在不完备的数据下把缺少的数据补充完整.它的应用相当广泛,比如有图像修复、协同过滤等等.在这里主要研究图像修复问题.图像修复简单来说就是通过矩阵填充模型将“打码”的图片修复成原来的图片.通常使用的是由Candès和Recht[1]首先提出的凸优化问题模型
(1)
简单了解一下这个模型.‖X‖*是一个核范数,是所求矩阵X∈Rn1×n2的奇异值之和,是rank(X)的最优凸近似.{Mij:(i,j)∈Ω} 是秩为r的采样方阵M∈Rn1×n2里随机已知m个元素的集合,Ω是已知元素的下标集合.
现在用更通俗易懂的语言来描述一下研究内容:在现实生活中的大规模数据常常会有部分数据缺失、数据误差、损坏等问题,这将进一步加大数据处理和分析难度.这在实际生活中很常见.例如在人脸识别中,人的脸部在识别时会受到来自外界光照或是别的不可控因素的影响,导致识别到的人脸会有阴影、反光、扭曲等;在运动恢复结构问题中,提取和匹配特征值的时候,经常会存在较大的误差,这便会使得一些常规的分析方法和处理手段失效,所以需要提供一种更有效和更实用的算法能够为人脸识别技术提供强有力的理论支撑.并且,如果能够使得一些损毁、残缺的数据得到有效恢复,如果能够以正确的方法使数据变得完整,这些将会对大数据的建立、对数据的综合分析和处理产生更大效用.再比如一个“打码”的图片(就是失真的图片)用数学语言表示就是一个包含很多0元素的矩阵,每个0元素都是携带信息的,我们怎么样把0元素包含的信息挖掘出来呢?这就需要用到低秩了,这叫低秩矩阵重构问题.用一个简单的模型表述一下:已知矩阵是一个给定的M×N的矩阵A,其中一些元素因为某些原因丢失了,如果没有其他参考条件,我们确定这些数据很困难,但是我们已知A的秩是rank(A)≪M且rank(A)≪N,那么我们就可以通过矩阵各行(列)之间的线性相关将丢失的元素求出.
目前已经出现了大量的求解此问题的快速算法.比较著名的奇异值阈值算法(简称为SVT[2])、増广Lagrange 乘子算法(简称为ALM[3])、不需要奇异值分解的快速奇异值阈值法(简称为FastSVT[4])和加速奇异值阈值法(简称为ASVT[5])、正交秩1矩阵逼近法[6]、梯度投影算法[7]、交替最速下降算法(ASD[8])等等.
首先给出一个n×n的Hankel矩阵H∈Rn×n:
这个矩阵是由H=VDVT生成的,秩为r.这里V是一个n×r的范德蒙德矩阵,D是一个r×r的主对角矩阵.决定Hankel 矩阵的共有2n-1个元素,就是它的第1列和末1行.填充 Hankel 矩阵这个问题的研究价值极大,是一代代数学人薪火相传不断攻克的难关之一.之前Qiao等人演算出针对Hankel 矩阵的快速奇异值分解算法复杂度较小仅为O(n2logn),而一般矩阵的奇异值分解算法复杂度就较大为O(n3),两者之间的差距一目了然.Qiao等人这一算法的提出使整个数学界掀起了研究Hankel 矩阵的热潮.因为通过研究这一算法,大大减少了奇异值分解的时间,实现了很大的突破.众所周知,奇异值分解消耗的时间在矩阵的整体填充中拥有很大的占比.
填充方法的指向性不强是之前所有Hankel矩阵填充算法的关键所在,因此在该篇文章中主要解决这个问题并且提出了解决此问题的修正算法.这一修正算法吸收前人研究中的精华,并进行了严格的数值实验对比,最终证明了修正算法是卓有成效的.
本文结构安排:第2节简单回顾前人提出的基本算法,通过这些算法,Hankel矩阵问题将得到有效解决;第3节细致地介绍我们提出的l步修正的关于Hankel 矩阵的填充算法,并对新算法进行实验验证;第4节是对全文的总结.
下面是一些相关的定义:
定义1设任意矩阵X=(xij)∈Rn×n,E(X) 定义如下:
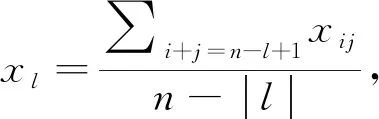

定义2(奇异值分解(SVD)) 矩阵X∈Rn1×n2,秩为r,一定存在某个正交矩阵U∈Rn1×r和V∈Rn2×r,使得:
X=U∑rVT,∑r=diag(σ1,…,σr),
其中:σ1≥σ2≥…≥σr>0.
定义3(奇异值阈值算子) 对于任意参数τ≥0,秩为r的矩阵X∈Rn1×n2,存在奇异值分解X=U∑rVT,奇异值阈值算子Dτ定义为:
Dτ(X):=UDτ(∑)VT,Dτ(∑)=diag({σi-τ}+)
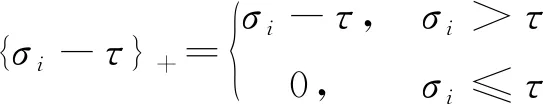
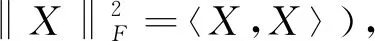

表示一个n×n矩阵,其中l=-n+1,…,n-1.PΩ是集合Ω上的正交投影满足:
1 算法回顾
出于文章的完整性考虑,先做一些简单回顾.
下面的优化模型为低秩状态下Hankel矩阵的填充问题:
(2)
X、M均为Hankel矩阵,并且M是低秩,Ω⊂{-n+1,…,n-1}
Hankel 矩阵是拥有特殊结构的,我们在对其进行填充时,使得每次迭代得到的填充矩阵都保持了Hankel 结构,而利用好快速奇异值分解就是利用Lanczos方法和快速傅里叶变换技术.
算法1矩阵填充的奇异值阈值(SVT)算法
奇异值阈值法是如下的优化模型:
(3)
其算法如下:
第一步: 给定Ω为下标集合,PΩ(M)为样本矩阵,参数τ,步长δ,误差ε,以及初始矩阵Y0=k0δPΩ(M),k:=0.
第二步: 计算矩阵YK比阈值τ大的SVD
[Uk,∑k,Vk]=lansvd(Yk)
令Xk+1=UkDτk(∑k)VkT.
第三步: 若‖PΩ(Xk+1-M)‖F/‖PΩ(M)‖F≤ε,停止; 否则,转第四步.
第四步:Yk+1=PΩ(Yk)+δPΩ(M-Xk+1);
算法2矩阵填充的增广拉格朗日乘子(ALM)算法
增广拉格朗日乘子法是如下的优化模型:
(4)
其拉格朗日函数为:
其中Y∈Rn1×n2,其算法如下:
第一步: 给定参数μ0>0,p>1误差ε1和ε2,给定样本矩阵PΩ(M),初始矩阵Y0=0,E0=0,k:=0.
第二步: 计算矩阵YK比阈值μk-1大的SVD
[Uk,∑k,Vk]μk-1=svd(D-Ek+μk-1Yk)
第三步:令
Ak+1=UkDμk-1(∑k)VkT
第四步: 若‖D-Ak+1-Ek+1‖F/‖D‖F<ε1,且μk‖Ek+1-Ek‖F/‖D‖F<ε2停止,否则转第五步;
第五步: 给定参数,令Yk+1=YK+μk(D-Ak+1-Ek+1),如果μk‖Ek+1-Ek‖F/‖D‖F<ε2,
令μk+1=ρμk;否则,应该转第二步.
算法3
基于F-模的Hankel 矩阵填充的保结构阈值算法(structure-preserving thresholding algorithm based on F-norm for Hankel matrix completion,简称 F-NSPTA)
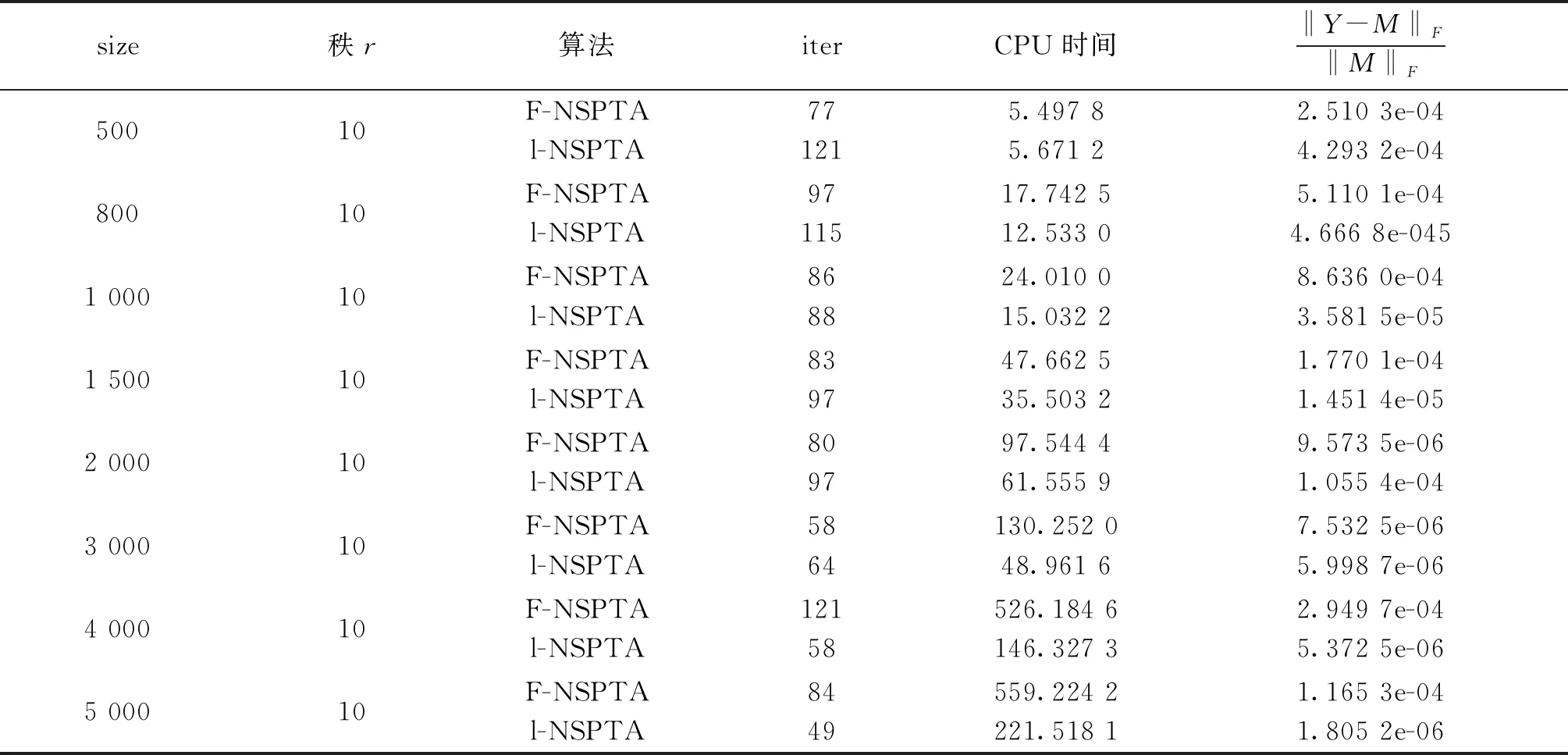
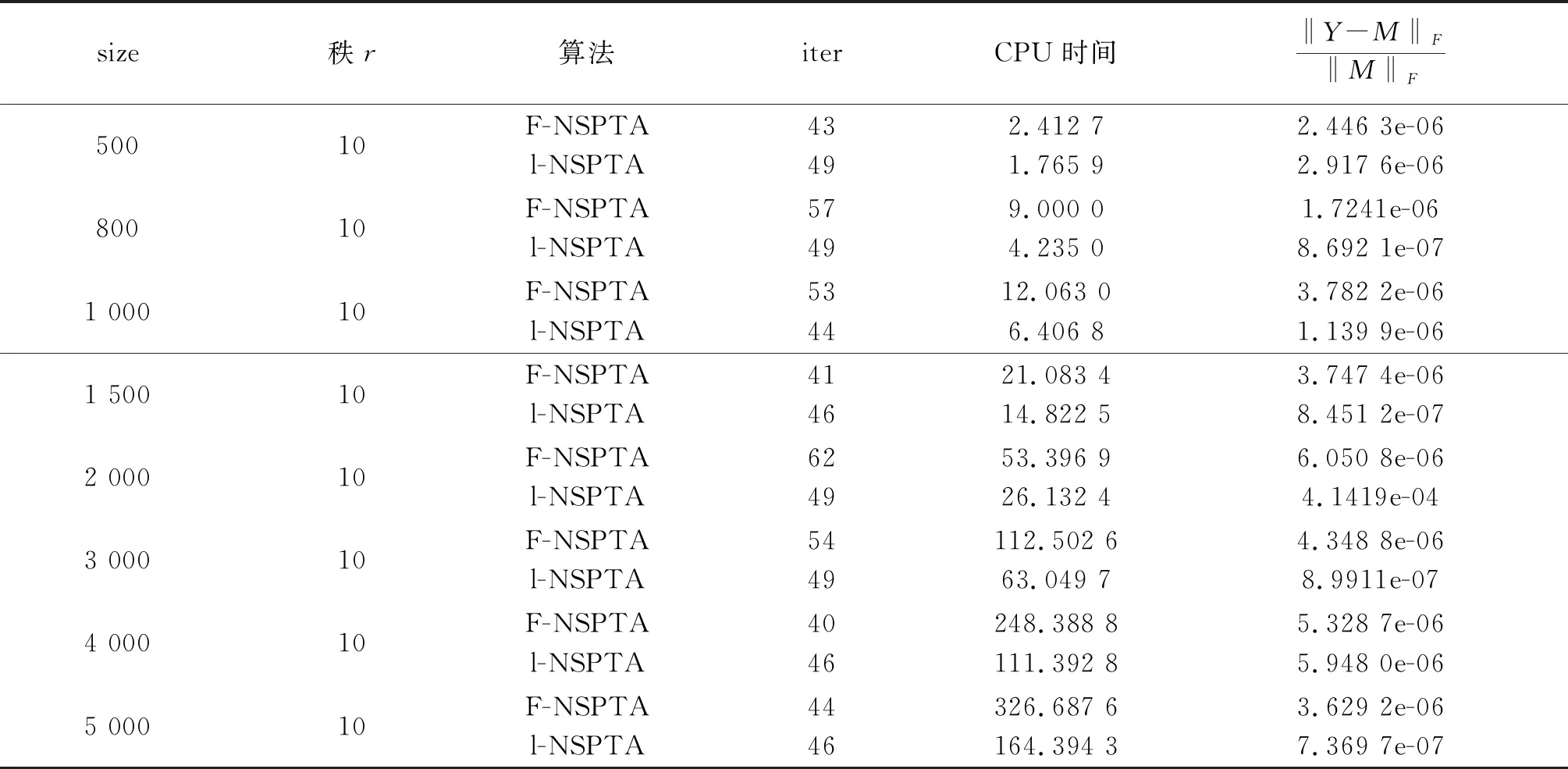
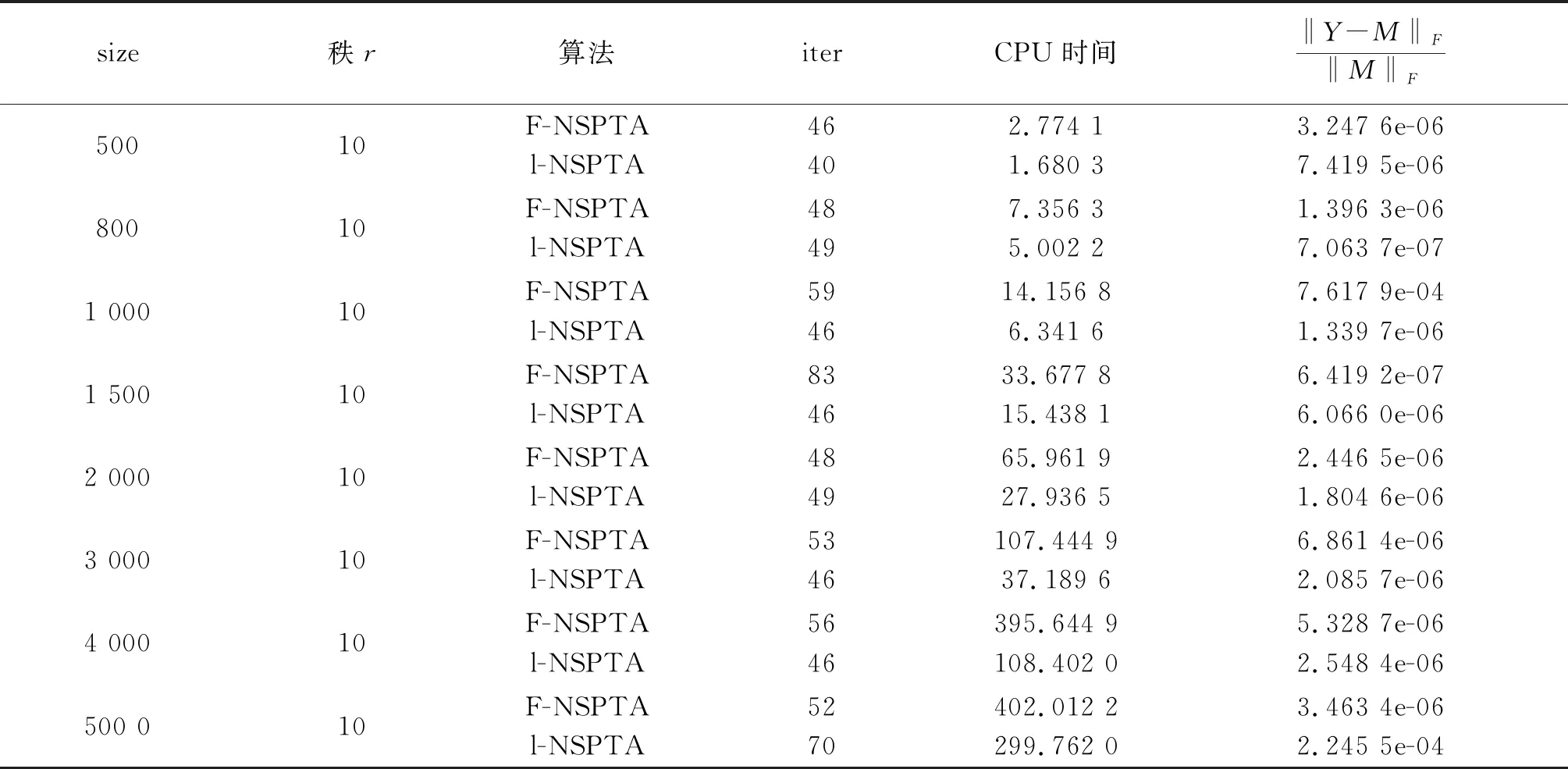
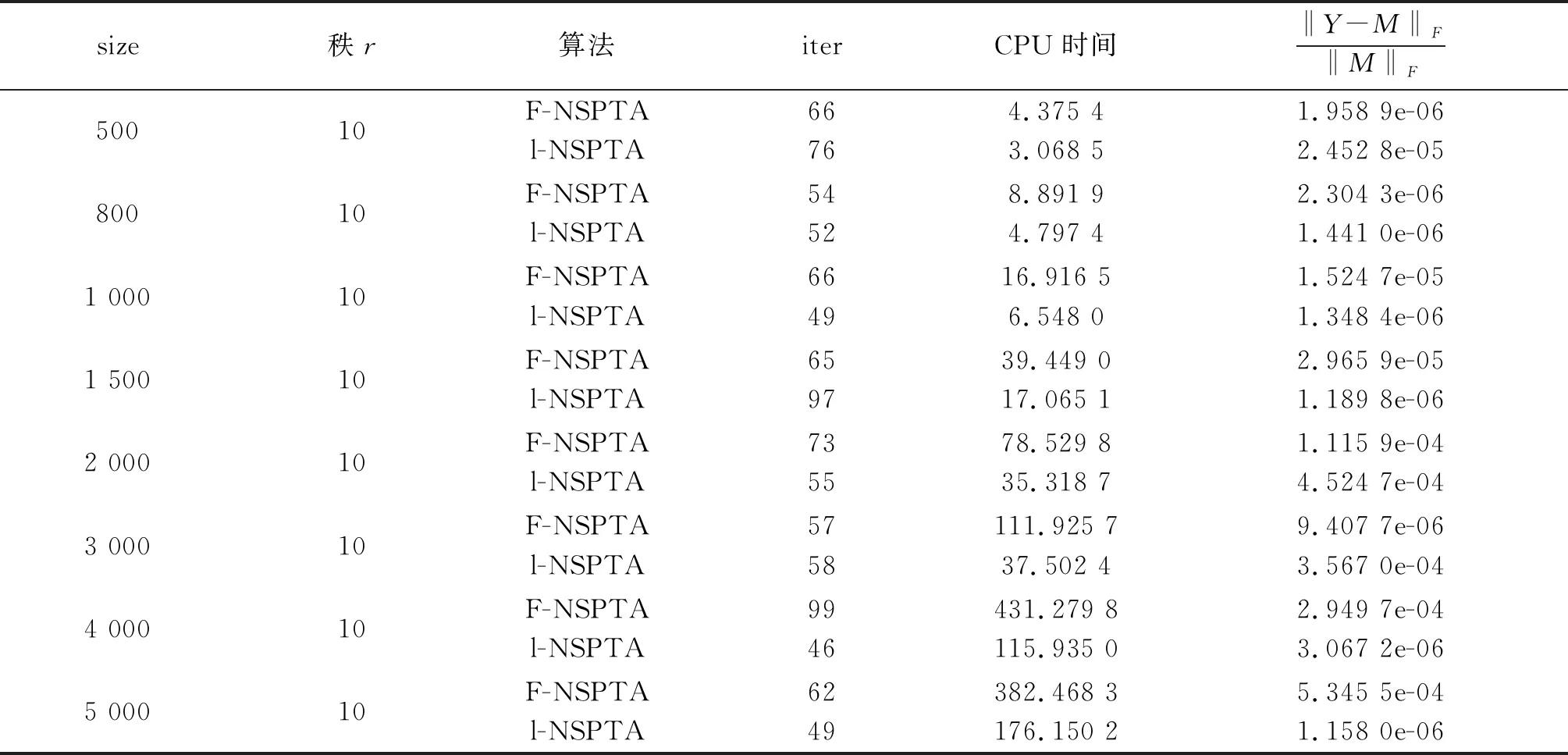
第一步:给定Ω为下标集合,PΩ(M)为样本矩阵,参数τ0,0 第二步:计算矩阵YK比阈值τk大的奇异值 [Uk,∑k,Vk]=lansvd(Yk) 令 第三步,计算 第四步: 给定参数,若‖Yk+1-Yk‖F/‖Yk‖F<ε, 就停止 ; 否则改变参数τ,选择τk+1使满足 ‖Yk+1-Xk+1‖F≤‖Yk-Xk‖F,转第五步. 第五步: 给定参数k:=k+1,转第二步. l步修正的Hankel矩阵填充的保结构阈值算法(structure-preserving threshold algorithm for L-Step modified Hankel matrix completion,简称l-NSPTA) 第一步:给定Ω为下标集合,PΩ(M)为样本矩阵,参数τ0,0 第二步:前l-1步迭代 1) 计算矩阵YK,q比阈值τk,q大的奇异值 令 2) 计算 Yk+1,q+1=Xk,q+PΩ(M). 3) 给定参数,若‖Yk+1,q+1-Yk,q‖F/‖Yk,q‖F<ε,就停止;否则改变参数τ,选择τk+1,q+1使满足‖Yk+1,q+q-Xk+1,q+1‖F≤‖Yk,q-Xk,q‖F. 第三步:第l步迭代 1) 计算矩阵YK,l比阈值τk,l大的奇异值 令 Xk,l=Uk,lDτk,l(∑k,l)Vk,lT. 2) 计算光滑算子 第四步:给定参数,若‖Yk+l-Yk‖F/‖Yk‖F<ε, 就停止;否则改变参数τ, 选择τk+1使满足‖Yk+l-Xk+l‖F≤‖Yk-Xk‖F,转第五步. 第五步:给定参数k:=k+1,q:=q+1,转第二步. 很明显,此算法是F-NSPTA算法的加速算法,如果l=1时就等同于F-NSPTA算法. 注:采样矩阵M产生的Hankel矩阵都是随机的,未知元素的位置都是不同的,这就会导致个别实验时间的波动. 表1 p=0.2 表2 p=0.3 续表2 表3 p=0.4 表4 p=0.6 表5 p=0.6 经过全新修正之后的奇异值阈值算法,是更好的填充算法.经过两种算法的比较之后,可以发现我们提出的步修正算法具有更好的收敛性及更高的精准度.总的来说,采样率与计算时间是成反比的.2 新算法及数值实验
2.1 新算法
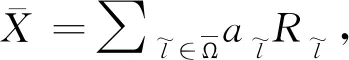
2.2 数值实验

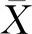

3 总结
