国家数值风洞(NNW)通用软件同构混合求解器设计

陈坚强, 马燕凯, 闵耀兵, 赵 钟, 何先耀, 何 琨

(中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000)

0 引 言

计算流体力学(Computational Fluid Dynamics，CFD)，是当前飞行器设计过程中，用以获得气动数据的重要手段，已从早期的仅用于校验辅助设计，发展到能为设计包线中的部分状态直接提供气动数据。然而，尽管近二三十年来，CFD发挥的作用在持续增加，但计算结果可信度仅局限于无大分离流动的巡航状态(图1)[1]，而在飞行包线的边缘区，仍然存在较大的不确定度。

图1 CFD在飞行包线中发挥的作用[1]

造成此种窘境的关键因素之一，在于当前使用“单一”的CFD方法模拟“复杂”的非线性流动：(1)单一的网格类型。不管是广泛使用的In-House代码，还是通用商业CFD软件，都采用单一的网格类型，要么是基于结构网格、要么是基于非结构网格，相应的CFD求解器也只能是二选一。(2)单一的精度。当前工程中广泛应用的CFD软件，基本都是二阶精度，受限于高阶精度方法较低的健壮性，高阶精度方法还难以在工程中成熟应用。(3)单一的学科。大多是求解仅考虑空气动力学完全气体效应的流动模拟。(4)单一的物理模型。鉴于直接数值模拟方法(DNS)和大涡模拟方法(LES)的巨量计算资源需求，工程中一般采用全湍流的雷诺平均NS方法(RANS)。

然而，现实中的空气动力学却是“多元”的：(1)多元的网格。相对结构网格，虽然因非结构网格生成难度的降低而应用越来越多，但在高超声速、高精度等对网格质量要求较高的领域，由于结构网格具有计算效率高、对边界层的模拟更精确、易于处理各向异性网格等优势，依然有其存在的价值，二者仍将共存，且在各自领域发挥自身的优点。(2)多元的精度。当前，越来越多的高精度方法研究者意识到，即使在将来，高精度方法仍无法完全替代二阶精度方法，而是互补的关系。高精度方法在大分离流动、强间断等关键流动区域扮演关键角色，而二阶方法在巡航等常规状态模拟中具有较高的性价比。(3)多学科模拟。真实飞行环境中往往涉及“声、光、电、磁、热”等多学科耦合，单一的流体力学学科难以准确地模拟真实环境，毋庸置疑，未来的CFD必定是多学科耦合模拟。(4)多元的物理模型。由于复杂流动中伴随层流、转捩、湍流、大范围分离等多种流动，采用单一的湍流模拟方法要么性价比低，要么难以准确捕捉流场结构，而在不同区域采用不同的湍流模拟方法，是一种现实可行的求解策略。

采用“混合求解器”，是解决当前的“单一”化与“多元”化需求矛盾的有效途径之一。混合求解器，即在不同的区域，采用不同的求解器，发挥各自的优势，以实现有工程价值的复杂CFD模拟。例如，不同网格类型的混合求解，不同精度的混合求解，不同学科的混合求解。

早在20世纪90年代，就有研究者实现了结构/非结构网格的Euler混合计算[2]，应用于飞机外形，通过在两种类型网格的交界面上采用拼接网格，实现信息交换。2010年，研究者用混合计算方法模拟气动声学的多学科问题，在笛卡尔直角网格上采用有限差分法，在非结构网格上采用高阶间断有限元(DG)方法，以实现不大幅增加计算量的前提下，完成对复杂外形的高精度模拟[3-4]。知名In-House CFD代码elsA-Hybrid，原本是一款采用多块结构网格、基于有限体积方法的求解器elsA，为了充分利用结构网格高效高精度和非结构网格灵活性的优点，采用面向对象编程，在原有的结构求解代码基础上增加了非结构求解模块，开发了新一代混合求解器elsA-Hybrid[5-6]，实现了三维高升力外形、翼身组合体等外形的二阶混合模拟，两种求解算法尽可能做到代码的统一，例如在通量计算层次基本实现了代码统一，基本实现了在细粒度层面的混合求解。在空间计算域融合方面，在作为CREATE-AV子项之一的Helios软件系统中[7]，对旋翼类外形(图2)，Helios在空间中采用不同的网格类型离散，分别调用不同类型的求解器，如在外场空间笛卡尔网格上调用SAMARC求解器，在旋翼附近调用结构求解器OverFLOW，在机身附近调用非结构求解器FUN3D，不同的求解器之间通过Python实现数据共享。作者所在团队也在此前开展了结构/非结构混合计算相关研究[8-9]。

图2 Create项目中的多求解器混合计算[7]

对于混合计算技术，目前通常有两种不同的技术途径。一种是“异构”混合计算，以多求解器间松耦合为特征，如上面提及的CREATE中的Helios分系统；另一种是“同构”混合计算，以多算法在同一个平台上紧耦合模拟为特征，如上文提及的混合求解器elsA-Hybrid。“异构”混合计算能很方便地集成已有软件，开发成本低，风险小。但因各求解器之间数据结构不同，并行框架不相容，重复模块多，使其可扩展性、可维护性低。反之，“同构”混合计算是在同一个框架上开发，在数据结构、并行框架等方面都可以大量复用，因而效率高、可扩展性、可维护性强。但因需统一多种求解器，因而风险大、工作量大、难度大。“异构”混合计算模式适用于集成存量，而“同构”混合计算是一种面向下一代的CFD软件的挑战性模式。

“国家数值风洞(NNW)”是我国正在自主研发的CFD软件系统，目标是建设国际领先的CFD高性能计算机系统，建成拥有自主知识产权、国内开放共享、达到世界一流水平的空气动力数值模拟平台。“风雷(PHengLEI)”软件[10-11]，是NNW工程的通用CFD软件，设计了面向结构/非结构的、适用于大规模并行的软件架构，其典型特色是可实现任意求解器的“同构”混合计算，以解决未来多学科模拟中对“多元”化CFD模拟的需求。

WCNS高阶精度有限差分方法由邓小刚等人提出[12]并经过二十多年的持续发展，其对于流动结构的分辨能力较高[13]。在满足几何守恒律的基础上[14-15]，WCNS方法在复杂网格计算中的适应能力得以大幅提升。近年来，在全局守恒条件约束下，邓小刚等人又发展了与内点相匹配的WCNS边界计算方法[16]。当前制约WCNS高阶方法应用于工程复杂外形流动计算的主要难点在于高质量的多块对接结构网格的生成，以及复杂边界处理，其直接影响到计算鲁棒性，是制约工程应用推广的瓶颈。

本文就PHengLEI软件中的混合求解器，介绍了混合求解策略及软件设计方法，并通过典型算例，验证结构/非结构网格耦合求解、二阶有限体积/WCNS高阶耦合求解这两类混合求解方法的可行性。有关PHengLEI软件的整体架构、并行方法，可参考文献[10-11]。

1 域、交界面与数据交换

在正式介绍混合计算策略前，先介绍与混合计算紧密联系的一些概念(如域、交界面)，以及相关的数据结构。

1.1 域和交界面的抽象

CFD模拟一般基于计算网格进行，整个计算域由多个计算区域组成，每个计算域被离散为若干网格单元。采用结构网格时，首先用线、面将整体计算域划分为多个子域，再在每个子域生成网格单元。采用非结构网格时，虽然初始整体计算域作为一个整体存在，但是在并行计算时，一个计算域被分解为多个子域。我们将每个子域及其所属的网格单元，定义为域(Zone)，不同域之间的交界面，定义为交界面(Interface)。图3的示例中，整个计算域被划分为2个域，Zone1和Zone2，为示普遍性，分别为非结构和结构网格，二者间是互不重叠且对接(点一一对应)的交界面。

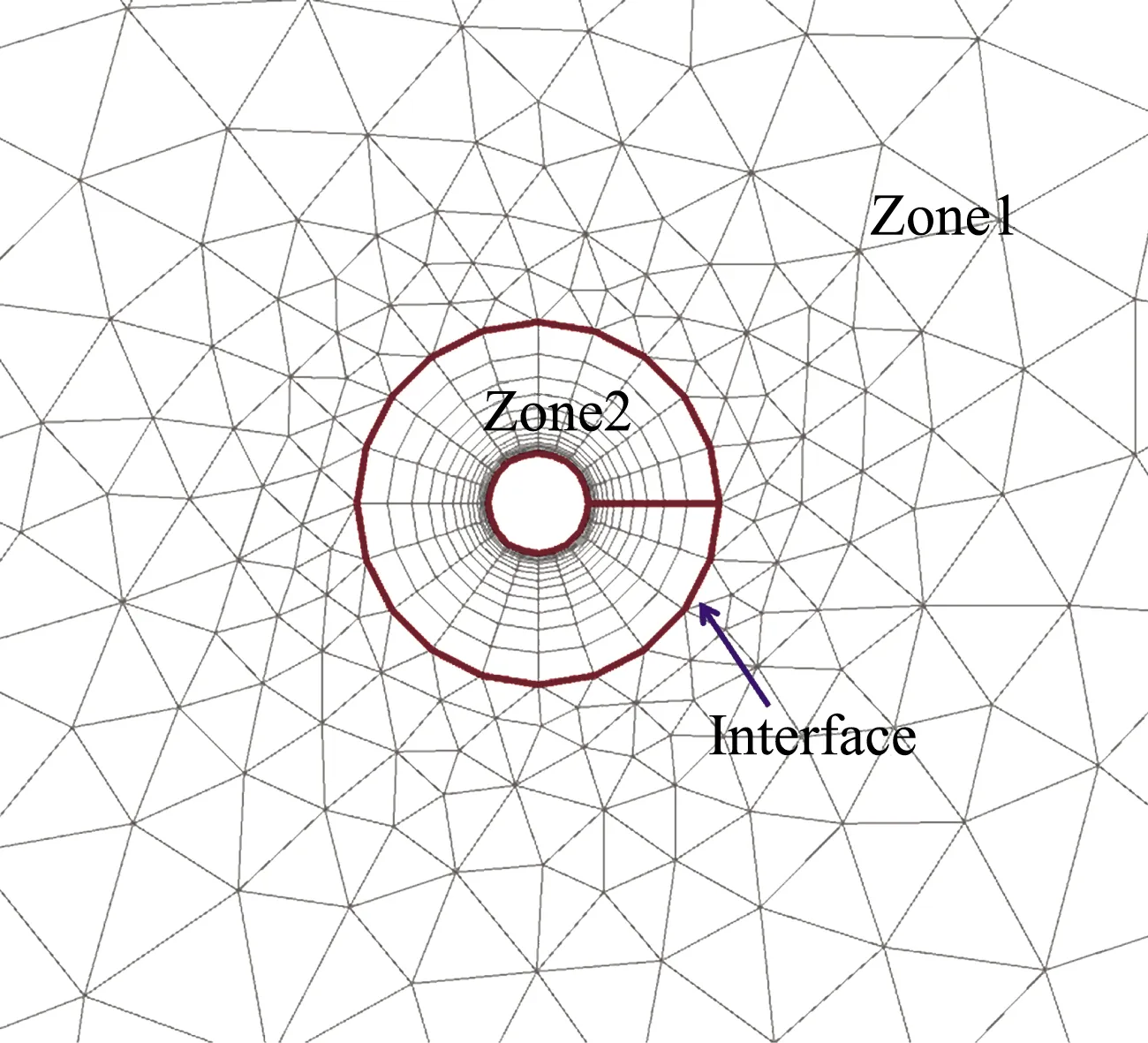
图3 域与交界面

域，是混合计算中不同求解器的载体。在混合计算时，将在每个域上存储各自的求解器。在每一迭代步中，遍历所有的子域求解。

交界面，是混合求解器的核心。不同域(其上可能加载不同的求解器)间的数据交换，通过交界面实施。实际上，这里的交界面是广义的，包含三种类型：

1)多块结构网格中，块与块之间的交界面；

2)非结构网格中，并行计算分区后，分区之间的交界面；

3)在计算域中同时含有结构、非结构网格时，两种网格类型间的交界面。

混合求解，即是每个交界面两侧的两个单元(分别是结构、非结构网格单元)交换流场数据，进而实现不同域之间耦合的过程。

1.2 数据结构与信息交换

PHengLEI软件中定义的“交界面”是以上三种类型的合集，即将三种交界面抽象为统一的“Interface”。无论是何种类型，都采用相同的数据结构存储、交换。因之，交界面的数据结构是核心。

为此，风雷软件中设计了“三合一”的数据底层DataContainer，用于交换网格块间的各类数据。任意数据经DataContainer标准化为数据底层后，在完全相同的机制下实现以下“三合一”数据交换：

a)进程内的结构多块网格交界面数据交换；

b)进程间的相邻网格块(既可以是结构，也可以是非结构)交界面数据交换，主要用于MPI通信；

c)节点内任意网格块交界面数据交换，主要用于混合求解器计算。

数据标准化的原理很简单：对于结构、非结构两种不同的数据存储结构，将二者统一压缩为字符型数据，以实现两类数据的标准化[10]。

2 混合求解策略

下文以结构/非结构混合计算、二阶/高阶混合计算，说明混合求解器的耦合策略。

2.1 结构/非结构耦合策略

PHengLEI软件框架既适应于结构网格、非结构网格，还能实现结构/非结构网格下的求解器耦合计算。结构/非结构两种求解器可独立运行(即在流场中同时含有结构网格和非结构网格的情况下，在结构网格上调用结构求解器，在非结构网格上调用非结构求解器)，并能进行结构求解器和非结构求解器的同步耦合计算。

结构/非结构耦合计算的关键技术是两种类型网格交界面的数据通信。在两种网格内部分别调用结构/非结构求解器计算，两种网格间的交界面形成各自求解器的边界条件，将这种边界条件抽象为InterFace类。在结构网格和非结构网格之间，通过交界面建立一一对应的面映射关系(图4)，计算模板相应扩展：对于结构求解器，在内场单元i处将另一侧的非结构网格体心值视为其虚拟单元(i+1)；对于非结构求解器，在内场单元le处将另一侧的结构网格体心值视为其虚拟单元(re)。对于结构求解器，往往需要在边界处拓宽虚拟单元模板，除了i+1点外，还需要i+2，……，i+n点信息，为简便起见，混合计算时一般采用一层虚拟单元。

(a)结构求解器模板 (b)非结构求解器模板

结构/非结构网格交界面InterFace的处理方式和并行分区交界面、多块结构网格间交界面完全一样，采用“三合一”数据底层进行数据交换。在计算过程中，通过交界面交换流场变量q和梯度q。

2.2 二阶/高阶精度耦合策略

PHengLEI软件框架中，二阶/高阶精度耦合策略是指，二阶精度求解器采用结构或非结构的有限体积方法，高阶精度求解器采用基于结构网格的WCNS高阶精度有限差分方法。研究表明[17]，WCNS求解器分辨率较二阶有限体积求解器高，对关键流动结构的模拟能力明显优于传统的二阶求解器。但WCNS高阶精度计算方法对网格质量要求较高，其适应复杂外形计算的能力不如非结构网格的二阶求解器。二阶非结构解算器适用于复杂外形计算，但不具备WCNS高阶精度求解器对流场结构的分辨率。因此，从WCNS求解器工程实用化观点看，在关键流动特征区域采用高质量的结构网格基于WCNS求解器计算，而在其他复杂区域采用非结构网格基于二阶精度非结构求解器计算，使高阶精度结构求解器和二阶精度非结构求解器优势互补，不失为一种解决工程实际复杂问题的可行方案。

二阶/高阶精度求解器耦合策略与结构/非结构耦合策略相同，都是交换流场变量、梯度等(图5)。

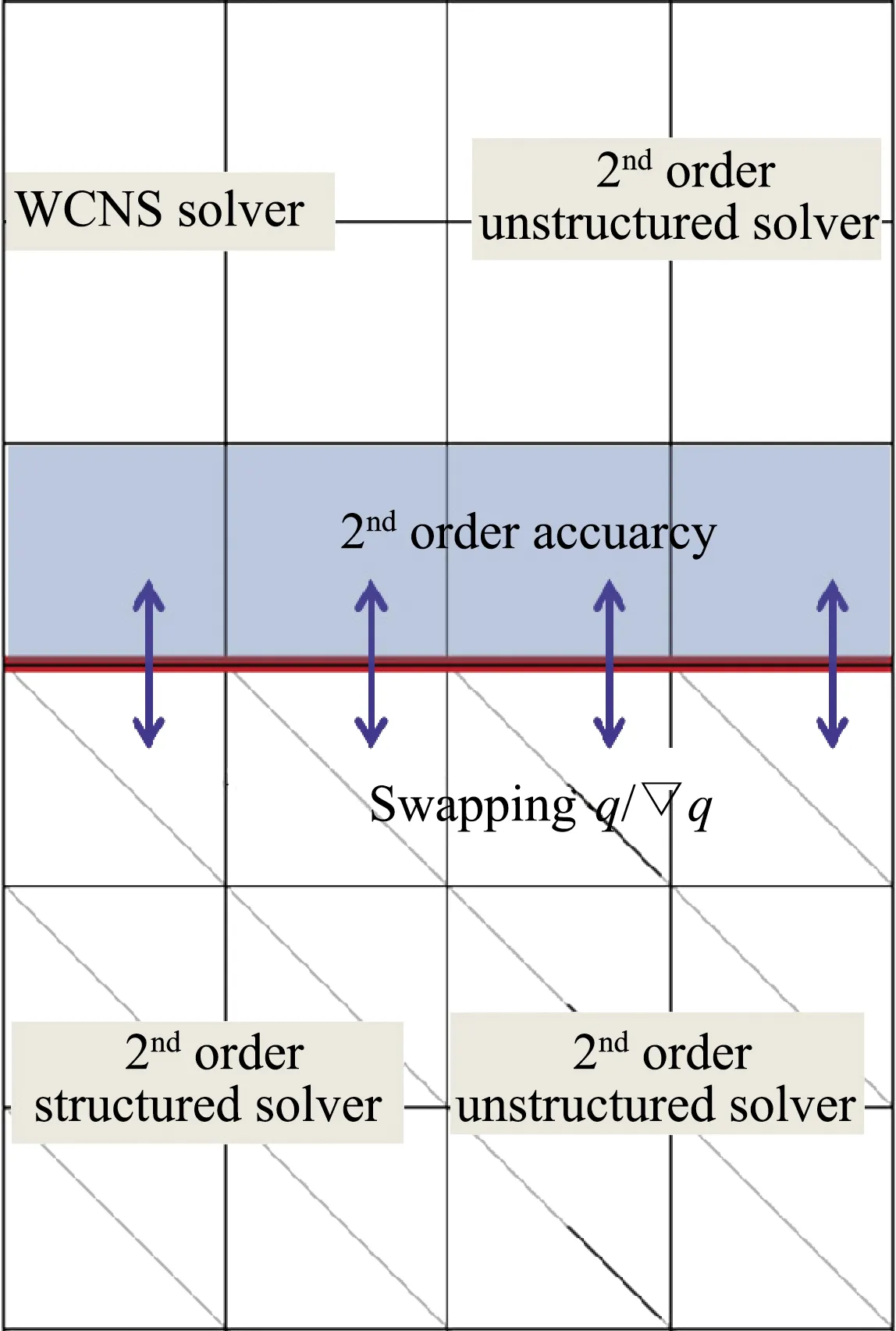
图5 混合求解器信息交换

单一的WCNS求解器应用于多块网格时，需根据精度的需要，交换紧邻交界面的多层单元数据(三阶精度需交换2层)。很显然，非结构网格中由于没有网格层，只向WCNS求解器提供1层信息，相当于在交界面处退化为二阶精度。实际上，对于混合求解器来说，在非结构网格上已经全部是二阶精度，即使在结构网格上有1层网格精度退化，也无大碍。

3 混合计算案例

为考察本文混合求解耦合策略的有效性，以二维圆柱和三维双椭球的高超声速黏性绕流为例，对二阶非结构/二阶结构混合计算、二阶非结构/高阶WCNS混合求解方法可行性与正确性进行验证。

3.1 二维圆柱绕流

计算条件[18]：层流，来流马赫数8.03，来流单位雷诺数1.835×105，来流温度124.94 K，壁面温度294.44 K。采用三套网格(图6)进行计算：第一套为结构网格，网格数目为121×87(流线×法向)，采用结构WCNS高阶精度求解器；第二套是混合网格，将第一套网格划分为内外两个块得到，靠近壁面的是结构网格，采用WCNS高阶精度求解器，远离壁面的结构网格被非结构化，采用二阶精度非结构有限体积求解器(Unstr-FVM)；第三套是混合网格，将第二套网格中外场块四边形网格三角化得到，内场结构网格上依然采用WCNS高阶求解器，外场三角形网格采用Unstr-FVM求解器。

图6 二维层流圆柱算例的网格分布及各区域所加载的求解器示意图

这三套网格(三种计算策略)的目的是：第一套网格是全高精度计算，用于对比参考；第二套网格与第一套相同，仅仅是将四边形非结构化，用于比较混合求解器带来的差异；第三套是混合网格、混合求解器，是测试的目的。

从计算收敛性看(图7)，三套网格残差均收敛至机器“零”，且收敛后的气动力系数保持一致。从物面压力和热流分布看(图8)，三套网格上的结果几乎重合，混合计算与全结构网格WCSN高阶精度模拟结果相差无几。该算例表明，混合计算既能保持高精度格式的方法，又适应非结构网格。

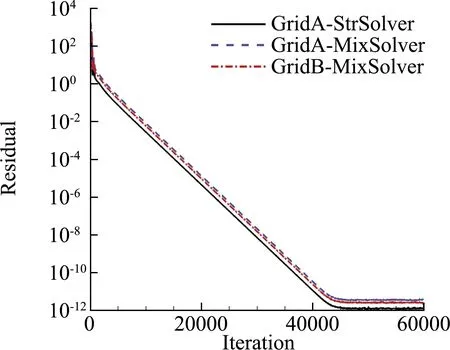
(a)残差

(a)壁面压力分布

3.2 双椭球绕流

双椭球绕流是典型的高超声速模拟算例[19-21]。计算条件为：层流，0°攻角，来流马赫数8.15，来流单位雷诺数1.67×107，来流温度56 K，壁面温度288 K，不考虑底部流动。采用两套网格计算(图9)：第一套为纯结构网格，根据流场特点对强激波、激波与边界层干扰、激波与激波干扰的区域进行了局部网格加密，网格总数为468万，运行WCNS高阶精度求解器；第二套是结构/非结构混合网格，壁面附近为结构网格，运行WCNS求解器，远离壁面区域为非结构网格，运行二阶精度非结构有限体积求解器(Unstr-FVM)。

(a)纯结构网格

从残差收敛看(图10)，WCNS/FVM混合求解器能保持纯WCNS高阶求解器的收敛性。图11是两种求解器计算所得的表面极限流线，混合求解器保持了WCNS高阶求解器对二次分离流的清晰捕捉能力。

图10 混合求解器与纯高阶求解器残差收敛对比

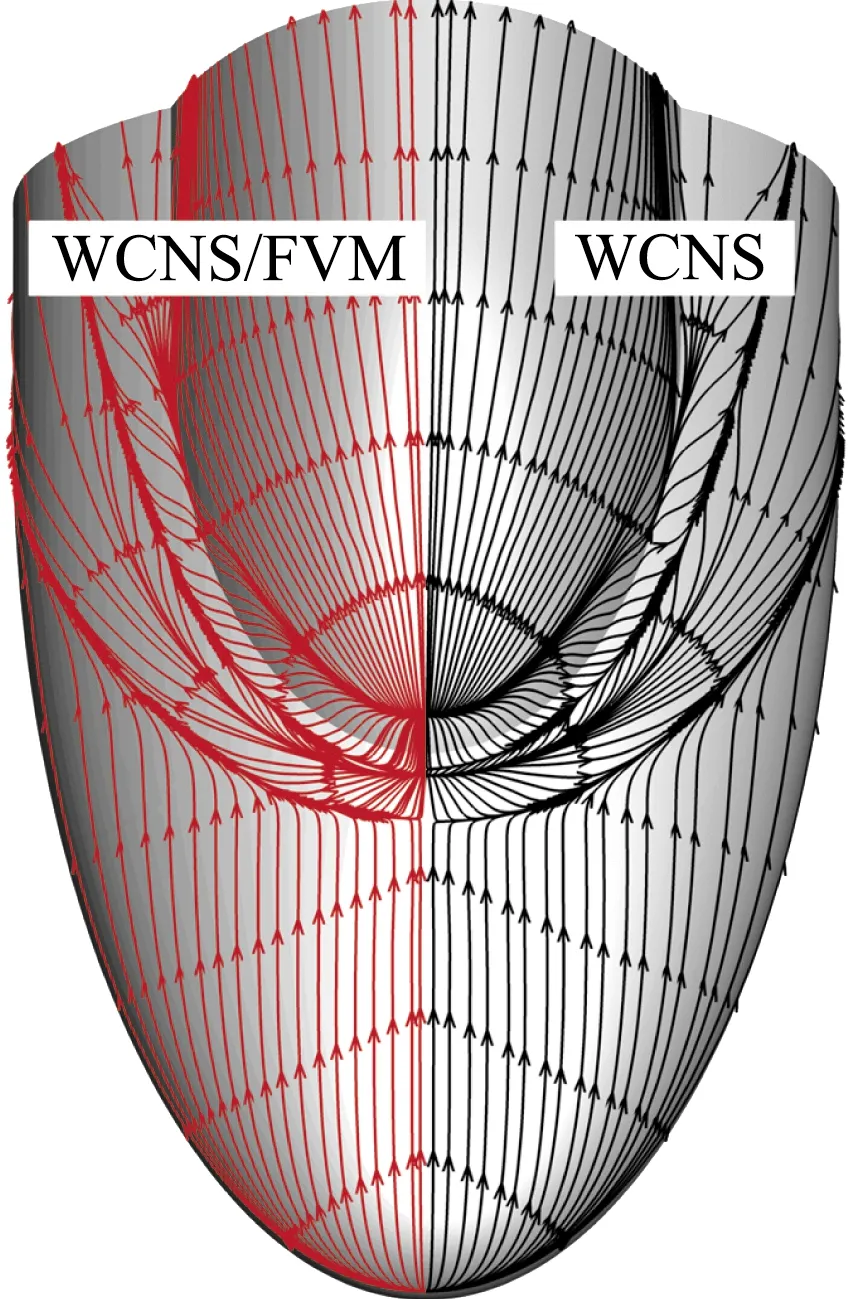
图11 混合求解器与纯高阶求解器极限流线对比

从物面的压强和热流分布看(图12)，两种求解器计算得到的压强分布与试验数据有很好一致性，流经第二椭圆之后，压力与热流均显著上升，达到峰值。同样地，该算例表明了，在三维情况下，混合求解器仍然能保持高精度方法的特性。

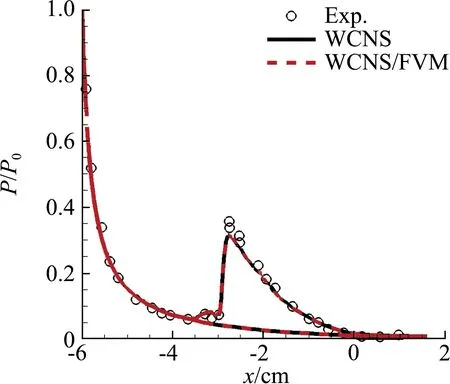
(a)对称面压力分布

3.3 混合求解器效率比较

之所以发展“同构”混合求解，原因之一是其能吸收结构求解器的高效率优点。对上述两个算例，对比分析了结构、非结构、混合求解三种策略的计算效率。对每个算例，三种策略都采用同一套结构网格，非结构求解器将其全局非结构化计算，混合求解器将外场部分非结构化计算。

在保证计算稳定收敛的前提下，三种策略均采用最大CFL数。在残差收敛曲线图中(图13、图14)，迭代步代表算法效率，墙上CPU时间则反应实际计算效率。从算法层面看(迭代步vs.残差)，结构求解器效率最高，混合计算次之，非结构最慢；从实际墙上CPU时间看，规律一样。即，兼顾了结构网格的计算精度和非结构网格的网格生成便利的混合求解策略，在计算效率上要优于完全的非结构网格计算。

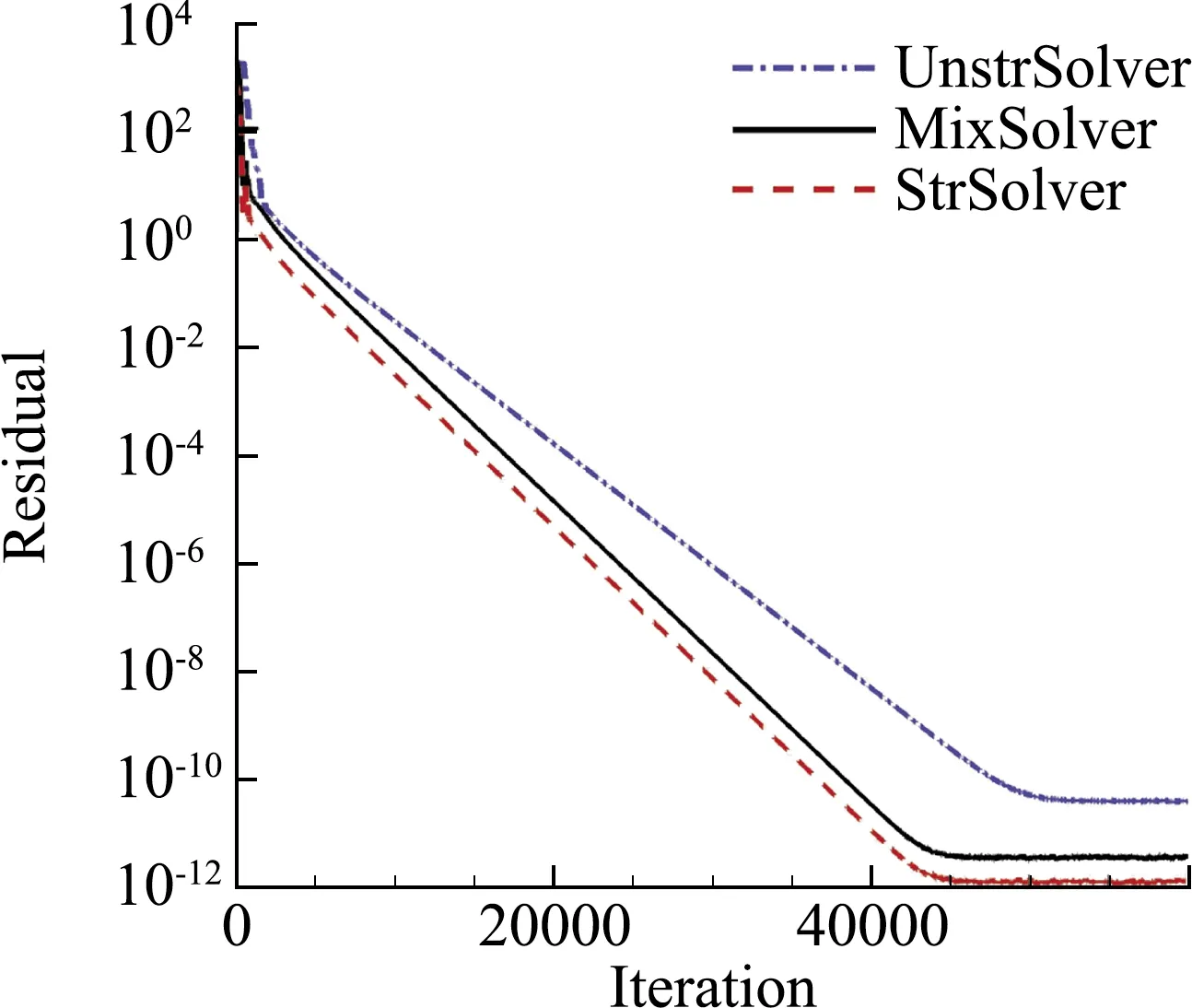
(a)残差收敛曲线(迭代步数)

(a)残差收敛曲线(迭代步数)

4 结 论

基于风雷软件，设计了“同构”混合求解策略，以及相应的交界面抽象方法、数据结构。作为“同构”混合计算的应用案例，以解决高阶精度方法的工程实用化为切入点，通过在结构网格上运行WCNS高阶求解器，在非结构网格上运行二阶有限体积(FVM)求解器，以达到在流动关键区域高阶模拟、在复杂区域非结构方便过渡的目的。

对二维圆柱和三维双椭球高超声速流动问题进行了模拟，结果表明，混合求解器能保持高阶求解器的特性，验证了风雷软件中区域混合计算策略的可行性，同时说明了混合计算的效率优势。

二阶/高阶混合求解的目标，是在对流动大范围分离、激波等典型特征处采用高阶方法，当前的工作仅是针对高超声速流动，在高超声速标模外形上进行的串行计算模拟，要实现在复杂外形上，高效、高精度模拟关键流动区域的最终目标，必须要实现混合求解器的并行化。风雷软件中纯结构、非结构求解器均有较强的并行可扩展性[10]，但要实现混合求解的并行计算，必须解决结构/非结构网格分区负载平衡问题。下一步，将着力解决求解器的并行化问题，以实现工程实用能力，为关键气动问题模拟提供技术支撑。

致谢:感谢国家数值风洞工程软件开发团队所有人员的付出和努力，感谢风雷(PHengLEI)软件前期开发者们的贡献，也感谢工程两委会的指导。