壁温对钝三角翼边界层稳定性及转捩影响

马祎蕾, 余 平, 姚世勇

(空间物理重点实验室, 北京 100076)

0 引 言

高超声速飞行器边界层流场发生转捩时，飞行器表面热环境及飞行器气动特性发生显著变化。正确预测转捩位置，对于优化飞行器热防护设计、提升飞行器性能具有十分重要的工程意义[1-2]。

影响高超声速边界层转捩的因素众多，包括转捩雷诺数、边界层边缘马赫数、壁面温度、攻角、头部钝度等[1-5]，且作用机理复杂，许多问题尚未解决。因此，高超声速边界层转捩是当前流体力学领域一个前沿和难点问题，受到广泛关注。

壁面温度是影响高超声速转捩的一个重要因素。通常情况下，地面风洞试验中壁温与来流总温比高，而天上真实飞行条件下的壁温与来流总温比低，地面试验无法模拟天上真实飞行的壁温条件，这是造成天地差异的一个重要因素。因此，研究壁面温度条件对边界层流动稳定性及转捩的影响十分重要。

Gary[6]研究表明，转捩雷诺数随着壁温比的降低而增大。Stetson[7]则通过热线试验发现，冷壁的转捩雷诺数(约3.2×106)低于正常壁温下的转捩雷诺数(约4.8×106)。Malik[8]采用eN法分析了5°尖锥的边界层流场稳定性特征，发现对于绝热壁边界层，在来流马赫数低于7时为第一模态导致转捩，而对于冷却壁，在较低马赫数时已变为第二模态导致转捩。Gasperas[9]研究分析了平板和尖锥在不同壁温下的稳定性特征，认为表面温度沿流向线性降低时，扰动增长率和N值明显小于绝热壁。尚庆等[10]研究表明，壁温升高会使壁面热流下降，速度边界层变厚，剖面不饱满，更易发生流动分离。苏彩虹、周恒[11]研究了0°攻角高超声速钝锥边界层，表明绝热壁边界层的转捩位置比等温壁边界层靠后。曹伟[12]研究发现，壁面温度条件对是第一模态还是第二模态波决定转捩位置有很大关系。刘志勇、杨武兵等[13]研究了一定来流工况下的平板边界层，发现壁温升高，初始推迟转捩，随后变化趋势发生反转。Liang等[14]研究了壁温对马赫数7.99的钝锥边界层流动稳定性影响，研究表明不同壁温比条件显著影响了边界层广义拐点和压力梯度分布，导致不同稳定性特征，同时在绝热壁条件下，扰动波增长不再只依赖于第二模态扰动波。王振清，唐小军等[15]研究表明，冷壁总体上加速了钝楔边界层高频不稳定模态的发展。Eppink等[16]通过对比试验和线性PSE结果表明，壁温对横流行波增长率影响很大，将显著改变N值分布。

以往关于高超声速边界层转捩壁温影响的研究多基于二维平板或轴对称的钝锥等简单外形，研究结果表明了壁面温度条件对转捩影响的复杂性。然而，对于采用升力体外形的高超声速飞行器来说，其三维几何特征明显，包括钝化的端头和翼前缘、大后掠角的翼面形状、较扁平的迎风面构型等。平板钝三角翼外形具有钝化的钝头、钝化的翼前缘、大的翼后掠角，有攻角下，其迎风面为简单的平板构型。显然，平板钝三角翼相比二维平板和轴对称钝锥更能表征升力体外形的高超声速流动，包括横流效应、前缘效应和熵层效应等，研究平板钝三角翼外形壁温条件对边界层流动稳定性及转捩的影响既具有学术价值，也具有工程价值。但是，对此类外形的相关研究工作很少，为此，有必要开展相关的壁温影响研究，为高超声速飞行器的转捩分析与预示奠定理论基础。

本文针对平板钝三角翼外形，围绕典型高超声速风洞试验状态开展流场数值计算和线性稳定性分析，研究不同壁温条件下该外形边界层的流动稳定性特征，并采用eN法获取不同壁温条件下平板钝三角翼表面的N值分布，研究壁温条件对边界层转捩的影响。

1 计算方法

1.1 控制方程

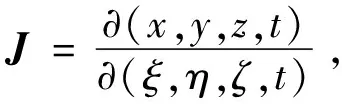
(1)

式中，

1.2 数值计算方法

N-S方程数值求解中，采用有限体积法，对流项采用三阶迎风Roe-FDS格式离散，黏性项采用中心差分格式离散，时间推进为AF-LU隐式方法。

不考虑对底部流场的模拟，物面采用无滑移边界条件，出口设为超声速外插边界条件。计算域为半模，网格量为201×281×137，如图1，法向网格布置点数较多，原因在于后续稳定性分析需要较为精细的边界层流场。

图1 计算域及网格

1.3 稳定性计算方法

根据线性稳定性理论，二维局部平行流假设下，分析O-S方程可将小扰动表示为行进波形式：

(2)

对于空间模式，式(2)中波数α、β一般为复数，其虚部的负值-αi、-βi分别为扰动在x向、z向的空间增长率，ω为扰动波频率。

扰动向下游传播时增长率将发生变化。目前工程上常用的一种转捩预测方法eN法[17-19]就是基于线性稳定性理论，将增长率沿扰动传播路径积分,得到扰动幅值放大因子N：

(3)

式中，(x0,z0)为频率为ω的扰动波开始失稳处(αi、βi由正转负的中性点)，其位置在中性曲线上；增长率-αi、-βi取当地频率为ω的最不稳定扰动波(增长率最大)的增长率，扰动传播路径方向即该扰动波的群速度方向。

预设转捩判据为Ntr(通常由经验给出)，即对于不同频率ω的扰动波，若在(xtr,ztr)处幅值放大因子达到Ntr，预示转捩发生。不同频率扰动波达到Ntr的位置不同，一般取最上游位置作为转捩发生位置，对应N值称为包络N值。转捩位置曲线应满足：

(4)

1.4 算例验证

文献[20]针对HIFiRE-1飞行工况进行了数值模拟，钝锥半锥角7°，头部半径2.5 mm，计算工况如表1，壁面条件取恒温壁Tw=410 K(Tw/T0,∞=0.168)。

表1 算例工况

为考核三维流场计算的可靠性，特别是边界层流场和横流效应，本文采用前述计算方法对文献[20]中算例进行了计算，得到的流向x=850 mm、背风面θ=135°位置点的基本流速度剖面与文献[20]结果比较如图2所示，其中橘色速度剖面为计算结果，与算例基本相符，验证了边界层流场计算的正确性。

(a)Streamwise velocity

2 几何模型与计算工况

几何模型为一平板钝三角翼外形[21]，长度取400 mm，钝度半径3 mm，后掠角75°。定义坐标系原点O为钝三角板顶点，x、z轴指向如图3所示，y轴符合右手坐标系。

图3 平板钝三角翼外形及坐标系示意图

基本的计算工况选取典型的地面高超声速风洞试验条件：单位来流雷诺数Re∞=7.12×106/m，马赫数M∞=6，总温T0,∞=420 K，攻角、侧滑角均为0°。选取壁温条件时，考虑了以下四种典型情况：

1)/真实飞行状态下，来流总温高，壁温比小，约为0.3；2)在飞行器再入段，由于前期的气动加热和随后的飞行速度降低，有些情况下会出现真实壁温高于绝热壁温的情况，即壁面向流场放热，此时壁温比很高，超过绝热壁温比；3)高超声速风洞试验中，来流总温较低，壁温比通常为0.7左右；4)在温敏漆等试验中，由于采用非金属材料，壁面条件可看作是绝热壁。于是，本文选取了四个典型的壁温条件，包括一个绝热壁条件和三个等温壁条件(150 K，300 K，400 K)。不同壁温条件下，壁温与来流总温比如表2所示。

表2 不同壁温条件下壁温与来流总温比

3 计算结果分析

3.1 基本流分析

为便于比较，本文结果分析采用如下的无量纲化形式：

V*=V/V，T*=T/T

式中，Lx、Lz分别为钝三角翼外形的长度和底部半宽度，δ为当地边界层厚度，V∞为来流速度(860.838 m/s)，T0,∞为来流总温(420 K)。

图4为绝热壁条件下平板三角翼不同流向位置处的马赫数分布云图，由于工况为0°攻角状态，迎/背风流场对称，同一流向截面上从侧前缘至中心子午线发展，边界层逐渐增厚，并在中心区域形成流向涡结构。图5为三角翼表面压力系数及壁面极限流线分布，图6为无量纲最大横流速度分布，图中Z/Lz=0对应对称中心线位置，Z/Lz=1对应钝三角翼底部最大展向位置。可知除中心子午线流向涡区域和侧前缘区域外，翼身上壁面极限流线方向基本平行，无复杂流场结构。

图4 不同流向位置处的马赫数云分布

图5 表面压力系数分布及流线

由于中心对称线区域流动复杂，存在大尺度流向涡结构，流场变化剧烈，因此，后续采用线性稳定性理论分析时应避开该区域，且平板三角翼外形需考虑三维效应，故基于绝热壁状态流场，特别是中心流向涡尺度特征和边界层横流流动特征(如图6)，选择当地流线近乎平行、横流效应较弱位置Point1(x*=0.88，z*=0.2)，和靠近前缘、横流效应较强点Point2(x*=0.88，z*=0.8)两点进行研究，分析不同壁面温度条件对不同模态流动稳定性特征影响。

图6 横流速度分布

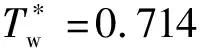
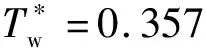
(a)Point1流向速度

3.2 稳定性分析

在获取各壁温条件基本流流场的基础上，针对平行性较好的流动区域(中心流向涡区域和侧前缘区域除外)开展了线性稳定性分析计算，获得了边界层流动的稳定性特征。

(a)Point1

图9、图10分别为不同壁面温度条件下Point1和Point2两点当地每个频率的最大增长率分布和中性曲线。图中，低频和高频两个分支分别对应第一模态和第二模态的扰动。ωr为扰动波的无量纲频率，βr为扰动波的展向波数。

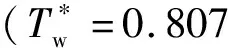
(a)Point1

(a)Point1

综上分析，可知：

2)由于钝三角翼存在复杂的三维边界层流动，不同展向位置的边界层稳定性特征不同，壁温的影响也出现差异，这与二维平板和0°攻角轴对称钝锥不同。Point2(靠近前缘区域)的横流模态扰动增长率与第二模态增长率幅值相当，且当地扰动增长率明显高于Point1(靠近对称中心线)，并先于Point1出现模态相交现象。

3.3 包络N值及转捩分析

四种壁温条件下整体包络N值在钝三角翼表面的分布情况见图12。

图13 转捩判据为Ntr=4.5时转捩线位置

为探讨转捩反转现象的内在机理，下面分析过Point1点最不稳定扰动波沿势流方向的变化情况。

首先提取不同壁温条件下Point1点处的包络N值及对应该包络N值的扰动波频率(本文称之为Point1点的最不稳定波频率)和扰动增长率，如表3所示。

表3 Point1点当地最不稳定扰动波参数

过Point1点对应最不稳定波频率的扰动波其增长率沿势流方向的分布如图14(a)所示，横轴ls*为无量纲势流方向距离。图14(b)、图14(c)分别为流向ls*≈0.0065位置(靠近扰动失稳起始点)和Point1点扰动增长率的频域分布，四个圆点分别为表3中提取的Point1点的最不稳定波频率对应增长率。

由图14(a)可知，对应Point1点最不稳定波频率的扰动增长率沿势流方向明显具有两个峰值，ls*=0.0065点和Point1点则分别位于前后这两个峰值区域内。

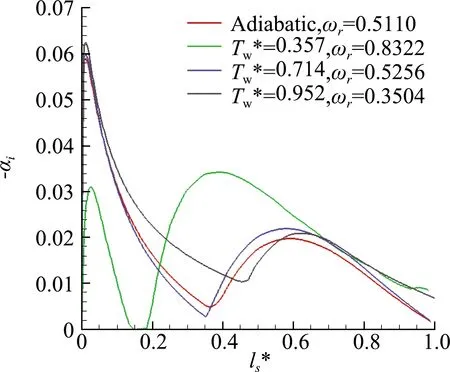
(a)增长率分布

图15 N值分布

由以上分析可知，转捩反转的内在机理在于大后掠角平板钝三角翼边界层流动独特的横流特征：在靠近前缘区域，横流效应强，扰动以横流模态和第一模态为主，形成一个扰动增长率峰值区域；而在靠近对称中心线的区域，横流效应弱，扰动以第二模态为主，形成另一个扰动增长率峰值区域。壁温比低于绝热壁值时，壁温比的增加主要影响第二个峰值区域，导致N值降低，转捩延迟；当壁温比超过绝热壁值后，壁温比对第一个峰值区域的影响超过了对第二个峰值区域的影响，导致N值增大，转捩前移。

4 结 论

本文研究了在地面风洞试验条件(M∞=6，Re∞=7.12×106/m，α=β=0°)下，壁面温度变化对大后掠角平板钝三角翼外形高超声速边界层流动稳定性及转捩的影响。所得结论如下：

2)壁温条件的变化对不同模态的扰动产生显著影响。壁温比升高促进横流模态和第一模态扰动增长，同时第二模态的扰动受到抑制。

3)随着壁温比的增加，受第一、第二模态联合作用影响，钝三角翼表面N值分布呈现先减小后增大的特点，预示存在转捩反转现象，反转点壁温比大约在绝热壁壁温比(约0.8)附近。

高超声速静风洞转捩试验中，来流总温低，壁温比的量值高(约0.7)，不少试验采用非金属模型，壁面可视为绝热壁。而在实际的高超声速飞行试验中，来流总温高，壁温比的量值低(量级大致在0.3)。本文的研究结果表明，这两种状态的稳定性特征差异大，这预示着可能存在显著的天地差异。显然，直接基于地面的静风洞试验结果来预示飞行条件下的转捩可能是不合适的，需要开展相关的天地差异分析和天地相关性研究。