两连发射弹出入水的轴对称超空泡流动特性

施红辉, 周东辉, 周 栋, 贾会霞

(浙江理工大学 机械与自动控制学院, 杭州 310018)

0 引 言

两连发射弹入水和出水问题，来源于从空中连续发射射弹灭雷、反潜火箭对同一位置的连续攻击、水下枪炮连续射击拦截或攻击低空飞行的目标等海战背景，在国防工业上有很高的应用价值。当射弹连续发射入水或出水时，需要评估多连发射弹的相互追尾以及超空泡流场之间的干扰，目前这些问题的详细研究还比较缺乏。由于连发射弹之间流场的相互影响，引起了复杂的水动力特性，进而影响了射弹的运动特性，使得它们的超空泡流动特性相比单发射弹有很大的区别并且更加复杂。因此，研究连发射弹出入水过程的超空泡流动特性十分重要。

目前，关于入水和出水问题的研究，国内外已经有了许多研究成果，但它们主要是针对孤立的单个物体或射弹的。针对入水问题，Vlasenko[1]介绍了用蒸汽弹射器将速度为90 m/s的射弹垂直向下入水的实验，他还首次研究了水箱尺寸对超空泡形状的影响。Truscott等[2]利用高速摄像技术研究了弹体以小攻角入水时弹体表面诱导产生的超空泡流动态特性，并讨论了长径比与弹体头型对入水时产生超空泡的形态影响。Weiland和Vlachos[3]通过实验研究了圆柱形射弹高速入水空泡的产生和发展，并指出射弹发射时驱动气体的泄露促进了超空泡的快速形成。Lee等[4]利用能量守恒原理对射弹高速入水空泡生成、发展过程及闭合特性进行了研究，建立了高速入水条件下的入水空泡动力学模型。Panahi[5]基于有限体积法利用动网格技术模拟了楔形体入水和圆柱体出水问题。Nair等[6]利用CFD方法对球形及两种锥角的轴对称物体进行了三维入水数值模拟，分析了物体入水时自由面的变化、物体的运动特性以及轨迹的偏移等。在国内，王焕然等[7]对入水超空泡的形状进行了实验观察以及理论建模计算，他们的理论模型借鉴了Lee等[4]推荐的空泡能量平衡理论。徐胜利等[8-9]对入水速度超过1 km/s的超空泡流场进行了实验和SPH数值模拟研究。郭子涛和张伟等[10-11]对几种柱形弹体入水进行了实验和理论研究，建立了关于空泡扩展的理论模型。马庆鹏等[12-13]采用VOF多相流模型，利用动网格技术对锥头圆柱体垂直自由高速入水问题开展了数值模拟研究，得到了入水空泡演化过程以及深闭合过程空泡流场的流动特性和压力分布特性。魏英杰等[14]采用实验和数值模拟相结合的方法研究了超弹性球体垂直入水的空泡流动，发现了超弹性球体入水特有的球体变形行为和空泡形态。蒋云华等[15]对约束姿态弹丸在不同的入水角度和通气量下进行了入水实验。孙亚亚等[16]利用Flunet软件，采用VOF多相流模型对带有不同凹槽数空化器的航行体诱导的超空泡进行了数值模拟，发现数值计算结果与Logvinovich半经验公式计算结果具有较好的一致性。鲁林旺等[17]利用Flunet软件对水下带有不同尾翼数高速射弹的超空泡流特性进行了数值模拟,分析了尾翼数的不同对超空泡形成和发展的影响，以及不同尾翼数下射弹的阻力系数。针对出水问题，Xing-Kaeding等[18]对航行体的出水过程中自由液面和空泡溃灭现象进行了研究，得到航行体在恒定的速度出水过程中自由液面和空泡的溃灭以及重力出水弹道的影响规律。Liju等[19]对轴对称体垂直出水时产生的浪涌影响进行了实验研究，利用高速摄影仪拍摄到了圆柱体刺破自由面时的浪涌轮廓。鲁传敬等[20]在考虑黏性和重力的情况下，利用CFD方法以及动网格技术模拟了燃气流场、水场和弹丸运动轨迹的耦合流场。魏海鹏等[21-22]通过求解N-S方程数值分析了出水物体表面上的压力系数，考虑了肩空泡(局部超空泡)溃灭时产生的冲击力的贡献。王一伟和黄晨光等[23-24]对典型航行体模型水下发射的全过程进行数值模拟，得到了航行体周围空泡演化过程、表面压力分布变化、航行体关键截面的全时程载荷响应。颜开等[25-27]对出水空泡的行为进行了实验观察和数值计算，发现空泡前端的拍打和后端的闭合，造成了高压的出现。卢佳兴等[28]基于高速摄像技术研究了两发回转体齐射出水过程中的空泡演化特性和运动特性。

施红辉等[29]曾对两连发和三连发射弹以100 m/s的速度在水下水平匀速运动诱导的超空泡流场进行了数值模拟。但是，对于连发射弹入水的研究，目前公开的文献还很少。只有何春涛等[30]对在重力加速下低速两射弹串联倾斜入水问题进行了初步实验，发现当两射弹串联间距较小时，后发射弹完全进入到前发射弹形成的空泡内部。而对于连发航行体出水的研究还未见公开报道过。

本文针对两连发射弹垂直入水和出水问题，基于N-S方程的有限体积法，引入VOF多相流模型和Schnerr-Sauer空化模型，分别建立了两连发射弹入水和出水的二维轴对称数值模型，以FLUNET流体仿真软件为平台，利用动网格技术研究了两连发射弹入水和出水过程中的超空泡演化特性及流体动力学特性。研究结果揭示了两连发射弹入水和出水过程中诱导的超空泡流动的典型特征及相关力学参数。

1 控制方程及数值方法

1.1 控制方程

数值计算采用流体体积函数(VOF)多相流模型描述水、水蒸气、空气构成的多相流动系统。VOF多相流模型将水、水蒸气、空气三相当做单一介质的混合流动系统，各相共享一套动量方程，通过计算得到单元内各相的体积分数确定流动系统中各相的分布。

混合相的连续方程和动量方程分别为：

(1)

(2)

式中：t为时间；ui、uj分别为笛卡尔坐标系中的速度分量；ρm为混合相密度；P为流场的压力；μm为混合相动力黏度；SM为附加的源相。

ρm、μm的表达式分别为：

ρm=αvρv+αgρg+αlρl

(3)

μm=αvμv+αgμg+αlμl

(4)

式中：αv、αg、αl分别为水蒸气相、空气相、水相的体积分数；ρv、ρg、ρl分别为水蒸气、空气、水的密度；μv、μg、μ1分别为水蒸气、空气、水的动力黏度。

数值计算采用RNGk-ε湍流模型[31]，由于空化现象是流线强烈弯曲导致的，该模型能够更好地处理高弯曲流线和及高应变率的流动。湍动能k和耗散率ε的控制方程分别为：

(5)

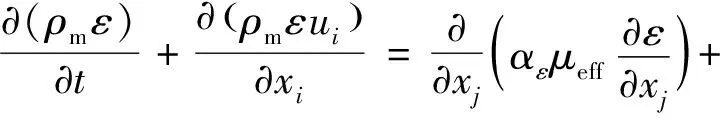
(6)

式中：μeff=μm+μt，μt为湍流黏度；k为湍动能，ε为耗散率；αk、αε分别为k和ε的负向效应的普朗特数；Gk为平均速度梯度产生的湍动能；C1ε、C2ε为湍流动能耗散率的经验常数。

1.2 空化模型

空化模型选择Schnerr-Sauer空化模型[32]，该空化模型具有较高收敛速度和计算稳定性。水蒸气相方程的一般形式为：

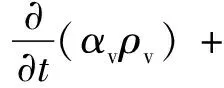
(7)

(8)

(9)

式中：vv为水蒸气相的速度矢量；Re、Rc分别为蒸发速率和冷凝速率；RB为气核的半径；Pv为水的饱和蒸汽压力。

1.3 数值方法和边界条件

两连发射弹的计算模型为轴向串联的两发射弹，定义前发射弹尾部和后发射弹头部的距离为两射弹的间距ΔH，两发射弹的物理尺寸和质量完全相同，射弹的物理模型为直径D=6 mm、长度L=48 mm的圆柱体，长径比为8，如图1所示，质量为3.56 g。由于射弹模型为轴对称回转体，数值计算采用二维轴对称模型。整个网格区域宽度是60D，长度是160D，足够避免边界效应。数值模拟中采用射弹运动、流体静止的方法研究连发射弹的入水和出水，这种方法更接近真实的环境。两连发射弹垂直入水和出水的计算域如图2所示，图2(a)表示两连发射弹垂直入水的计算域，图2(b)表示两连发射弹垂直出水的计算域。这两种计算域边界条件划分相同，上边界条件为压力出口边界条件，下边界条件为压力入口边界条件，左侧边界条件为无滑移壁面条件，射弹设置为无滑移壁面条件。整个计算域采用四边形结构网格划分，射弹附近的网格进行局部加密处理。通过用户自定义函数(UDF)编写程序嵌入到FLUNET软件中实现两连发射弹的垂直自由运动，在运动过程中网格的更新和生成采用动网格技术中的动态层法实现。

图1 射弹的物理模型

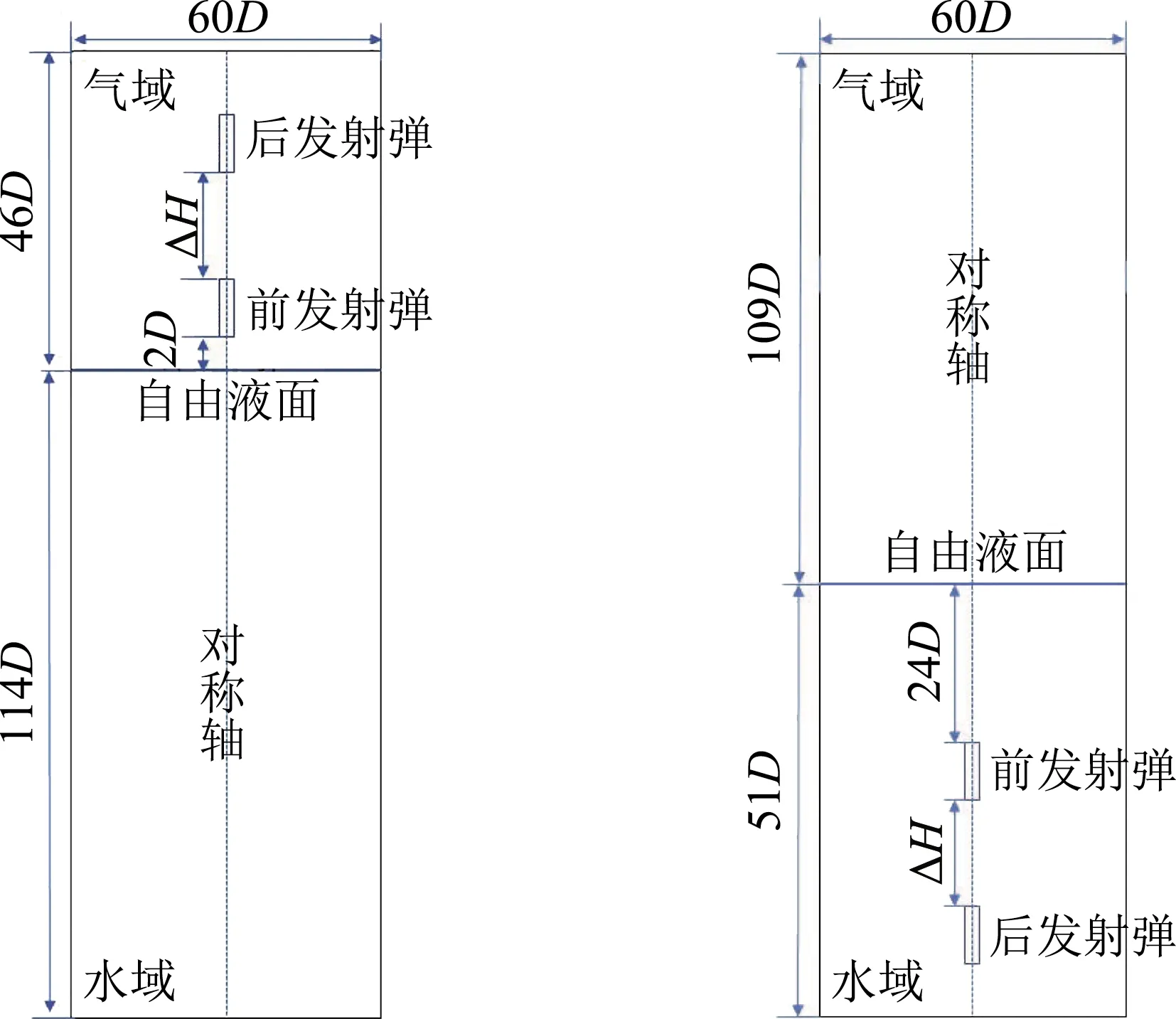
(a)两连发射弹垂直入水的计算域 (b)两连发射弹垂直出水的计算域

对于上述计算模型压力与速度之间的耦合求解采用 PISO算法，压力场的空间离散采用PRESTO!格式，各项体积率离散采用CICSAM格式，密度和动量采用二阶迎风离散格式，空间离散采用二阶迎风格式，时间离散采用一阶隐格式。

2 数值方法验证

首先进行了网格无关性验证，对自由面和射弹周围进行了网格加密，建立了3种不同网格密度的网格，网格数分别为56.34万(Case1)、68.51万(Case2)、82.67万(Case3)，分别对发射速度为100 m/s的两连发射弹入水进行了数值模拟，得到了前发射弹运动速度随时间的变化曲线，如图3所示。从图中可知，随着网格密度的增加，Case2的网格密度和Case3的网格密度计算所得的前发射弹运动速度之间的差异已经非常小了，综合考虑计算精度和时间成本，选取了网格密度为Case2的网格用于本文计算。

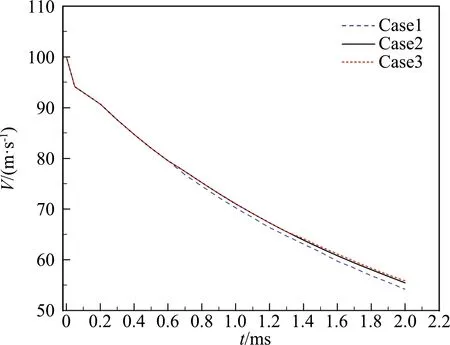
图3 不同网格密度的计算结果

关于连发射弹高速入水或出水的研究缺乏相关的文献报道，并且实验难度很大，所以采用上文所述的计算方法和边界条件分别对文献[11]中的单发平头圆柱体入水实验和文献[33]中的工况10的单发射弹出水实验进行了数值模拟。数值计算中入水运动参数设置与实验一致，该平头圆柱体直径为12.65 mm，长25.4 mm，质量为22.52 g，入水初速度为142.7m/s。将数值模拟得到的速度和入水浸彻位移随时间的变化分别与实验结果进行对比，结果如图4和图5所示，从图中可以看出，数值模拟结果与实验结果具有较高的一致性。图6比较了数值模拟和实验在t=3 ms时获得的入水空泡形状，两者的空泡形状基本一致。对文献[33]中射弹出水实验的工况10进行了数值计算，实验采用的射弹头形为圆台形，头部直径为3 mm，长度为48 mm，质量为2.983 g，水深为480 mm，出水初速度为83.28 m/s。图7给出了实验和数值模拟关于射弹出水时空泡的演化过程，图中每相邻两张图片的时间间隔 Δt=0.25 ms，从图中可以看出数值模拟结果和实验结果对应良好。已证明该数值方法计算出的空泡轮廓与Logvinovich的理论计算结果一致[16-17]。验证有效地证实了数值模拟方法的准确性。

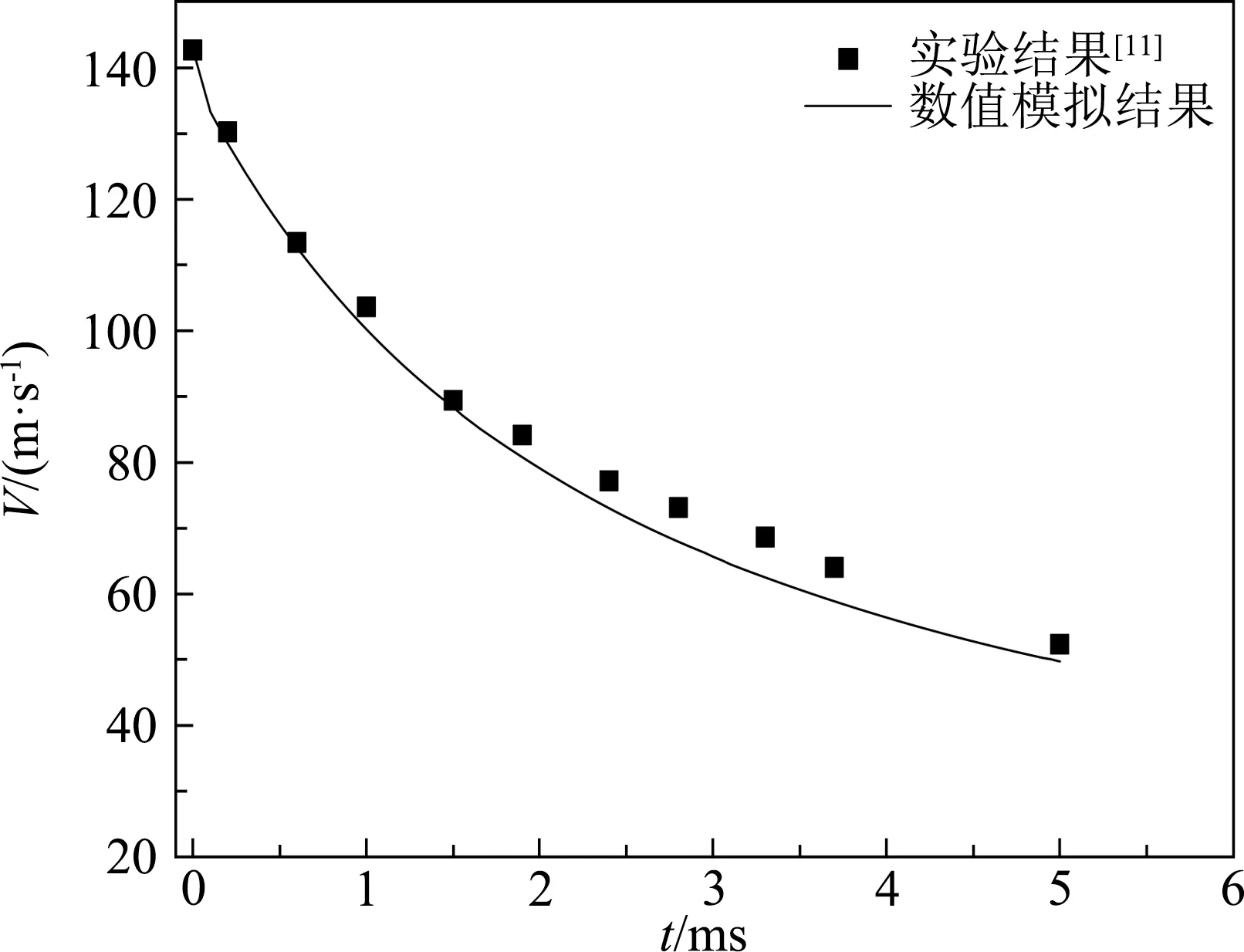
图4 射弹入水速度衰减的数值模拟和实验结果[11]对比

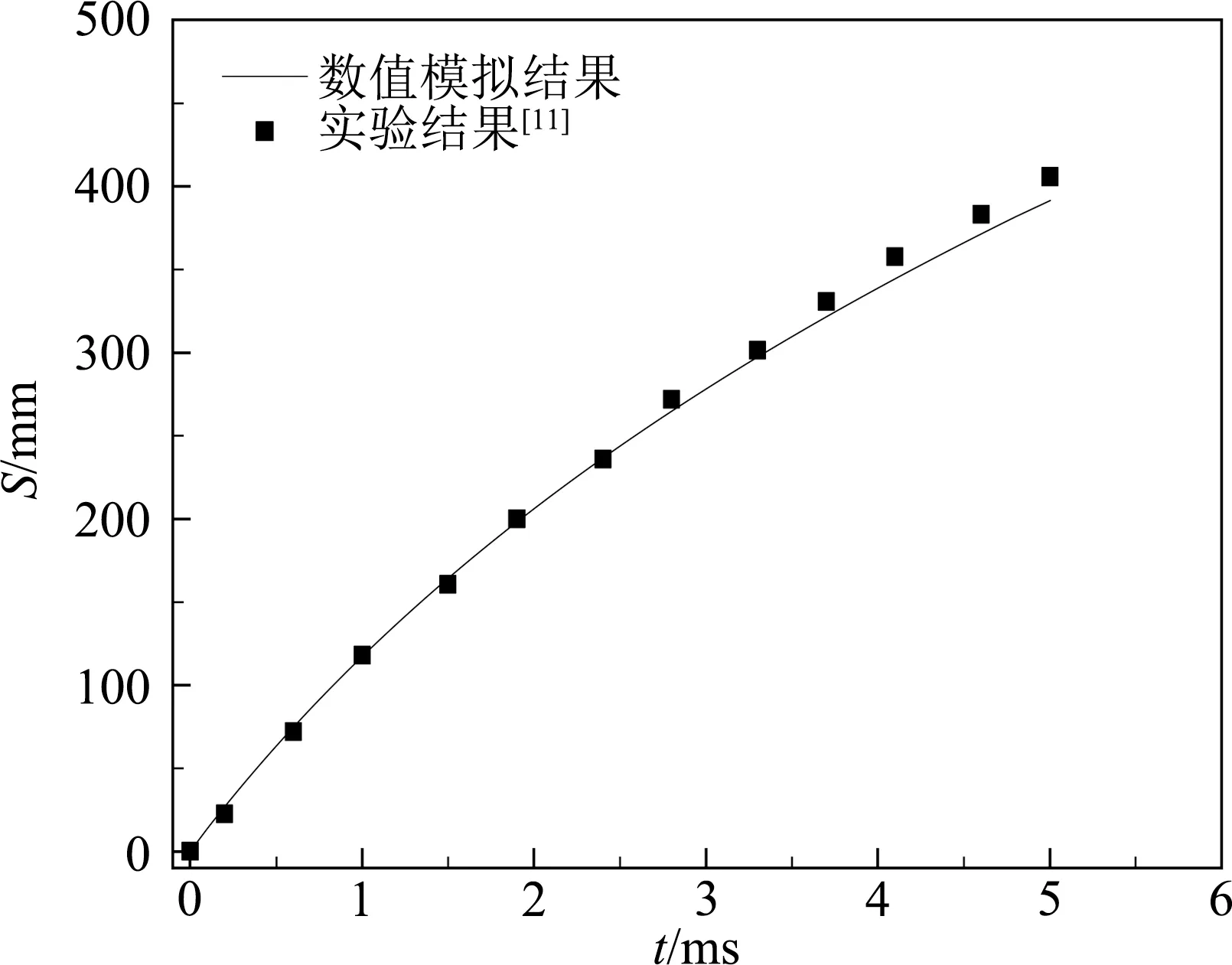
图5 射弹入水浸彻位移的数值模拟和实验结果[11]对比

图6 数值模拟和实验[11]在t=3 ms时的入水空泡形状

(a)实验结果

3 结果与讨论

3.1 两连发射弹入水分析

取前发射弹头部与自由液面刚接触的时刻为时间零点,当初速度V0为100 m/s，两射弹的间距ΔH=10D时，两连发射弹的入水空泡形态随时间的变化如图8所示，图中红色代表水相，蓝色代表水蒸气相和空气相。从图中可以看出，前发射弹先经历了入水撞击、开空泡、空泡表面闭合。在空泡表面闭合阶段出现了圆拱状的水幕闭合且伴随着产生了一股向上的射流和一股向下的射流，表面闭合后形成了一个封闭的超空泡。随着前发射弹的运动，封闭的超空泡被向下运动的射弹拉离液面，并且向下的射流变粗。后发射弹在接近自由液面时与前发射弹面闭合时形成的向上射流相遇，迎着射流后发射弹撞击自由液面并形成一个很小的开口空泡。随着后发射弹的运动，引起开口空泡和前发射弹的超空泡融合，融合后前发射弹的超空泡由闭合空泡重新变成了开口空泡。在液体张力和压差等的作用下，融合后的开口空泡在近自由液面附近再次发生闭合，闭合后产生了垂直向上的射流。在t=2.3 ms时，后发射弹追上前发射弹并发生追尾碰撞，碰撞后两者共同运动。此处只考虑了两发射弹碰撞后一起运动的情况，没有考虑两发射弹碰撞后分离的情况，两射弹碰撞后发生分离的情况涉及更复杂的力学机制，还需要进一步研究。在两射弹发生撞击时，超空泡壁面上出现了一个波动现象，表现为前发射弹头部流动分离点附近的空泡壁面出现波谷，此后该波动现象一直存在。数值计算发现存在波动的空泡壁面易发生崩溃，可推测此现象产生的原因是由两射弹碰撞产生的瞬态扰动引起。随着时间的推移，空泡从它的尾部位置逐渐溃灭。

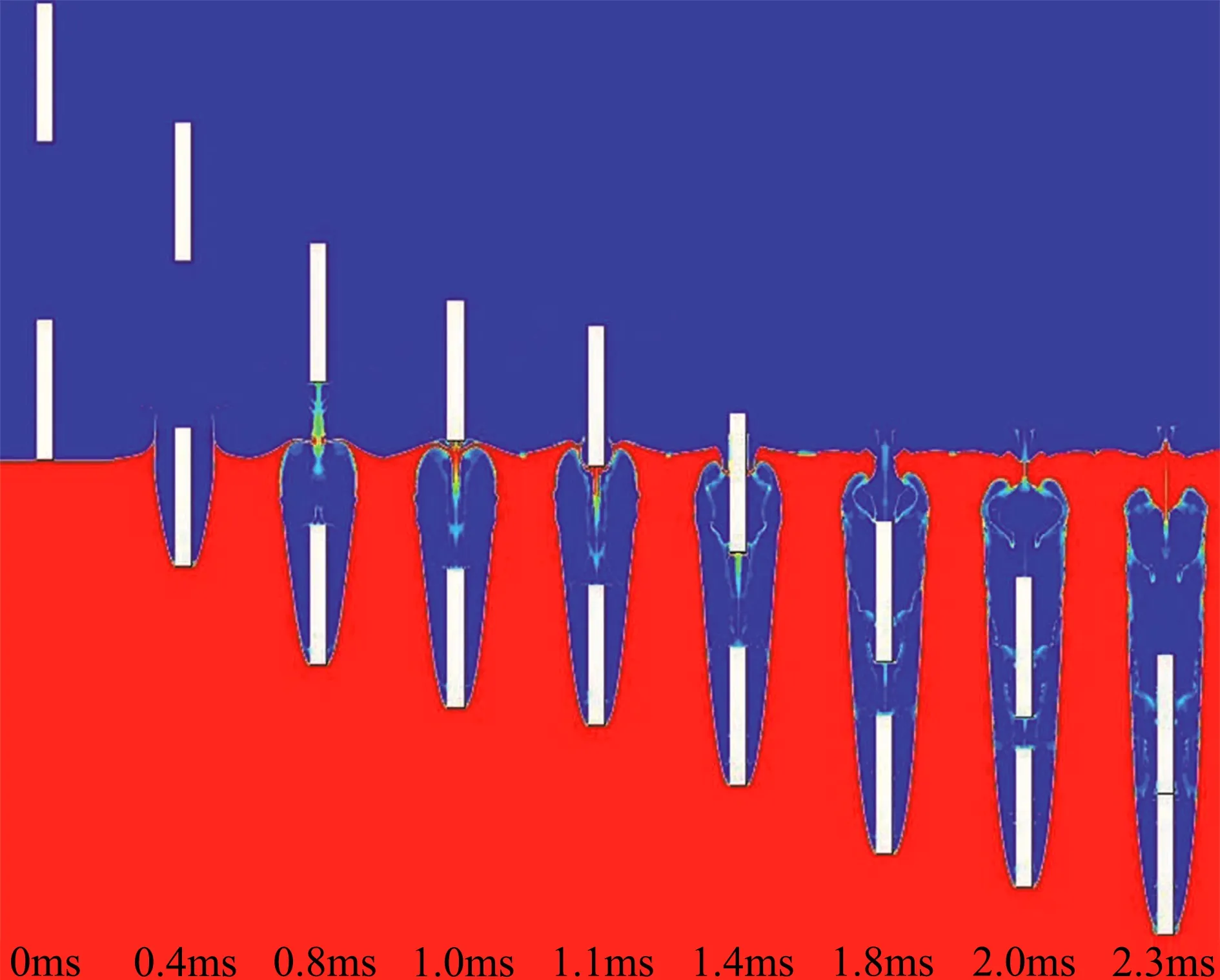
(a)两射弹追尾前，入水空泡的演化

图9表示两连发射弹入水空泡的气相图(红色为空气相，蓝色为水相，绿色为水蒸气相)。从图中可以看出入水空泡内有空气相和水蒸气相。前发射弹开空泡阶段，空气首先连续从大气进入空泡中，空气的卷入开始是由于射弹诱导的气流，随后空气被空泡的负压吸入空泡，空泡内的气体绝大部分是空气。由于射弹的高速运动，流动分离点附近产生低压区，水在此处首先发生相变产生水蒸气，水蒸气主要分布在空泡壁面附近。在t=0.8 ms时，空泡发生了表面闭合，进入空泡的空气流就终止了，空泡的尾部产生了再进入射流，由于存在的低压使液体射流发生相变转化为水蒸气，因此空泡尾部存在大量的水蒸气。由于水面下存在前发射弹的超空泡流场，后发射弹形成的开口空泡尺寸很小。前发射弹的空泡和后发射弹的空泡随后发生融合，融合后的空泡再次成为开口空泡，此时大气中的空气再次被吸入空泡内；之后空泡再次发生闭合，空泡中的蒸汽相越来越多。

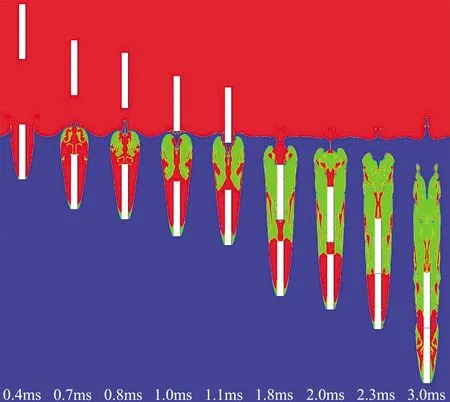
图9 两连发射弹入水空泡的气相图

图10所示为两连发射弹在发生追尾前各自头部中心点压力随时间的变化关系，纵坐标表示无量纲压力P/P0。从图中可以发现，前发射弹在入水撞击阶段受到巨大的入水砰击压力，压力在极短的时间达到峰值，约为49，随后逐渐下降。后发射弹头部中心点所受压力开始阶段平缓变化，这是由于后发射弹此时间段还在空气中运动，没有入水，此时后发射弹头部中心点所受的压力很小；随后后发射弹头部中心点压力曲线出现两个峰值，第1个压力峰值约为51个标准大气压，第2个压力峰值为39个标准大气压，出现第2个压力峰值后压力急剧下降，最后趋于稳定。第一个压力峰值的出现是由于后发射弹与前发射弹空泡发生面闭合时形成的垂直向上的射流相遇导致的，第二个压力峰值是后发射弹头部发生撞水导致的。对比前发射弹和后发射弹，在撞水时刻，后发射弹头部中心点所受的压力小于前发射弹的，这是因为后发射弹受到前发射弹入水形成的空泡流场的影响。在两发射弹各自入水后，后发射弹头部中心点压力相比前发射弹下降得更快并且压力值更小，这是由于入水后，后发射弹很快进入到前发射弹的空泡内部，空泡内的水蒸气密度远小于水的密度。

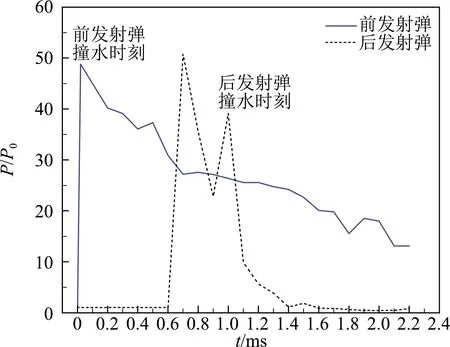
图10 两连发射弹发生追尾前其头部中心点压力随时间的变化

图11是前发射弹入水后0.1 ms和1.1 ms时的压力云图。从图中可以看出，前发射弹和后发射弹分别在入水后，前发射弹头部的压力值和高压区范围都远大于后发射弹的，这主要是由于后发射弹受到了前方空泡流场的影响。在后发射弹入水阶段，前发射弹已经形成了表面闭合的空泡，后发射弹撞水实际撞击的是前发射弹诱导的闭合拱状水幕，由于水幕很薄，并且水幕下方还存在低压的空泡流场。

(a)t=0.1 ms

图12给出了两连发射弹速度随时间变化的曲线。从图中可以看出前发射弹入水后速度衰减很快，这表明航行体在入水初期受到的阻力非常大。后发射弹入水后速度有一定程度的衰减，随后速度变化不明显，这是由于后发射弹进入到前发射弹形成的超空泡中，其受到的阻力比在水中的阻力小得多。在时间t=2.3 ms，两射弹的速度发生跃变，前发射弹的速度变大，后发射弹的速度变小，这是由于前发射弹和后发射弹发生追尾碰撞。碰撞后，两发射弹以相同的减速度衰减。

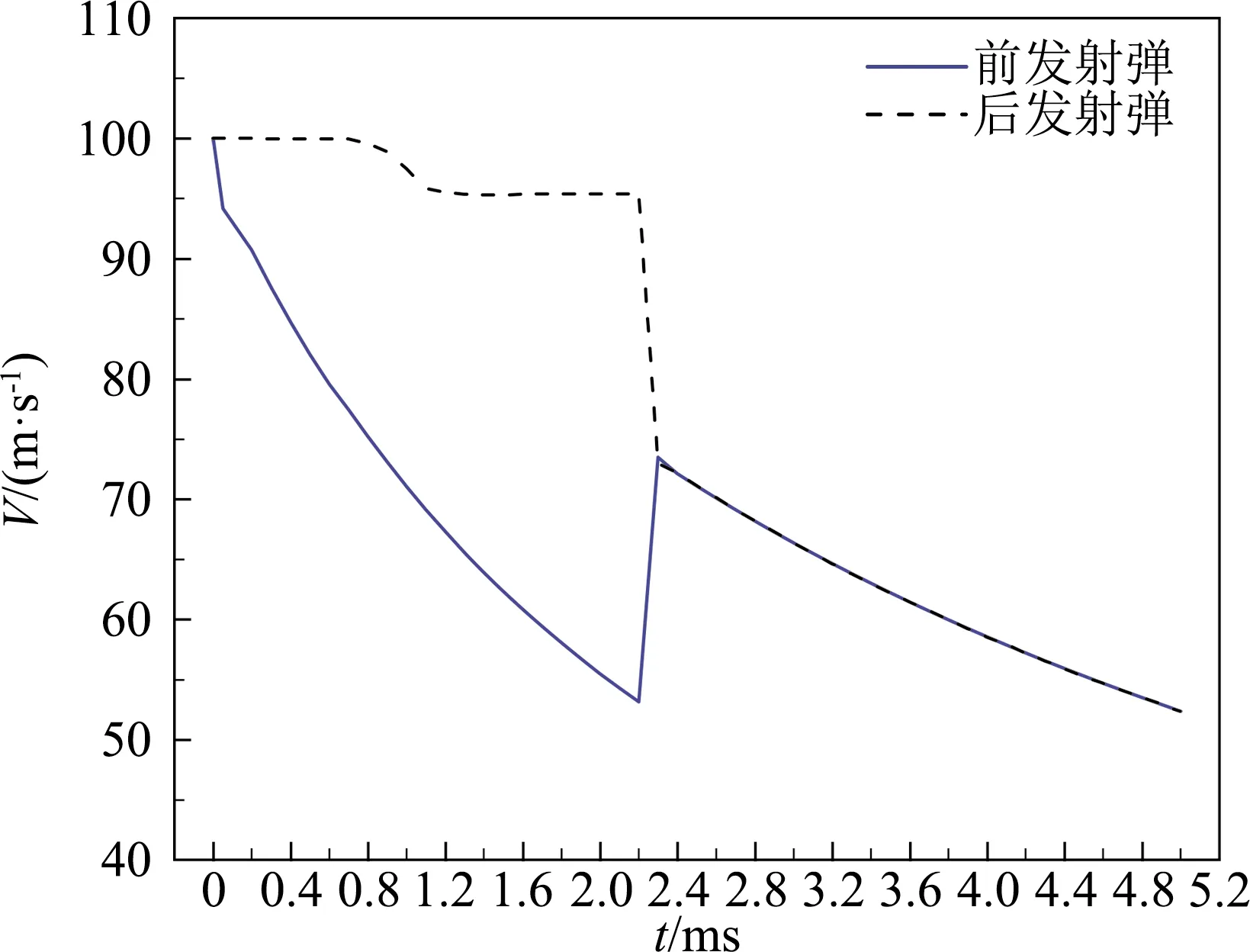
图12 两连发射弹速度衰减曲线

图13是两连发射弹位移随时间变化的曲线，其中纵坐标为无量纲位移Y/D，位移的坐标原点在自由液面上，正方向沿水深竖直向下。从图中可以看出随着时间的增加，两射弹之间的距离越来越小，在t=2.3 ms，前发射弹和后发射弹正好相距1个射弹的长度(48 mm)，说明此时后发射弹追上前发射弹。

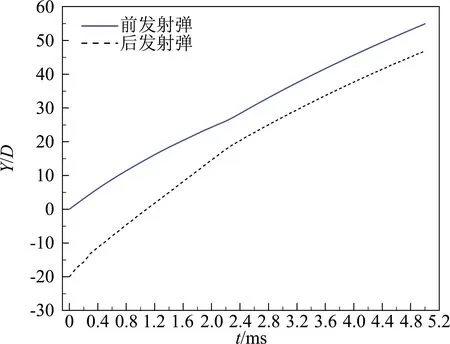
图13 两连发射弹位移随时间变化曲线

3.2 两连发射弹出水分析

对于两连发射弹的出水研究，出水过程忽略横流和侧风的影响，只考虑理想情况。初速度V0为100 m/s、ΔH=20D时，两连发射弹的出水超空泡形态随时间的变化如图14所示，图中红色代表水相，蓝色代表水蒸气相和空气相，时间零点取前发射弹头部刚接触自由液面的时刻。射弹在水中垂直向上运动，由于射弹的运动速度较高，前发射弹和后发射弹分别独立形成自然超空泡，前发射弹在接近自由液面时，在射弹向上运动和液体黏性力等作用下，此时水面发生抬升和隆起，并形成包裹空泡的水膜。t=0.5 ms时前发射弹伸出水面并带出水冢，前发射弹诱导的空泡直到前发射弹完全出水后才开始溃灭，当前发射弹尾部离开水面时托出了一个水柱。前发射弹由于出水速度比较高，它诱导的超空泡来不及随射弹出水而被剥离在水面下，接着后发射弹运动过来，此超空泡在环境压力与空泡内部压力的巨大压差作用下以及后发射弹的冲击下从头部和尾部迅速收缩溃灭。后发射弹的头部和肩部进入前一个超空泡内时，后发射弹逐渐剥离自身的超空泡，剥离后的超空泡在压差的作用下也逐渐溃灭。前发射弹留下的超空泡溃灭后，后发射弹的头部重新与水接触，产生了新的空泡，由于此时后发射弹的速度已较低，新产生的空泡已不能覆盖整个射弹，即形成局部超空泡。后发射弹在穿越水面阶段，其形成的局部空泡发生溃灭，后发射弹的尾部离开水面时同样拖出了水柱。

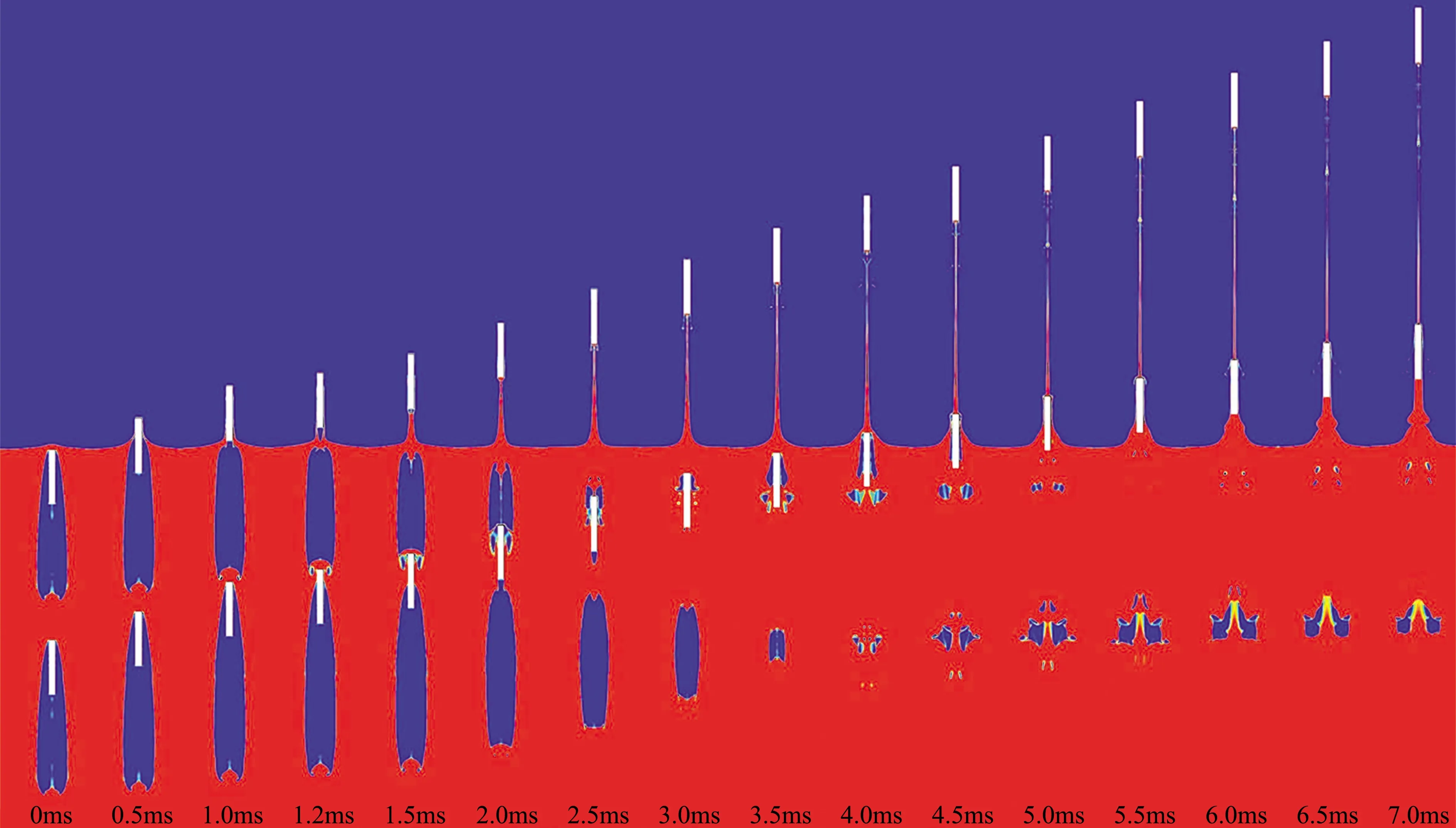
图14 两连发射弹出水超空泡演化过程

图15是两连发射弹出水过程中特定时刻的压力云图。前发射弹在穿越自由液面的过程中，闭合的超空泡壁面开始与大气相连打开，空泡内压立即由水的饱和蒸汽压(3540 Pa)逐渐增加为一个大气压，空泡内压力增大从空泡头部逐步向尾部扩散，从而促使了超空泡的快速溃灭。后发射弹在接近前发射弹超空泡尾部过程中,它前方的压力值逐渐降低，并且高压区范围缩小，当后发射弹头部进入前一个空泡内部时，它头部前方的高压区消失，引起压差阻力大大减小，因此当后发弹出水时，前发射弹形成的超空泡有利于后发射弹减少水的阻力。

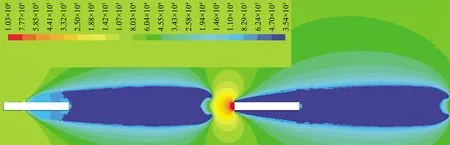
(a)t=0.5 ms

图16给出了两连发射弹出水前后速度的变化。在出水前，两发射弹的速度衰减趋势相同。前发射弹出水后进入了空气中，其受到的阻力很小，速度衰减不明显。后发射弹在出水前遇到了前发射弹剥落的超空泡，导致其所受的阻力很小，引起后发射弹速度基本不变。当前发射弹的超空泡溃灭后，t=2.6 ms时，后发射弹的速度急剧地衰减。从5 ms至7 ms，后发射弹的速度仍在持续较少，是因为较粗的水柱对射弹的拖拽导致的(见图14)。

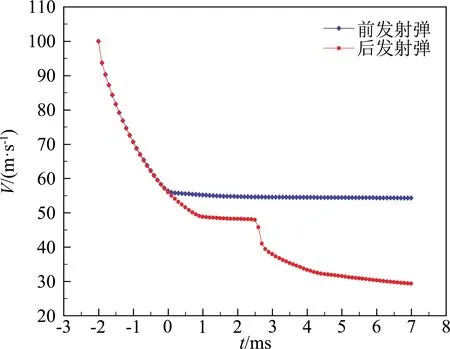
图16 两连发射弹出水速度衰减曲线

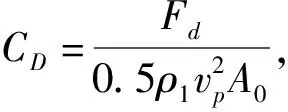
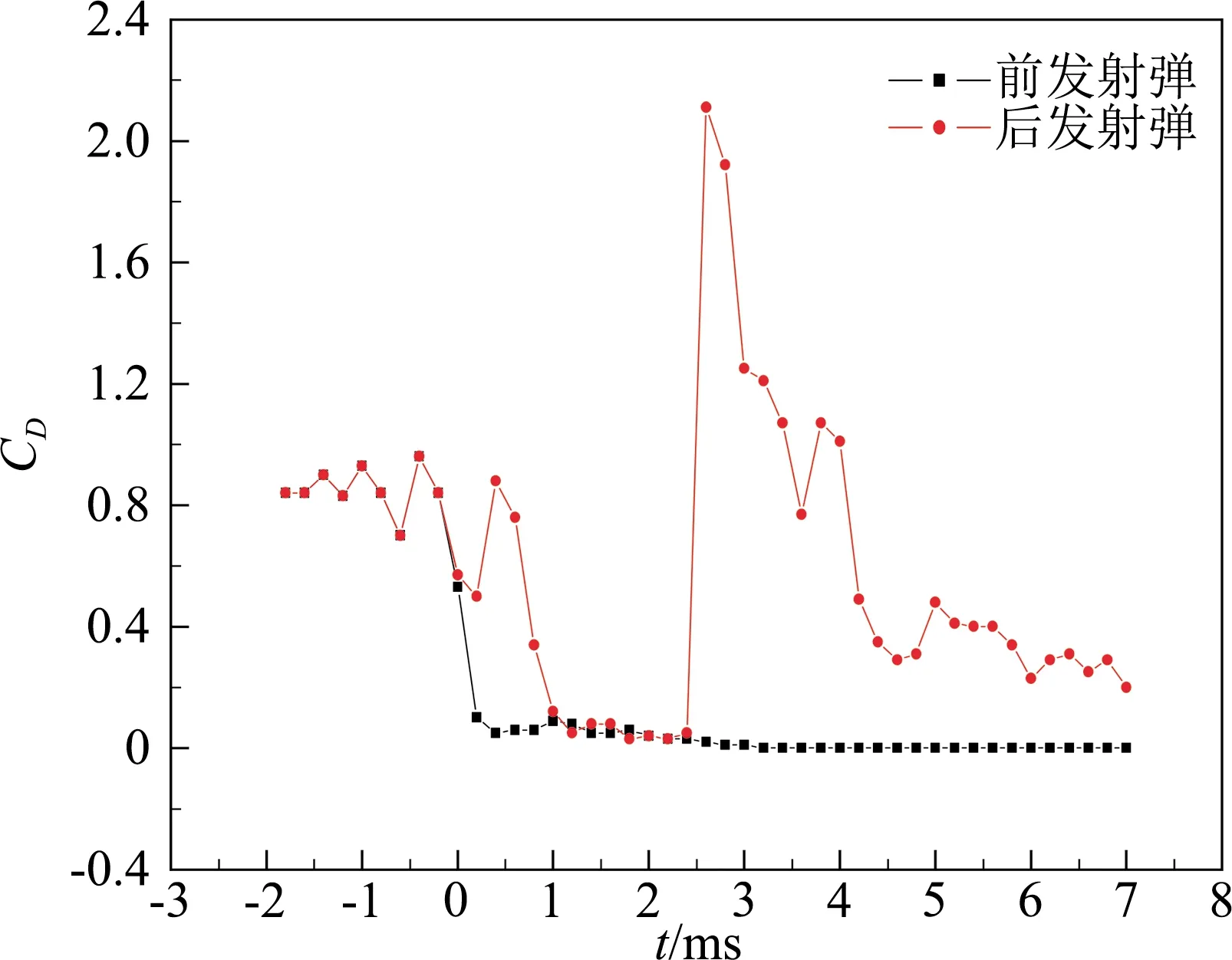
图17 两连发射弹出水过程的阻力系数随时间变化

4 结 论

本文以两连发射弹出入水过程的超空泡流场为研究对象，开展了两连发射弹在发射速度V0为100 m/s的出入水数值模拟，揭示了一些新的流体力学现象，将能为分析更复杂工况下的流场提供必要的支撑，也可为相关工程设计提供一定的参考。主要结论如下：

1)对于两连发射弹入水，前发射弹形成的超空泡流场对后发射弹的空泡发展造成影响，后发射弹形成的开空泡尺寸远小于前发射弹的，前、后发射弹各自诱导的空泡能够相互融合成1个空泡，导致后发射弹进入了前发射弹的超空泡内部运动。两发射弹的追尾碰撞在超空泡的壁面上引起了扰动，并且空泡易在有扰动的位置发生崩溃。后发射弹头部中心点压力出现了两个峰值，分别为后发射弹头部受到前发射弹空泡面闭合形成的向上射流的冲击、后发射弹入水撞击阶段受到的冲击，另外后发射弹入水撞击阶段受到的冲击载荷远小于前发射弹的。后发射弹进入到前发射弹的超空泡中时，其所受阻力很小，速度几乎不再衰减，而前发射弹继续受到水的阻力作用，速度继续衰减，导致后发射弹逐渐追赶上前发射弹并发生追尾碰撞。

2)对于两连发射弹出水，前发射弹基本不受后发射弹影响，与单发射弹出水过程类似，而后发射弹受前发射弹超空泡流场的干扰，后发射弹发生脱离自身超空泡、进入前发射弹超空泡、超空泡溃灭、生成新的局部超空泡等行为，在干扰过程中，后发射弹的阻力系数先较小后增大，出现了一个峰值，其速度先基本保持不变再到急剧的衰减，这与单发超空泡射弹出水有很大的区别。