超声速边界层中的模态转换及壁温影响效应

苏彩虹, 宋明真

(天津大学 机械学院 高速空气动力学研究室, 天津 300072)

0 引 言

边界层转捩预测是飞行器设计中的重要问题，因为湍流状态下壁面摩阻比层流下大得多，而高速飞行时，湍流状态下的壁面热流也比层流大好几倍。因此，只有准确预测转捩位置，才能合理预估摩阻和表面热流[1-3]。从小扰动开始的自然转捩具有以下几个典型的特征阶段：1)感受性，即自由流扰动通过一定机制转换为边界层内不稳定波的过程；2)边界层内不稳定波的线性增长；3)幅值增长到一定程度的非线性作用及转捩至湍流。因此，想要从理论的角度做完全基于物理机制的转捩预测，必须要回答以下三个问题[4]：1)自由流扰动如何激发边界层内不稳定波；2)边界层内的不稳定波如何演化；3)不稳定波发展到何种程度转捩便会发生。

目前为止，以上问题中，只有第二个问题的线性演化阶段有成熟的理论进行描述，即线性稳定性理论。线性稳定性理论基于局部平行性假设[5]，给定来流条件和扰动，求解Orr-Sommerfeld方程的特征值问题，可以计算边界层内不稳定模态的增长过程。目前，基于线性稳定性理论的eN方法被认为是最有理论依据的转捩预测方法，已在低速流的转捩预测中取得了丰硕成果。然而，对于高速流的转捩预测，远没有低速流的成功。主要有两方面的原因：一是，在高速流中用以确定转捩判据N值的实验和经验远没有低速流中的多；二是，在高速流中感受性的机制与低速流中显著不同，导致eN方法所隐含的感受性的考虑，即所有扰动波在中性点处都具有相同的初始幅值，不再成立。Su & Zhou曾在对小攻角高超声速圆锥进行转捩预测时，对eN方法提出过两个改进意见[6]，改进后的eN方法证实可以得到与实验相比更合理的结果[7-8]。

不少研究表明，正确考虑感受性机制成为高速边界层转捩预测成功的关键[9]。与不可压边界层中的“尺度转换”机制不同[10-12]，高速边界层中不稳定波的激发是通过“同步”或“共振”机制实现的[13-18]。同步是指，频率相同的自由流扰动与边界层模态具有相同或相近的相速度，后者就会由前者激发。高超声速圆锥边界层的感受性研究表明[19]，自由流中的快、慢声波会分别激发边界层内的快、慢模态。在向下游的演化过程中，快模态的相速度逐渐减小，慢模态的相速度逐渐增大，直到与第二模态波相同(或相近)，从而将后者激发。由于高空中不存在声源，因而并不存在声波，主要的扰动源可能是由湍流脉动及密度或温度不均引起的涡波和熵波。数值研究表明[20-21]，涡波和熵波可以通过与头部激波作用，产生激波后的声波，激波后的声波再通过同步机制激发出快模态，快模态向下游演化，通过模态转换激发不稳定的第二模态。

对于马赫数大于4的超声速边界层，Mack第二模态是边界层中起主导作用的不稳定模态。Fedorov[13]曾采用多尺度法研究了快模态到第二模态的转换机制，表明在模态转换区域附近，非平行性扮演着非常重要的作用。因此，基于局部平行假设的线性稳定性理论无法描述快模态到第二模态的转换过程。若能发展从快模态出发、考虑模态转换的转捩预测方法将比原有的半经验方法更有物理依据。

本文以超声速平板边界层为研究对象，采用数值方法研究了快模态与第二模态间的模态转换过程，构建了模态转换系数和模态转换区域与扰动频率之间的模型公式。基于此，发展了从快模态出发、考虑模态转换的扰动幅值的计算方法。该方法可以准确描述多个壁面温度条件下包含模态转换过程的扰动演化。

1 计算参数和数值方法

1.1 计算工况

1.2 直接数值模拟方法

本文分别采用直接数值模拟方法(DNS)和线性抛物化稳定性方程(PSE)的方法计算快模态向下游的演化。

DNS采用的是二维N-S方程的扰动形式，即:

(1)

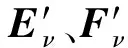
(2)

其中，C0=110.4 K。

采用有限差分方法离散控制方程。对流项采用五阶迎风差分格式，黏性项采用六阶中心差分格式，时间推进采用四阶Runge-Kutta格式。壁面分别采用无滑移和等温壁面边界条件，上边界为无反射特征边界条件。计算域入口的扰动由线性稳定性理论(LST)分析给出，即:

(3)

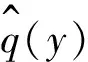
1.3 抛物化稳定性方程

线性的抛物化稳定性方程(PSE)具有如下形式：

(4)

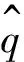
2 超声速边界层中的模态转换过程

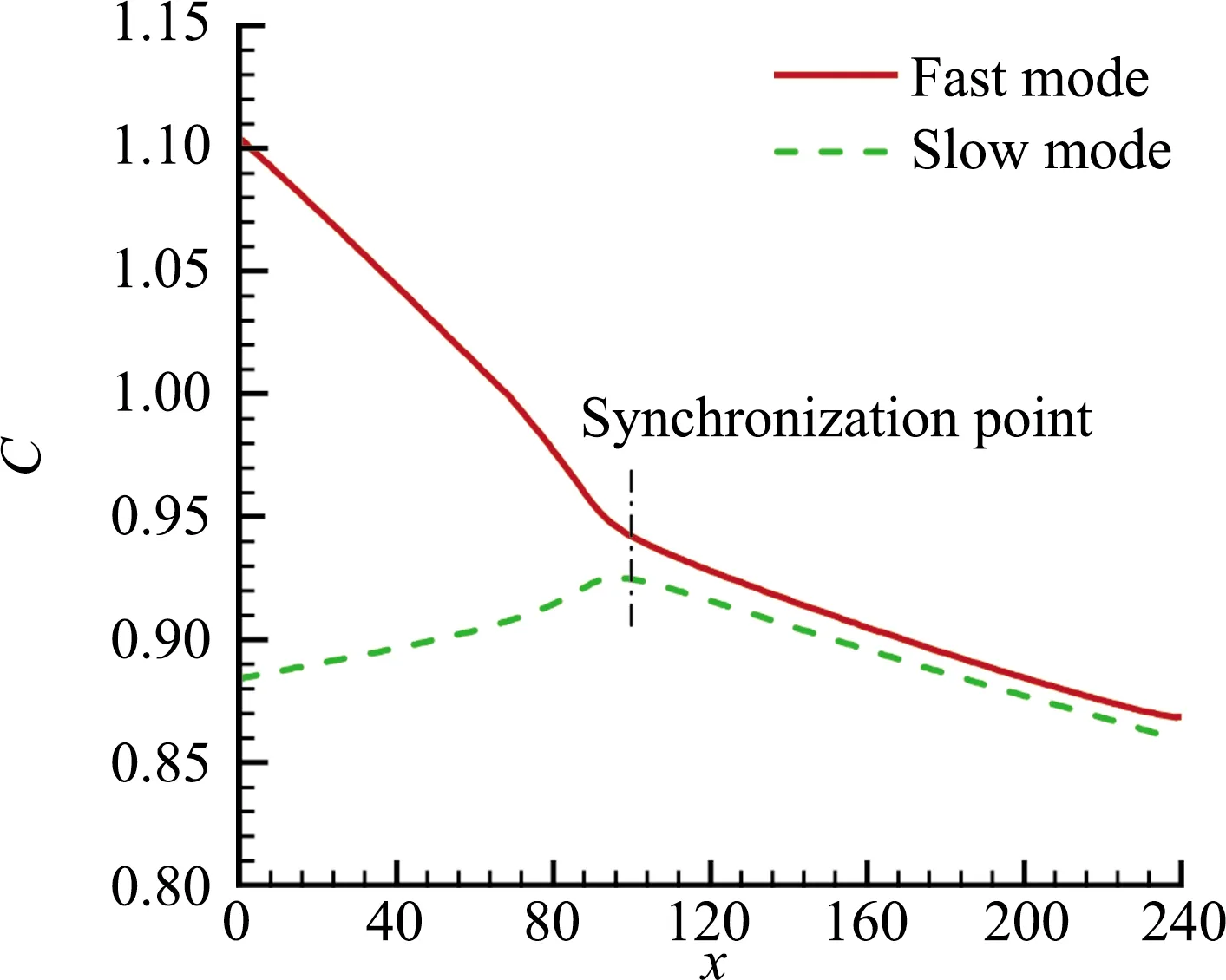
选取壁面温度为140 K，扰动频率为1，图1(a)、图1(b)中分别给出了LST分析得到的边界层内快、慢模态的相速度和增长率沿流向的变化。可见，该工况下，快、慢模态的相速度并没有严格的相交点，快模态与第二模态在x=100左右相速度最为接近，可认为是同步点。事实上，从图1(b)可知，该位置与扰动开始放大的中性点非常接近。快模态在下游的演化过程中始终是衰减的，而慢模态，即Mack第一模态，其相速度和增长率曲线在下游与增长的第二模态相连。

(a)相速度

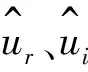
图2 入口处快模态的特征函数

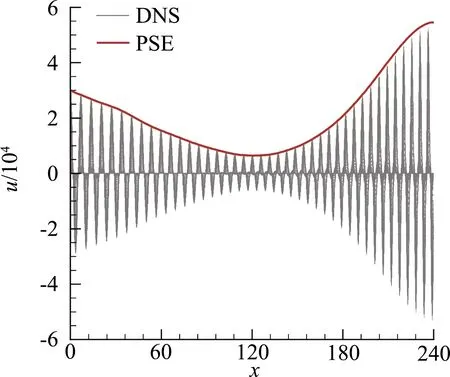
图3 快模态向下游的演化

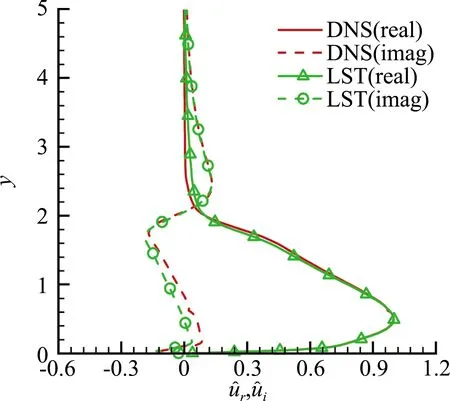
(a)x=165

3 考虑模态转换的扰动幅值计算方法

基于线性稳定性理论(LST)的eN方法，通过累计扰动的增长率来计算扰动的演化，即:

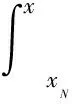
(5)

-αi表示扰动的增长率，xN表示中性点的位置，An表示中性点处扰动的初始幅值。由于线性稳定性理论忽略了非平行性，而在模态转换区域，非平行性的影响不再是可以忽略的高阶量[13]，因此，基于线性稳定性理论的eN方法无法从快模态开始，描述扰动向下游第二模态的转换过程。而PSE方法实质上求解的是一个演化问题，而非特征值问题，在实际的应用过程中远不如LST方便[26]。并且，若扩展到三维问题，可能需要采用面推进的方法，计算量很大，无法被工程实际采用[27]。为此，我们仍以LST为基础，发展可以考虑模态转换过程的扰动幅值计算方法。

考虑模态转换对第二模态波演化的影响应包含两个方面。一是，考虑模态转换发生的区间。模态转换发生在一定的流向区间内，转换完成后第二模态波才开始放大；二是，考虑第二模态开始放大的初始幅值。由于模态转换发生前，快模态经历一个衰减的过程，不同频率的快模态衰减的程度不同，因此，不同频率的第二模态开始放大的初始幅值也不同。因此，考虑模态转换过程的扰动幅值计算方法可写为:

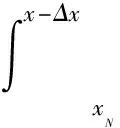
(6)

其中，A0表示某一位置x0处快模态的初始幅值，xN为中性点的位置，Γ为模态转换系数，表示在中性点处通过模态转换生成的第二模态的幅值与入口快模态的幅值之比，其大小与频率有关。由于模态转换并非准确地在中性点处完成，模态转换系数中生成的第二模态的幅值实质上是一种等效幅值。Δx代表模态转换区间，也与频率有关。假设在x0处激发的不同频率的快模态具有相同的初始幅值，取A0=3×10-4。本文仅考虑从快模态开始的演化过程，并不包含其激发过程。若能通过感受性研究估计出快模态扰动幅值与频率的关系，只要将式(6)中的A0替换为A0(w)即可。

根据PSE方法得到的扰动速度幅值的演化结果，以及采用LST从中性点处积分第二模态增长率的结果，如图5所示，可计算Γ和Δx。具体步骤为：1)根据PSE得到的幅值最大值Amax，计算对应的LST在中性点处的幅值，即An=Amax/eN,N为LST从中性点开始积分扰动增长率得到的最大N值，由式(5)给出；2)计算模态转换系数Γ，Γ=An/A0；3)由于LST没有考虑模态转换的过程，给出的第二模态增长比PSE的结果靠前，将其整体向下游平移Δx，两者结果一致，Δx即为模态转换区间。经过2)和3)两步得到的结果，也就是利用Γ、Δx采用式(6)得到的第二模态增长的结果，如图5中虚线所示。

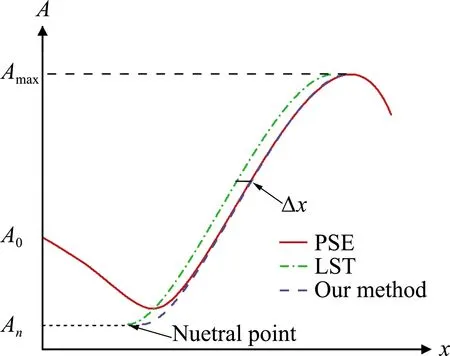
图5 模态转换系数Γ和模态转换区间Δx的示意图

分别考虑壁面温度为140 K、160 K、180 K和200 K的情况，采用LST得到的中性曲线如图6所示。由于低频扰动相对高频扰动而言具有更大的增长区域，我们主要考察频率较低的快模态。显然，快模态在模态转换前经历一个显著的衰减过程，由于我们主要的关注点是靠近中性曲线下支界区域的模态转换过程，为了减小计算量，将计算域入口移至x=500处。在该处引入快模态扰动，分别采用PSE方法计算不同频率的快模态向下游的演化，以及式(5)计算相应频率的第二模态波在不稳定区域内的增长，按照上述方法得到模态转换系数和转换区间，结果如图7和图8所示。图7中竖线标出了各壁面温度下对应的中性频率(中性点对应的频率)。由于实际中，快模态总是在不稳定区上游被激发，因此，我们只考虑频率小于中性频率的快模态。由图7可见，不同壁面温度下的模态转换系数随频率的变化具有相似的规律，即随着频率增加，模态转换效率增大，直至某一频率(略小于中性频率)。这是因为，频率越高的扰动，入口的位置距离中性点越近，快模态的衰减过程越短，从而对应的转换效率越高。而对于非常接近中性频率的扰动而言，模态转换需要在一定区域内完成，反而占据了一部分不稳定区域，因而降低了转换效率。图8给出的结果表明，模态转换需要的流向距离随着频率的增加而减小。

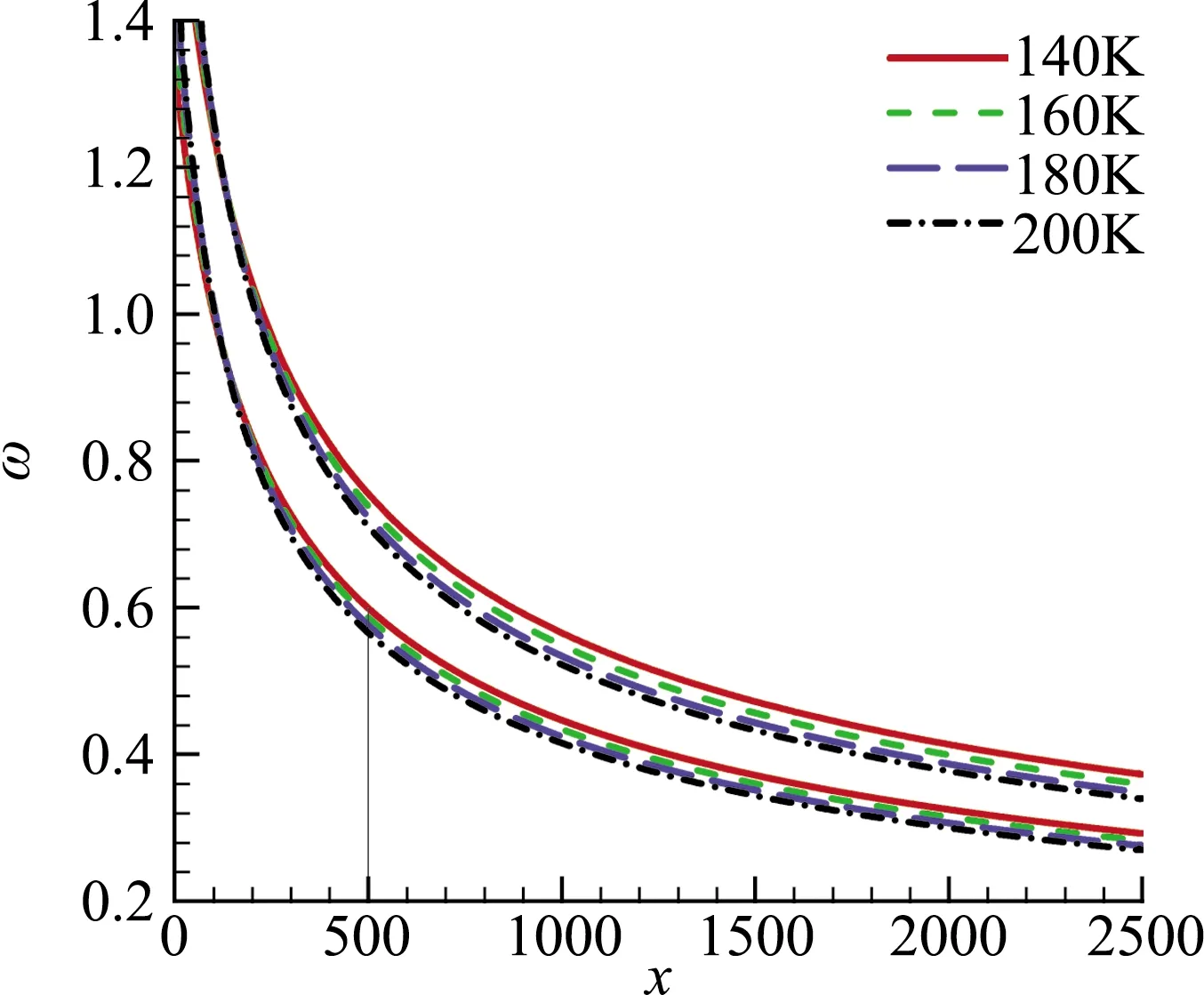
图6 不同壁面温度条件下的中性曲线

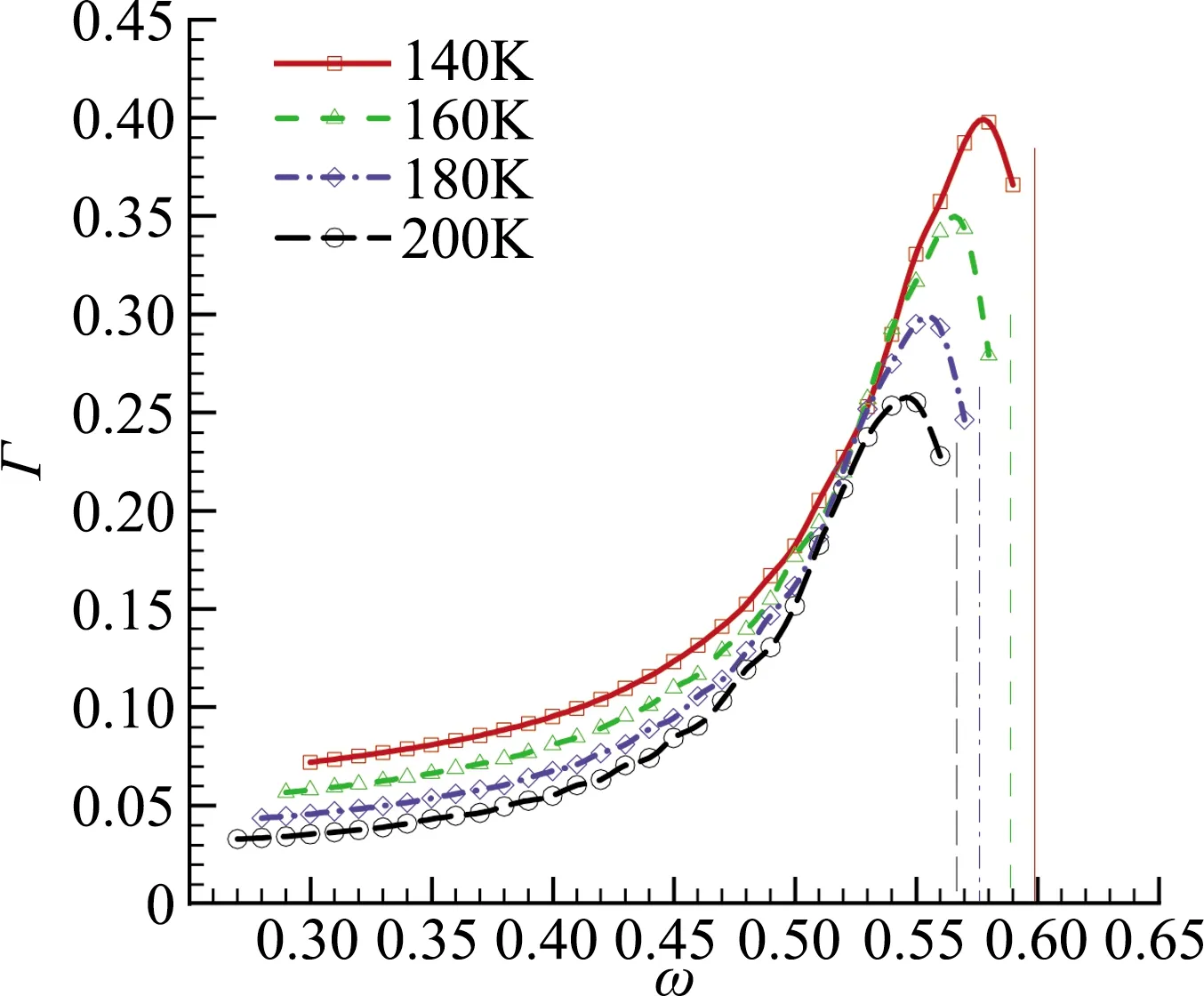
图7 模态转换系数Γ随频率ω的变化

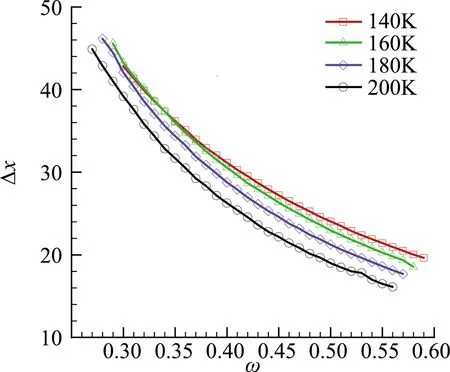
图8 模态转换区间Δx随频率ω的变化

可以发现，不同壁面温度条件下，图7给出的曲线具有相似的性质。为了在计算扰动演化时考虑模态转换的影响，需要建立Γ-ω的关系。考虑以下变换:

ω*=ωn-ω

(7)

ωn为中性频率，Δω代表了扰动波的频率范围，即ωn-Δω为考察的最低频率。本例中取Δω=0.3。Γm是Γ-ω曲线的峰值。假定Γm，Γ|ωn-Δω随壁面温度Tw变化是线性关系，利用图7中Tw=140 K和Tw=200 K的结果，可得:

Γm=-0.1492Tw/T∞+0.7144

Γ|ωn-Δω=-0.0424Tw/T∞+0.1622

(8)

在本文的计算中，ωn通过对基本流场进行稳定性分析得到。在实际应用中，简单起见，也可利用已知的两个壁面温度下的中性频率做线性插值得到。对于本文的算例，结果差别很小，未在此列出。采用PSE和LST计算更多壁面温度的Γ*-ω*曲线，所得结果如图9所示。可以发现，对于很广泛的壁面温度范围，Γ*-ω*曲线几乎是重合的。可以利用数据拟合的办法，建立Γ*-ω*的关系，即:

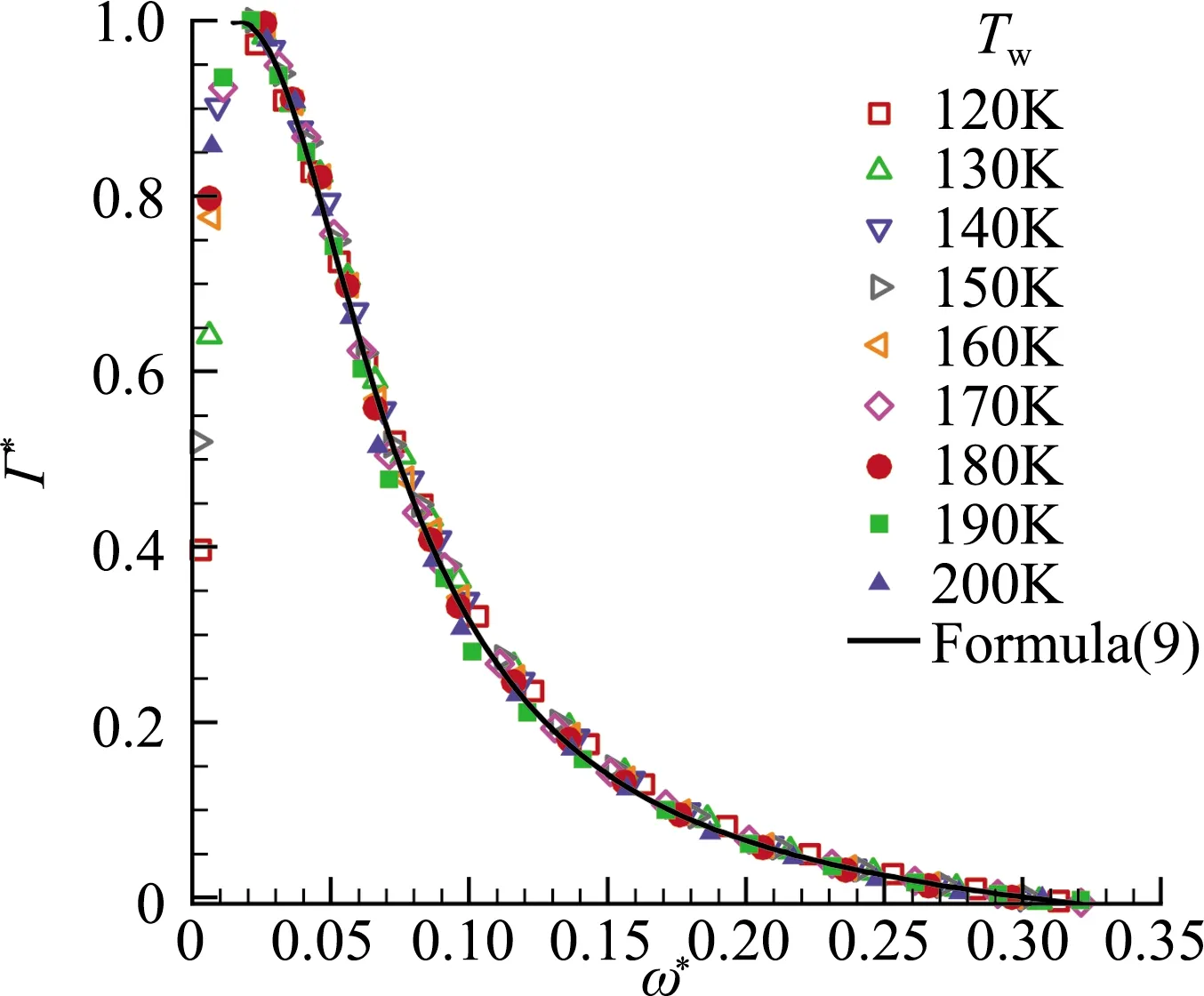
图9 不同壁面温度条件下的Γ*-ω*曲线

Γ*=1/(C1ω*2+C2ω*+C3)+C4ω*

(9)

其中，C1=296.7722，C2=-10.2683，C3=1.0874，C4=-0.1319。这样，根据式(9)，结合式(7)～(8)可计算给定壁面温度条件下的模态转换系数。

类似地，由图8给出的Tw=140 K和Tw=200 K的数据，可建立模态转换区间Δx与频率和壁面温度的关系，即:

Δx=-6.248Tw/T∞+14.8/ω+8.56

(10)

Fedorov等人[13-14]采用多尺度法研究模态转换时发现，模态转换区间Δx满足:

Δx=Cε2/3

(11)

其中，ε=1/ReLn，ReLn表示以中性点距平板前缘的距离Ln定义的雷诺数，C为常数。由于不同壁面温度下不同频率对应的中性点位置不同，因此ReLn与频率有关，即得到的Δx是频率的函数。在应用式(11)时，需要针对每个壁面温度条件，采用PSE方法计算某一个频率下的Δx，利用式(11)确定常数C。表1中给出了不同壁面温度下C的取值。图10给出了分别由式(10)和(11)计算的Δx与图8给出的数值结果的比较。可见，相比于扰动线性增长的区域(本例中为几百到几千个无量纲长度)，这两种方法计算出的Δx的差别很小。

表1 不同壁面温度下C的取值

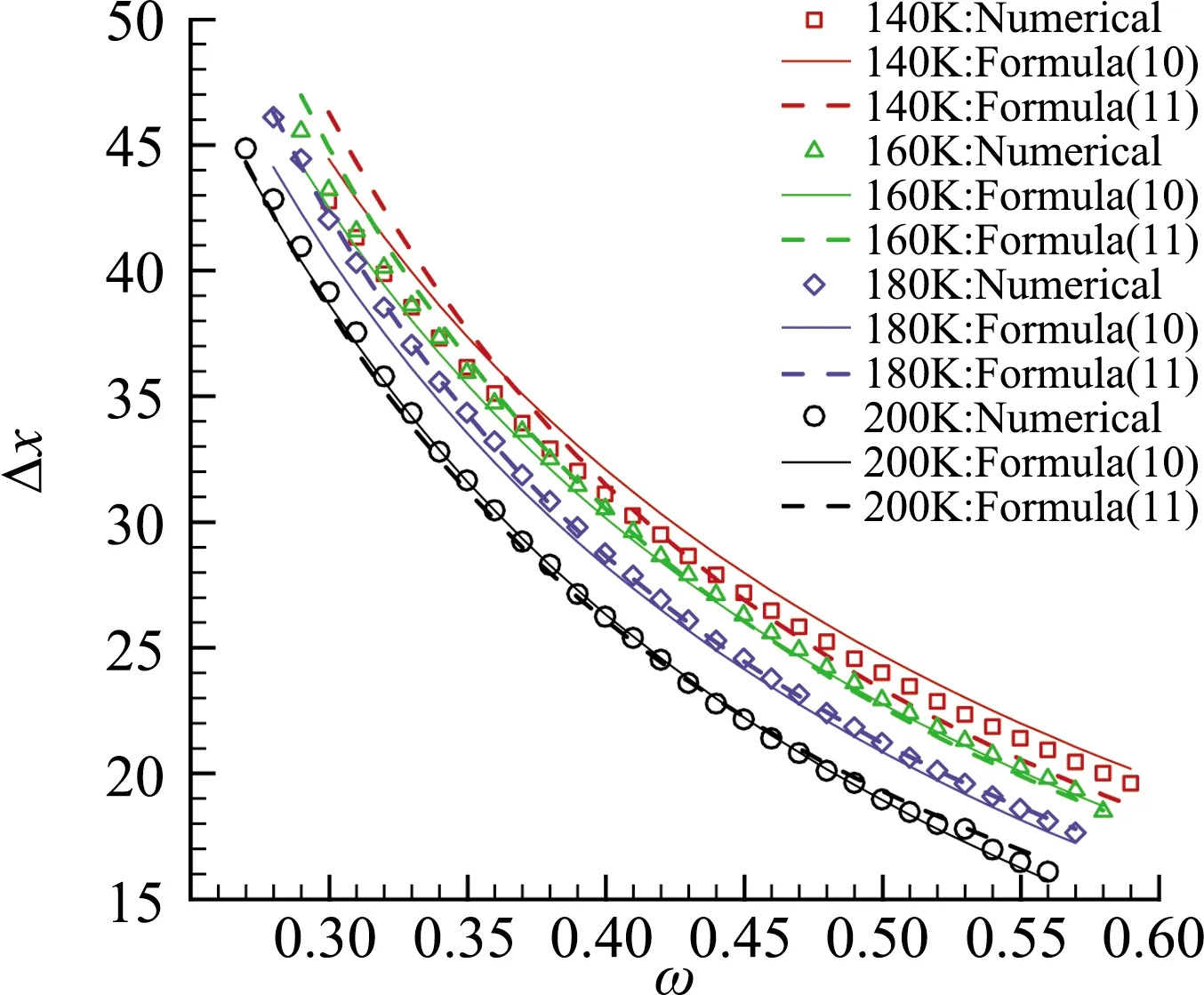
图10 不同方法计算的Δx随频率的变化曲线

4 扰动幅值计算方法的验证

考虑模态转换过程的扰动幅值计算方法可以描述为：给定壁面温度Tw，利用式(7)～(9)计算不同频率快模态的模态转换系数Γ，再结合式(10)或(11)给出的Δx，代入到式(6)中，计算由模态转换激发的不同频率的第二模态波的幅值演化。为了验证该方法的有效性，采用PSE计算快模态的演化进行比较。图11给出了壁面温度为150 K时，分别采用式(10)和式(11)计算得到的幅值演化曲线与PSE所得结果的比较。可见，考虑模态转换的扰动计算方法可以得到与PSE方法一致的结果。并且，分别采用我们建立的经验公式(10)与Fedorov给出的式(11)得到的模态转换区间，所得的幅值演化结果几乎没有差别。类似地，图12和图13分别给出了壁面温度为170 K和190 K的幅值演化结果。同样，考虑模态转换后的扰动演化结果与PSE的结果吻合很好。因此，采用该方法计算扰动的演化，结合一定的转捩判据，可以预测从快模态开始的包含模态转换过程的边界层转捩位置。

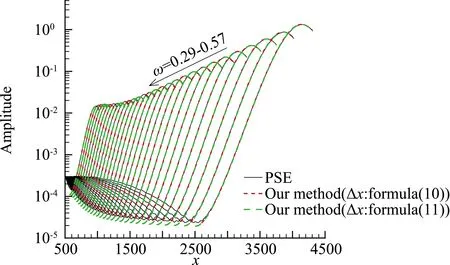
图11 扰动幅值演化结果(Tw=150 K)

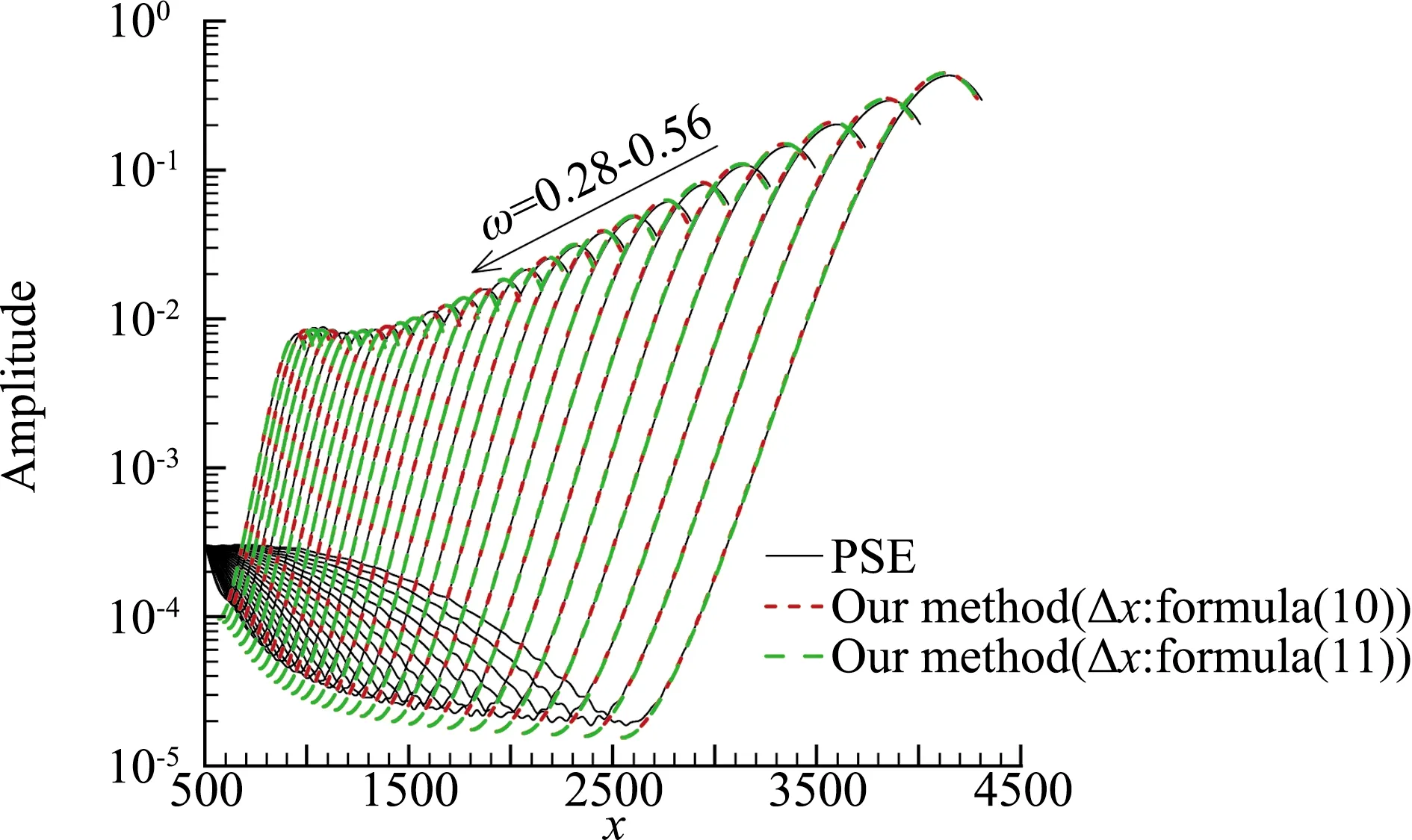
图12 扰动幅值演化结果(Tw=170 K)

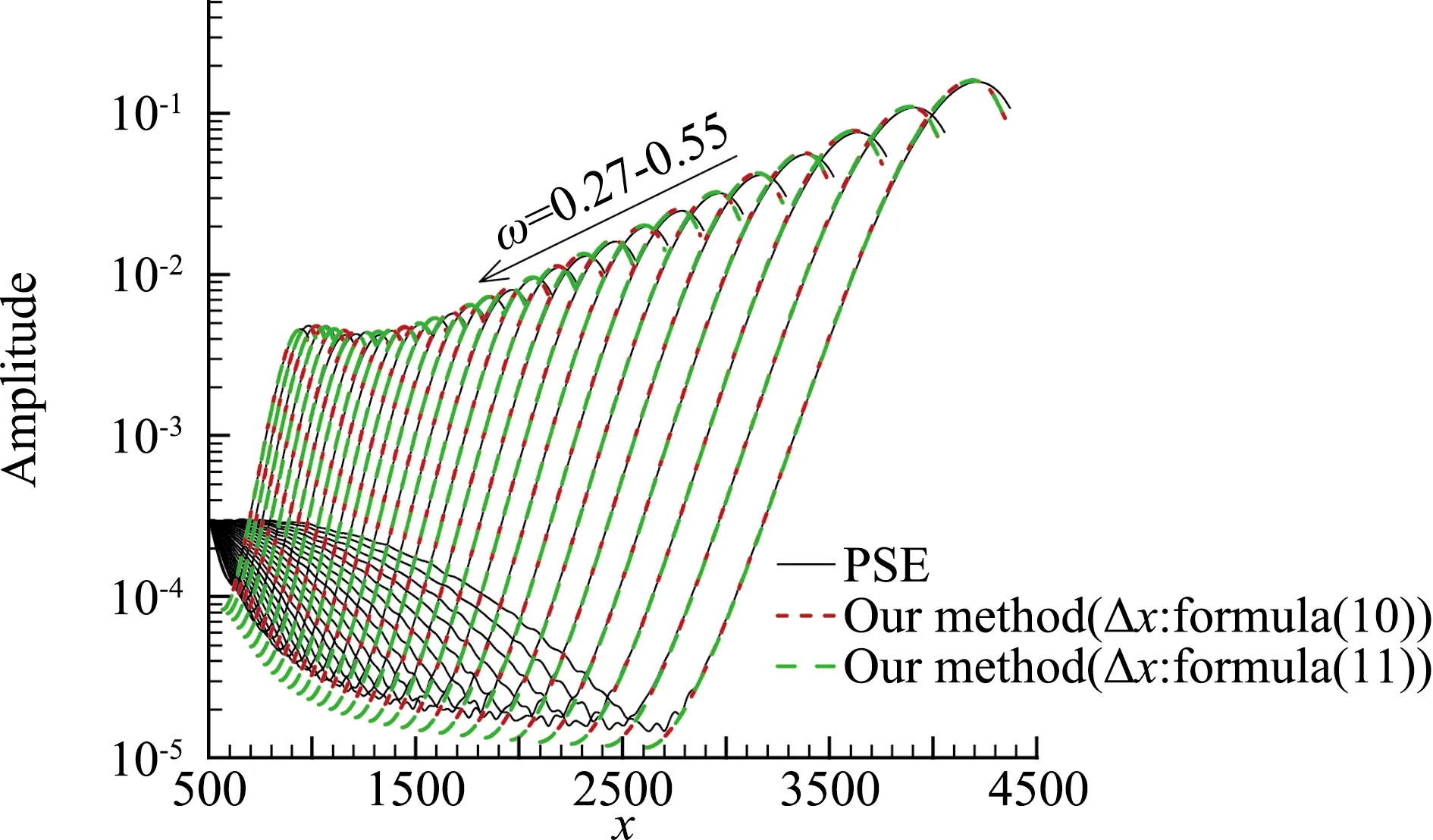
图13 扰动幅值演化结果(Tw=190 K)

5 结 论

本文采用直接数值模拟和抛物化稳定性方程的方法，对马赫数4.5的超声速平板边界层中快模态到第二模态的模态转换过程开展了研究。研究表明，PSE方法可以得到与DNS一致的扰动演化结果。利用PSE所得的结果，定义了模态转换系数和区间。研究发现，不同壁面温度下，模态转换系数、转换区间与扰动频率的依赖关系存在相似的规律。在此基础上，建立了考虑壁面温度条件的模态转换系数和转换区间的计算模型，发展了考虑模态转换的扰动幅值计算方法，并采用PSE对新发展的方法进行了验证。结果表明该方法可以在较广泛的壁面温度范围内，准确地描述从快模态到第二模态转换的扰动演化过程。

致谢:感谢天津大学吴雪松教授，多次与他进行的关于感受性问题的讨论给予作者很多启发性的思考。感谢天津大学韩宇峰博士在论文研究过程中给予的热情帮助。